Volumen del cilindro
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:06Volumen del cilindro
Aprendizaje esperado: calcula el volumen de prismas y cilindros.
Énfasis: resolver problemas que impliquen el cálculo del volumen del cilindro.
¿Qué vamos a aprender?
Estudiarás sobre un personaje muy famoso en la geometría: el cilindro recto. Para ello, profundizarás en la resolución de problemas que impliquen el cálculo del volumen de estos cuerpos geométricos.
¿Qué hacemos?
Reflexiona en las siguientes preguntas, anótalas y contéstalas conforme avances en la sesión:
- ¿Qué características tienen los cilindros y qué diferencia tienen con los prismas rectos, cuya base es un polígono regular?
- ¿Por qué es importante comprender y dar sentido, y significado, al volumen de un cilindro cualquiera?
- ¿Cómo piensas que se calcula el volumen de cualquier cilindro?
- ¿Qué relación identificas entre los prismas rectos cuya base son polígonos regulares y los cilindros?
Seguramente ya tienes muchas ideas y argumentos para responder, y otras preguntas que tienes acerca de los cuerpos geométricos, específicamente de los cilindros y prismas rectos, cuya base es un polígono regular.
A continuación, analiza la siguiente situación.
Situación-problema 1. Cubos de plastilina
Berna le regaló a su nieta Guadalupe un juego de cubos de plastilina de colores con algunos accesorios para cortarlas, y le pidió que elaborara diferentes cuerpos geométricos.
Guadalupe formó con los cubos de plastilina el bloque 1 que se muestra. Obsérvalo con detalle.

¿Qué características identificas en el bloque 1?
¿Qué figuras geométricas conoces?
Luego, con la pieza circular de color amarillo, Guadalupe cortó el bloque 1 y obtuvo el bloque 2 que se muestra.

¿Qué características identificas en el bloque 2?
¿Qué figuras geométricas conoces?
¿Sabes cómo se llama el cuerpo geométrico que es semejante a la forma del bloque 2?
La figura del bloque 2, se llama cilindro, y seguramente has visto cuerpos geométricos con sus mismas características, más de una vez.
De acuerdo con el problema anterior, considera como unidad cúbica cada cubo de plastilina.

Con esta consideración responde la siguiente pregunta:
¿Cuál es el volumen o cuántas unidades cúbicas forman el bloque 1, que ha construido Guadalupe?
El bloque 1 tiene seis unidades cúbicas por lado, y dado que su forma es cuadrangular, se puede multiplicar 6 x 6 para conocer el total de unidades cúbicas, que es igual a 36. También puedes contarlas una a una. Ésta es una manera de calcular su volumen.
Pero, también se sabe que todas las aristas de cada unidad cúbica o cubo de plastilina miden 2.5 cm por lado, considerando esta medida:
¿Cuál es el volumen del bloque de plastilina?
¿Cómo puedes calcular el volumen del bloque de plastilina?
Analiza la situación. Dadas las características de un cubo, las medidas de sus lados son iguales, tanto su largo, ancho y alto miden 2.5 cm.
Con esta información, continúa con el análisis del bloque 1, el cual tiene tres dimensiones:
Su alto es igual a 2.5 cm. Su largo mide 15 cm, ya que son 6 unidades cúbicas que lo forman:
2.5 x 6 = 15
Asimismo, su ancho es igual a 15 cm. Por lo tanto:
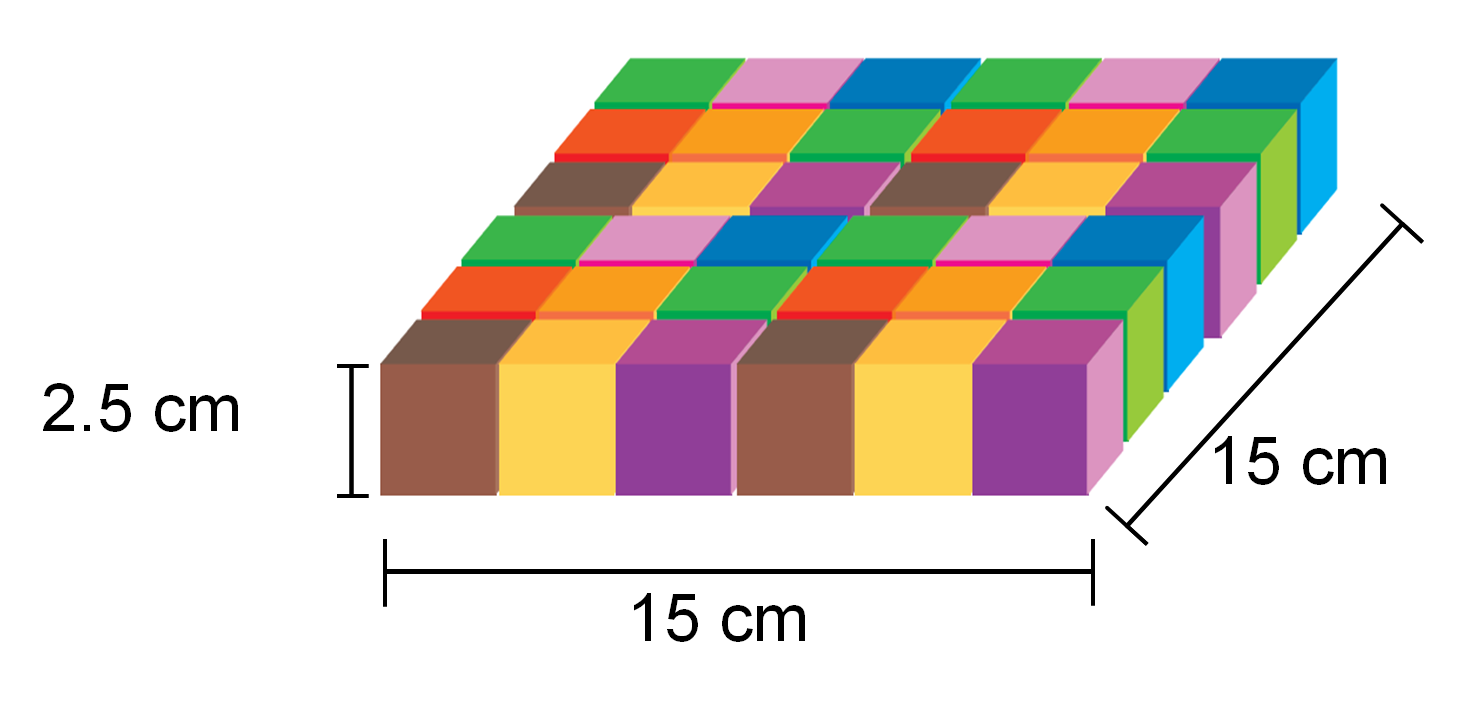
El volumen de un cuerpo se obtiene al multiplicar la medida del largo, por el ancho y por la altura. De esta manera se tiene que el volumen del bloque 1 es igual a:
15 x 15 x 2.5 = 562.5
Por lo tanto, el volumen del bloque 1 es igual a 562.5 cm cúbicos.
Otra forma de calcularlo es multiplicar el volumen de cada cubo de plastilina:
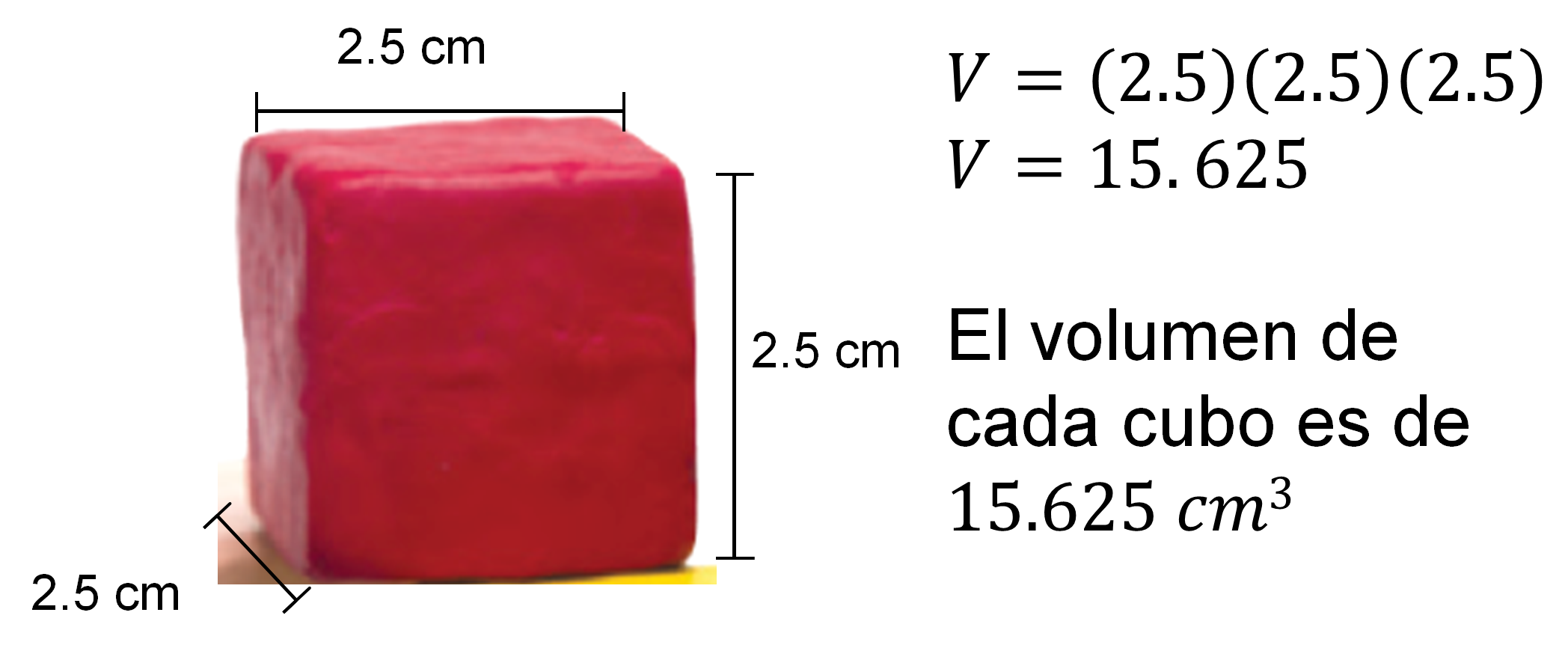
El volumen de cada cubo es de 15.625 cm cúbicos.
Ahora sabes que cada cubo tiene 15.625 cm cúbicos de volumen. Con este dato, multiplica el total de unidades cúbicas que forman el bloque 1, que son 36, por 15.625, que es igual a 562.5 cm cúbicos.
El bloque 1 tiene un volumen de 562.5 cm cúbicos. Con ambos métodos se obtuvo la misma medida del volumen.
Es momento de analizar el segundo cuerpo geométrico que construyó Guadalupe, que se llama cilindro.
Aproximadamente, ¿cuántas unidades cúbicas forman el cilindro?
Para hacer una buena estimación; en la vista superior del cilindro traza un cuadrado dentro, y observarás que está formado por 16 unidades cúbicas.
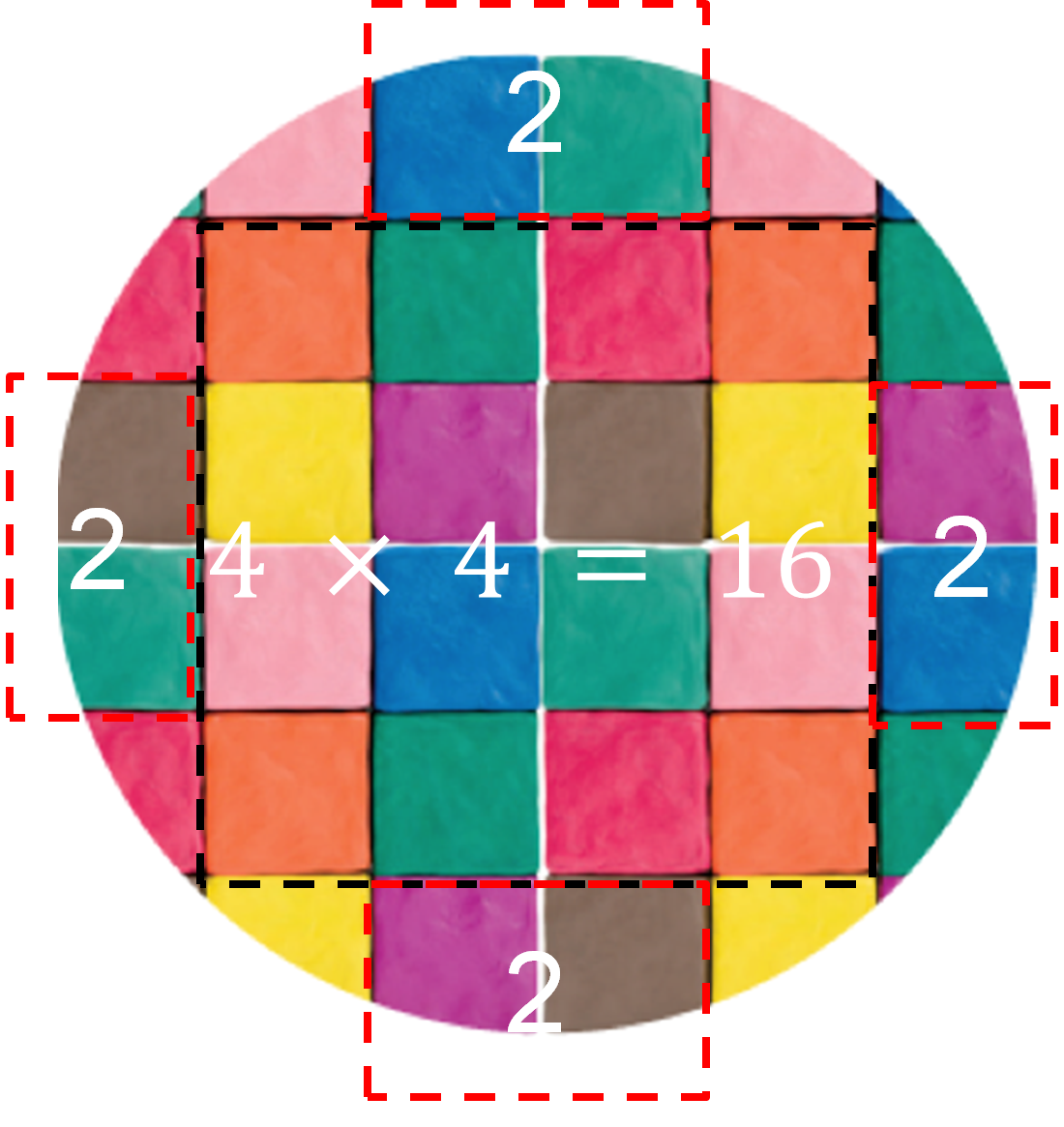
Luego, considera la parte que fue cortada por la pieza circular y realiza “compensaciones” entre los cubos de plastilina, de esta manera, sumarás 8 cubos más que corresponden a los cubos de los lados del cuadrado.
Finalmente, considera como 1 a cada par de cubos amarillos y rosas al compensarlos, por lo que se suman 2 cubos más.
El cilindro tiene aproximadamente 26 unidades cúbicas. Considerando estos datos:
¿Cuál es su volumen?
El volumen de un cubo de plastilina es igual a 15.625 cm cúbicos. Por lo tanto, se puede multiplicar el total aproximado de cubos de plastilina, que son 26 por 15.625, que es igual a 406.25 cm cúbicos.
Ahora, analiza lo siguiente:
Guadalupe hizo otro bloque de plastilina, lo cortó con su pieza amarilla y ahora tiene un cilindro de dos cubos de alto, como se muestra en la imagen.
¿Cuántas unidades cúbicas forman el nuevo cilindro?

Si se analizan por separado, los cilindros son iguales o congruentes, por lo tanto, el total son 52 unidades cúbicas aproximadamente. Y su volumen es el doble, es decir 406.25 x 2 que es igual a 812.5 cm cúbicos.
Guadalupe continuó haciendo bloques de plastilina y a su vez, los cortó con la pieza circular, hasta tener un cilindro con cinco cubos de alto, como se muestra en la imagen.
¿Cuántas unidades cúbicas forman este otro cilindro?
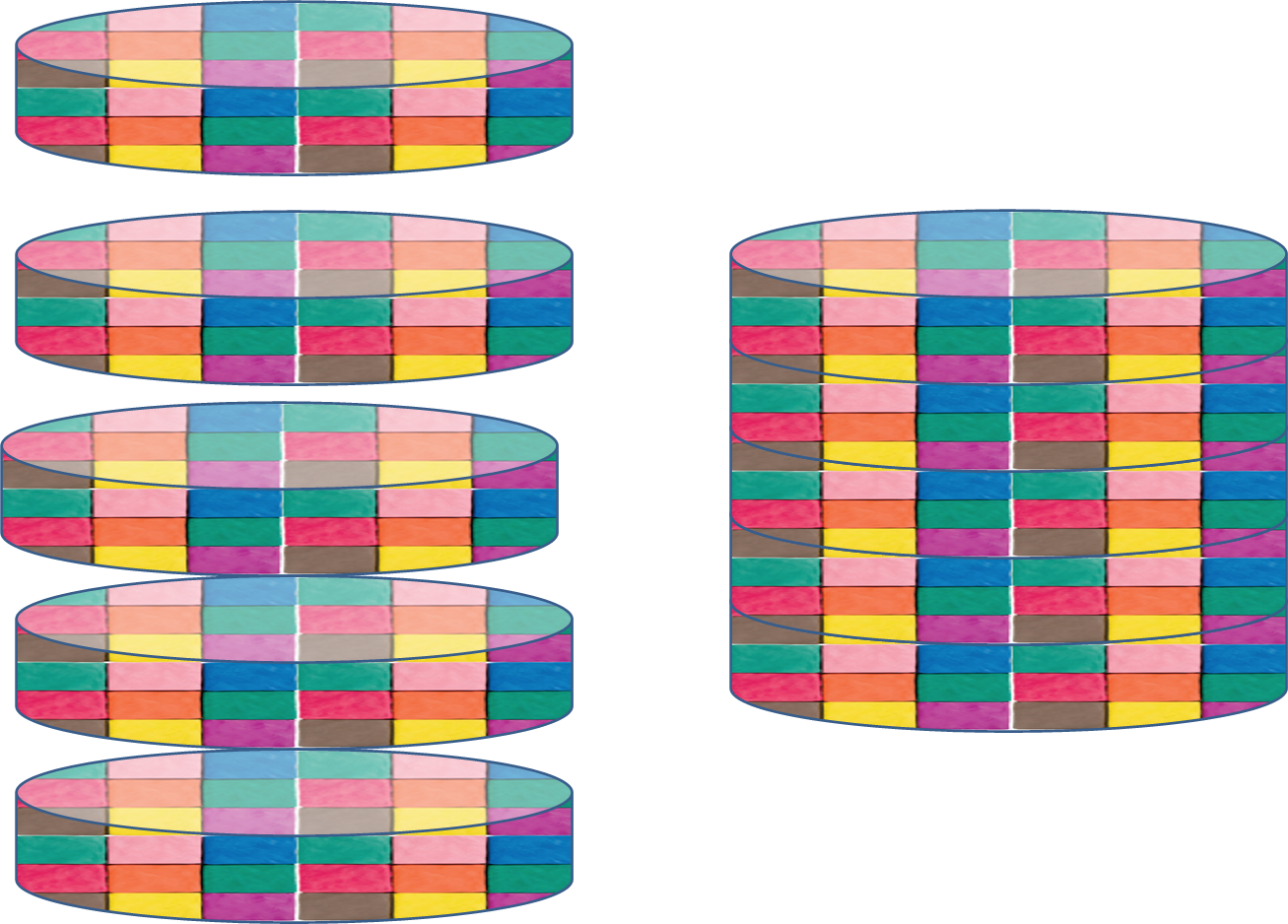
Considerando los procedimientos anteriores, multiplica 406.25 cm cúbicos por 5, que es igual a: 2031.25 cm cúbicos.
También puedes aplicar el siguiente procedimiento: 130 unidades cúbicas o cubos de plastilina por 15.625, es igual a 2031.25 cm cúbicos.
Reflexiona en lo siguiente:
¿Habrá otra manera de calcular el volumen del cilindro?
¿Habrá alguna relación entre el método para calcular el volumen del cilindro con el método para obtener el volumen de prismas poligonales?
Registra tus razonamientos y conjeturas, ya que las podrás validar o refutar conforme vayas profundizando en el tema de estudio.
El volumen de prismas poligonales se obtiene al calcular la medida del área de la base del prisma por la altura.
¿Cómo puedes obtener el área de la cara circular del cilindro?
Observa los bloques de plastilina y las siguientes imágenes, analízalas e identifica, en qué son semejantes y en qué son diferentes.

Son similares, pues están conformados por cuerpos de forma circular. Al apilarse, su forma es semejante a la de un cilindro recto. En ese sentido tienen dos bases circulares.
Son diferentes en el tamaño de la base y en la altura, por ejemplo, en las columnas de las monedas.
Ahora, observa los cuerpos geométricos. Un cilindro recto y un prisma cuya base es un polígono de 10 lados. Son diferentes en la forma de la base.
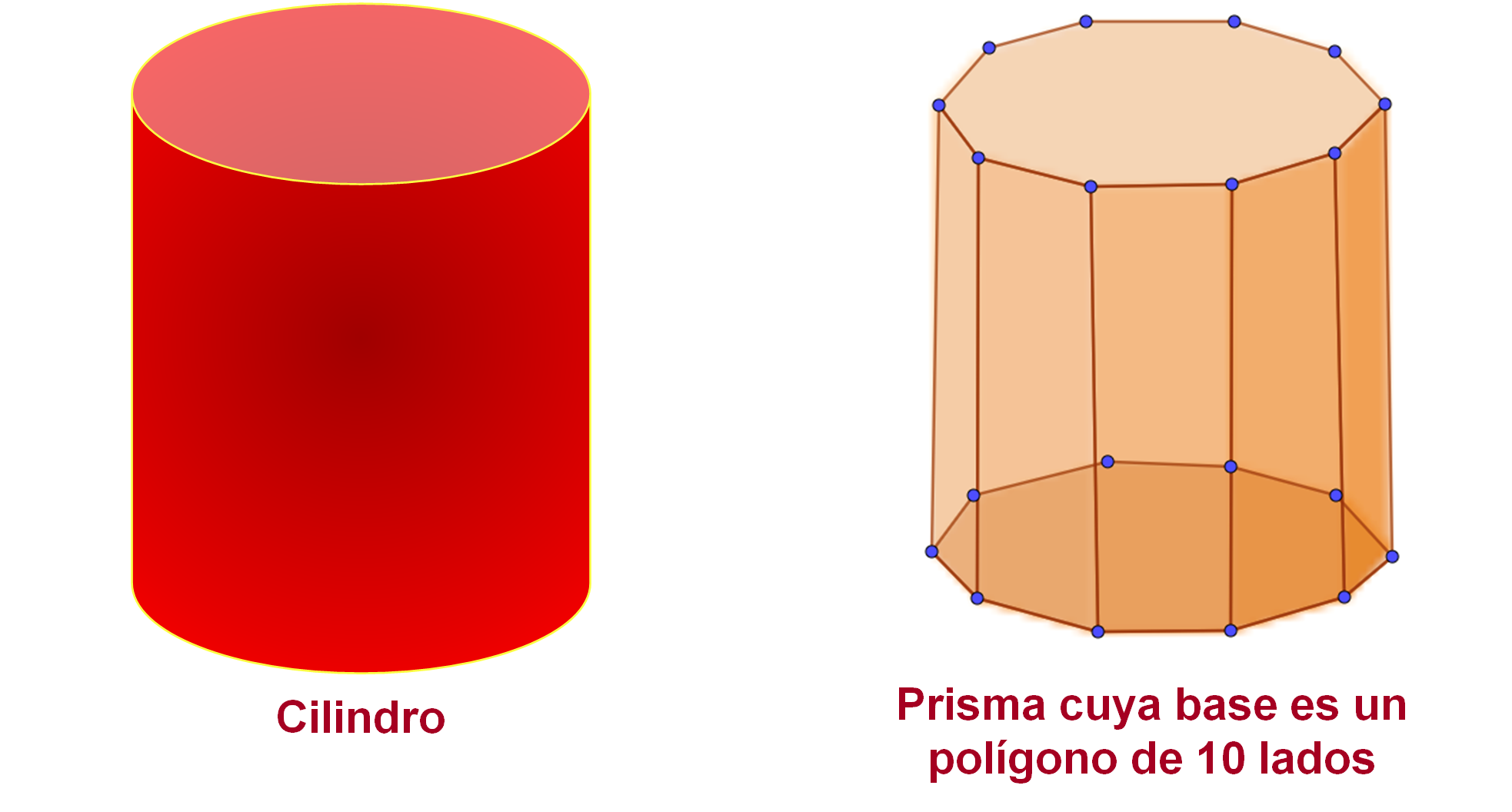
Retoma la pregunta:
¿Habrá alguna relación entre el método para calcular el volumen del cilindro con el método para obtener el volumen de prismas poligonales?
Para conocer el área de un círculo, se utiliza la siguiente formula:
Área círculo = pi multiplicado por el radio al cuadrado.
Sabes que el bloque de forma rectangular de plastilina mide 15 cm de lado. También que el diámetro del círculo pasa por su centro y tiene sus puntos extremos en el círculo.
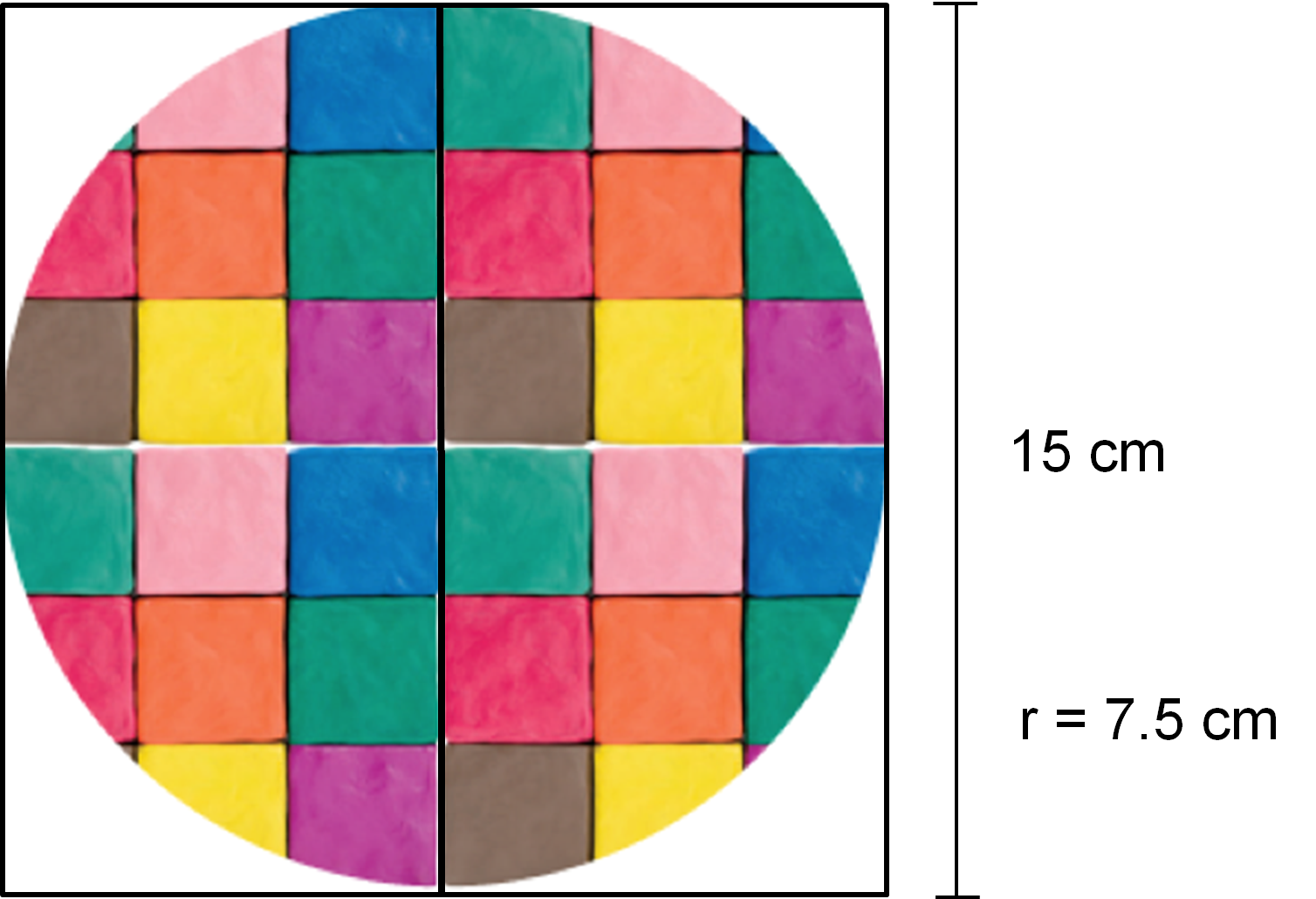
El diámetro de cualquier círculo es dos veces la longitud del radio del círculo. Por lo tanto, el radio del círculo es igual a 7.5 cm.
Con este dato, puedes calcular el área del círculo.
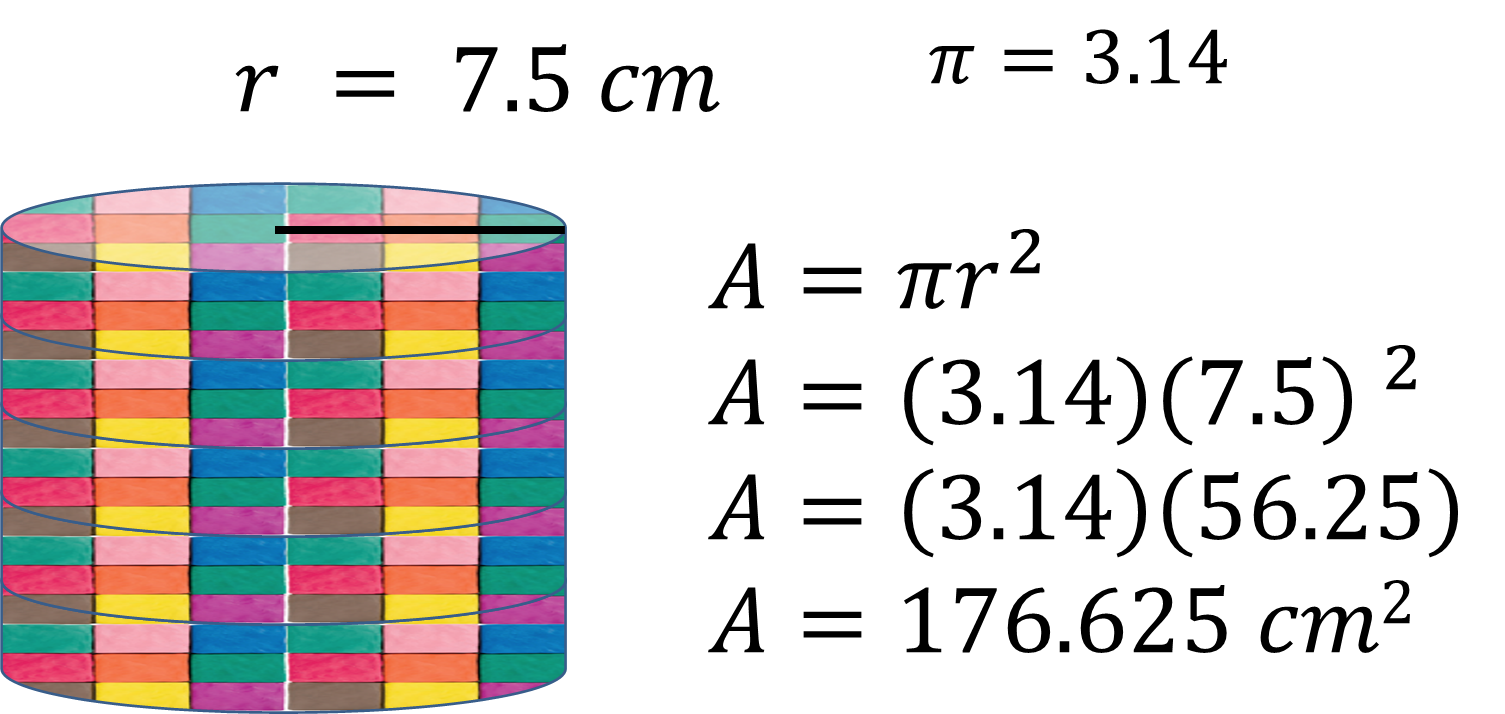
¿Qué otros datos tienes?
Su altura es de 12.5 cm.
¿Habrá alguna relación entre el método para calcular el volumen del cilindro con el método para obtener el volumen de prismas poligonales?
Observa: el volumen de los prismas poligonales es igual al área de la base por altura.
Continúa usando este método:
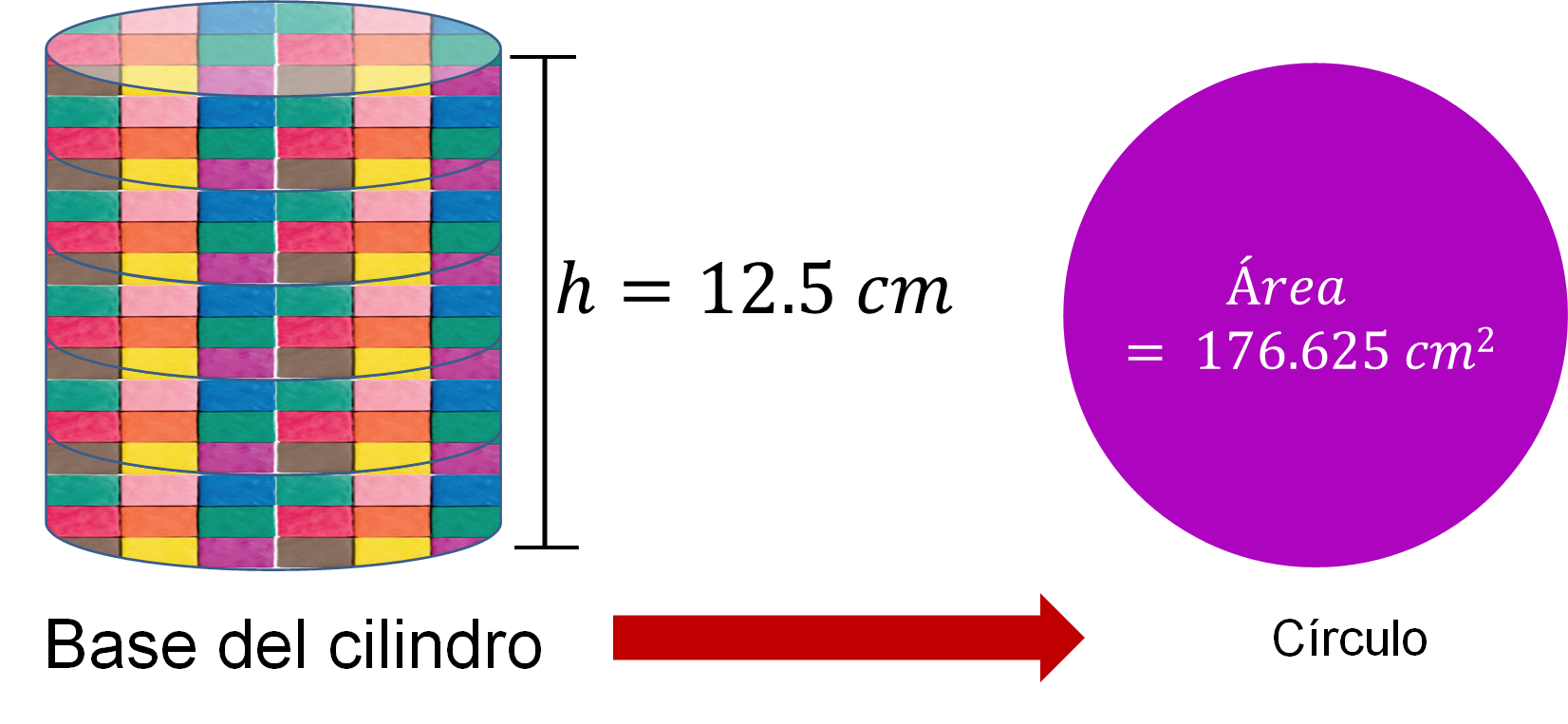
El área del círculo es igual a 176.625 cm cuadrados
El Volumen = 176.625 (12.5) = 2,207.8125 cm cúbicos
Entonces, el cilindro tiene de volumen 2,207.8125 cm cúbicos. Siguiendo el método para obtener el volumen de prismas poligonales has calculado el volumen del cilindro.
Al comparar el volumen del cilindro, el cual se obtuvo con el conteo estimado de los cubos de plastilina que forman la cara circular, identificaste que es igual a 2031.25 cm cúbicos.
Se obtuvieron resultados diferentes, pero dentro de un rango numérico razonable. Esto se debe al uso de procedimientos distintos. Cada uno es útil, dependiendo del contexto en el que se emplea. Si no tienes forma de obtener una medida, la estimación es una buena estrategia, pero si conoces las medidas, obtendrás cálculos más cercanos, o hasta donde el cálculo con los números decimales te lo permita.
A continuación, analiza la información del siguiente audiovisual con la finalidad de profundizar en la relación entre la fórmula del volumen del cilindro y los prismas rectos, cuya base es un polígono regular.
- Volumen de cilindros.
https://www.youtube.com/watch?v=V4Li3l-dgZg
Gracias al audiovisual aprendiste que hay una relación entre el método para obtener el volumen de prismas poligonales y el método correspondiente al cálculo del volumen del cilindro.
De esta manera sabes que el volumen de cualquier cilindro recto se obtiene al calcular el área de la base, en este caso siempre será un círculo, cuya fórmula es:

A continuación, analiza el siguiente planteamiento.
Problema. El pozo
Un pozo tiene un diámetro de 4 metros y una profundidad de 15 metros.
Al modelar el pozo con un cilindro recto, se sabe que éste 2 m de radio.
¿Cuál es el volumen del pozo?
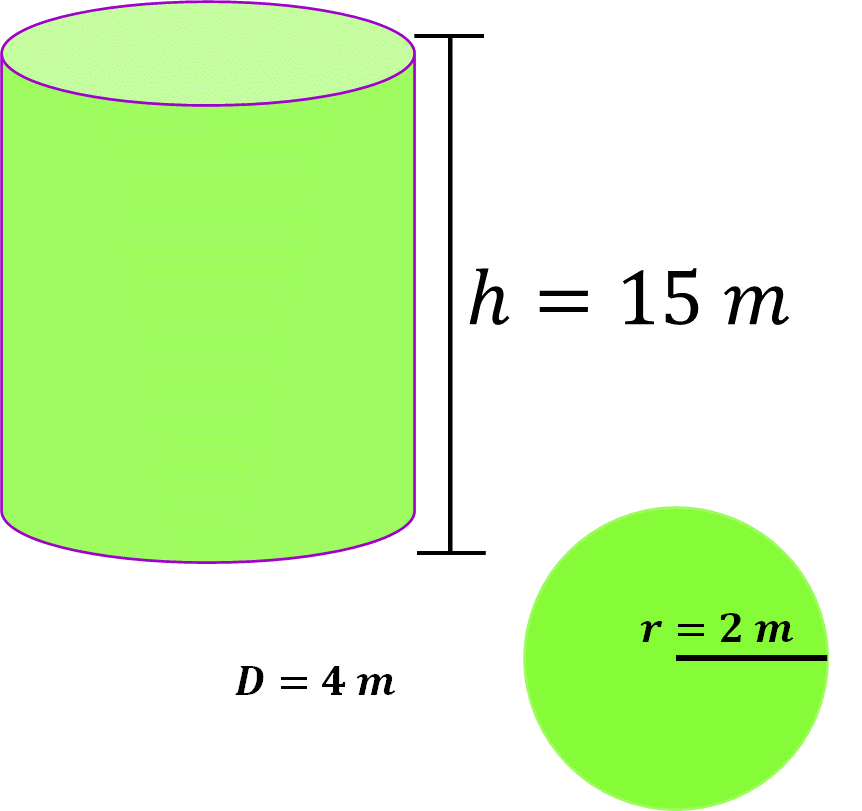
Para calcular su volumen, necesitas conocer la medida del área de la base. Aplica la fórmula, área es igual a pi por radio al cuadrado. Después, sustituye en la fórmula las medidas y resuelve las operaciones:

Por lo tanto, el área del círculo es igual a 12.56 metros cuadrados.
Para calcular el volumen, sustituye la medida obtenida previamente y resuelve las operaciones:
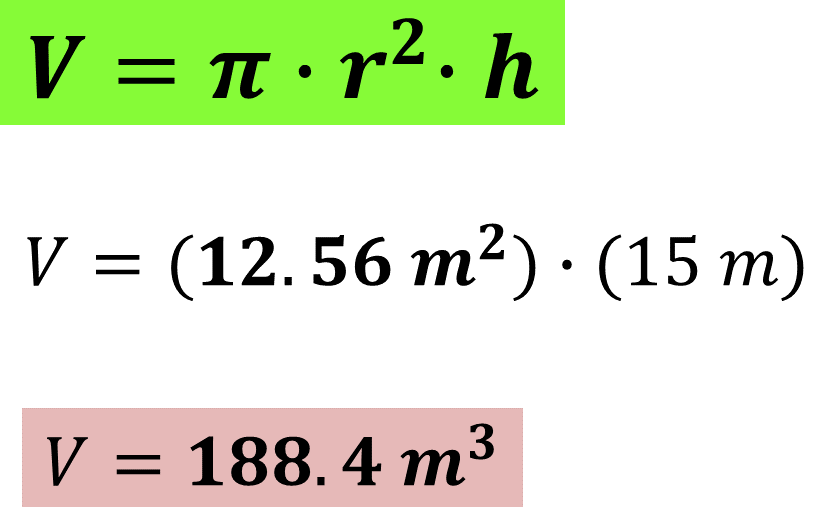
Ahora sabes que el volumen del cilindro es igual a 188.4 metros cúbicos.
Has profundizado en los prismas rectos de base poligonal y su relación con los cilindros, de estos últimos has calculado su volumen. Ahora, resuelve el siguiente ejercicio.
Problema. Cilindro sin radio
Observa el cilindro recto, cuyo volumen es de 310.86 cm cúbicos. Se conoce la medida de su altura, que es de 11 cm.
¿Cuál es la medida del radio?
¿Cómo puedes determinar el dato faltante?
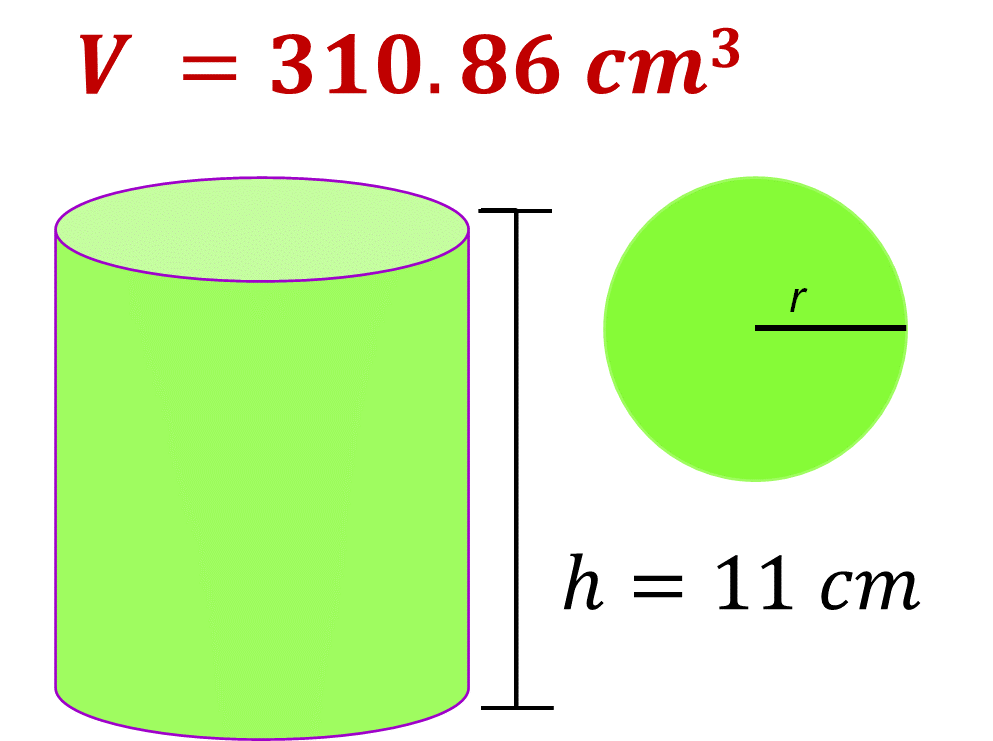
Para calcular el volumen del cilindro se emplea la fórmula:
V = Área de la Base por h
o
V = pi por radio al cuadrado por h
Los datos que tienes son tres medidas: el volumen, pi y la altura. Puedes usar la fórmula para determinar la medida del radio de la cara circular.
Sustituye los valores conocidos:

De esta manera, se determina la medida del radio.
Ahora, ¿cuál es la medida de la altura del cilindro, que mide 375 cm cúbicos de volumen? y de área de la base 25 cm cuadrados.
¿Cómo puedes determinarlo?
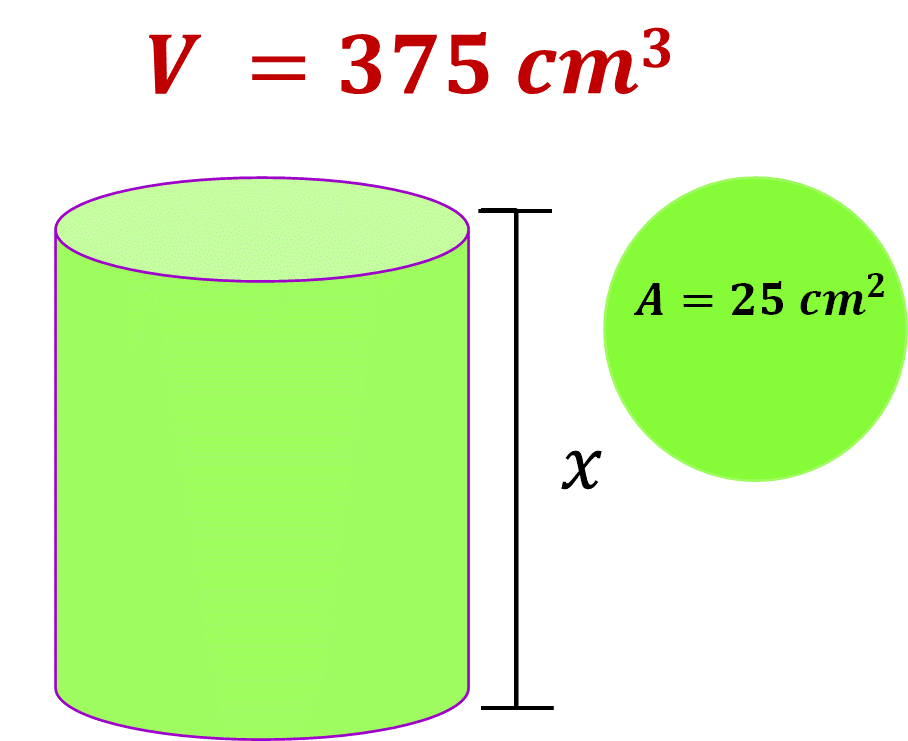
El volumen de un cuerpo geométrico se obtiene al multiplicar la medida de la altura por la medida del área de la base.
Conoces el volumen, que es de 375 centímetros cúbicos, y 25 cm cuadrados de área de la base. Necesitas encontrar la medida de su altura. Para ello divide 375 entre 25, cuyo cociente es 15, como lo que buscas es la medida de la altura, ésta mide 15 cm.

Esto se verifica al obtener el volumen: multiplica el área de la base por 15 cm de altura, y obtendrás 375 cm cúbicos de volumen.
Has concluido la sesión. Recuerda que este es un material de apoyo y puedes consultar otras fuentes para complementar lo que aprendas aquí.
El reto de hoy:
Registra tus reflexiones y elabora tus propias definiciones y características sobre los cilindros rectos y su volumen, y contrástalos con lo que se ha visto en la sesión.
Consulta tu libro de texto de Matemáticas de segundo grado, y resuelve las actividades que encuentres, éstas te ayudarán a profundizar en este tema.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion