Vamos a vencer retos

Vamos a vencer retos

Aprendizaje esperado: identifica una fracción o un decimal entre dos fracciones o decimales dados. Acercamiento a la propiedad de densidad de los racionales, en contraste con los números naturales.

Énfasis: estrategias para calcular decimales y fracciones dadas dos fracciones.

¿Qué vamos a aprender?

Vas a reafirmar lo aprendido en las sesiones pasada, seguirás aprendiendo sobre números decimales y fracciones.

¿Qué hacemos?

Enfrentarás algunos retos para demostrar que puedes vencerlos auxiliándote de lo que has aprendido. Es muy importante asumir retos porque al resolverlos te sientes satisfecho o satisfecha, o te obligas a pensar y buscar más para lograrlo.

Incia con el reto siguiente.

Luis y Ana salen con su perra “Pildorita” a correr todas las mañanas a una pista que hay cercana a su casa. Ana ha recorrido 52.2 m de la pista y Luis ya recorrió 52.1 m de la pista y su perro va entre ellos dos. Esta recta representa la ubicación de Ana y Luis. Señala algún punto donde pueda encontrarse la perra y la distancia que representa ese punto.

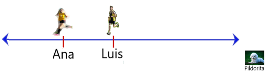
Si sólo ves los números parece que no se podría ubicar a Pildorita en medio de ellos dos, pero si observas la imagen, sí puede ir en medio.

Puedes darte cuenta que 52.1 metros y 52.2 metros, es como decir 52 metros con un decímetro y 52 metros con 2 decímetros. Y como ya sabes que cada decímetro tiene 10 centímetros, entonces puedes escribirlo también así.

52.1 m = 52 metros 10 centímetros.

52.2 m = 52 metros 20 centímetros.

Entonces. entre los 10 y 20 centímetros están 11, 12, 13, 14, 15, 16, 17, 18 y 19. Así que Pildorita puede estar en cualquiera de esos puntos.

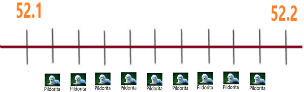
La diferencia entre la distancia de Luis y de Ana es de 1 decímetro, la cual equivale a 10 centímetros, Pildorita puede ir muy cerca de Ana o de Luis, a sólo a unos cuantos centímetros de distancia de cualquiera de ellos.

La siguiente imagen tiene un tronco sobre el cual se pararon dos mariposas, que andaban revoloteando alegres. Llegó una tercera mariposa y se paró sobre el tronco en medio de las dos anteriores, señalen en qué punto pudo haberse parado.

Observa como se puede identificar la ubicación de las mariposas.

Se identifica que 1.6 m es lo mismo que 1 metro con 6 decímetros y 1.7 m es lo mismo que 1 metro con 7 decímetros, y como cada decímetro tiene 10 centímetros, entonces es como escribir 1 metro 60 centímetros y un metro 70 centímetros, así se podían encontrar entre 60 y 70 varios números. Por lo tanto, la tercera mariposa se pudo haber parado sobre el tronco a una altura de 1.61, 1.62, 1.63, 1.64, 1.65, 1.66, 1.67, 1.68, 1.69 metros.

En cualquiera de esas distancias en el tronco pudo haberse parado esa tercera mariposa, muy cerca de las otras dos.

En un centro deportivo se hizo una competencia de natación infantil. Lucía, Patricia y Martha hicieron el tiempo que está anotado en esta tabla, pero el tiempo que hizo Martha se borró de la tabla, ¿Cuál pudo haber sido el tiempo marcado por ella?

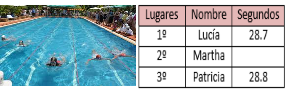
Es importante tener presente que después de los segundos el tiempo se divide en décimas de segundo. Así que, si Martha quedó en segundo lugar, después de Lucía que hizo 28 segundos con 7 décimos y antes de Patricia que hizo 28 segundos con 8 décimos, entonces era necesario que los décimos de segundo las dividiéramos en centésimos para ver cuál pudo ser el tiempo de Martha.

Martha pudo haber llegado en 28.71, 28.72, 28.73, 28.74, 28.75, 28.76, 28.77, 28.78 o 28.79 segundos.

Silvia, Roberto y Fernando se comieron gran parte de un pastel. Cuando su mamá los descubrió, preguntó cuánto pastel había comido cada uno y ellos le dieron esta respuesta.

Silvia dijo: yo me comí solamente un cuarto del pastel, Roberto dijo: yo comí 2 cuartos y Fernando dijo, yo comí una rebanada más chica que la de Silvia y un poco más grande que la de Roberto. ¿Cuánto pastel pudo haber comido Fernando? Fíjate bien que lo que comió Fernando, debe ser una cantidad que es mayor que 1 cuarto, pero menor que dos cuartos.

Entre un cuarto y dos cuartos, se pueden encontrar varios números.

Para encontrar un pedazo de pastel que fuera más grande que el de Silvia, pero más chico que el de Roberto, se tenía que buscar un número que estuviera entre 1 cuarto y 2 cuartos. Entonces se puede señalar en una recta numérica que representara el pastel. Primero se ubica un cuarto y dos cuartos, luego se identifica que entre ellos puede haber varios pedazos más, entonces se divide el pastel en 16 partes iguales y así te das cuenta que Fernando comió un pedazo que puede ser de 5/16, 6/16, 7/16.

También te puedes dar cuenta de que Fernando ha de ser bueno para las matemáticas, por la forma en que le dijo a su mamá qué parte del pastel se comió.

Continúa con la resolución de los retos que faltan para que sigas ejercitando la búsqueda de números entre otros dos.

Ubica los puntos que se van a indicar. En la primera ubica 1.6 y 1.7

Remarca primero los puntos 1. 6 y 1.7 después el punto 1.65

¿Qué hiciste para ubicar esos puntos en la recta?

Se coloca primero 1.6 y 1.7 dejando un espacio entre ellos. Luego, se puso un punto en medio de ellos dos.

¿Cómo decidir que valor tiene ese punto que colocaste en1 medio de los dos que se indicaron?

Que 1.6 equivae a 1 entero y 6 décimos y 1.7 es igual a 1 entero con 7 décimos, así que los décimos se pueden volver a dividir en 10 partes y serán ahora centésimos, es decir, 1.60 y 1.70 por lo tanto, como el punto está a la mitad de 1.60 y 1.70 entonces es 1.65

Ahora observa la siguiente recta, en ella vas a colocar los números 1.32 y 1.33 y deberás buscar un número que se encuentre entre ellos.

Marca primero el punto de 1.32 y luego 1.33, después señala el punto de en medio que será 1.325

Se ubican primero los puntos 1.32 y 1.33 luego hay que marcar nuevamente el punto en medio de ellos, y para saber qué número representaba había que dividir ahora los centésimos en diez partes iguales y convertirlos a milésimos, así que se encontraron estos números: 1.321, 1.322, 1.323, 1.324, y 1.325 y se identifica que ése está a la mitad de entre los dos números que se dijeron.

Ubica los puntos 1/3 y 2/3 y localiza un punto entre ellos dos que no sea el punto de en medio.

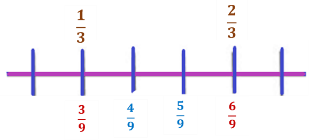
Primero, marca en la recta el punto 1/3 luego 2/3 y finalmente el punto 4/9

Primero se ubican los puntos 1/3 y 2/3 luego se pueden convertir en sextos, pero así solo se encontraba el punto de en medio y se dijo que debía encontrarse otro punto que no fuera el de en medio, así que en lugar de convertir en sextos se podía también convertir en novenos, es decir, partes aún más pequeñas, entonces como 1/3 es igual 3/9 y 2/3 es igual a 6/9 ya se puede marcar 4/9 y esta fracción está más cerca de 3/9 y no a la mitad.

Recuerda que entre cualquier par de números decimales o fracciones siempre es posible encontrar otro número decimal. Ten presente que siempre puedes seguir dividiendo en partes más pequeñas cada tramo.

El reto de hoy:

Explícale a alguien cercano los retos que enfrentaste y cómo los resolviste, seguramente le parecerá muy interesante la manera como lograste resolver cada uno de ellos.

Si te es posible, consulta otros libros y materiales para saber más sobre el tema.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/