Unidades de capacidad en el Sistema Internacional de Unidades y en el Sistema Inglés

Aprendizaje esperado: resuelve problemas que implican conversiones en múltiplos y submúltiplos del metro, litro, kilogramo y de unidades del Sistema Inglés (yarda, pulgada, galón, onza y libra).

Énfasis: usar formas eficientes para hacer conversiones de unidades en dos sistemas de medida, el Sistema Internacional de Unidades y el Sistema Inglés.

¿Qué vamos a aprender?

Estudiarás algunos conceptos matemáticos relacionados con las unidades de capacidad. Esta sesión se enfoca en aprender a realizar conversiones de unidades de capacidad del Sistema Internacional de Unidades al Sistema Inglés y viceversa.

¿Qué hacemos?

La mente es capaz de desarrollarse a medida que se alimenta con conocimiento. Cada conocimiento nuevo aumenta la capacidad de procesar información y permite tomar decisiones basadas en argumentos.

Ocupar un volumen y tener la capacidad de contener uno, son situaciones diferentes pero que están estrechamente relacionadas.

La cantidad de espacio que ocupa cualquier cosa es un valor indispensable para determinar las propiedades de cualquier objeto, sustancia o materia.

La forma que tienen algunos objetos les permite contener sustancias. Esos objetos se llaman recipientes y de ellos se puede medir tanto su capacidad como su volumen.

¿Cuál es la diferencia entre volumen y capacidad?

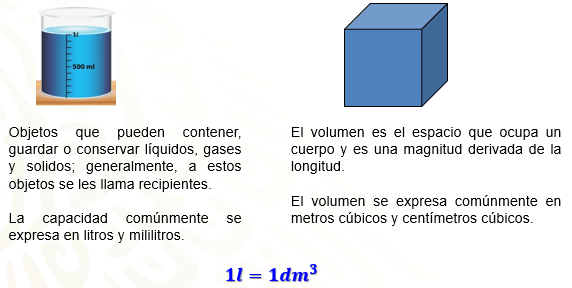
Cuando se habla de capacidad nos referimos a los objetos que pueden contener, guardar o conservar líquidos, gases y solidos; generalmente, a estos objetos se les llama recipientes. Por otra parte, el volumen es el espacio que ocupa un cuerpo y es una magnitud derivada de la longitud.

Tanto las unidades de capacidad como las unidades de volumen, indican de manera diferente el tamaño de un recipiente. Es importante tener presente que todos los objetos tienen un volumen, pues todos ocupan un lugar en el espacio.

La capacidad comúnmente se expresa en litros y mililitros, mientras que el volumen se expresa comúnmente en metros y centímetros cúbicos. Por lo tanto, entre ambos términos existe una equivalencia que se basa en la relación de igualdad entre el litro (unidad de capacidad) y el decímetro cúbico (unidad de volumen). Existen otras equivalencias que veremos más adelante.

Para tener una idea más clara acerca de la capacidad y el volumen, analiza el siguiente ejemplo y responde. ¿Cuál botella tiene mayor capacidad y mayor volumen?

En la imagen aparecen dos botellas, una con menor altura que la otra; la más pequeña con una etiqueta que dice 2 litros, mientras que la más alta con una etiqueta que dice 2 decímetros cúbicos.

Si consideramos la equivalencia anterior que, un litro es equivalente a un decímetro cúbico, es posible determinar la capacidad y el volumen de ambas botellas, por tanto, ambas botellas tienen la misma capacidad y el mismo volumen pues sus etiquetas reflejan unidades de medidas equivalentes pero que miden diferentes propiedades del objeto, mientras que la botella más pequeña tiene una etiqueta que expresa la capacidad en litros, la etiqueta de la botella más grande, expresa volumen en unidades cúbicas.

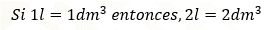
Antes de continuar, es importante hacer una aclaración sobre estas magnitudes que has estado explorando.

Oficialmente, la magnitud litro y sus derivadas, de acuerdo con la Norma Oficial Mexicana NOM-008-SCFI-2002, denominada Sistema General de Unidades de Medida, el litro no es una unidad de medida que pertenezca al Sistema Internacional de Unidades, sin embargo, acepta y conserva su uso como equivalencia al volumen.

Seguramente ya sabes que el Sistema Internacional de Unidades no es el único sistema que determina las unidades de medida en el mundo. En algunos países se utiliza el Sistema Inglés, este sistema considera sus propias medidas de capacidad; son muchas, pero en esta sesión te centrarás en las más usadas, por ejemplo, la onza de fluido que se simboliza con las letras “fl oz”; el galón que se simboliza con las letras “gal” y la taza, cuyo símbolo es la letra “c” que proviene de la palabra inglesa cup que significa taza.

Por otro lado, también centrarás la atención en el litro y metro cúbico, incluyendo algunos de sus múltiplos y submúltiplos; estas unidades de medida corresponden al Sistema Internacional de Unidades.

A continuación, se muestran algunas equivalencias entre estos sistemas de unidades y equivalencias entre unidades de capacidad y volumen.

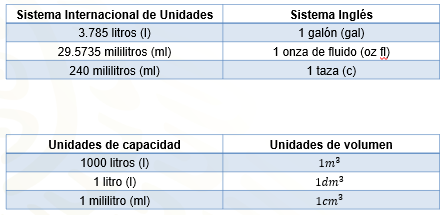
Utiliza la información que ya conoces para reflexionar, resolver y argumentar la siguiente situación experimental:

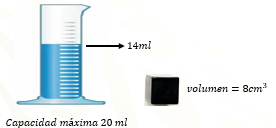
Supón que tienes un recipiente graduado con capacidad máxima de 20 mililitros, el cual contiene 14 mililitros de agua. También dispones de un cubo metálico con un volumen de 8 centímetros cúbicos. ¿Será posible introducir el cubo metálico al recipiente sin que se derrame el agua? Argumenta tu respuesta y escríbela en tu cuaderno.

Se sabe que un centímetro cúbico es equivalente a un mililitro. Si se reflexiona sobre está equivalencia y los datos de la situación planteada, es posible deducir que 8 centímetros cúbicos equivalen a 8 mililitros. Si se suman esos 8 mililitros a los 14 mililitros de agua que contiene el recipiente, se obtiene un total de 22 mililitros. A estos 22 mililitros se le resta la capacidad total del recipiente y la diferencia es igual a 2 mililitros, es decir, si se introdujera el cubo metálico al recipiente que contiene 14 mililitros de agua se rebasaría su capacidad máxima de 20 mililitros, y por consecuencia, se derramarían 2 mililitros de agua del recipiente.

¿De qué manera podrías argumentar matemáticamente esta deducción?

Una manera eficiente de generar argumentos matemáticos para realizar conversiones entre sistemas de unidades y/o unidades de medida, es utilizar factores de conversión.

Los factores de conversión, en términos simples, son un método que se utiliza para convertir valores entre diferentes unidades del mismo tipo. A grandes rasgos, consiste en multiplicar la cantidad original por una fracción en la que tanto el numerador como el denominador contengan una misma magnitud expresada en distintas unidades. Utiliza los datos de la situación anterior y establece un factor de conversión que te permita comprobar que 8 mililitros equivalen a 8 centímetros cúbicos.

Se pretende conocer la medida del cubo en función de su capacidad, por tanto, se puede establecer la siguiente operación:

El resultado es igual a 8 mililitros porque 8 por 1, entre 1, es igual a 8, expresados en mililitros porque al hacer el análisis dimensional, se simplifican los centímetros cúbicos que se encuentran en el numerador y el denominador, quedando como única unidad de medida los mililitros. Entonces, 8 centímetros cúbicos son equivalentes a 8 mililitros.

Intenta realizar este experimento, ya sea con materiales similares o con los que cuentes en casa. Después, intercambia experiencias a la distancia con tus compañeras y compañeros.

En México, de acuerdo con el Sistema Nacional de Información del Agua:

“Las presas regulan el flujo del agua en los ríos. Pueden tener uno o varios usos a la vez, entre ellos la generación de energía eléctrica, proporcionar volúmenes de agua para el riego y el abastecimiento público o controlar avenidas. La capacidad de almacenamiento de las presas del país es de aproximadamente 150 mil millones de metros cúbicos. Son 181 presas consideradas como principales y representan el 80 por ciento de la capacidad de almacenamiento nacional”.

De acuerdo con la información anterior, ¿cuántos litros de agua pueden almacenarse en 150 mil millones de metros cúbicos?

Para plantear el factor de conversión, se debe multiplicar la cantidad original, es decir, lo que se quiere convertir, por la equivalencia correspondiente escrita en fracción. Por lo tanto, se tiene que:

Capacidad en litros es igual a 150 mil millones de metros cúbicos por 1 000 litros entre un metro cúbico.

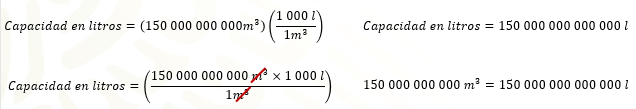
Resolviendo las operaciones y haciendo el análisis dimensional para simplificar las unidades expresadas en metros cúbicos y el resultado sea expresado en litros, tenemos que el resultado es igual a 150 billones de litros de agua. Es decir, México, a través de sus presas, tiene una capacidad de almacenamiento de 150 billones de litros de agua.

Resuelve la siguiente situación:

Para pintar la barda perimetral de una casa, Erika requiere de 90 litros de pintura en color amarillo. En la tienda de pinturas, para ese color, únicamente cuentan con la presentación en galones completos. ¿Cuántos galones de pintura deberá comprar Erika para poder pintar la barda?

Como ya dedujiste, el factor de conversión debe plantearse usando la equivalencia entre litros y galones expresado a manera de fracción, para después multiplicarlo por la magnitud que requieren convertir, en este caso, litros. El planteamiento que permite dar respuesta a la pregunta es el siguiente:

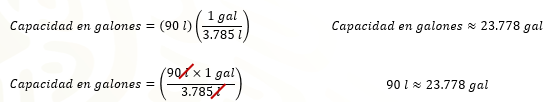
Capacidad expresada en galones es igual a 90 litros que multiplica al factor de conversión un galón entre 3 punto 785 litros. Se resuelven las operaciones indiadas: 90 litros por 1 galón, entre 3 punto 785 litros.

Con los cálculos realizados ya es posible responder la pregunta del problema y afirmar que Erika necesita comprar 24 galones de pintura amarilla para pintar la barda.

Como ya notaste, el resultado de los cálculos se redondea al número entero inmediato, ya que la tienda de pinturas no vende fracciones de galón.

Analiza la siguiente situación problemática, plantea el factor de conversión y las operaciones que requieras para responder lo que se pregunta.

Lupita quiere hacer limonada para sus compañeras del equipo de futbol donde juega. Tiene que preparar 20 litros de limonada para garantizar que ella y todas sus compañeras puedan refrescarse con la bebida. Para almacenar la limonada, Lupita, tiene dos recipientes, uno con capacidad de 2 galones y otro, con una capacidad máxima de 50 tazas. ¿Serán suficientes los recipientes que tiene Lupita para almacenar 20 litros de la limonada que tiene que preparar?

Para resolver este problema, analiza los datos que proporciona la situación y piensa en el o los factores de conversión que se deberán usar para resolverlo.

Se sabe que un galón equivale aproximadamente a 3.785 litros; uno de los recipientes que tiene Lupita es de 2 galones, esto es, aproximadamente 7.57 litros. Ahora, podemos continuar calculando la cantidad de litros que puede contener el recipiente con capacidad para 50 tazas.

Por lo tanto, se tendrá que plantear el factor de conversión para calcular la equivalencia entre tazas y litros. Si retomas las equivalencias de las tablas anteriores, notarás que no hay una equivalencia directa entre tazas y litros, pero sí hay una equivalencia que permite calcular la conversión entre tazas y mililitros.

En otras palabras, tendrás que convertir la unidad de medida tazas en la unidad de medida mililitros y posteriormente, convertir los mililitros en litros para, así, saber si el recipiente con capacidad máxima de 50 tazas junto con el recipiente con capacidad de 2 galones, serán suficientes para almacenar 20 litros de limonada.

El factor de conversión para convertir tazas a mililitros está dado por la fracción 240 mililitros entre una taza. Para realizar la conversión de unidades, deberás multiplicar este factor por la cantidad a convertir, en este caso, 50 tazas, que corresponden a la capacidad del recipiente graduado que tiene Lupita.

Entonces, se tiene que, la capacidad en mililitros es igual a 50 tazas que multiplica al factor de conversión, 240 mililitros entre una taza.

La capacidad del recipiente que tiene Lupita es de 12 000 mililitros. Ahora, debes convertir mililitros en litros, pues Lupita requiere saber si los recipientes que tiene pueden almacenar 20 litros de limonada.

Como ya sabes, para convertir mililitros en litros se debe multiplicar 12 000 mililitros por el factor de conversión dado por un litro entre 1 000 mililitros.

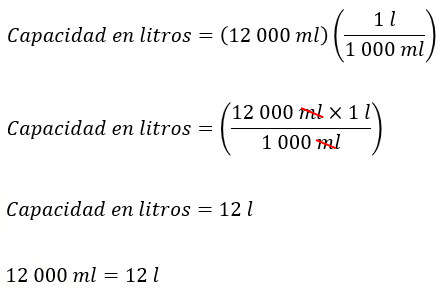
Resolviendo las operaciones, el resultado es igual a 12 litros.

Por último, suma la capacidad, en litros, de los recipientes que tiene Lupita para saber si puede almacenar la limonada que quiere elaborar.

La capacidad en litros del recipiente con capacidad de dos galones es de 7 punto 57 litros. Mientras que la capacidad en litros del recipiente con capacidad de 50 tazas es de 12 litros.

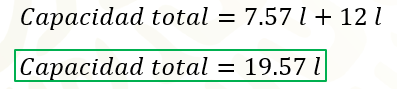
El resultado es igual a 19.57 litros, por lo tanto, los recipientes que tiene Lupita, no tienen la suficiente capacidad para almacenar 20 litros de limonada.

Determina la capacidad en tazas que le faltó al recipiente de Lupita para poder almacenar sus 20 litros de limonada.

Toma un momento para analizar y resolver la siguiente situación:

Convertir 100 onzas de fluido a litros y determinar cuántos cubos de un decímetro cúbico de volumen se necesitan para almacenar esta capacidad.

Una onza de fluido equivale a 29.5735 mililitros. Con esta equivalencia, se puede expresar el factor de conversión necesario para convertir onzas de fluido a mililitros. Sin embargo, se requiere que la conversión sea expresada en litros, por lo que deberá plantearse otro factor de conversión que permita convertir mililitros a litros, éste puede expresarse con la equivalencia un litro es igual a 1 000 mililitros.

Como seguramente ya notaste, la situación es similar al problema de los 20 litros de limonada, donde tuviste que hacer una doble conversión. Puedes repetir el mismo procedimiento o, en su defecto, hacer la conversión de forma directa, es decir, multiplicar los dos factores de conversión a la vez.

Para realizar el análisis dimensional, ten presente que únicamente se pueden simplificar las mismas unidades de medida que se encuentren tanto en el numerador como en el denominador. Bajo este argumento, es posible simplificar las onzas de fluido, así como los mililitros, quedando únicamente los litros como unidad de medida del planteamiento realizado.

Hasta este punto, ya has realizado la conversión que se requiere, pero aún falta determinar en cuántos cubos de un decímetro cúbico de volumen puede ser contenida esta capacidad.

Para resolver la situación planteada, recupera alguna información importante, por ejemplo, la equivalencia entre volumen y capacidad, en particular, la equivalencia entre decímetros cúbicos y litros. Ésta está dada por la expresión un decímetro cúbico es equivalente a un litro. También se necesitará la equivalencia entre onzas de fluido y litros que anteriormente calculaste, pues ese dato permitirá determinar el número de cubos necesarios para contener esa cantidad de litros.

Si se analizan los datos, se puede deducir la cantidad de cubos con volumen de un decímetro cúbico que se necesitan para almacenar aproximadamente 3 litros. Ya que 1 decímetro cúbico es equivalente a un litro, entonces 3 decímetros cúbicos serán equivalentes a 3 litros. Siguiendo este razonamiento, es posible decir que se necesitan 3 cubos con volumen de un decímetro cúbico para almacenar tres litros.

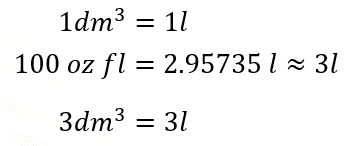
¿Cómo podrías comprobar matemáticamente este razonamiento?

Para facilitar los cálculos, redondea 2.95735 litros a 3 litros, está cantidad se multiplicará por el factor de conversión que se establezca de la equivalencia entre litros y decímetros cúbicos.

El resultado es igual a 3 decímetros cúbicos. Con estos argumentos matemáticos se pueden reafirmar las deducciones iniciales sobre esta situación.

Recuerda que este es un material de apoyo y para complementar lo estudiado, puedes consultar otras fuentes, como tu libro de texto de matemáticas de segundo grado.

El reto de hoy:

Como reto, realiza las operaciones para responder a la siguiente pregunta: ¿Cuántos cubos con volumen de un centímetro cúbico se necesitan para almacenar 3 galones de pintura?

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html

Descarga tu clase dando clic aquí