Teselados

Aprendizaje esperado: Deduce y usa las relaciones entre los ángulos de polígonos en la construcción de polígonos regulares.

Énfasis: Analizar la construcción de mosaicos (teselados) usando polígonos regulares e irregulares.

¿Qué vamos a aprender?

Analizarás las propiedades de los polígonos regulares e irregulares para construir teselados o mosaicos que cubren el plano sin dejar espacios entre sus piezas.

Seguramente has visto pisos y muros de escuelas, casas, baños, cocinas, edificios, museos y otras construcciones que están recubiertos con mosaicos o losetas que tienen un patrón geométrico, el cual cubre totalmente la superficie donde están colocados.

En esta sesión, conocerás cómo es la construcción y las características de los teselados.

¿Qué hacemos?

Reflexiona en lo siguiente:

¿Qué figuras o patrones geométricos recuerdas haber visto en pisos y muros?

Probablemente has visto algunos mosaicos formados por cuadrados, rectángulos y hexágonos.

A continuación, analiza el siguiente mosaico.

¿Encuentras un patrón?, ¿qué figuras geométricas puedes identificar?, ¿cuántos cuadriláteros distintos puedes encontrar?

Seguramente identificaste que hay cuadrados, rombos y otros cuadriláteros.

Ahora, observa las siguientes imágenes de mosaicos, a las que ahora, en Matemáticas, llamarás teselados.

Los teselados, no sólo se pueden encontrar en mosaicos para pisos y muros, también se pueden encontrar alrededor: en puertas, ventanas, portones, rejas, mallas, cercas u otros objetos.

Además, se pueden admirar los teselados en la naturaleza, por ejemplo, en este panal de abejas.

Los teselados también pueden ser imágenes creativas utilizadas para otros fines, como el decorativo o el artístico. Han existido personas, artistas, matemáticos y científicos que se han dedicado a la creación y al estudio de los teselados.

Por ejemplo, el físico matemático Roger Penrose, quien ganó este 2020, junto con dos colegas, el Premio Nobel de Física por su contribución en el estudio de los agujeros negros.

Quien también experimentó con teselados fue el artista neerlandés Maurits Cornelis Escher.

Los teselados están presentes en tu vida y han sido motivo de estudio para científicos y artistas. En casa, mira alrededor, y observa algún teselado cerca.

Ahora, reflexiona en las siguientes preguntas, anótalas y contéstalas conforme avance la sesión:

1. ¿Qué es un teselado?
2. ¿Qué características tienen los teselados?
3. ¿Cómo es que cubren el plano?
4. ¿Cómo se construyen?

Ya conoces algunos teselados, ahora identificarás sus características.

Las dos condiciones con las que debe cumplir un teselado son:

1. Los teselados cubren totalmente el plano sin dejar espacios entre las figuras que se repiten.

2. Las figuras no se sobreponen, es decir, no se enciman.

La figura base de algunos teselados están hechos con un mismo tipo de polígono regular. Entonces, ¿los teselados sólo están formados por polígonos regulares?

Para responder a la pregunta, analiza la siguiente teselación.

¿Qué figura reconoces?

En la imagen hay flechas azules que van a la derecha y otras amarillas que señalan a la izquierda. Cada una de esas flechas tiene siete lados, por lo tanto, son heptágonos, y son irregulares porque sus lados no tienen la misma longitud. Por lo tanto, los teselados también pueden estar formados por polígonos irregulares. Asimismo, se pueden combinar polígonos regulares e irregulares.

Para saber cómo, observa el siguiente teselado.

Este teselado está formado por la combinación de pentágonos regulares; por hexágonos y octágonos irregulares.

En el siguiente ejemplo, puedes darte cuenta de que en un teselado también pueden existir figuras planas, como peces y otros animales que cubren el plano.

Ahora sabes que son los teselados y conoces algunas de sus características.

A continuación, elabora tu propia definición sobre qué es un teselado y contrástala con la siguiente:

Un teselado es una figura que se repite con regularidad para cubrir el plano, es decir, tiene un patrón bien definido.

Estas figuras no dejan espacios o huecos entre ellas, ni se superponen unas con otras.

¿Pueden los triángulos equiláteros cubrir un plano?, examina la siguiente figura.

Se puede visualizar que con triángulos equiláteros sí se puede cubrir el plano, pero ¿cómo es que con este polígono regular se cubre el plano?

Para responder la pregunta anterior, observa el vértice en el que coinciden los 6 triángulos equiláteros.

¿Cuál es el ángulo interior de cada triángulo alrededor del vértice?

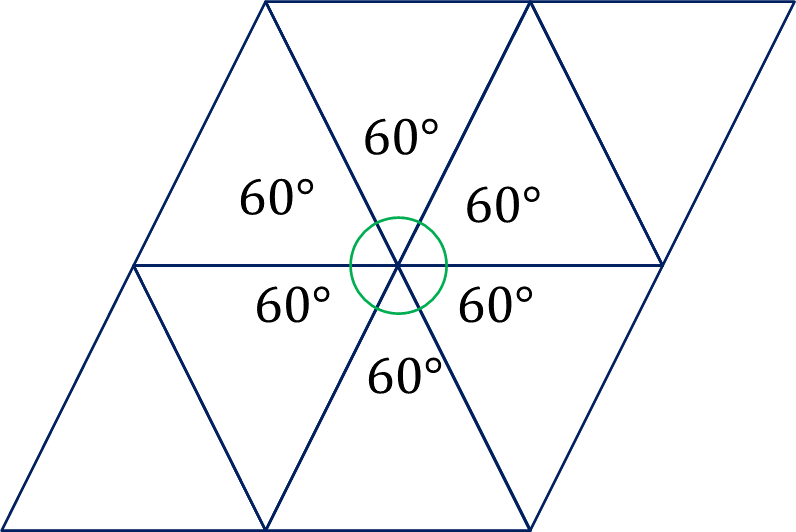
Cada ángulo interior de un triángulo equilátero mide 60 grados.

Entonces, ¿cuánto suman los ángulos interiores alrededor del vértice de los triángulos equiláteros?

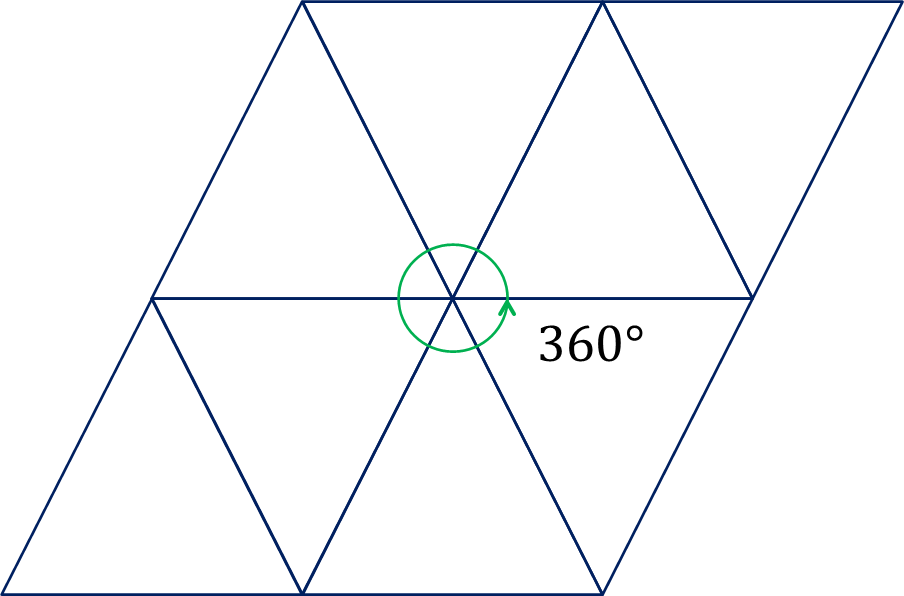
Suman 360 grados, porque son 6 por 60 grados.

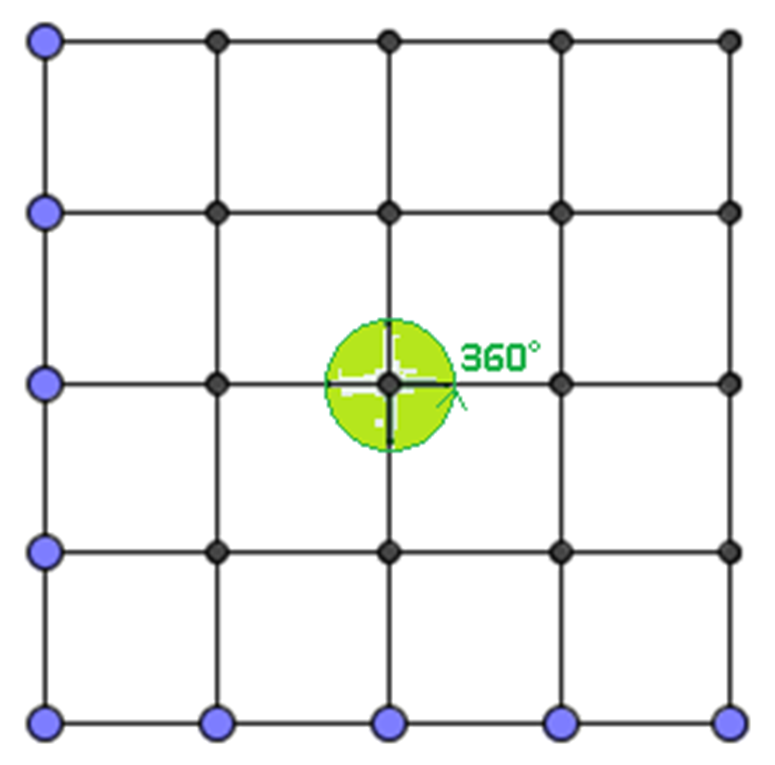
Ahora analiza una teselación formada con cuadrados de colores azul, rojo y blanco.

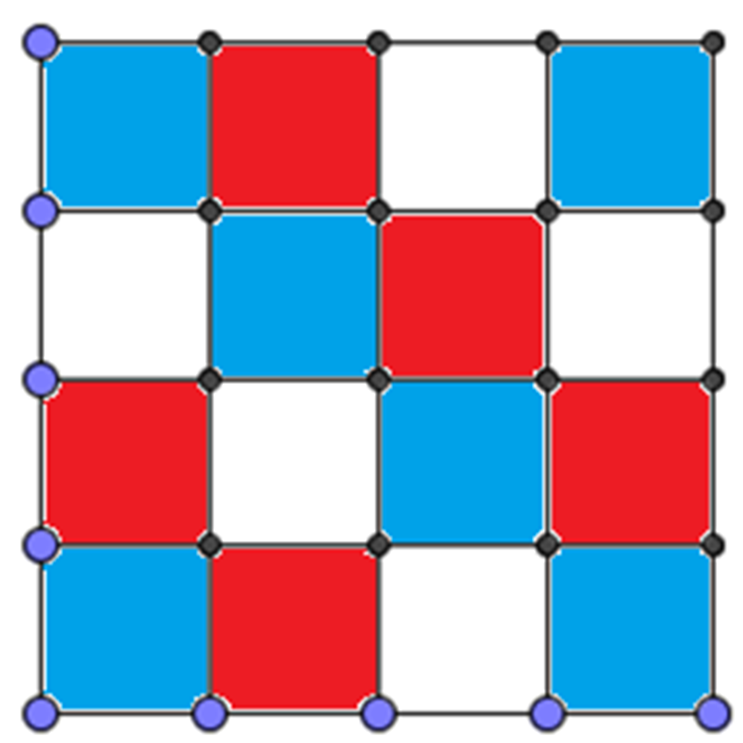
¿Cuántos cuadrados comparten un mismo vértice?

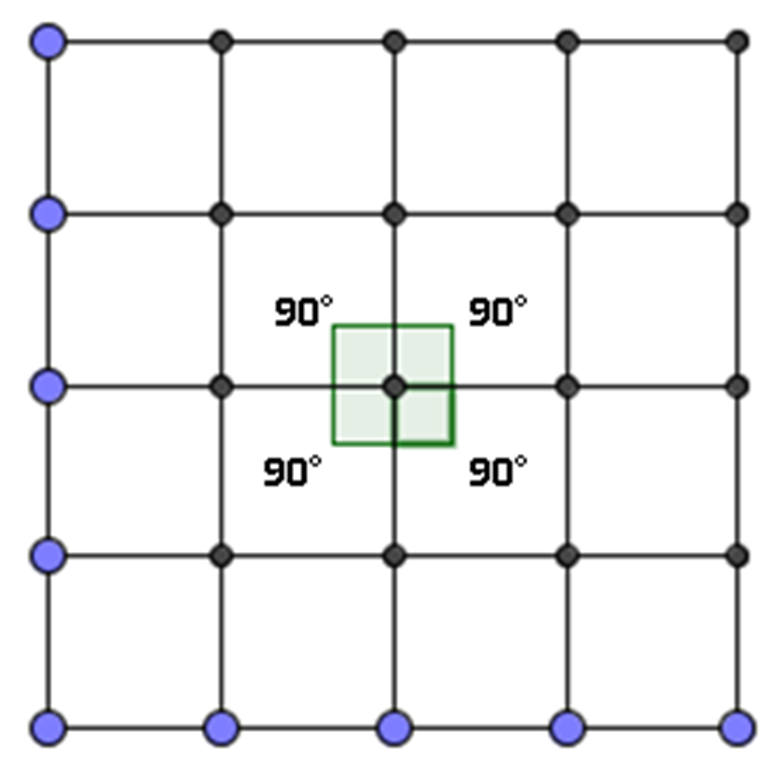
Si observaste con atención, son 4. Y el ángulo interior de cada cuadrado es de 90 grados.

Entonces, dado que hay 4 cuadrados, 4 ángulos de 90 grados, suman 360 grados, como se observa en la teselación.

¿Recuerdas el panal de abejas que observaste al inicio?

¿Cuánto miden los ángulos interiores de los hexágonos regulares y cuánto suman éstos alrededor de un vértice?

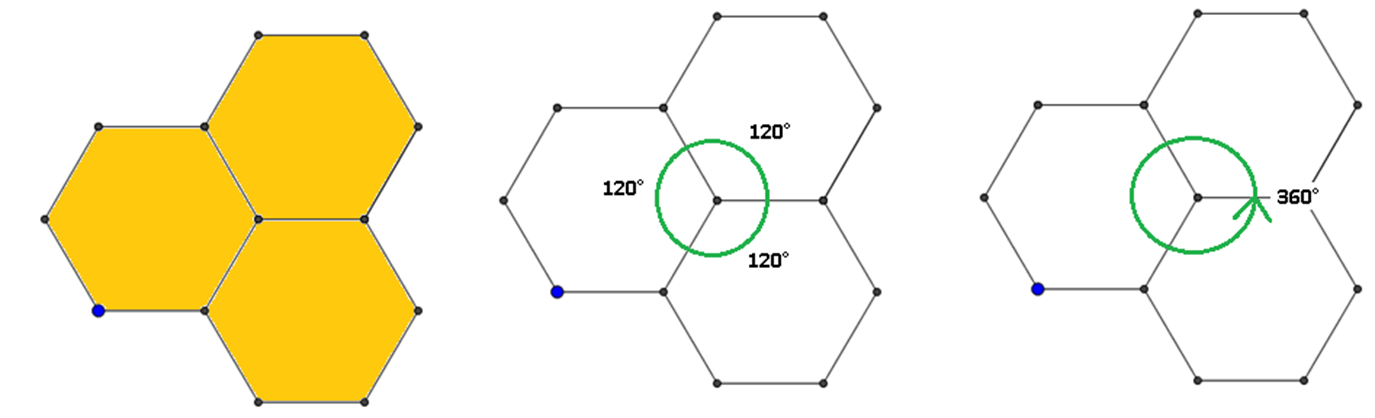
Los ángulos interiores de los tres hexágonos que coinciden en el vértice son de 120 grados y suman 360 grados.

Después de analizar estos teselados, ¿existirán otros recubrimientos en el plano que sólo utilicen polígonos regulares de la misma forma y tamaño? Para responder esta pregunta, analiza qué sucede con el pentágono regular.

Traza tres pentágonos e intenta que cubran el plano.

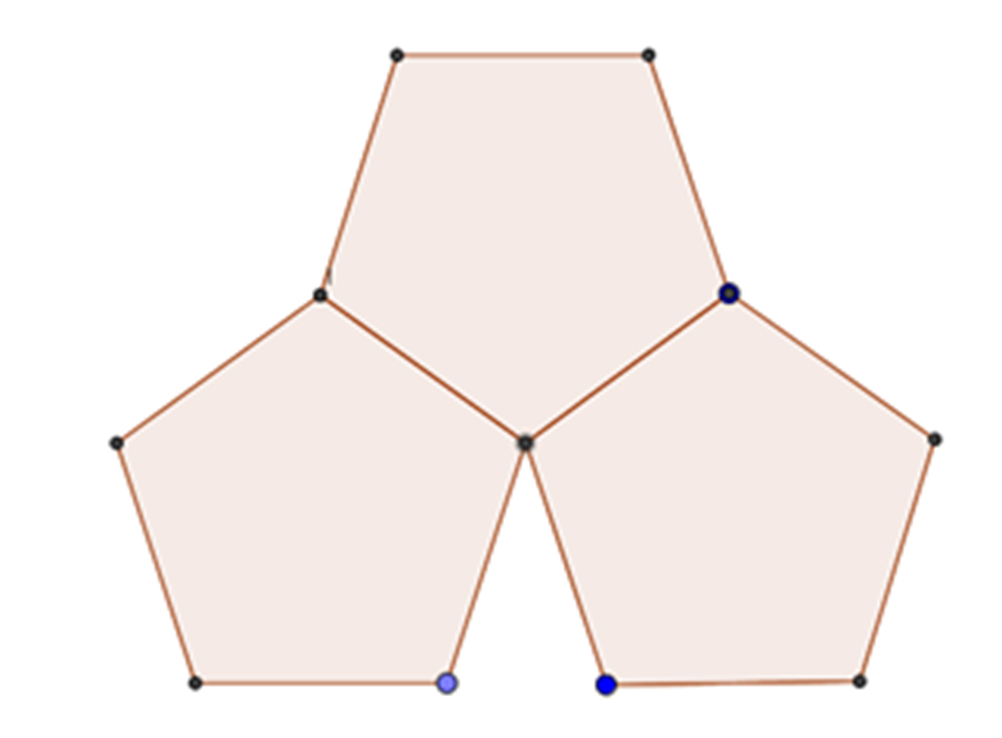
¿Qué puedes observar?

Nota que queda un espacio entre los dos pentágonos de abajo; no se cubre el plano.

¿Y si se trazan cuatro pentágonos? Observa la siguiente construcción.

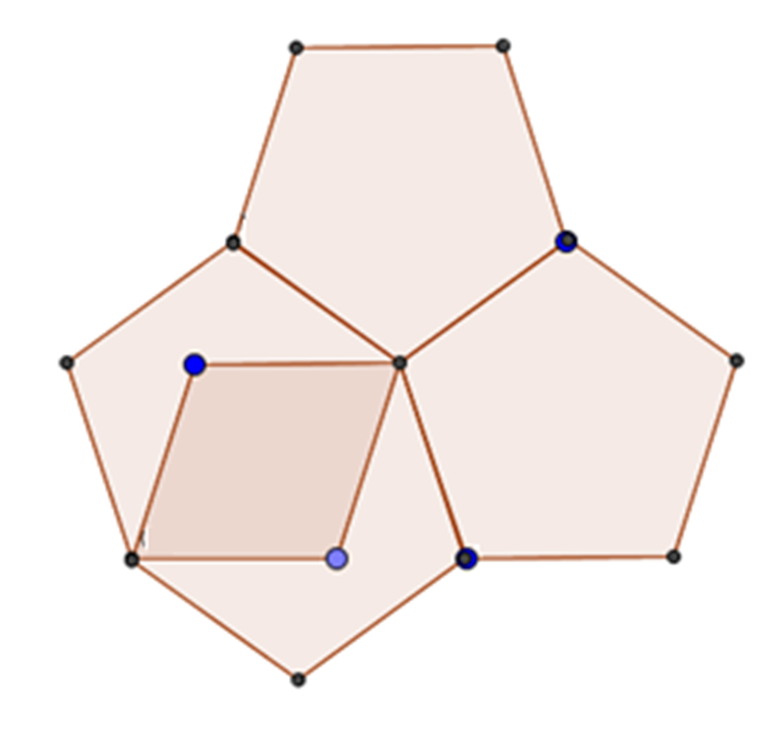
Se sobreponen, es decir, se enciman y no cumplen con la característica de un teselado.

¿Cómo se puede explicar esto?

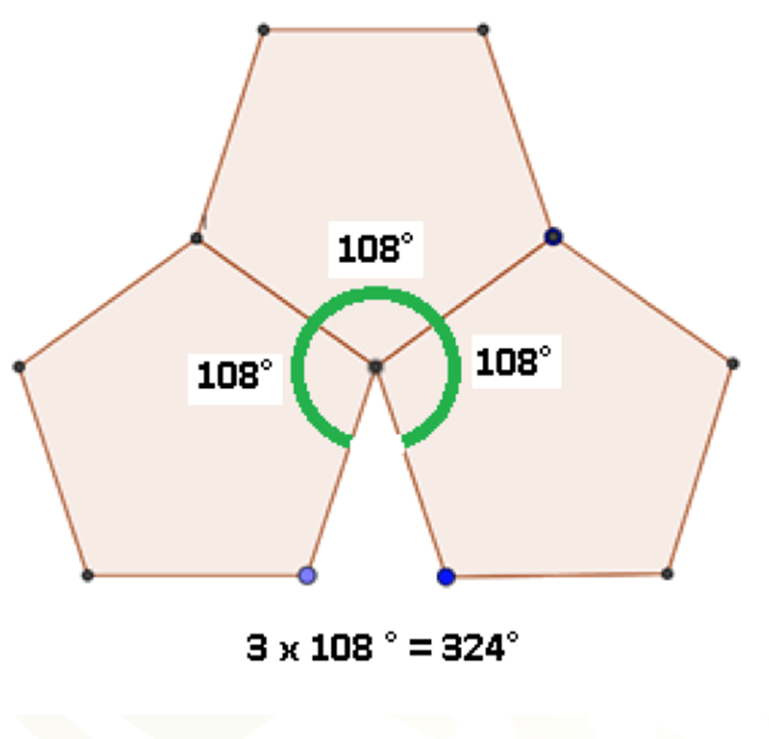
Los ángulos interiores de un pentágono regular son de 108 grados, en el caso de los tres pentágonos que se encuentran alrededor de un vértice, se tiene que el ángulo total formado por ellos es 3 por 108 grados, igual a 324 grados; esto quiere decir que faltaron 36 grados para cubrir totalmente el plano, por ello, el pentágono regular no forma teselaciones.

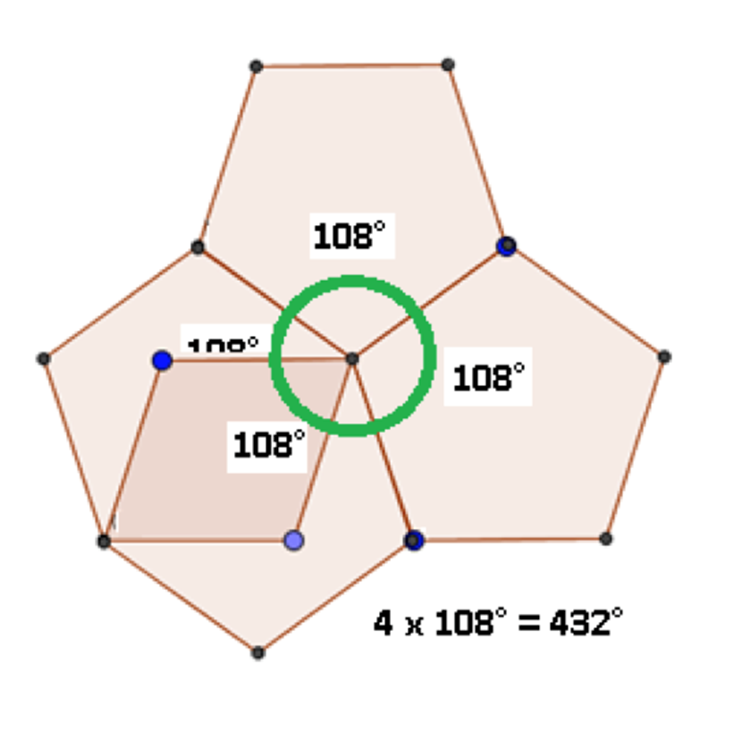
En el caso de los cuatro pentágonos, el ángulo total sería de 4 por 108 grados, igual a 432 grados; esto implica que hay una superposición de 72 grados, no cumple con una de las características de los teselados.

De este análisis, se puede concluir que:

Para que un polígono regular cubra el plano, es necesario que la suma de los ángulos interiores que coinciden en un mismo vértice sea de 360 grados, como ocurrió con los triángulos equiláteros, los cuadrados y los hexágonos.

A continuación, realiza la siguiente actividad.

Responde si se puede cubrir el plano con heptágonos u octágonos regulares y por qué. Puede ayudarte trazar en papel estos polígonos regulares, recórtalos y trata de unirlos para ver si cubren el plano.

Continúa con los teselados. Ahora, analizarás cómo se cubre el plano con dos o más tipos de polígonos regulares, también llamadas teselaciones semirregulares.

Observa las siguientes teselaciones.

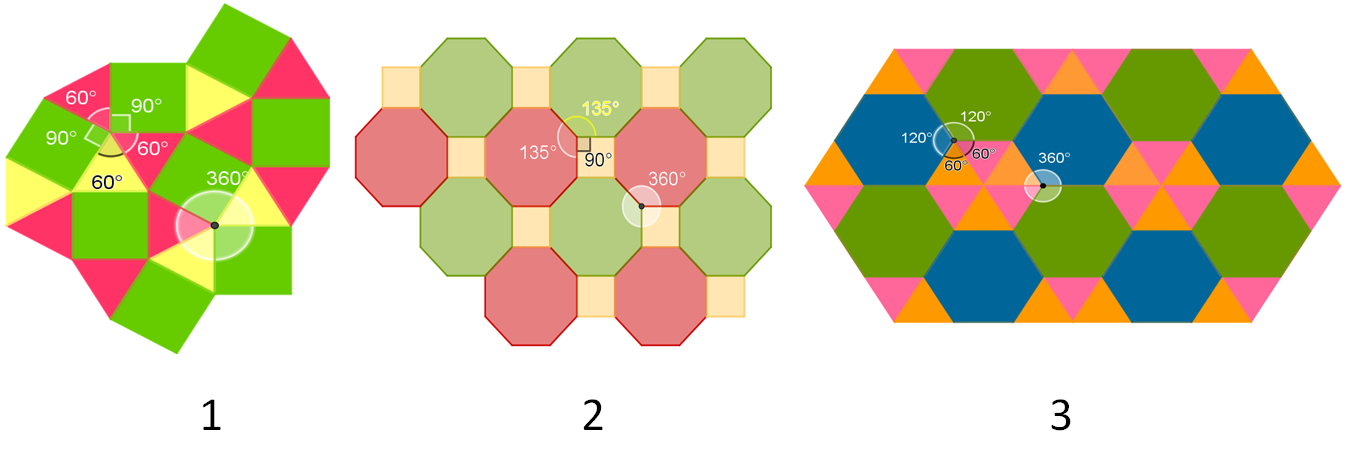
1. La teselación 1 está formada por triángulos equiláteros y cuadrados.
2. La teselación 2 está formada por octágonos regulares y cuadrados.
3. Y la teselación 3 está formada por triángulos equiláteros y hexágonos.

¿Cómo es que esta combinación de polígonos regulares cubre el plano?

Para responder, analiza cuántos polígonos coinciden en un vértice y cuánto suman sus ángulos interiores.

Teselación 1

Observa un vértice, ¿cuántos y cuáles polígonos coinciden en éste?

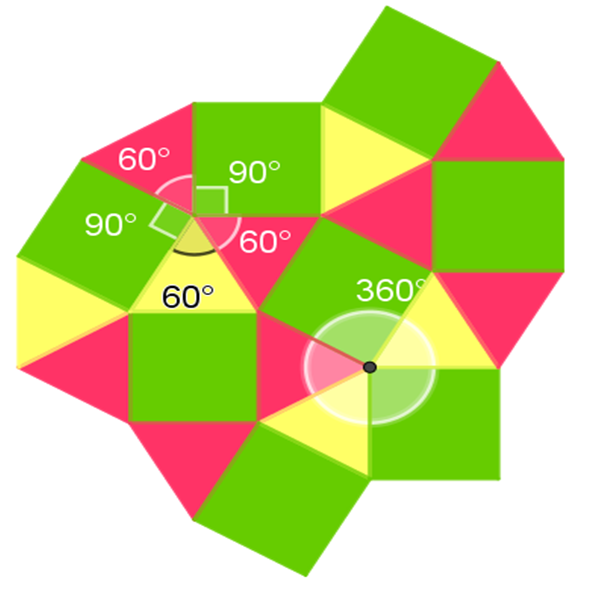
Coinciden tres triángulos y dos cuadrados.

¿Cuánto miden los ángulos interiores de estos polígonos alrededor del vértice?

Hay 3 ángulos interiores de 60 grados correspondientes a los triángulos equiláteros y dos ángulos de 90 grados correspondientes a los dos cuadrados.

¿Cuánto suman estos ángulos interiores?

Son 3 por 60 grados en los triángulos, más 2 por 90 grados en los cuadrados, esto es:

3(60°) + 2(90°) = 180° + 180° = 360°

Como puedes observar, para que se cubra la superficie con los mosaicos o teselas es necesario que, cuando se junten en un vértice, los ángulos interiores de los polígonos sumen 360 grados y, por lo tanto, estos polígonos sí cubrirán la superficie sin dejar espacios y sin encimarse.

Teselación 2

Observa el vértice donde coinciden dos octágonos regulares y un cuadrado.

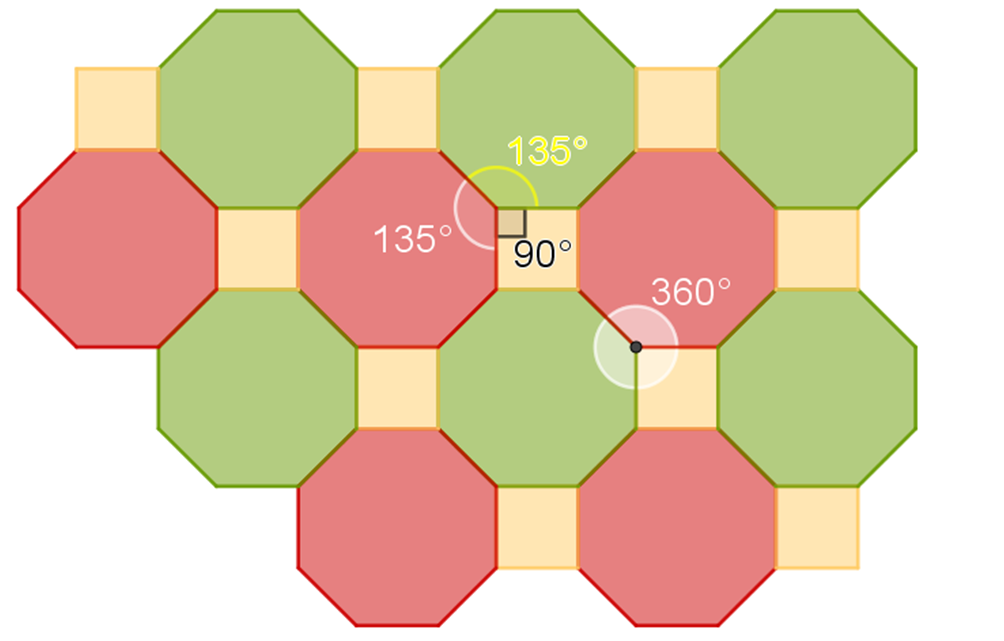
¿Cuánto miden los ángulos interiores en los octágonos y en el cuadrado que coinciden en el mismo vértice?

Sus ángulos interiores son de 135 grados en cada octágono y 90 grados en el cuadrado.

Entonces la suma total de los ángulos es 2 por 135 grados de los octágonos, más 90 grados del cuadrado; esto es:

2(135°) + 90° = 270° + 90° = 360°

Por lo tanto, esta combinación de polígonos regulares también cubre el plano sin dejar espacios y sin encimarse.

Teselación 3

¿Qué puedes observar de la teselación 3?

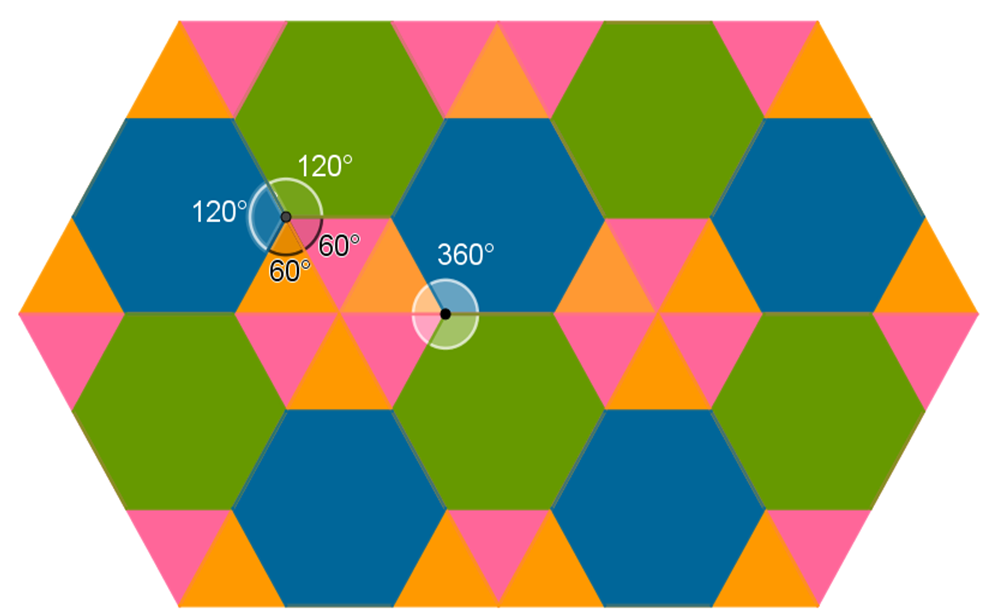
En un vértice hay dos hexágonos, los cuales tienen un ángulo interior de 120 grados y dos triángulos equiláteros, los cuales tienen un ángulo interior de 60 grados.

Si se suman los ángulos interiores de los polígonos que coinciden en un solo vértice, se tiene que:

2(120°) + 2(60°) = 240° + 120° = 360°

Suman 360 grados y cubren el plano.

Para saber cómo se cubre el plano con polígonos irregulares, observa los siguientes teselados de polígonos irregulares y verifica que en un vértice los ángulos interiores sumen 360 grados.

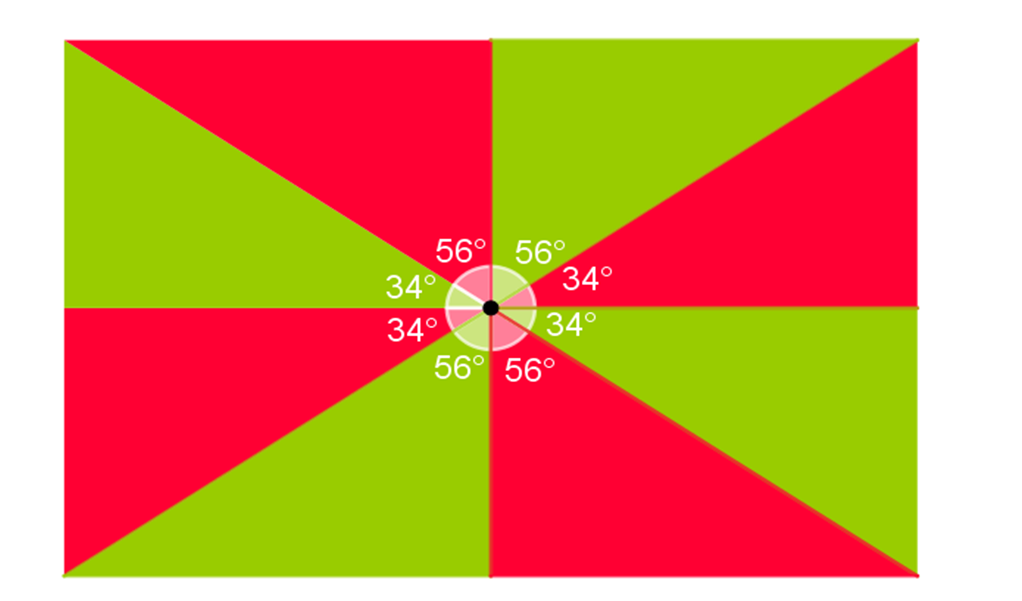
Esta teselación está formada por triángulos rectángulos escalenos; en un vértice coinciden 8 triángulos acomodados de tal forma que 4 de ellos tienen un ángulo interior de 34 grados y los otros 4 tienen un ángulo interior de 56 grados.

Si se suman estos ángulos:

4(34°) + 4(56°) = 136° + 224° = 360°

El plano queda cubierto.

La siguiente teselación está formada por trapecios isósceles.

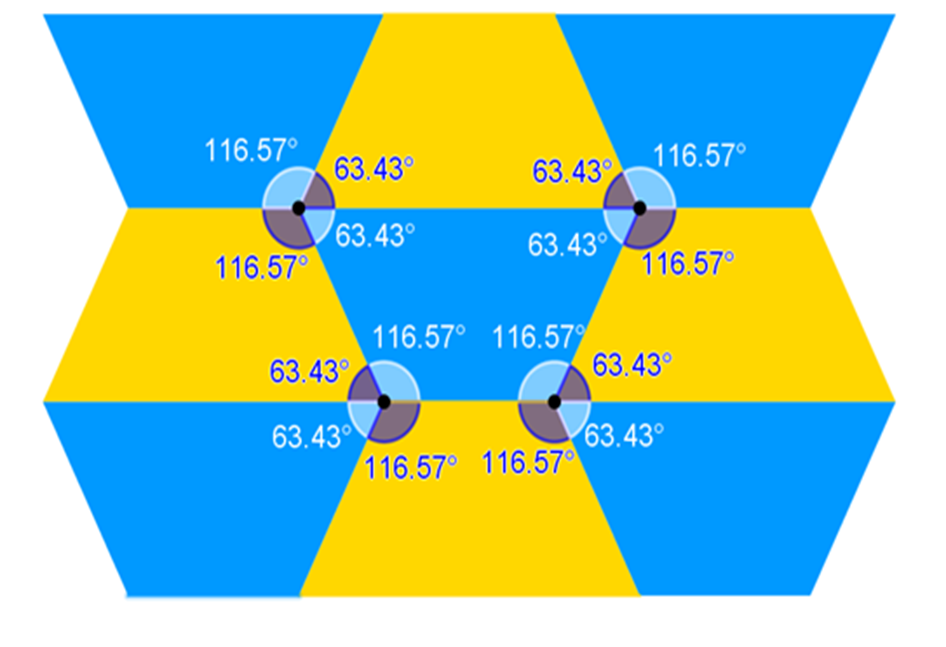
En un vértice coinciden 4 trapecios, pero acomodados de tal forma que dos de ellos tienen ángulos interiores de 116.57 grados, y los otros dos, de 63.43 grados.

La suma de los ángulos interiores en un vértice es:

2 (116.57°) + 2(63.43°) = 233.14° + 126.86° = 360°

Por ello, cubren el plano.

Ahora observa la siguiente teselación formada por hexágonos irregulares convexos, es decir, hexágonos con ángulos interiores menores a 180 grados.

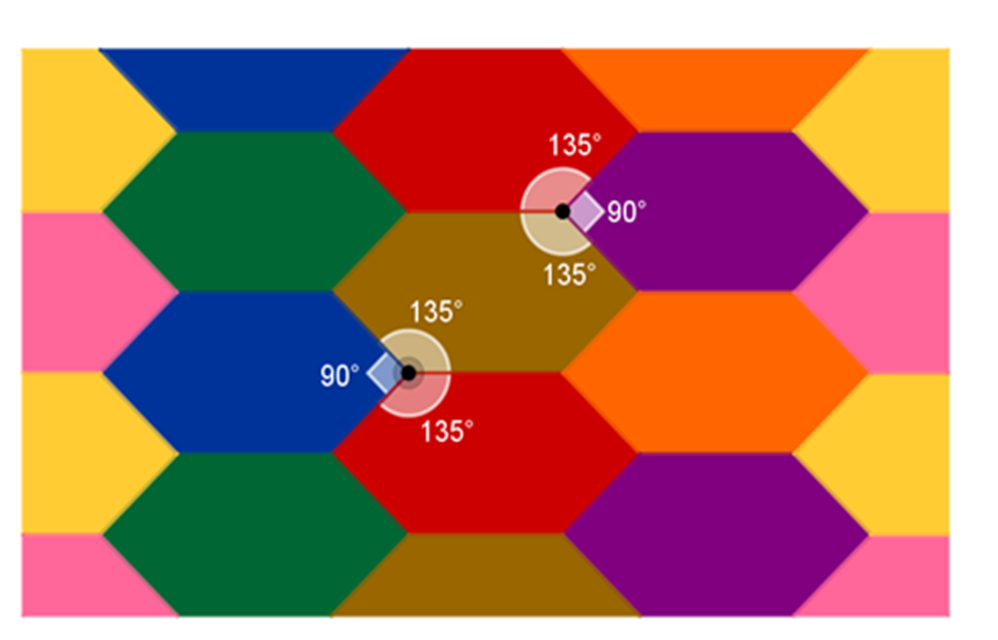
Para cubrir el plano, se suman los ángulos interiores alrededor de un vértice:

135° + 135° + 90° = 360°

También se puede formar una teselación con hexágonos irregulares cóncavos, es decir, con hexágonos en los que al menos uno de sus ángulos interiores es mayor a 180 grados.

Analiza primero uno de sus vértices.

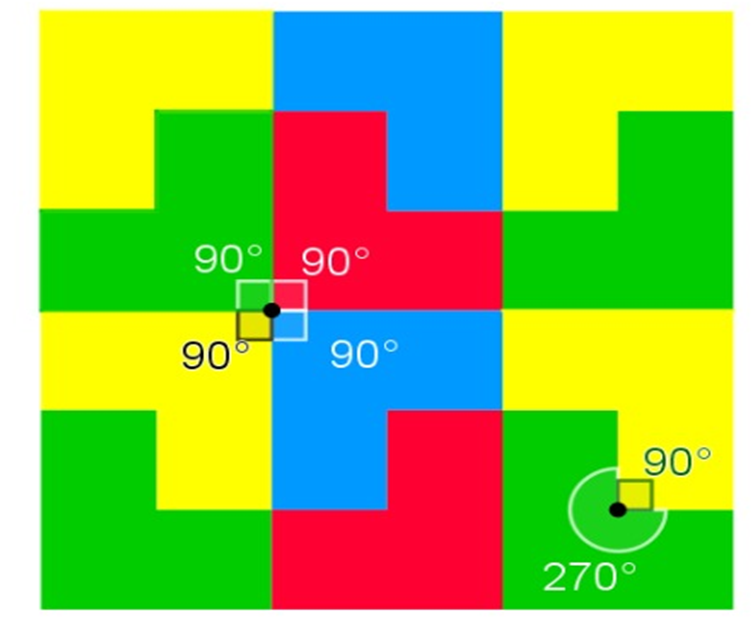
Se puede identificar que en uno de ellos que coinciden cuatro ángulos interiores de 90 grados, cuya suma es de 360 grados, por ello se cubre el plano.

También se puede observar otro vértice formado por un ángulo interior de 270 grados y otro de 90 grados, que suman 360 grados, cubriendo el plano.

Si analizas otro de los vértices, puedes notar que corresponden a cualquiera de los dos casos analizados en esta teselación.

A continuación, analiza cómo realizar teselaciones con una combinación de polígonos regulares e irregulares.

Observa la siguiente teselación.

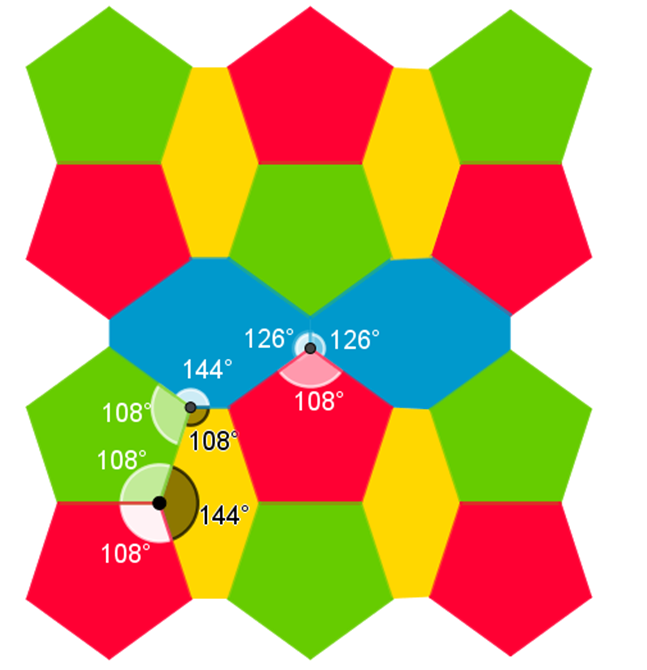
¿De qué polígonos se compone?

En esta teselación hay pentágonos regulares, octágonos irregulares y hexágonos irregulares.

¿Puedes identificar que hay 3 tipos de coincidencias de polígonos en un vértice?

En el vértice 1 coinciden dos pentágonos regulares y un hexágono irregular.

En el vértice 2 coinciden un octágono irregular, un pentágono regular y un hexágono irregular.

Y en el vértice 3 coinciden un pentágono regular y dos octágonos irregulares.

En los tres vértices se tiene que cumplir que la suma de los ángulos interiores es 360 grados.

Analiza cada caso:

En el vértice 1:

108° + 108° + 144° = 360°

En el vértice 2:

108° + 108° + 144° = 360°

En el vértice 3:

126° + 126° + 108° = 360°

En los tres vértices se cumple la suma de 360 grados y, por lo tanto, se puede cubrir el plano con este tipo de polígonos.

¿Existen otros tipos de teselados?

Se pueden incluir círculos, circunferencias, arcos, sectores circulares, combinados con teselas o mosaicos de polígonos regulares, semirregulares o irregulares, los cuales parten de un patrón matemático.

Como los encontrados en la Alhambra, complejo estratégico, militar y artístico en la comunidad de Andalucía, en la provincia de Granada, España, que es el segundo lugar más visitado de ese país por su grandiosa arquitectura neoárabe española y por sus maravillosos teselados.

También se encuentran estos teselados en el Palacio La Alhambra en Santiago de Chile, lugar en el que se replicó el arte de la vieja Alhambra.

Observa algunas teselas muy reconocidas del arte arquitectónico de Alhambra. Por ejemplo, el mosaico del hueso, que es en realidad un dodecágono irregular cóncavo.

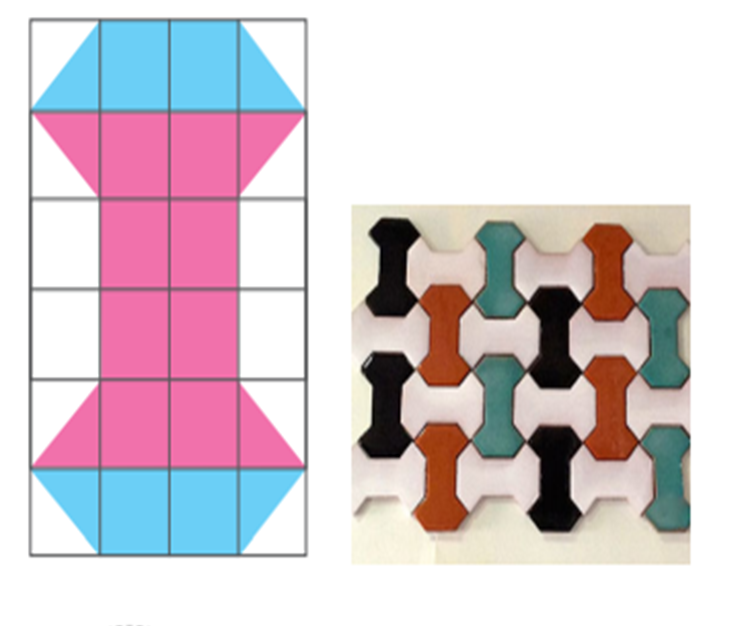
El pétalo es otro teselado utilizado en los mosaicos de Alhambra. Analiza su construcción geométrica y anota en tu cuaderno cómo la construirías.

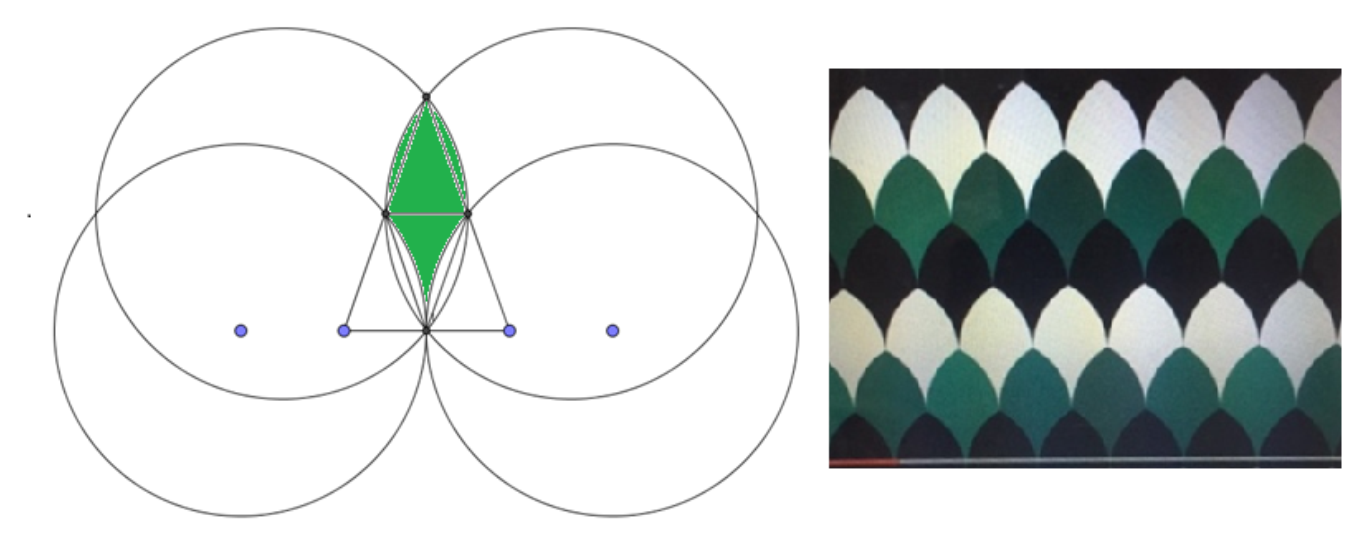
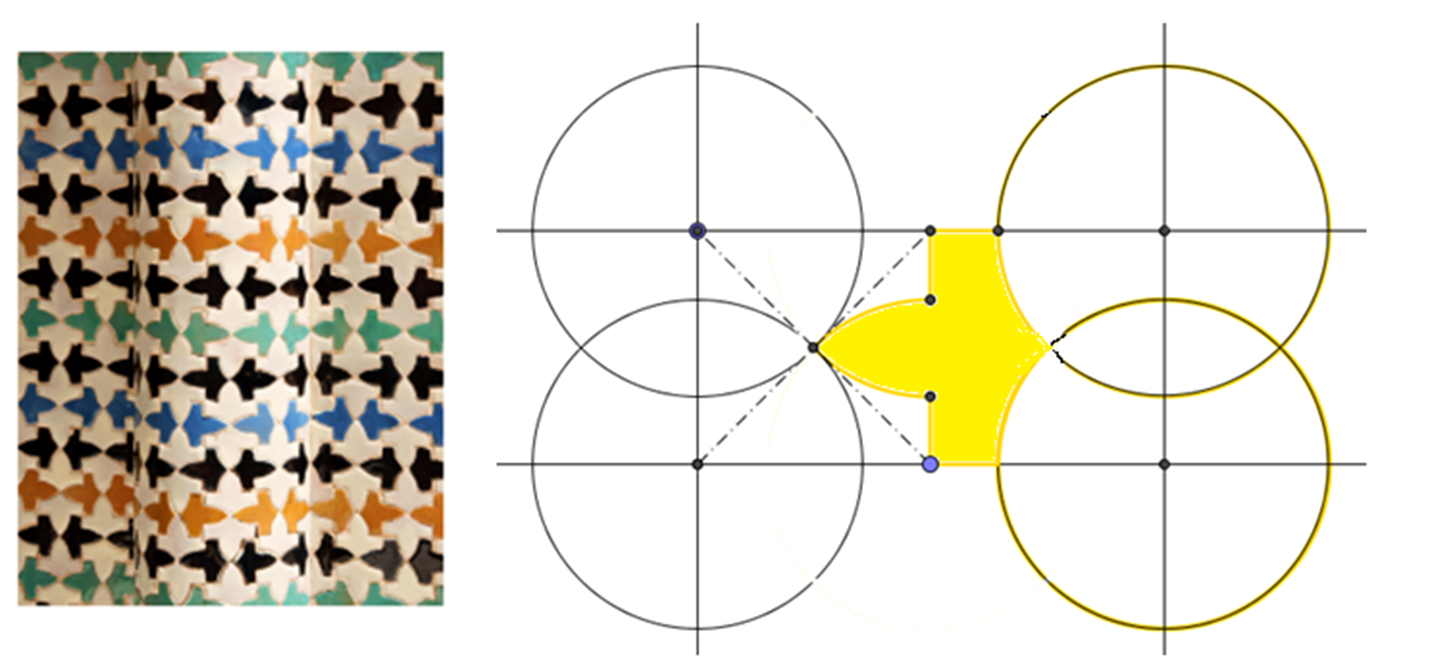
El avión es otro teselado en Alhambra, su construcción parte de cuadrados con circunferencias en sus vértices y las intersecciones de sus diagonales son puntos que forman la figura; al final se dibuja el teselado y se reproduce sobre la superficie con diferentes colores.

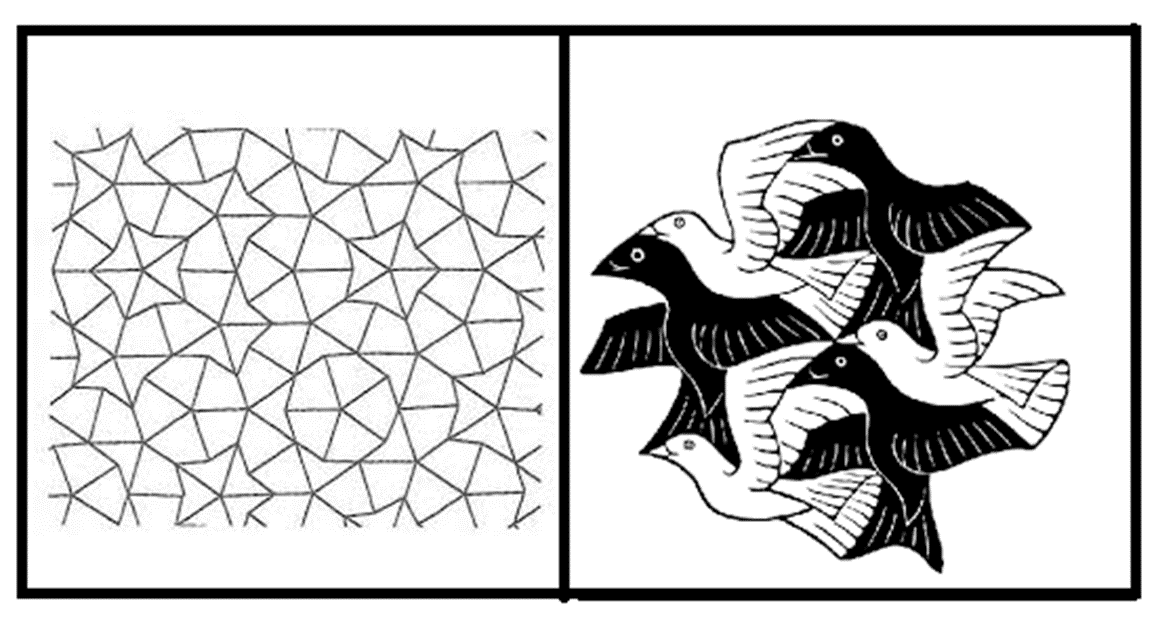
Existe otro tipo de teselados, los que han sido creación de matemáticos, científicos y artistas, como la espiral de Heinz Voderberg.

También otros irregulares con formas de animales, además de los teselados que se mencionaron al inicio, de Roger Penrose y Maurits Cornelis Escher.

En esta sesión, has viajado hacia otras culturas y te adentraste al mundo de las matemáticas y del arte.

Recapitula lo visto en esta sesión:

• Hasta este momento has visto que los teselados son figuras que cubren el plano sin dejar espacio y sin encimarse.

• Las teselas pueden estar formadas por polígonos regulares, semirregulares, irregulares o con una combinación de éstos.

• Para cubrir el plano, los ángulos interiores de los polígonos alrededor de un vértice dentro de la teselación deben sumar 360 grados.

• También analizaste teselados artísticos como los de Alhambra, basados en construcciones geométricas, y teselados irregulares formados por figuras de animales que se basan en triángulos o cuadrados, los cuales son rotados y trasladados para llenar el plano.

Recuerda que este es un material de apoyo, puedes consultar otras fuentes para complementar lo que aprendas aquí.

Consulta tu libro de texto de Matemáticas de segundo grado, seguramente encontrarás otras actividades que te ayudarán a profundizar en este tema. Es de mucha utilidad que pongas en práctica todo lo aprendido en la sesión.

El Reto de Hoy:

Con lo aprendido en esta sesión, responde las siguientes preguntas:

a) ¿Todos los triángulos pueden formar teselaciones?

b) ¿Todos los cuadriláteros pueden formar teselaciones?

Para responder estas preguntas, será necesario que realices tus construcciones en casa.

Construye 10 triángulos isósceles iguales y reacomódalos de forma que puedas verificar si se cubre el plano o no.

Además, examina los teselados con triángulos equiláteros y con los triángulos rectángulos escalenos que se analizaron en esta sesión, y determina si con cualquier tipo de triángulo se pueden formar teselaciones.

Examina también los ángulos que se forman en los triángulos alrededor de un vértice y verifica su suma.

La siguiente imagen y las que has analizado sobre triángulos, te pueden ayudar a obtener conjeturas y a contestar si todos los triángulos pueden formar teselados.

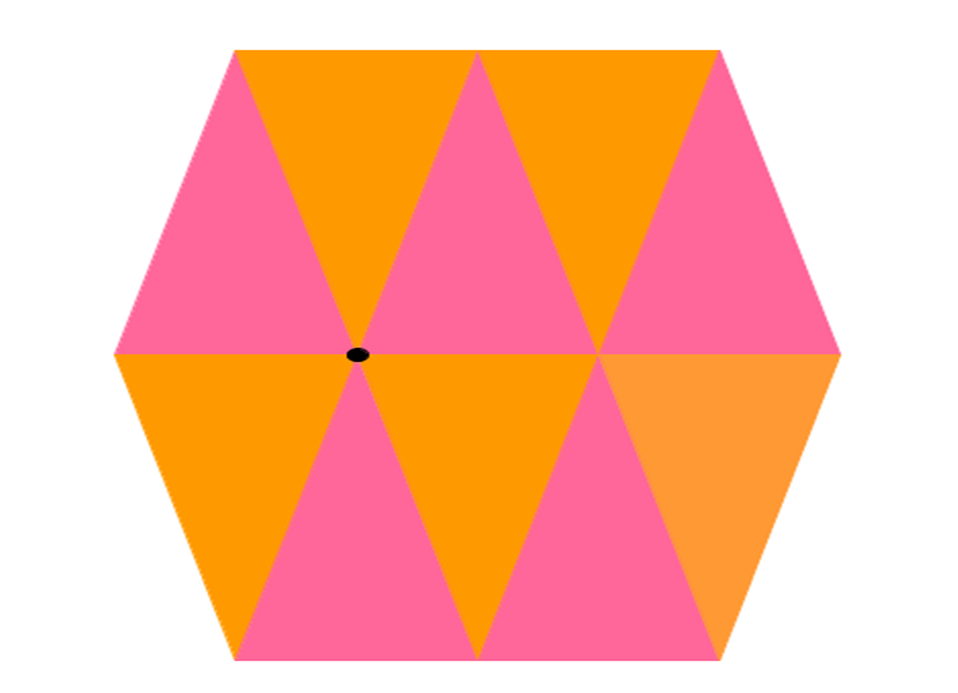
Para contestar la segunda pregunta, construye 8 rombos iguales y reacomódalos de forma que puedas verificar si con ellos se cubre el plano o no.

Además, examina los teselados con cuadrados y trapecios que analizaste en esta sesión, y compara sus construcciones.

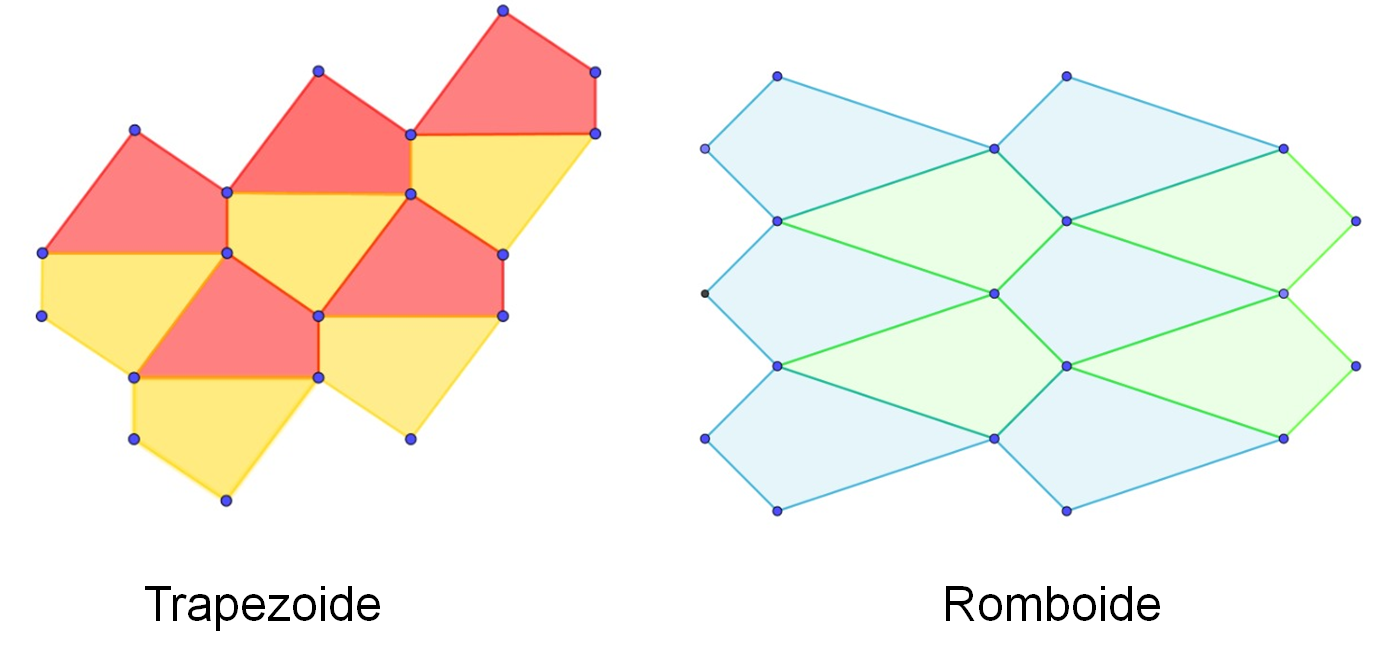
Finalmente, averigua si es posible construir teselados con rectángulos, romboides y trapezoides, tomando en cuenta los ángulos interiores de los cuadriláteros que se forman alrededor de un vértice.

Las siguientes imágenes te pueden ayudar a construir tus argumentos. Analiza los ángulos interiores de los cuadriláteros que coinciden en un vértice y verifica su suma. Escribe tus conclusiones.

Descarga tu clase dando clic

¡Buen trabajo!

Gracias por tu esfuerzo.