Sistemas de numeración

Sistemas de numeración

Aprendizaje esperado: concibe las matemáticas como una construcción social en la que se formulan y argumentan hechos y procedimientos matemáticos.

Énfasis: vincular conceptos fundamentales.

¿Qué vamos a aprender?

Ten a la mano tus materiales: cuaderno, lápiz y goma.

Ante cualquier idea o inquietud que surja al resolver las situaciones estudiadas, anota en tu cuaderno.

Los números se pueden representar usando palabras, objetos y símbolos.

El número y sus representaciones escritas que ahora conoces son producto de varios siglos de desarrollo a lo largo de la historia.

De este modo, es natural cuestionarse de dónde vienen estos símbolos, saber cómo se fueron construyendo, cómo se transmitieron entre una generación a otra, y entre culturas.

¿Qué hacemos?

El concepto de número y el proceso de conteo se desarrollaron antes del tiempo de la historia registrada. Hay evidencia arqueológica de que la humanidad empleó el conteo desde hace 50,000 años.

Cómo se fue dando este desarrollo es en gran parte conjetura; sin embargo, no es difícil suponer cómo probablemente sucedió.

Se puede argumentar que los humanos, incluso en la mayor parte de los tiempos primitivos, tenían cierto sentido numérico, al menos hasta el punto de reconocer cuando se tenían más y menos objetos, por ejemplo, cuando algunos objetos eran agregados o quitados de un grupo pequeño, ya que los estudios han demostrado que algunos animales poseen tal sentido.

Con la evolución gradual de la sociedad, el conteo simple se volvió imperativo. Una tribu tenía que saber cuántos miembros tenía y cuántos enemigos, y la humanidad encontró necesario saber si su rebaño de ovejas estaba disminuyendo de tamaño. Probablemente la forma más temprana de llevar un conteo fue mediante algún método de conteo simple.

El hombre se ha encontrado con la necesidad de contar. Esta operación la llevó a cabo, por ejemplo, al utilizar un sistema de rayas rasgadas en las paredes o pintadas en papiro, empleando el principio de correspondencia uno a uno: Una raya, un objeto.

Se ha encontrado evidencia de que los primeros humanos utilizaron cortes de madera para numerar objetos.

Otro método era hacer marcas en los troncos de los árboles o cortes sobre una vara para llevar un registro permanente.

Cada pueblo o tribu desarrolló sus propias palabras y símbolos para representar las operaciones de conteos realizados.

Con el comercio, los antiguos mercaderes estaban obligados a emplear una gran variedad de sistemas de medidas y numeración, a fin de comerciar con los diferentes pueblos o tribus.

Por estas razones, se puede argumentar que el comercio fue uno de los principales motores de la creación de registros escritos y orales.

Posteriormente, se imprimieron cuentas en la arcilla húmeda: El número de cuentas debía de coincidir con el número de impresiones.

Estas impresiones son consideradas las primeras representaciones numéricas surgidas al mismo tiempo que los registros por escrito.

Detrás de estas impresiones se unen los elementos de un conjunto con otro. Si coinciden uno a uno, entonces se tiene el mismo número de elementos de ambos conjuntos.

Asimismo, los primeros pictogramas representaron sonidos o sílabas, de las que se originan las primeras representaciones orales de los números.

Pero si bien es cierto que la invención de los números escritos se dio en un contexto de conteo de pocos elementos, pronto entraron elementos prácticos para el conteo de cantidades mayores.

Por ejemplo, la utilización de dedos de los pies y manos, frente, nariz, pecho, hombros, rodillas y tobillos.

Después de las marcas en una vara se desarrollaron varias formas para representar de manera escrita los números, conformados en sistemas. Por ejemplo, se crearon los sistemas aditivos como el egipcio, los adito-multiplicativos como los números romanos, o los posicionales como el sistema maya o indio.

Por otra parte, los numerales completos se desarrollaron en el siglo XV o XVI. Dichos numerales son los que se conocen como símbolos arábigos o indo-arábigos, con lo que ya estás familiarizado: 1, 2, 3, 4, 5, 6, 7, 8, 9 y 0.

El sistema numérico actual tiene su origen en India y tomó forma durante el periodo cultural e intelectual a lo largo del río Ganges desde la mitad del siglo III, y hasta la mitad del siglo VI, antes de nuestra era.

El sistema indio es posicional de base 10, y consta de 10 dígitos que van del cero hasta el 9.

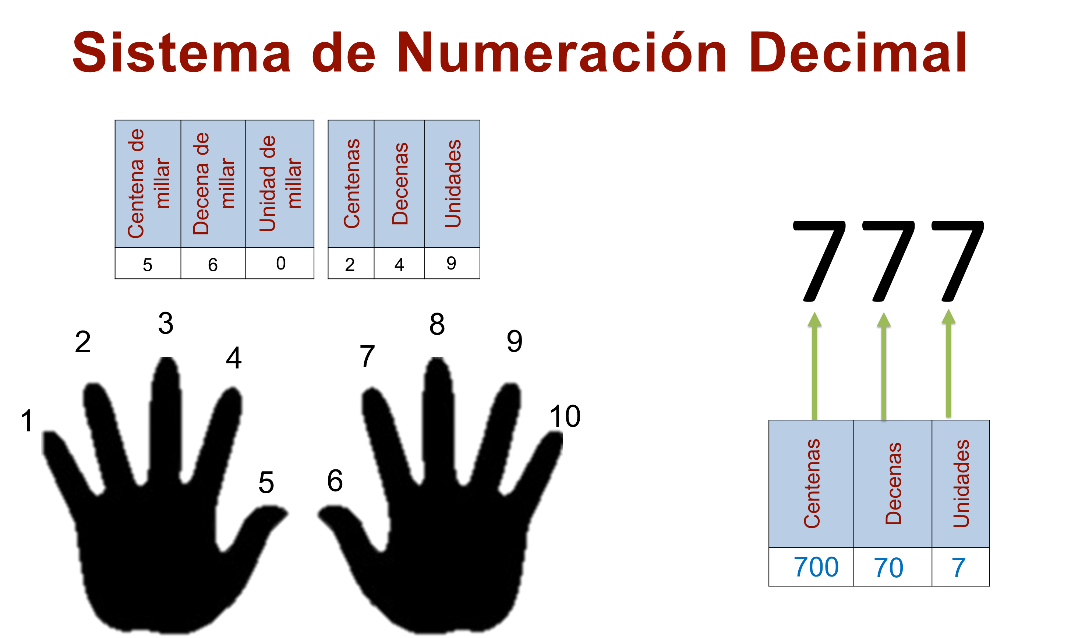
El valor de cada dígito depende del lugar que ocupa, es decir, indica cuántas unidades, decenas, y centenas, por mencionar algunas, que están representadas por ese dígito.

Así, al escribir el número 777, el dígito 7 toma tres diferentes valores de acuerdo con su posición:

El valor del primer 7 de la izquierda es 700, es decir, representa 7 centenas.

El segundo 7 su valor es 70, porque representa siete decenas, y el último 7, siete unidades.

Del ejemplo anterior, se concluye que cada valor de posición a la izquierda de otra es diez veces mayor que el de la derecha.

Es decir, 10 diez unidades son una decena.

Diez decenas son una centena

Diez centenas forman un millar, y así sucesivamente.

Y para obtener el valor de un número se debe de sumar el valor posicional de sus dígitos.

Sigue con otro ejemplo:

En el número 6 914, el dígito 6 en la posición de unidades de millar, su valor es 6,000.

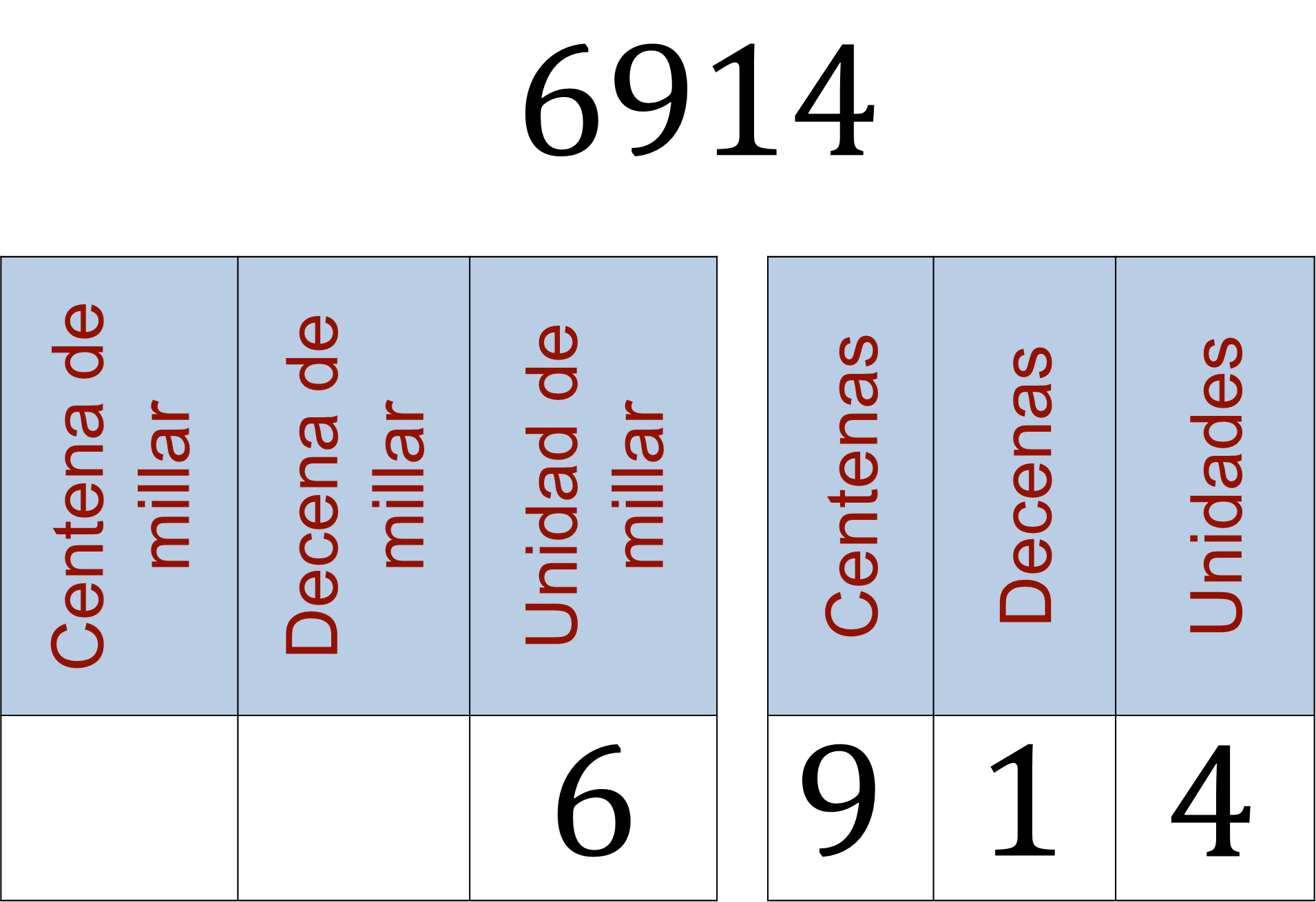
El dígito 9 ocupa la posición de las centenas; su valor posicional es 900.

El dígito 1 ocupa la posición de las decenas, por tanto, su valor es 10.

Finalmente, el dígito 4 ocupa la posición de las unidades y vale 4.

Realiza un ejercicio con la primera conclusión.

En cada inciso se muestra una cantidad distinta; en ellas el número 3 aparece en color azul.

Identifica el valor posicional del número 3 para cada cantidad.

Para conocer el valor del número indicado, se observa la posición que representa.

En cada cantidad se puede ocupar la tabla posicional y si ya se tienen los valores posicionales, se comprueban:

En el inciso a), el valor del número 3 es 30 porque representa 3 decenas.

En el inciso b), el valor posicional del 3 es 3 unidades.

El valor posicional del 3 en 79,310 es 300.

Y en el inciso d), el valor posicional del 3 es 3,000.

Conoce un ejemplo sobre la segunda conclusión: Para obtener el valor de un número se debe de sumar el valor posicional de sus dígitos.

El número 75,269 se puede descomponer de la siguiente manera:

75,269 es igual a 70 000, más 5,000, más 200, más 60, más 9.

O bien, se puede expresar el valor posicional de cada dígito mediante un producto.

75,269 es igual a 7 por 10,000, más 5 por 1,000, más 2 por 100, más 6 por 10, más 9 por 1.

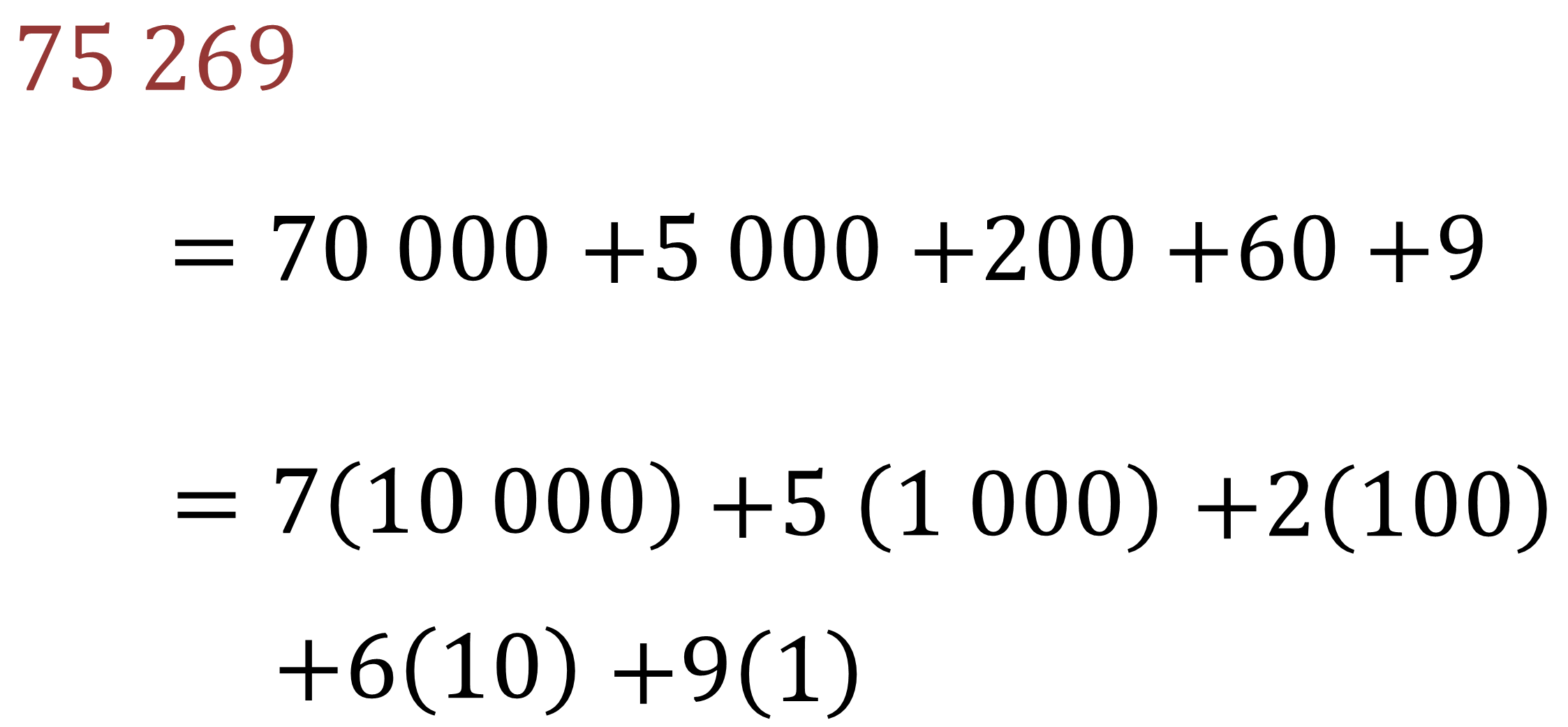
Para representar números decimales se utilizan las mismas relaciones de equivalencia entre los órdenes de unidades, pero en orden decreciente.

Surgen así las décimas, centésimas, milésimas, diezmilésimas y así sucesivamente.

También es posible descomponer un número decimal de manera análoga, tal como lo hiciste con los números naturales.

Por ejemplo, el número 7.483 milésimos se puede descomponer de la siguiente manera:

70 más 2, más 0.4 décimos, más 0.08 centésimos, más 0.003 milésimos.

O bien,

7 por 10, más 2 por 1, más 4 por 0.1,

más 8 por 0.01, más 3 por 0.001.

Cabe destacar que el sistema decimal es sólo una manera para representar números.

Existen otros sistemas de numeración con bases diferentes, por ejemplo:

Con base 20 o vigesimal, como los mayas.

Base 60 o sexagesimal, que empleada en la unidad estándar se le conoce como “grado”.

Así también existen sistemas de numeración donde no importa la posición de los símbolos, sino el conjunto de ellos, como es en el sistema egipcio.

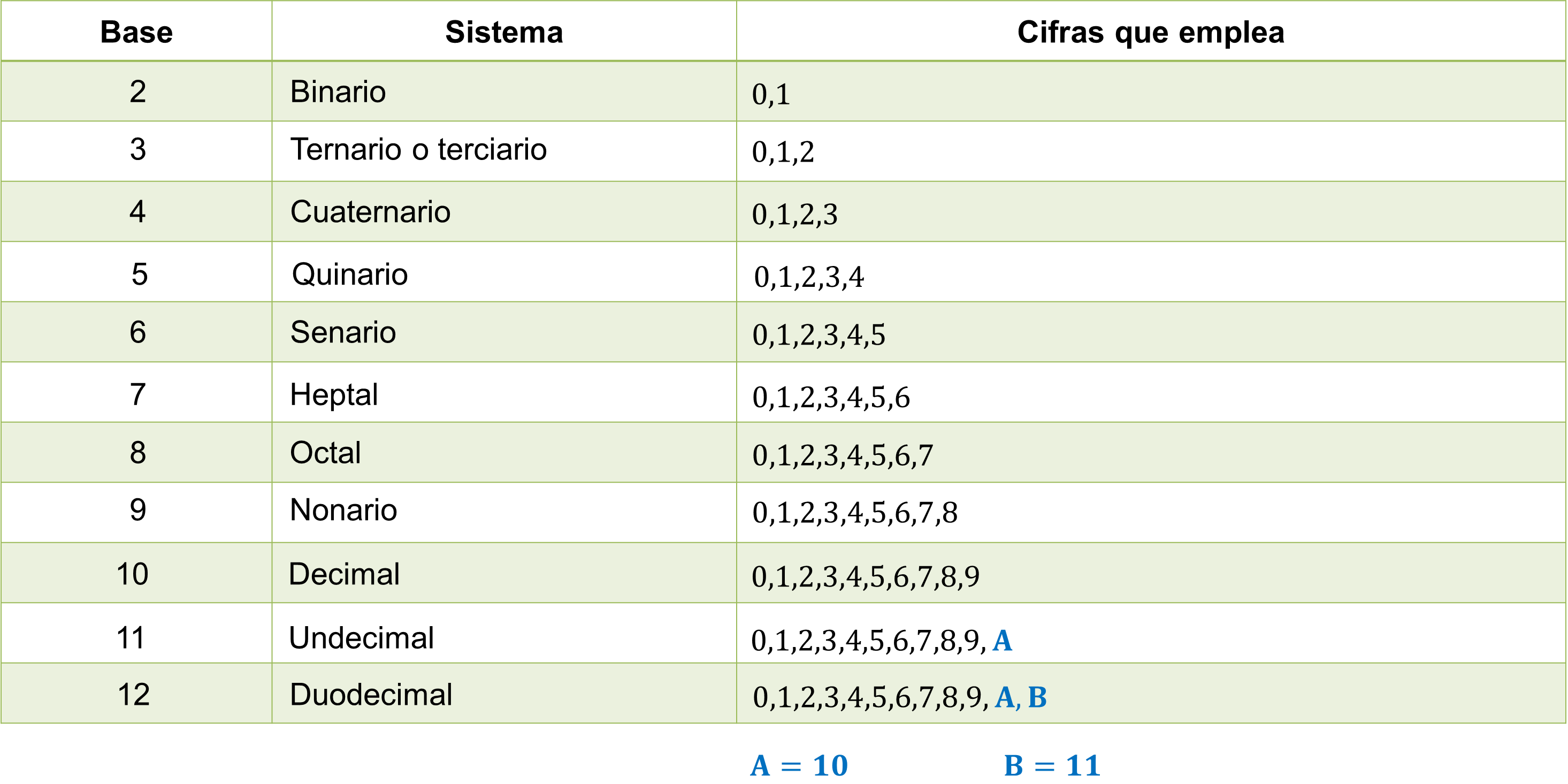
En este sentido, la base de un sistema de numeración también indica cuántas cifras pueden usarse en el sistema.

Por ejemplo: El sistema binario ocupa el 0 y el 1; el ternario o terciario ocupa el 0, 1 y 2; el cuaternario ocupa cuatro cifras del 0 al 3; el quinario sólo 5 cifras: 0, 1, 2, 3 y 4.

El senario es de 6 cifras del 0 al 5, y así sucesivamente.

Base 7 del 0 hasta el 6, base 8 del 0 hasta el 7, base 9 del 0 hasta el 8, base 10 del 0 hasta el 9, base 11 del 0 al 9 y una representación del 10, ya que no se puede utilizar el 1 y el 0 juntos porque son dos cifras.

Se presenta el mismo caso en el sistema duodecimal, es decir, de base 12, del que se ocupa del 0 al 9, A y B.

Realiza otro ejercicio en el que emplees los conocimientos adquiridos hasta el momento.

Los números con dos o tres cifras están escritos en distintas bases.

Analiza y registra cuáles de éstas pueden existir en la base numérica indicada y cuáles no.

Toma en cuenta las cifras empleadas en cada base de los sistemas de numeración solicitados.

Se analiza a continuación otro de los ejemplos para determinar si están escritos en la base indicada.

En el inciso a) 341, base 5, se comprueba si cada uno de sus dígitos corresponden a los empleados por la base:

3 es menor que la base 5, 4 es menor a 5, y 1 es menor a 5. Por lo tanto, este número sí está escrito en base 5.

Inciso b) 643, base 10, los dígitos 6, 4 y 3 son menores a la base, y sí son óptimos para la base indicada.

Inciso c) 978, base 2, tanto el dígito 9, 7 y 8 son mayores a la base 2, por lo tanto, no pueden ser base 2.

Inciso d) 978, base 9, como el dígito 9 es igual a la base, se descalifica.

Inciso e) 978, base 10, los tres dígitos 9, 7 y 8 son menores a la base, y sí puede ser en esa base.

Inciso f) 120, base 3, tanto el 1, 2 y 0 son menores a la base y sí cumplen con la condición.

Inciso g) 122, base 2, el dígito 1 es menor a la base, pero los dígitos 2 son iguales a la base, por lo tanto, se descalifica.

E inciso h) 10, base 10, los dígitos 1 y 0 son menores a la base.

Comparte tu razonamiento con familiares y amigos. Asimismo, si tienes alguna duda, anótala en tus cuadernos y consulta con tus maestros de matemáticas.

Se tiene además otro sistema de numeración con base 20. Éste fue creado por una civilización que se dio lugar en nuestro territorio mexicano, en Yucatán: los Mayas.

Observa el siguiente audiovisual del inicio al minuto 01:37 para que tomes nota de la forma de representación de los números.

• Los números mayas

https://youtu.be/HcWkDy864cE

El sistema de numeración Maya, a diferencia del sistema de numeración decimal, es base 20 y consta de tres símbolos: Una semilla o caracol, el punto y una línea horizontal.

La semilla o caracol representa el 0, el punto representa el 1 y la línea horizontal representa 5.

Los Mayas agrupaban las cantidades de 20 en 20 y tenían niveles.

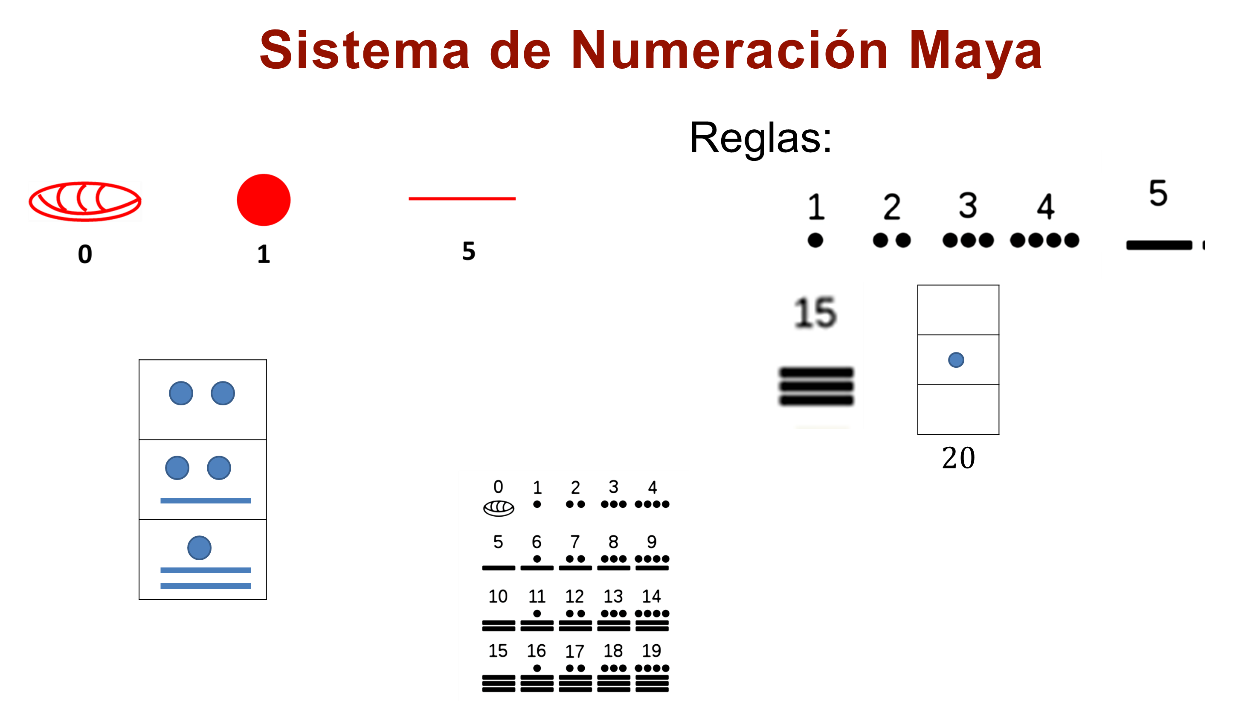
Las dos reglas para los símbolos eran: Que el punto se puede repetir hasta 4 veces, así que en lugar de dibujar 5 puntos para el número 5, dibujaban una línea horizontal.

Y la segunda regla es que la raya o línea horizontal se puede repetir hasta 3 veces. Es así como para representar el número 20, en vez de 4 líneas, se colocaba un punto en el nivel superior. De esta manera, el número mayor que se podía formar por cada nivel era el número 19.

El sistema de numeración Maya tiene niveles en su escritura y en los valores para cada casilla.

Cada nivel superior se multiplica por 20 a la potencia correspondiente.

Así el nivel 1 se multiplica por 20 a la potencia cero, es decir, por la unidad.

El nivel 2 se multiplica por 20 a la potencia uno, es decir, por 20.

El nivel 3 por 20 al cuadrado igual a 400, y el nivel 4 por 20 a la tercera potencia igual a 8,000.

Con esto, se conoce un ejemplo sobre cómo convertir un número Maya al sistema de numeración decimal o base 20.

Identifica el número formado en cada nivel, para esto, suma el valor de cada símbolo.

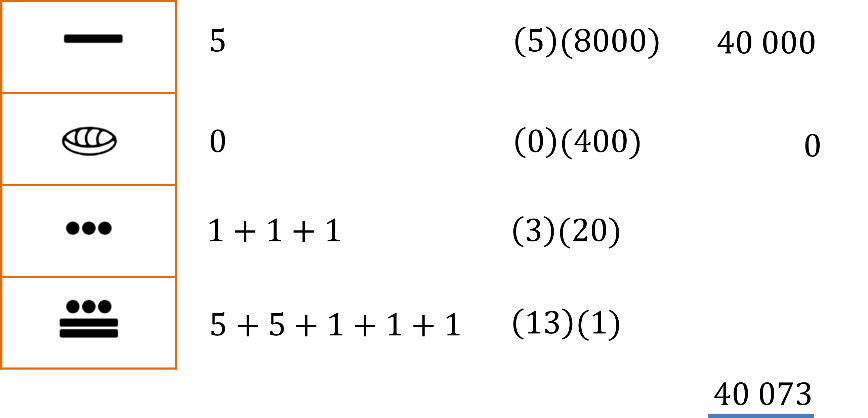
Así en el nivel 1 hay 2 líneas y tres puntos, los cuales equivalen a 5, más 5, más 1, más 1, más 1, igual a 13, por 1 por ser el primer nivel igual a 13.

En el nivel 2 hay 3 puntos, su valor es 3 y al ser nivel 2, se multiplica por 20; el resultado es 60.

En el nivel 3 hay un caracol cuyo valor es cero, multiplicado por 400 es cero.

Y en el nivel 4 hay una línea horizontal que representa 5 que al multiplicar por 8,000, es igual a 40,000.

Al final, se suman los resultados de cada nivel y se tiene que el valor del número maya en sistema decimal es 40,073.

El sistema de numeración Maya resulta sencillo porque tiene pocos símbolos y utiliza niveles; cada casilla se puede ocupar hasta un cierto valor. Después de ello, se debe de sustituir el símbolo y pasar al siguiente nivel.

Pero ¿te imaginas si se tuviera un sistema base 60? ¿Sabías que este sistema sexagesimal se usa de manera frecuente?

Es un sistema de numeración en donde cada unidad se divide entre 60 unidades de orden inferior, es decir, es un sistema de numeración de base 60.

En la actualidad, persisten dos aplicaciones del sistema sexagesimal que conoces bien. Éstas son:

1. La medida de ángulos en grados, minutos y segundos, por ejemplo: 23 grados 15 minutos 47 segundos.
2. Y la subdivisión del tiempo: Una hora se divide en 60 minutos y un minuto, en 60 segundos.

Aplica lo aprendido acerca de los sistemas numéricos decimal y sexagesimal para convertir cantidades en ambos sistemas.

Convierte 20 grados 30 minutos al sistema decimal. Para convertir del sistema sexagesimal al sistema decimal:

• Los grados se convierten en número entero, en este caso 20.
• Los 30 minutos, para convertirlos a número decimal, se dividen 30 entre 60, que son los minutos en una hora. El resultado es 0.5; así 30 minutos es igual a 0.5.
• Como resultado se tiene 20 grados 30 minutos, es igual a 20.5 grados.

Para convertir del sistema decimal al sistema sexagesimal se hace un procedimiento similar, pero se emplea una multiplicación:

Para convertir 25.2 grados al sistema sexagesimal:

• Los enteros se pasan a grados directamente. En este caso 25 es igual a 25 grados.
• Para convertir el 0.2 a minutos, se multiplica por 60 minutos que hay en una hora, es decir, 0.2 por 60, igual a 12 minutos.
• Por lo tanto, 25.2 grados es igual a 25 grados 12 minutos.

Realiza un último ejercicio.

Responde lo más rápido posible y con la mayor cantidad de respuestas correctas.

Pregunta 1:

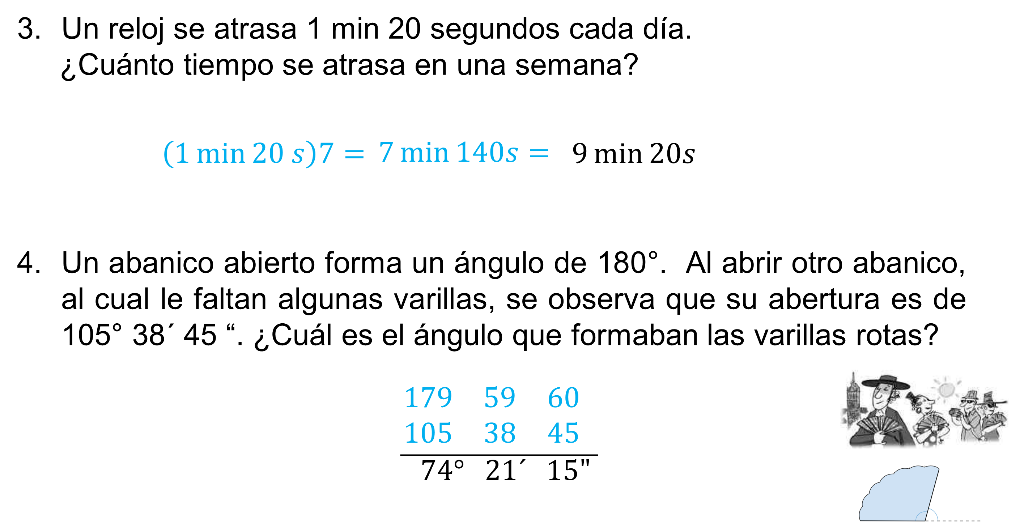
180 grados equivalen a 179 grados, 59 minutos con 60 segundos, menos 105 grados, 38 minutos, 45 segundos.

Así, el ángulo de las varillas rotas es 74 grados 21 minutos 15 segundos.

Revisa lo aprendido.

Los números se pueden representar usando palabras, objetos y símbolos.

El sistema de numeración decimal o de base diez se extiende infinitamente a números muy grandes o pequeños, por ejemplo, millones o millonésimas.

Para cualquier número, el lugar de un dígito indica cuántas decenas y centenas, por mencionar algunos, están representadas por ese dígito.

Cada valor de posición a la izquierda de otra es diez veces mayor que el de la derecha.

Y se puede sumar el valor de los dígitos para obtener el valor del número.

El reto de hoy:

Revisa tu libro de texto para aprender más sobre el tema y otras fuentes de apoyo disponibles en la página de CONALITEG.

Del mismo modo, manifiesta las dudas con tus maestros y maestras de Matemáticas, o consulta otras fuentes de apoyo para resolverlas.

Lee la siguiente cita del matemático italiano, Galileo Galilei: “No podemos enseñar nada a nadie. Tan sólo podemos ayudar a que descubran por sí mismos”.

¡Buen trabajo!

Gracias por tu esfuerzo.

* Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.