Sistema de ecuaciones. Método de igualación
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:23
Sistema de ecuaciones. Método de igualación
Aprendizaje esperado: resuelve y plantea problemas que involucran ecuaciones lineales, sistemas de ecuaciones y ecuaciones de segundo grado.
Énfasis: resolver problemas que implican un sistema de ecuaciones lineales utilizando el método de igualación.
¿Qué vamos a aprender?
Ten a la mano tu cuaderno, lápiz y goma.
El método de igualación es una de las varias formas de encontrar los valores de las incógnitas en un sistema de dos ecuaciones lineales con dos incógnitas.
En este método de solución es importante considerar, que, en un sistema de ecuaciones lineales, las incógnitas tienen el mismo valor para ambas ecuaciones, pero quedan representadas de manera distinta.
¿Qué hacemos?
Comienza el análisis de una situación cotidiana.
Imagina que vas al parque a pasear un rato. La primera ocasión vas con 2 amigos y compras 3 botellas de agua y un coctel de frutas en el kiosco del parque. La cuenta asciende a $125.

Después, vas en pareja y compras 2 botellas de agua y 2 cocteles de frutas. En esta ocasión, se pagan $110.

Se considera que el precio es la suma de cada producto. Y aunque no se sabe cuánto cuesta cada producto por separado, se tienen los suficientes elementos para calcularlo. En ambas ocasiones, los productos conservaron su precio y presentación.
En el primer caso, 3 botellas de agua más 1 coctel de frutas cuestan $125.
En la traducción algebraica, la expresión “3b” representa el costo de las 3 botellas de agua más “c”, el valor del coctel de frutas, igual a 125.
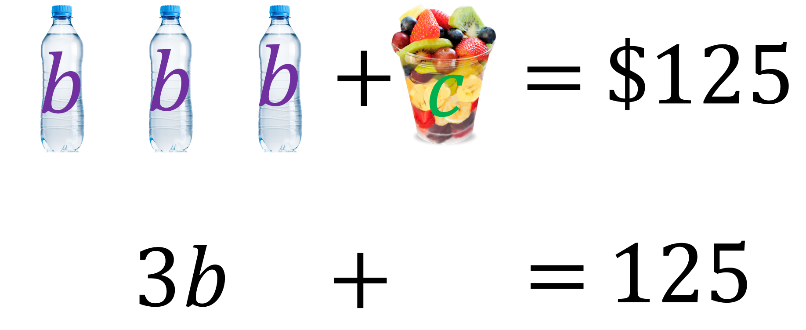
En el segundo caso, 2 botellas de agua más 2 palomitas cuestan $110.
En la traducción algebraica se tiene “2b” para el valor de las dos botellas de agua más “2c”, el costo de dos cocteles de frutas, igual a 110.
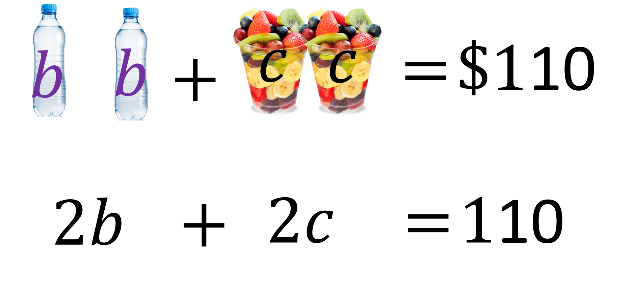
En este caso se aprovecha que, se tiene un único coctel de frutas para calcular su valor.
El costo de este coctel es igual al total de la compra menos el valor de las 3 botellas de agua. Así, el valor de un coctel de frutas se representa como “c” igual a 125 pesos menos “3b”.
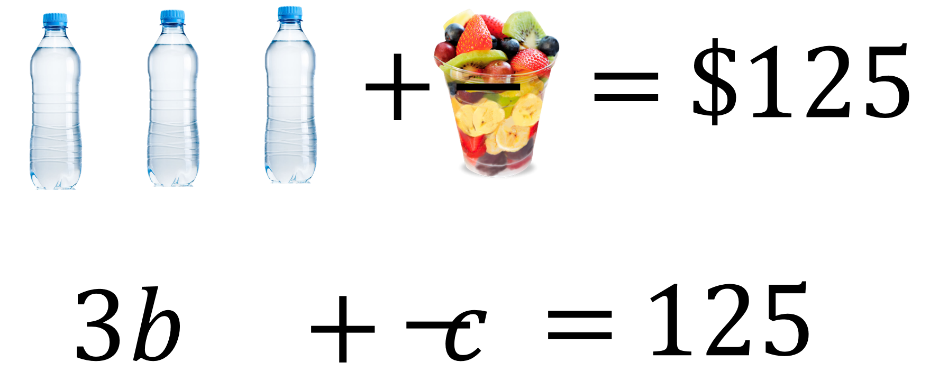
Para el segundo caso, el precio de dos cocteles es el costo total menos el valor de dos botellas de agua.
Si se representa de forma algebraica: “2c” igual a 110 menos “2b”.

Y si ése es el costo de dos cocteles de frutas, uno de estos sólo costará la mitad. Es decir, 55 menos el valor de una botella de agua.
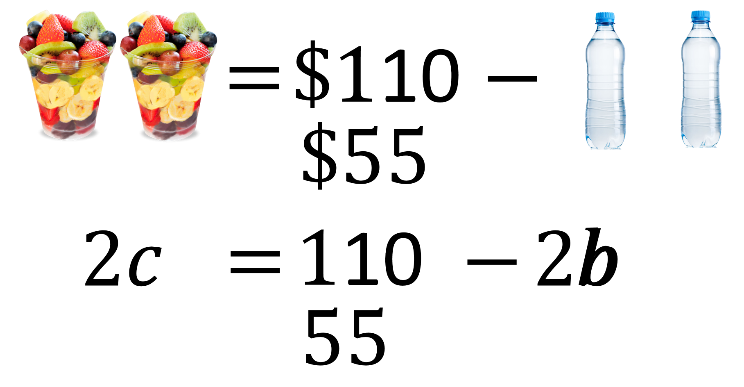
Ahora se tienen las condiciones necesarias para usar el método de igualación.
Ya se tienen dos expresiones para una misma incógnita: el valor de un coctel de frutas.
Se tiene que “c” es igual a 55 menos “b”, y también es igual a 125 menos “3b”.
Entonces, se hace una igualdad con 55 pesos menos el valor de una botella de agua, que es equivalente a 125 pesos menos el valor de 3 botellas de agua.

De esta manera ya se tiene una igualdad en la que sólo está involucrada una incógnita a la vez. Pero ¿cuánto vale una botella de agua?
Analizando la igualdad:
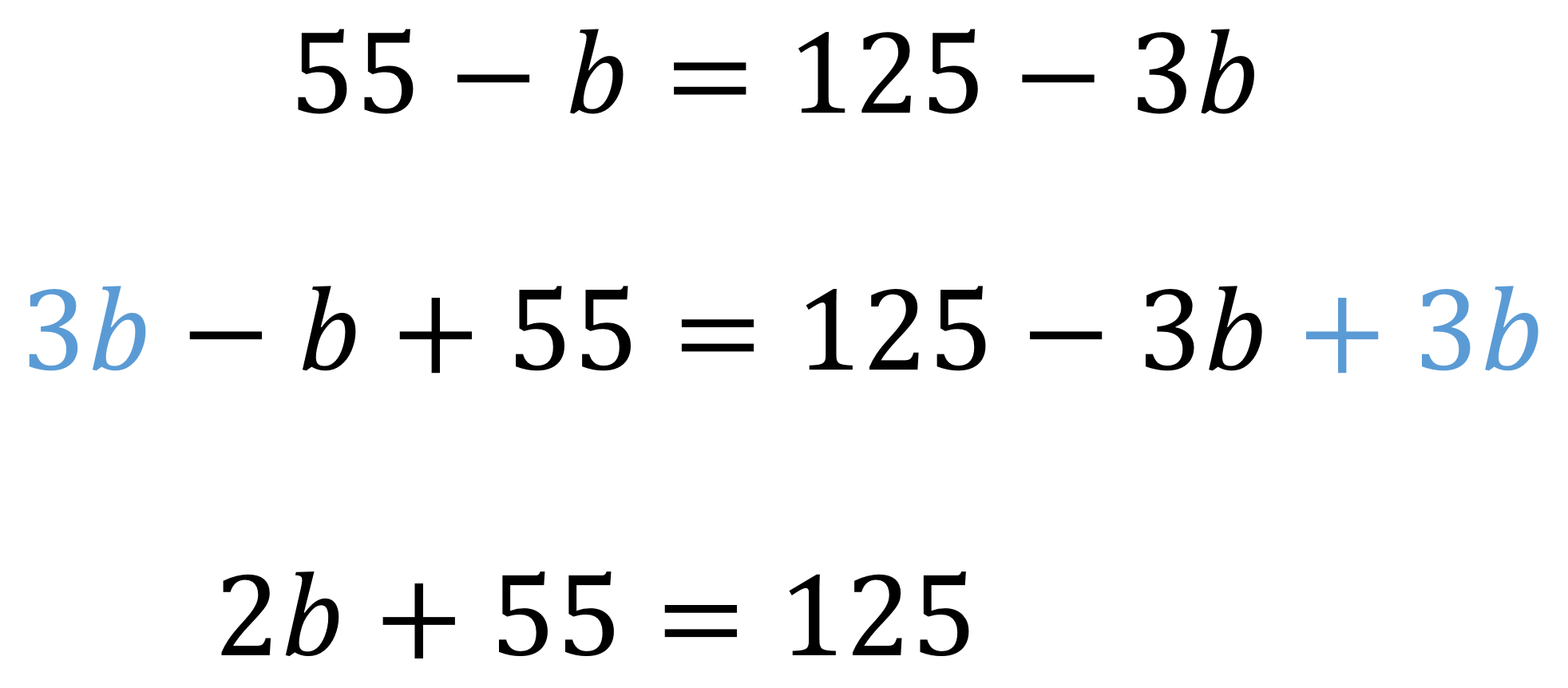
Se resta 55 en ambos lados de la igualdad y se obtiene:

Y si 2 botellas de agua valen 70 pesos, una sola botella de agua vale 35 pesos.
Se tiene el valor de una botella de agua y a partir de este, se calcula el valor de los cocteles. Para ello, se escoge una de las dos expresiones ya despejadas.
“c” igual a 55 menos “b”
o la segunda equivalencia
“c” igual a 125 menos “3b”
En cualquiera de ellas se obtiene el mismo resultado.
Al escoger la primera igualdad y sustituir el valor de la botella de agua, 55 pesos menos 35 pesos, el coctel de frutas vale 20 pesos.

Si se escoge la segunda igualdad, al sustituir el valor de la botella de agua, 125 pesos menos tres botellas de agua de 35 pesos, es igual a 125 menos 105; el coctel de frutas vale 20 pesos, que coincide con el primer cálculo.
De esta manera, se sabe el valor de cada producto de forma independiente: Las botellas de agua cuestan 35 pesos y el coctel de frutas 20 pesos.

Para la segunda situación que trabajarás, el contexto es una función de teatro a la que asistieron 270 personas.
Se recaudaron en total 24,800 pesos
Si los boletos de estudiante cuestan 80 pesos y los boletos para público en general cuestan 100 pesos.
¿Cuántos boletos de estudiante y cuántos de público general se vendieron?
El sistema de ecuaciones asociado a este problema es el siguiente:
Según los datos, el total de estudiantes “x”, más el público en general “y”, es en total 270 personas.
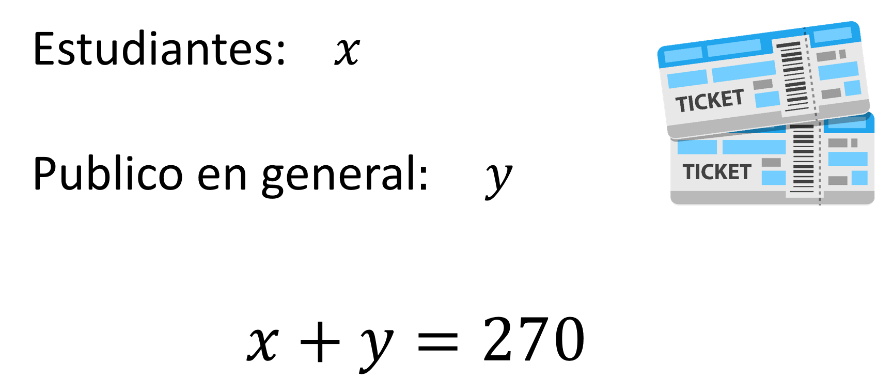
Los boletos de estudiante valen 80 pesos y asistieron “x” número de personas.
Con relación a los boletos de 100 pesos, asistieron “y” número de personas y el ingreso total es de 24,800 pesos.

Ya se tiene el sistema de ecuaciones que describe la situación. Para usar el método de igualación, se despeja la misma incógnita en ambas igualdades.
Se escoge la incógnita “y”, que representa el número de personas que pagaron el boleto general de la obra.
En la primera expresión: “x” más “y” igual a 270, se despeja la incógnita “y”.
Se resta “x” en ambos lados de la igualdad y se obtiene: “y” igual a 270 menos “x”.
En la segunda ecuación:
“80x” más “100y”, igual a 24,800.
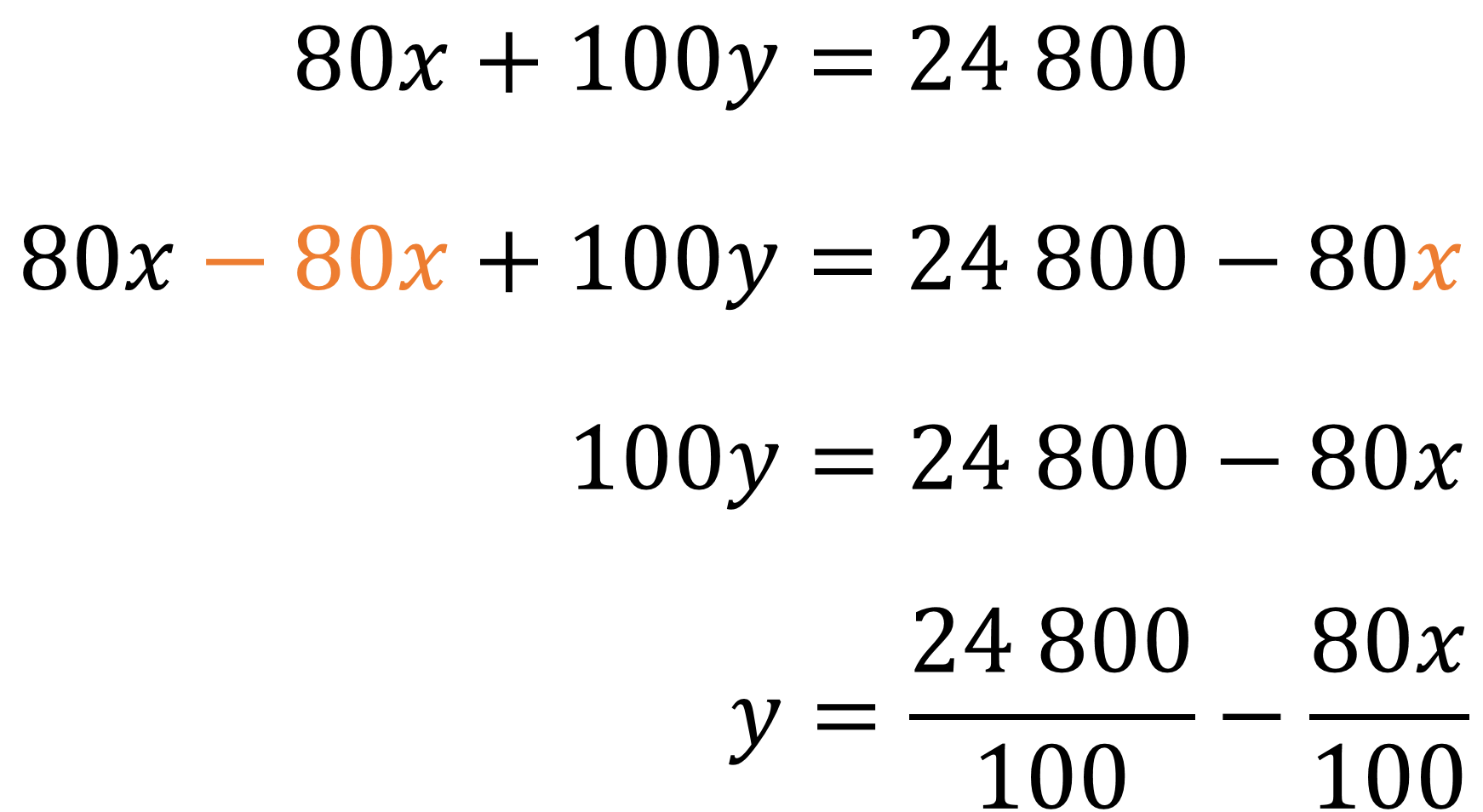
Se resta “80x” en ambos lados de la igualdad para obtener que “100y” es igual a 24,800 menos 80x.
Y se divide toda la expresión entre 100, teniendo como resultado: “y” igual a 24,800 entre 100 menos “80x” entre 100.
Para agilizar el cálculo, se reducen las fracciones a su mínima expresión. Así 24,800 centésimos es igual a 248, y 80 centésimos de “x” es igual a 8 décimos de “x”, que también es equivalente a 4 quintos de “x”.
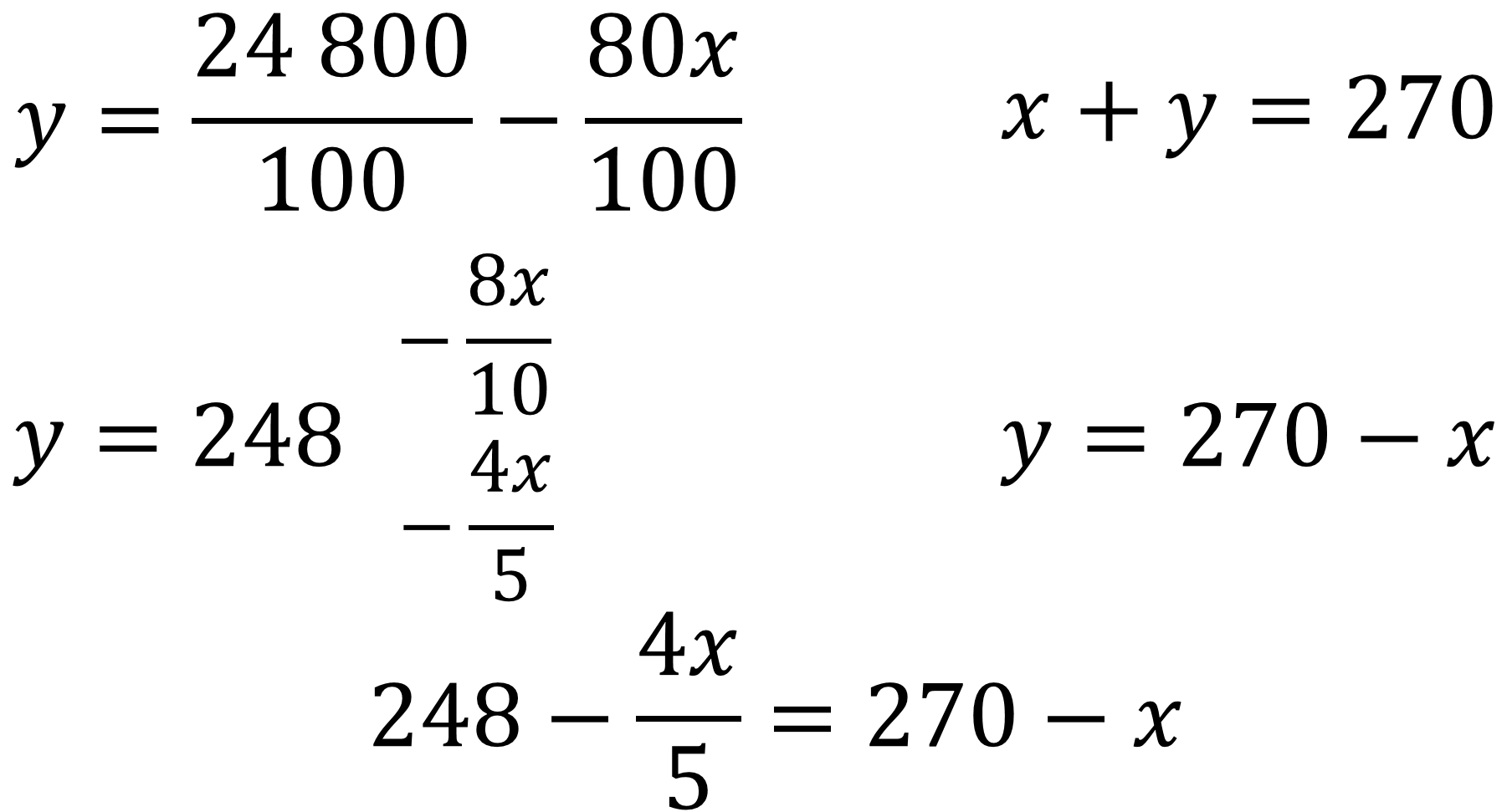
De este modo, ya se tiene despejada la misma incógnita en ambas ecuaciones.
Entonces, se tiene que 248 menos 4 quintos de “x” es equivalente a 270 menos “x”.
Se suma “x” en ambos lados de la igualdad y se obtiene que “x” menos 4 quintos de “x” más 248 es igual 270 menos “x” mas “x”.
Al reducir términos semejantes, para los términos “x” menos 4 quintos de “x”, se puede sustituir un entero por su equivalente 5 quintos.
Y queda, 5 quintos de “x” menos 4 quintos es igual a un quinto de “x”, y en el segundo miembro de la igualdad, “x” menos “x” es igual a cero.
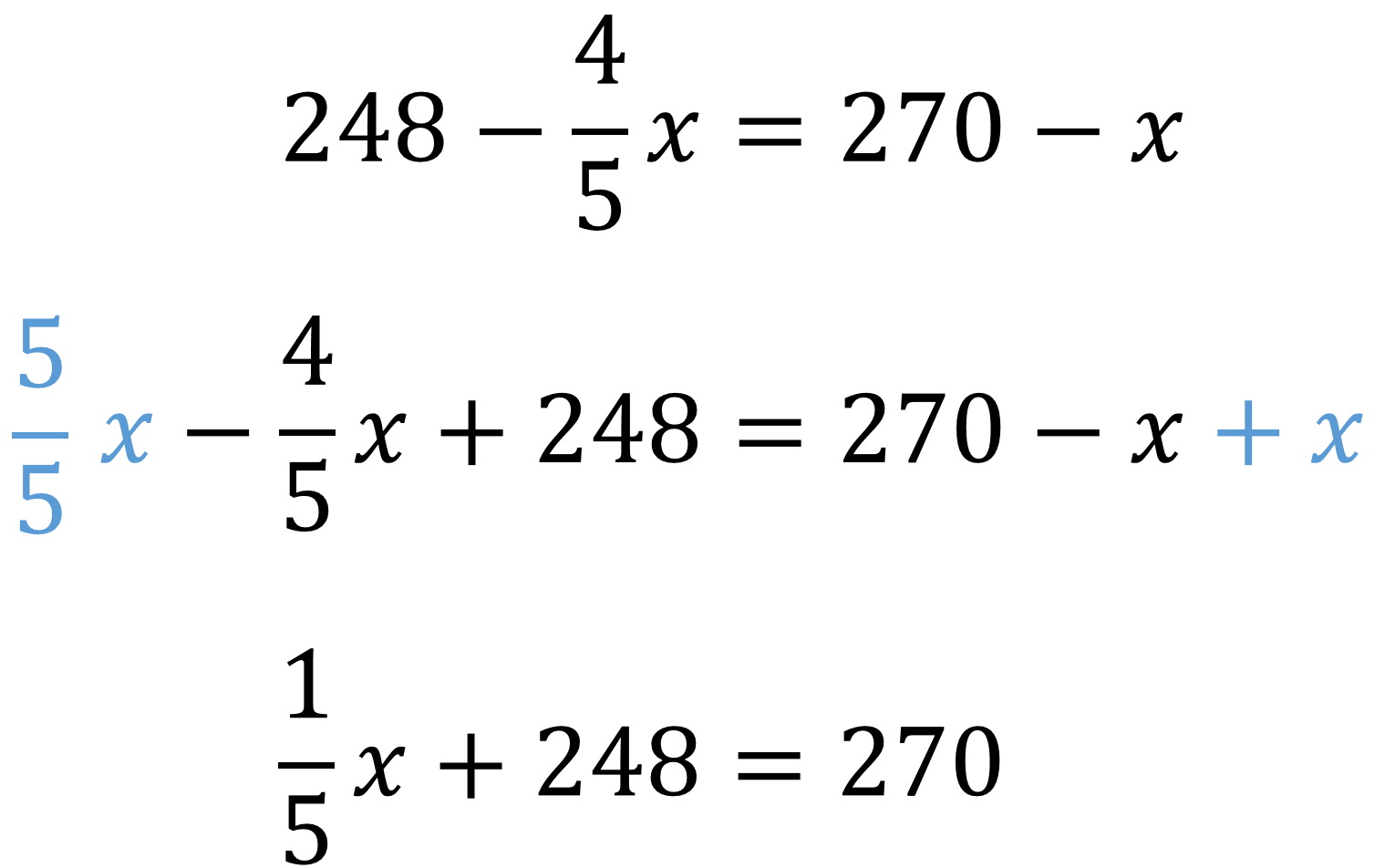
Después, se restan 248 en ambos lados de la igualdad; en el lado izquierdo 248 menos 248 es igual a cero, y del lado derecho 270 menos 248 es igual a 22.
Y para finalizar, si un quinto de “x” es igual a 22, entonces el valor de “x” es cinco veces 22, que es igual a 110.
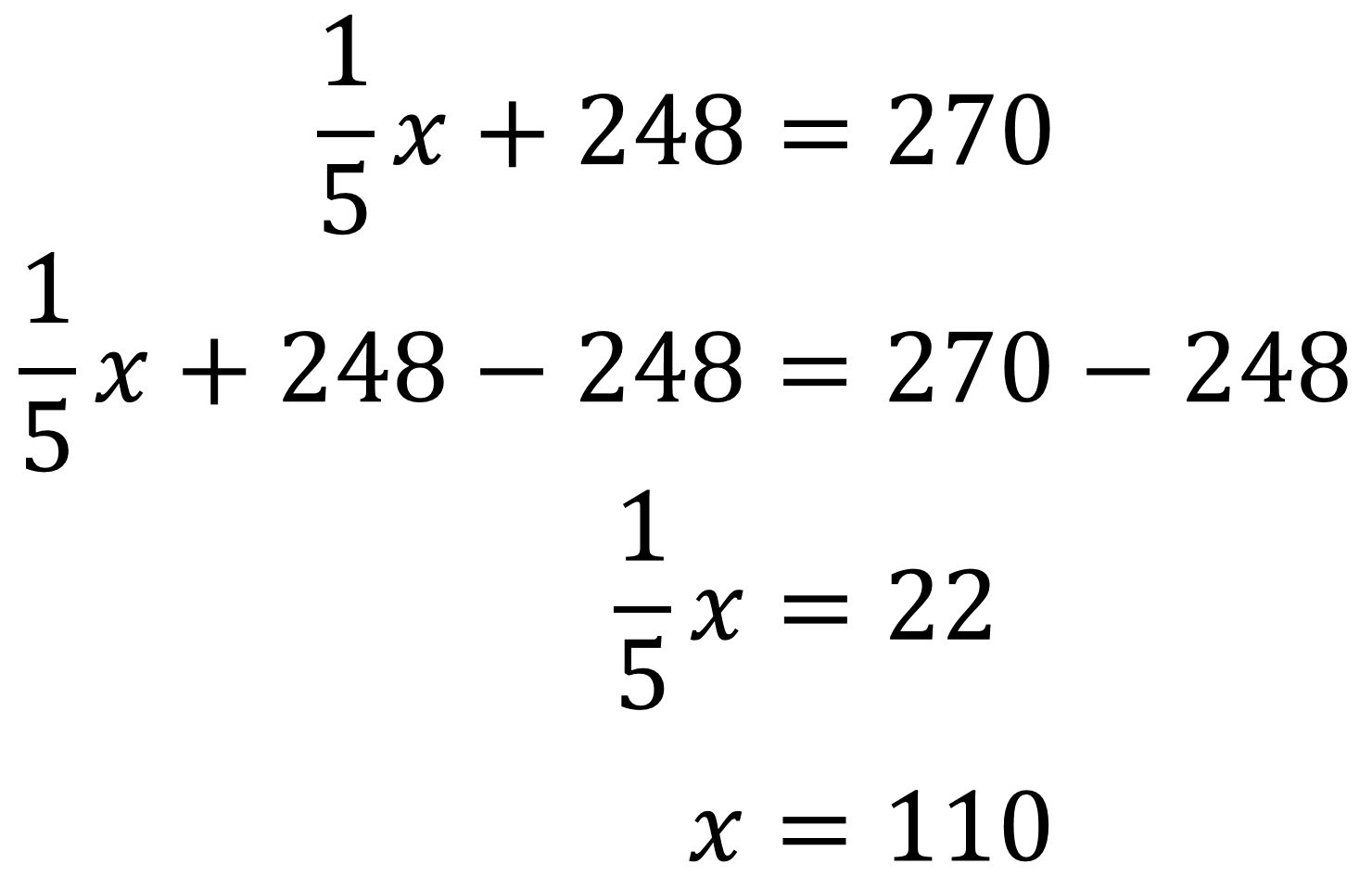
Con el valor de “x” igual a 110 se sabe que fueron 110 boletos para estudiantes los que se vendieron en la taquilla del teatro.
Entonces, para completar las 270 entradas de ese día, se compraron 160 boletos de entrada general.
Para comprobar los valores obtenidos, se sustituyen en la expresión del problema.
La venta de 110 boletos de estudiante, más 160 boletos de entrada general, coincide con las 270 entradas vendidas ese día.
Después, se comprueba que el dinero recaudado por la venta de 110 boletos de 80 pesos, más 160 boletos de 100 pesos, deben de sumar 24,800 pesos.

110 boletos por 80 pesos cada uno, es igual a 8,800 pesos.
160 boletos por 100 pesos de cada uno, es igual a 16,000 pesos.
La suma de 8,800 pesos de los boletos de estudiante más 16,000 pesos, de los boletos de entrada general, es igual a los 24,800 pesos recaudados ese día.

Se lograron encontrar las incógnitas en dos diferentes situaciones donde los datos permitieron usar un sistema de dos ecuaciones lineales con dos incógnitas. Además, en cada situación planteada, el sistema de ecuaciones tenía una única solución.
A continuación, se analizarán dos sistemas en donde no hay una solución o, por el contrario, existen múltiples soluciones que, al resolverlos con el método de igualación, se presentan resultados característicos.
En el sistema: “2x” menos “3y” igual a cero, y “4x” menos “6y” igual a 9.
Se despeja la incógnita “x” de ambas ecuaciones, y se obtiene que en la primera:
“x” es igual a “3y” entre 2
En la segunda ecuación:
“x” es igual a “6y” más 9, todo dividido entre 4.
Por lo tanto, “3y” sobre 2 debe ser igual a la cuarta parte de la suma de “6y” más 9.
Para simplificar la expresión, se multiplican ambos lados de la igualdad por 4, que es el mínimo común múltiplo de los denominadores. Tras realizar las operaciones, se obtiene 2 que multiplica a “3y”, igual a “6y” más 9.

El resultado de las multiplicaciones es “6y”, igual “6y” más 9.
Desde este punto, ya se puede observar que la expresión no es una igualdad, porque 6 multiplicado por cualquier número, no puede ser igual a 6 multiplicado por el mismo número, y todavía sumarle 9 unidades más.
Pero se sigue para conocer la resolución de la situación planteada.
Si se restan “6y” en ambos lados de la igualdad, se obtiene “6y” menos “6y” es igual a 9.
Operando, “6y” menos “6y” es igual a cero, y cero no es igual a 9.
Cuando sucede este tipo de situación, se dice que el sistema no es compatible. Es decir, que no tiene solución.
El otro caso se analiza con el siguiente sistema de ecuaciones:
“2x” más “3y” es igual a 6, con
“4x” más “6y”, es igual a 12.
Se despeja el valor de la incógnita “x” en ambas ecuaciones.
Para la primera ecuación, “x” es igual a un medio de la suma de “3y” negativo más 6.
En la segunda ecuación, “x” es igual a la cuarta parte de la suma de “6y” negativo más 12.
Entonces, se tiene que la mitad de la suma “3y” negativo más 6 es igual a la cuarta parte de la suma de “6y” negativo más 12.
Para simplificar la igualdad, se multiplica por 4, que es el mínimo común múltiplo de los denominadores.
Como resultado de las multiplicaciones, se obtiene: “6y” negativo más 12, es igual a “6y” negativo más 12.
En este punto se puede reconocer que la igualdad tiene los mismos términos, lo que es una identidad. De este modo, se reducen términos semejantes para obtener que cero es igual a cero.
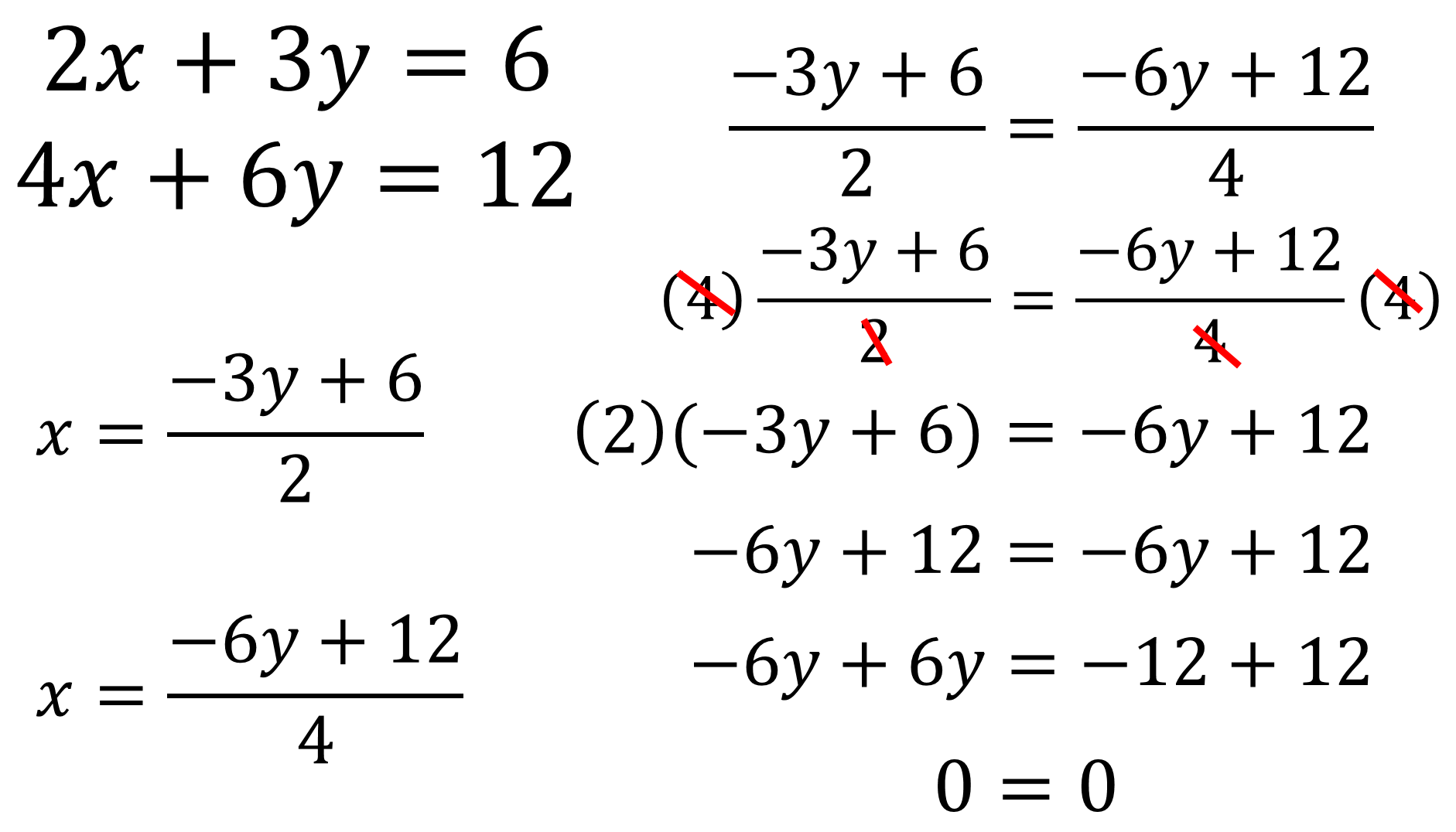
Para este caso, la igualdad es cierta porque cero si es igual a cero, pero no se obtuvo el resultado de la incógnita que se está buscando.
A este tipo de sistemas de ecuaciones se les conoce como “Sistema compatible indeterminado”, es decir, que tiene infinitas soluciones.
Se verifica lo anterior con un par de datos enteros para las incógnitas.
Se asigna el valor de cero a “x” y valor de 2 a “y”; en ambas ecuaciones el resultado es correcto.
2 por cero más 3 por 2 sí es igual a 6
4 por cero más 6 por 2 sí es igual a 12
Y para demostrarlo, se le asigna otro par de valores:
Para “x” igual a 6 y “y” igual a 2 negativo, se tiene 2 por 6 más 3 por 2 negativo, que es igual a 12 menos 6, igual a 6.
En la segunda ecuación:
4 por 6 más 6 por 2 negativo, es igual a 24, menos 12 es igual a 12
Y así como se han empleado estos resultados para “x” y “y”, existen una infinidad de resultados, pero no cualquier combinación, que cumplen con las dos ecuaciones al mismo tiempo.
Después de analizar los casos anteriores, en donde el sistema no tiene solución o existen infinitas soluciones, se estudia una situación que implica el planteamiento de un sistema de ecuaciones en donde también se expresa una ecuación cuadrática.
¿Cuáles son las dimensiones de un terreno rectangular cuyo perímetro es 50 metros y de área cubre 156 metros cuadrados?
Al ser un terreno rectangular se tienen únicamente 2 medidas, el largo y el ancho del terreno que no son iguales, de lo contrario sería un cuadrado.
El perímetro es igual a la suma de todos sus lados, y se tiene en el esquema:
“x” más “y” más “x” más “y” igual a 50 metros.

Al agrupar términos semejantes, se obtiene “2x” más “2y”, igual a 50 metros. Esta expresión representa el perímetro.
El área del rectángulo se obtiene multiplicando el valor del largo “x” por el ancho “y”, que es igual a 156 metros cuadrados.
De esta forma, ya se tienen expresadas dos ecuaciones con dos incógnitas.
Se despeja “x” de la primera ecuación de la que se obtiene “x” igual a 25 menos “y”.
Mientras que al despejar “x” de la segunda ecuación, se obtiene “x” es igual a 156 entre “y”.
Es así como se obtiene la igualdad:
25 menos “y” es igual a 156 entre “y”.
Se comienza a operar la igualdad, multiplicando ambos miembros de la igualdad por “y” para eliminar el denominador, se debe considerar a y diferente de cero.
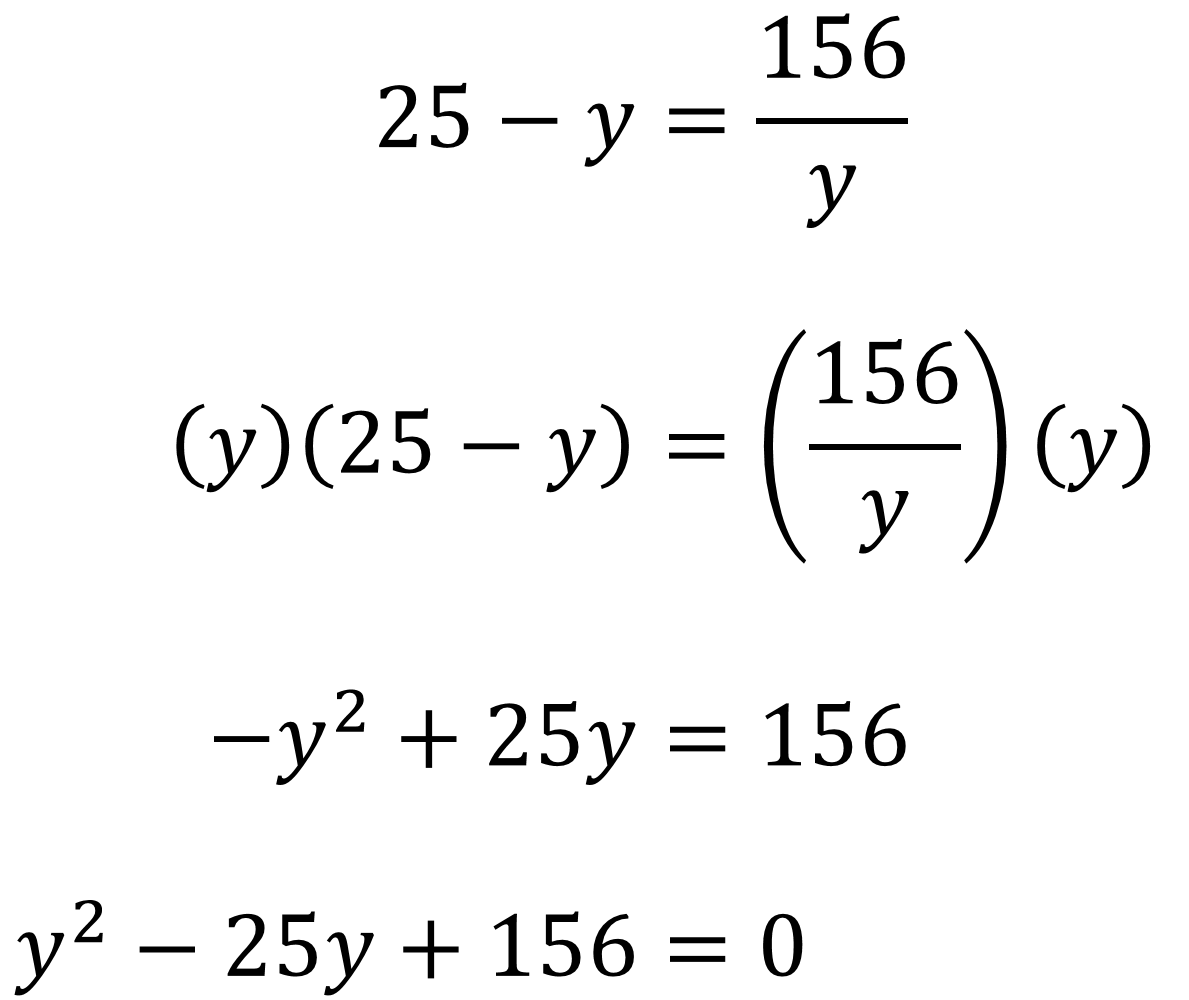
“y” que multiplica a 25 menos “y” es igual a 156 entre “y”, que multiplica a “y”. Realizando la multiplicación se obtiene que: “y” cuadrada negativa más “25y” es igual a 156.
Al igualar la expresión a cero, se multiplica toda la expresión por 1 negativo, para obtener una ecuación de segundo grado.
“y” cuadrada menos “25y” más 156 es igual a cero.
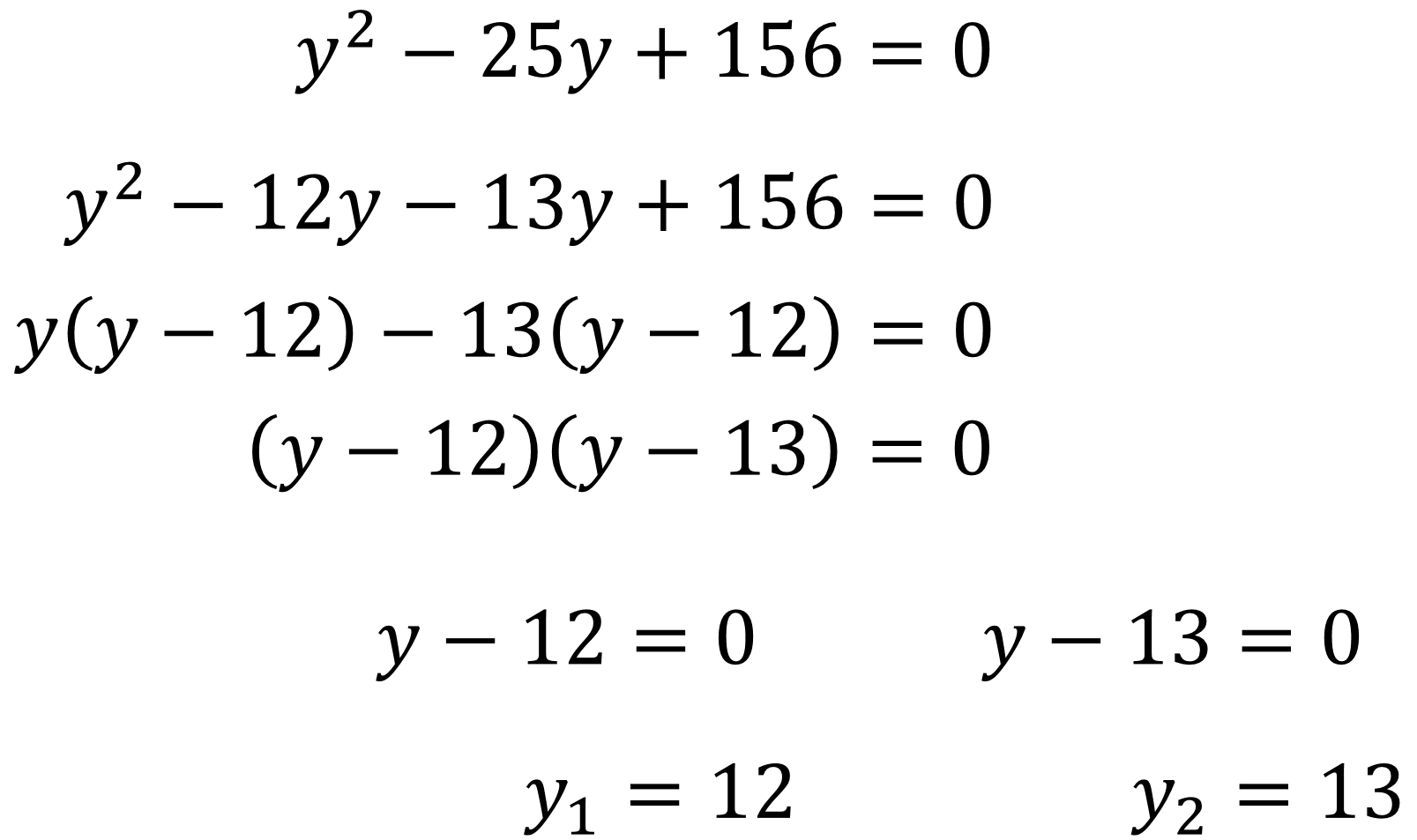
25 negativo se descompone en dos sumandos, de manera que permita factorizar la expresión.
Se elige “12y” negativo y “13y” negativo.
Se calcula el factor común de “y” cuadrada y “12y” negativo, que es “y”, y lo mismo se realiza para “13y” negativo y 156 que es 13.
De este modo se tiene:
“y” que multiplica a “y” menos 12, menos 13, que multiplica a “y” menos 12 es igual a cero.
Se factoriza nuevamente la expresión, ahora utilizando como factor común a “y menos doce) y se obtiene: “y” menos 12 que multiplica a “y” menos 13 es igual a cero.
Se considera ahora que, si el producto de varios factores es igual a cero, entonces al menos uno de los factores es igual a cero.
Esto implica que “y” menos 12 es igual a cero, o “y” menos 13 es igual a cero.
Por lo tanto, las respuestas a estas dos igualdades son: “y” igual a 12, o “y” igual a 13.
Para calcular el valor del lado “x”, se sustituyen los dos valores de “y” en uno de los dos despejes de “x”.
Por ejemplo, en “x” igual a 25 menos “y”.
Para “y uno”, “x” es igual a 25 menos 12, que es igual a 13, y para “y dos”, “x” es igual a 25 menos 13, que es igual a 12.
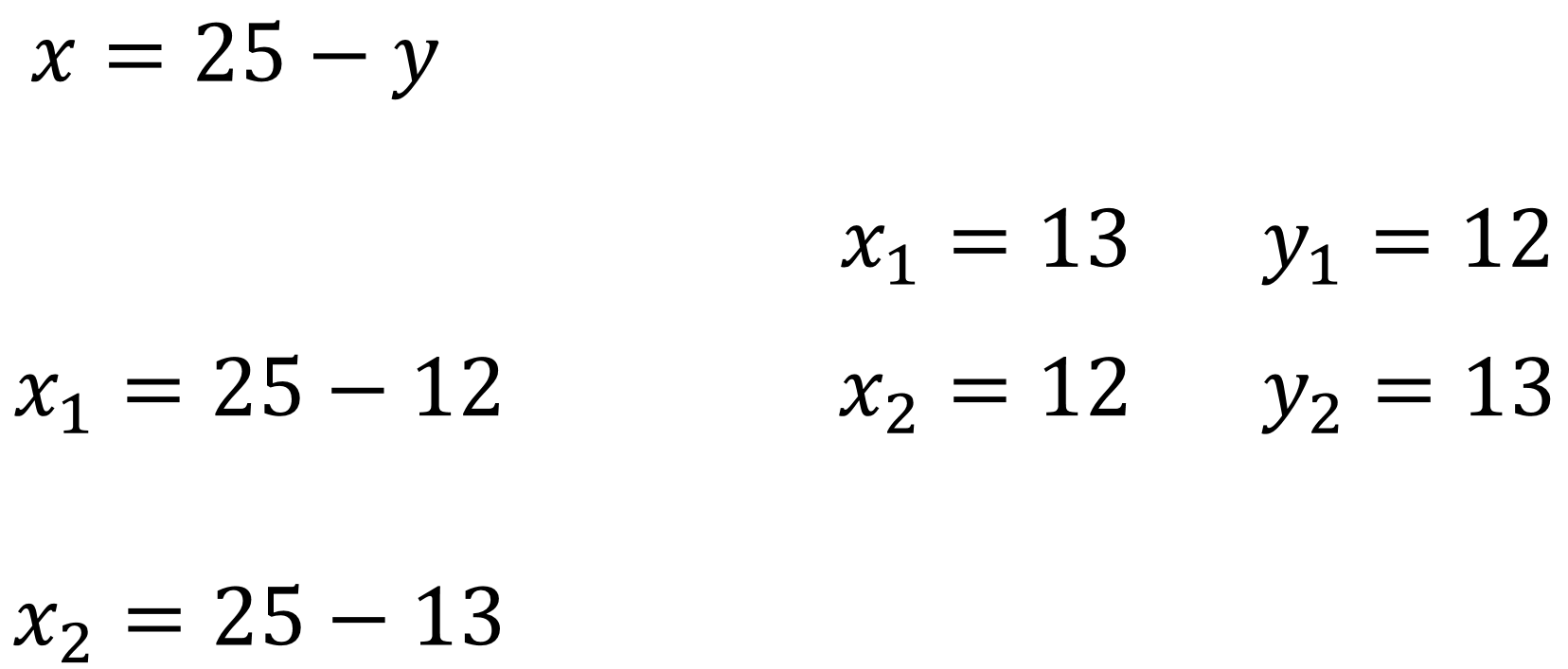
Analizando los resultados, el terreno mide 13 metros de largo por 12 de ancho.
También se puede medir 12 metros de largo por 13 de ancho, que se logra al cambiar la orientación del terreno en el esquema.
En el problema anterior, además de ocupar el método de igualación, también se necesitó de la factorización de una ecuación de segundo grado para poder obtener el resultado.
Como se ha observado durante la sesión, el método de igualación consiste en despejar la misma incógnita de ambas ecuaciones, lo que permite igualar ambas expresiones, (de ahí el nombre del método). Con lo anterior, se genera una ecuación con una incógnita y se evita el manejo de las dos al mismo tiempo.
Para concluir analiza la siguiente situación hasta el punto de la traducción algebraica, y el despeje de la misma incógnita en ambas ecuaciones, para que en casa obtengan la solución utilizando el método de igualación.
Escribe en tu cuaderno los datos necesarios para realizar el ejercicio.
Con dos camiones, cuyas capacidades de carga son respectivamente de 3 y 4 toneladas, se hicieron en total 23 viajes para transportar 80 toneladas de arena. ¿Cuántos viajes realizó cada camión?
Se asigna la variable “x” a la cantidad de viajes que realizó el primer camión; “y” a la cantidad de viajes que realizó el segundo camión. Y se expresan algebraicamente los datos:
La suma de los viajes del primer camión “x”, y el segundo camión “y”, es igual a 23, el total de viajes realizados.
Ahora, se considera que el camión 1 transporta 3 toneladas por cada viaje; la representación algebraica es 3 (toneladas), que multiplica al número de viajes “x”.
Para el camión número 2, cada viaje lleva una carga de 4 toneladas; la representación algebraica es 4 que multiplica al número de viajes “y”.
Finalmente, la suma de la cantidad de arena que transportó el camión 1 (“3x”) más la cantidad de arena que transportó el camión 2 (“4y”) es igual a las 80 toneladas en total.
Se despeja una de las 2 incógnitas en ambas expresiones; para esta se escoge la “y”.
En la expresión “x” más “y” igual a 23 se resta el valor de “x” de ambos lados de la igualdad, y se obtiene que “y” es igual a 23 menos el valor de “x”.
En la segunda expresión, “3x” más “4y” igual a 80, se resta “3x” en ambos lados de la igualdad. Después, se divide entre 4 para obtener que “y” es igual a la cuarta parte de 80 menos “3x”.
Y se aplica el método de igualación para resolver la pregunta: ¿Cuántos viajes realizó cada camión?
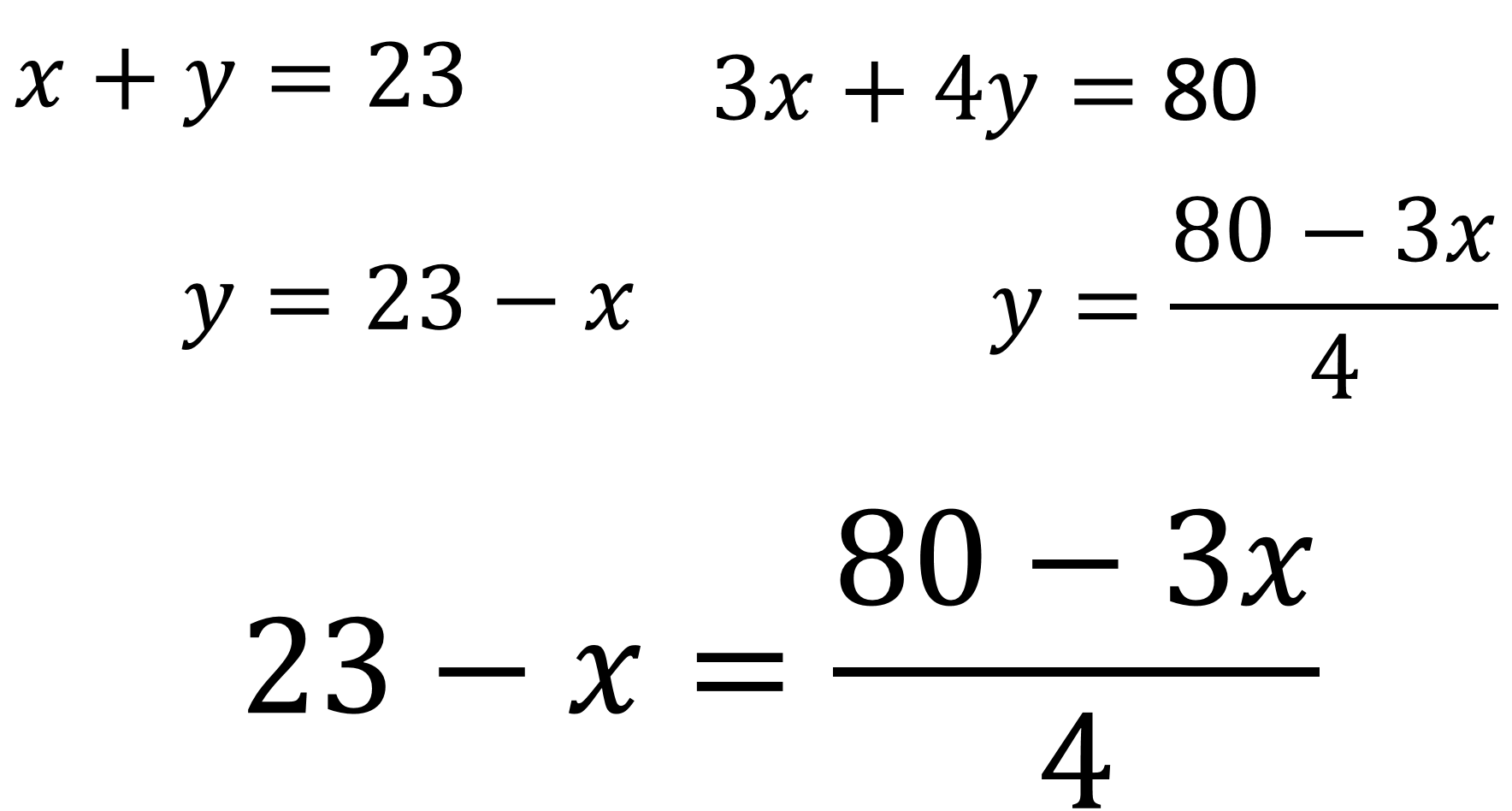
Para ejercicios como los anteriores, existe varios métodos de solución; el método de igualación es el más viable cuando el coeficiente de alguna incógnita es 1, lo que favorece mucho el proceso.
El reto de hoy:
Busca ejercicios o problemas ya resueltos en tu libro del año anterior para repetirlos con el método de igualación, y así verificar cómo se obtiene el mismo resultado con este método.
Y para resolver dudas o ejercitar lo aprendido, te puedes apoyar en tu libro de texto.
¡Buen trabajo!
Gracias por tu esfuerzo.





Login to join the discussion