Secciones de corte

Secciones de corte

Aprendizaje esperado: resuelve problemas que implican calcular el volumen de cilindros y conos o cualquiera de las variables que intervienen en las fórmulas que se utilicen. Anticipa cómo cambia el volumen al aumentar o disminuir alguna de las dimensiones.

Énfasis: dar sentido y significado a las secciones de corte de cilindros y conos.

¿Qué vamos a aprender?

A veces, las personas usan las matemáticas sin pensarlo, e incluso se practican en situaciones insospechadas.

Durante esta sesión, se estudian las secciones de corte de cilindros y conos y algunos ejemplos de su utilidad en la vida cotidiana.

El material que necesitas es tu cuaderno de matemáticas, lápiz y goma. Anota lo que consideres importante, así como las dudas que surjan durante el desarrollo de la sesión.

Conoce primero el cilindro.

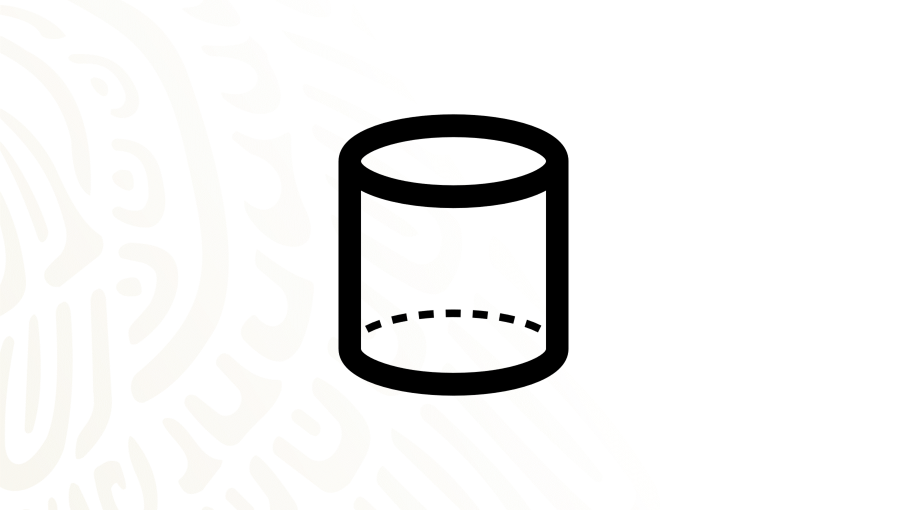
Este es un cuerpo geométrico, por lo que tiene volumen.

El cilindro es considerado un cuerpo de revolución porque se forma al girar una figura plana sobre uno de sus ejes. En su caso, un rectángulo.

Otros cuerpos de revolución son el cono y la esfera.

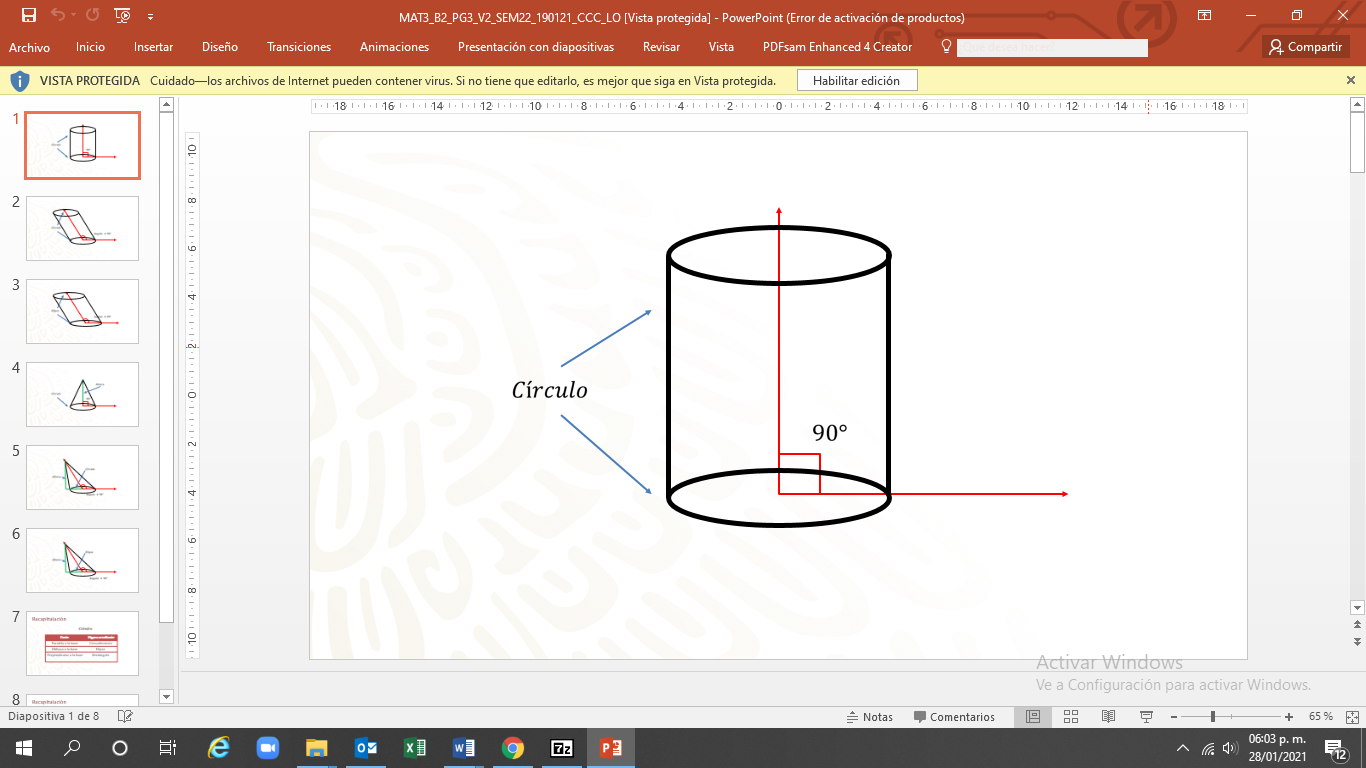
Y los cilindros se clasifican según el ángulo formado entre sus bases y su eje: en el “cilindro recto” las bases son circulares, y el ángulo entre la base y el eje es de 90°.

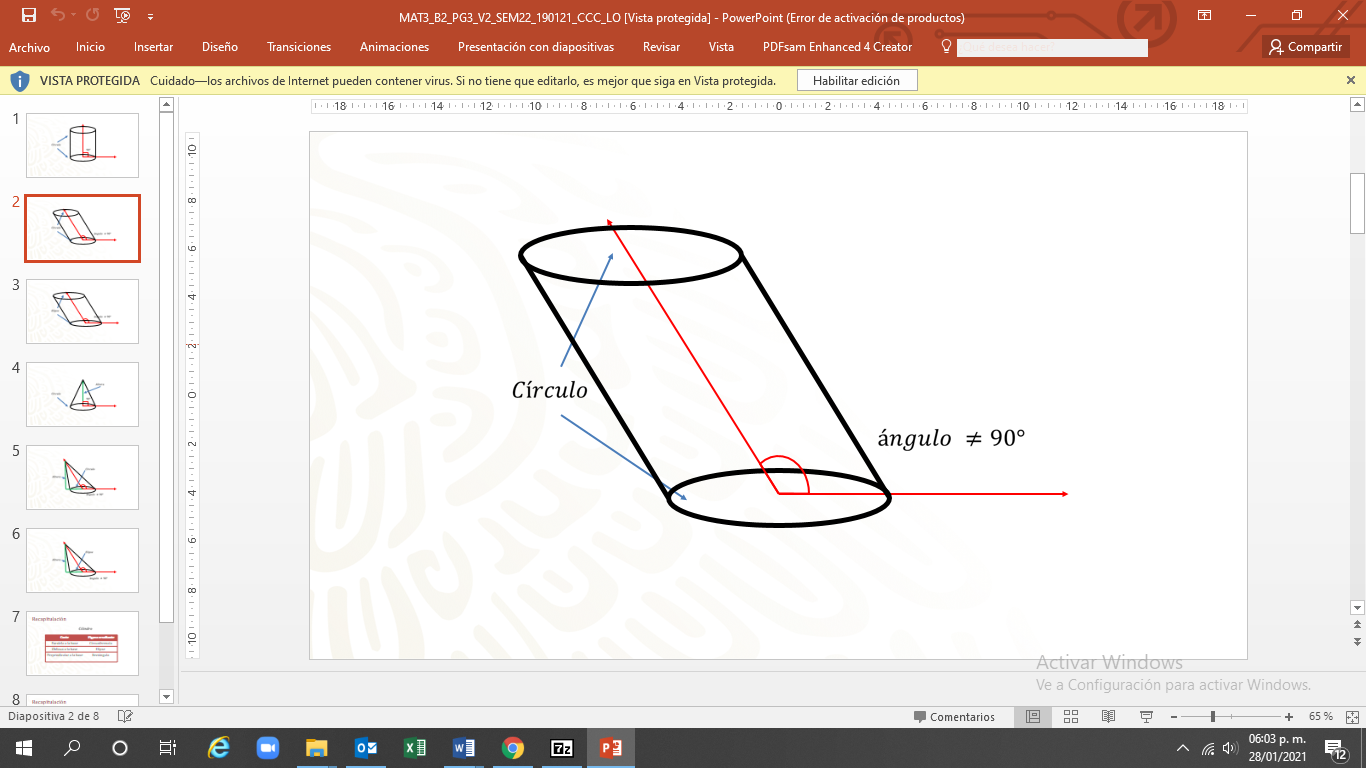
El “cilindro oblicuo de base circular” es aquel cuya base es una circunferencia, y el ángulo entre la base y el eje no es recto.

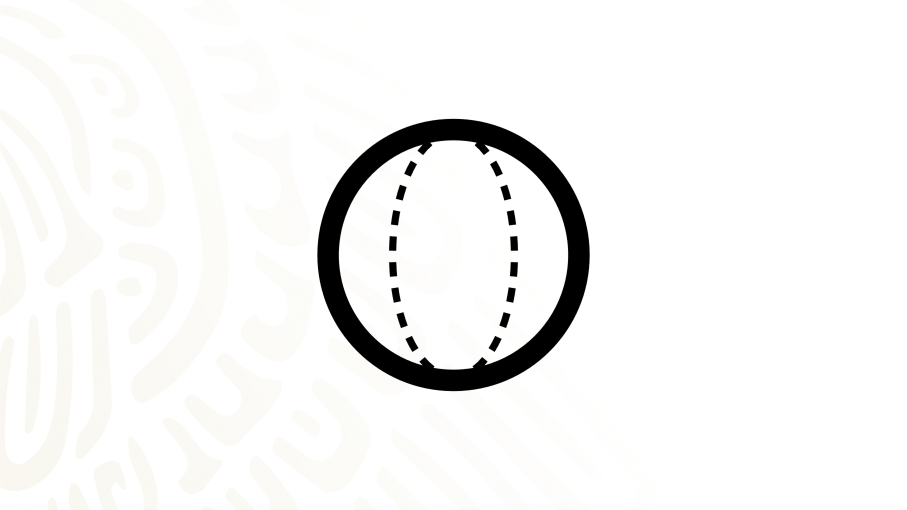
Y el “cilindro oblicuo de base elíptica”, cuya base es una elipse, y el ángulo entre la base y el eje no es recto. Es decir, diferente de 90°.

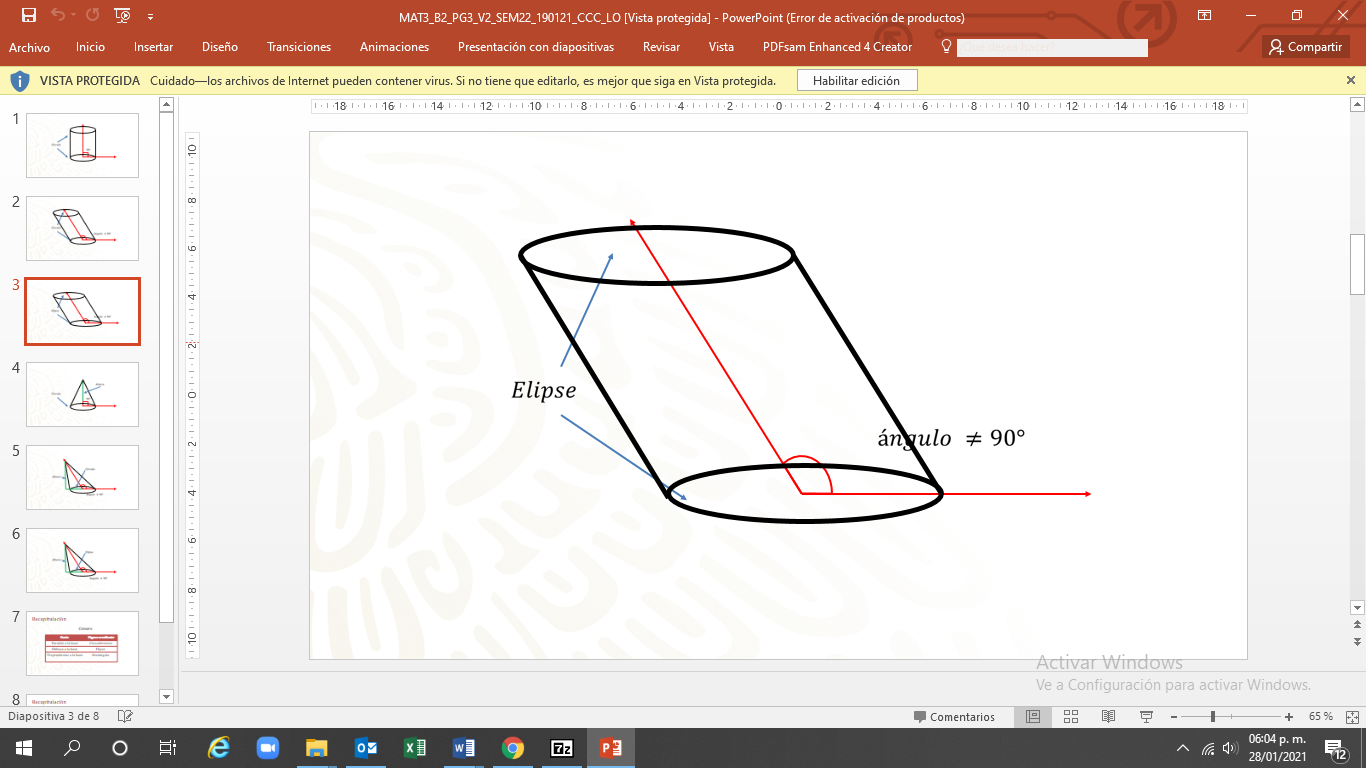
Sin embargo, para el propósito de esta clase sólo se utilizará el cilindro recto.

¿Qué hacemos?

El cilindro se forma por el desplazamiento de un cuadrado o un rectángulo que gira sobre un eje llamado directriz. En este caso, a lo largo de una circunferencia a la que denominamos generatriz.

En la animación se ve cómo un cuadrado que se encuentra en dos dimensiones se desplaza sobre uno de sus ejes —que como ya mencionamos— se le denomina directriz. ¿La reconoces?

1. Video 01
   https://youtu.be/3zy_rnVfZFU
   (del min. 2.48 al 3.04)
   Al girar la animación para verse en tres dimensiones, se observa que en la base existe una circunferencia que describe la generatriz.
   Y si se modifica el tamaño del cuadrado, se cambia la vista a dos dimensiones para que se pueda apreciar este cambio de tamaño del cuadrado —al que se le agregan dos unidades—, y se repite el proceso anterior.
   Un dato interesante del cilindro es que se usa en distintos objetos: botes de basura, tanques de gas, contenedores de agua, envases plásticos, bocinas USB —y si se modifican las bases—, se encuentra hasta en un lápiz o un bolígrafo, útiles para tu cotidiano.
   En la animación del lado derecho están la figura y los puntos de referencia del plano, vistos desde la parte superior del cilindro en dos dimensiones. Esto con la finalidad de que se observe con claridad el corte al cuerpo geométrico.
2. Video 02
   https://youtu.be/3zy_rnVfZFU
   (del min. 3.05 al 4.20)
   Del lado izquierdo está el cuerpo geométrico en tres dimensiones con el plano de corte. Se observa desde diferentes ángulos para que, auxiliados por el movimiento de los puntos de referencia, el plano se pueda colocar en horizontal, vertical o de forma inclinada. Esto con la finalidad de que se realicen distintos cortes.
   Y la sección generada se observa del lado derecho de la pantalla.
   La primera sección que se realiza en el cilindro es la que corresponde con el corte paralelo a las bases. Pero ¿qué sucede cuando se corta el cilindro por un plano?
3. Video 03
   https://youtu.be/3zy_rnVfZFU
   (del min. 4.21 al 5.05)
   Estas son el cilindro y la vista en dos dimensiones iguales —al ser vistas desde la parte superior—. Después se gira la vista en tres dimensiones para ubicar el plano —paralelo a las bases—, y no se pierde de vista la parte derecha de la pantalla porque ahí se ve la forma del corte.
   Con la ayuda de los puntos de referencia del plano de corte, se desplaza el mismo hacia la parte superior, uno por uno para hacerlo de la mejor manera.
   Como el plano tiene tres puntos, se mueven a la misma altura, de lo contrario, quedaría inclinado y no en perpendicular.
   El corte está en tres dimensiones, y si se gira la vista es para que se aprecie de mejor manera.
   Del lado derecho está la vista en dos dimensiones que no cambió y, por lo tanto, se conserva. Con esto se deduce que cuando el corte es paralelo a la base, el área de corte es igual a la base: un círculo.
   Si se mueve el plano de corte sobre el mismo cilindro dos unidades más arriba, y se coloca paralelo a la base, ¿por qué no se cambia la forma que proyecta el corte?
   Porque permanece circular: la figura proyectada siempre será una circunferencia con las mismas dimensiones de la base, sin importar la figura del corte.
   Un dato por conocer: cuando el corte al cilindro es paralelo a la base, las secciones obtenidas tienen forma circular. Analiza la segunda actividad.
4. Video 04
   https://youtu.be/3zy_rnVfZFU
   (del min. 5.06 al 6.45)
   Se inicia con la misma vista superior del cilindro. El corte que se hace es oblicuo a las bases, pero sin que el plano las toque. Es decir, sólo sobre el cuerpo del cilindro.
   Se coloca el plano de forma inclinada para evitar que éste toque las bases, ya que el corte cambia la forma esperada.
   El plano ya no toca las bases, y se gira para apreciar su forma. ¿Sabes cómo se llama esta figura?
   Aunque no es muy pronunciada, en la forma se observa que el área circular se pierde al momento que se alarga hacia los lados.
   La figura resultante es conocida como elipse. Entre más inclinado esté el plano, la elipse será más larga.
   Cuando éste se incline más, se cambian de lugar los puntos de referencia. ¿Observas cómo varía la forma de la elipse cuando el corte alcanza la base? Parece que se cortó de tajo.
   Se siguen moviendo los puntos para poder inclinar más el plano, con el objetivo de alargar más la elipse.
   En la vista en tres dimensiones se observa la elipse cortada dentro del cilindro, mientras que del lado derecho se tiene el corte visto en dos dimensiones.
   Finalmente, con la vista lateral del cilindro, se observa el corte inclinado y se brinda información de la altura de la sección.
   Se realizaron dos cortes al cilindro: uno paralelo a la base —el cual da un área circular—, y el segundo un corte oblicuo a las bases sin que éste las toque, resultando el corte en una elipse.
   Continúa con la tercera actividad.
5. Video 05
   https://youtu.be/3zy_rnVfZFU
   (del min. 6.46 al 8.37)
   El corte que se realiza es perpendicular a la base, es decir que el plano de corte y la base forman un ángulo de 90 grados. Para verlo se realiza este corte al centro del cilindro. Como el movimiento de los puntos de referencia es más complicado, se requiere de paciencia al ejecutarlo.
   Se mueve cada uno de los puntos hacia la parte superior, de forma que se coloque verticalmente el plano.
   Si se observa el lado derecho de la pantalla, se nota cómo cambia poco a poco la circunferencia y se transforma en una figura diferente.
   Y aunque este movimiento es complicado, se tiene que lograr. Para asegurarse de que esté bien hecho, se necesita girar la vista en distintas posiciones y ajustar todos los puntos como desees.
   Del lado derecho, la forma circular se pierde y se transforma pasando primero a un trapecio y después a un paralelogramo, que es el objetivo final. Esto ocurre porque el corte no se encuentra totalmente a 90 grados.
   Si se observa, la vista giró en diferentes posiciones para conseguirlo.
   La superficie cambió por un rectángulo que se describe a la perfección en la vista del lado derecho.
   Si se gira la vista en tres dimensiones, se logra encontrar el rectángulo al interior del cilindro. ¿Lo notas?
   Al realizar tres cortes diferentes al cilindro, también se encuentran tres superficies distintas: una circunferencia, una elipse y un rectángulo.
   Pasa al cono: se sabe que existen diferentes tipos de conos y los puedes clasificar según el ángulo formado entre su base y su eje.
   El cono recto: su base es circular, el pie de la altura está en el centro de la base. El ángulo entre la base y el eje es de 90°.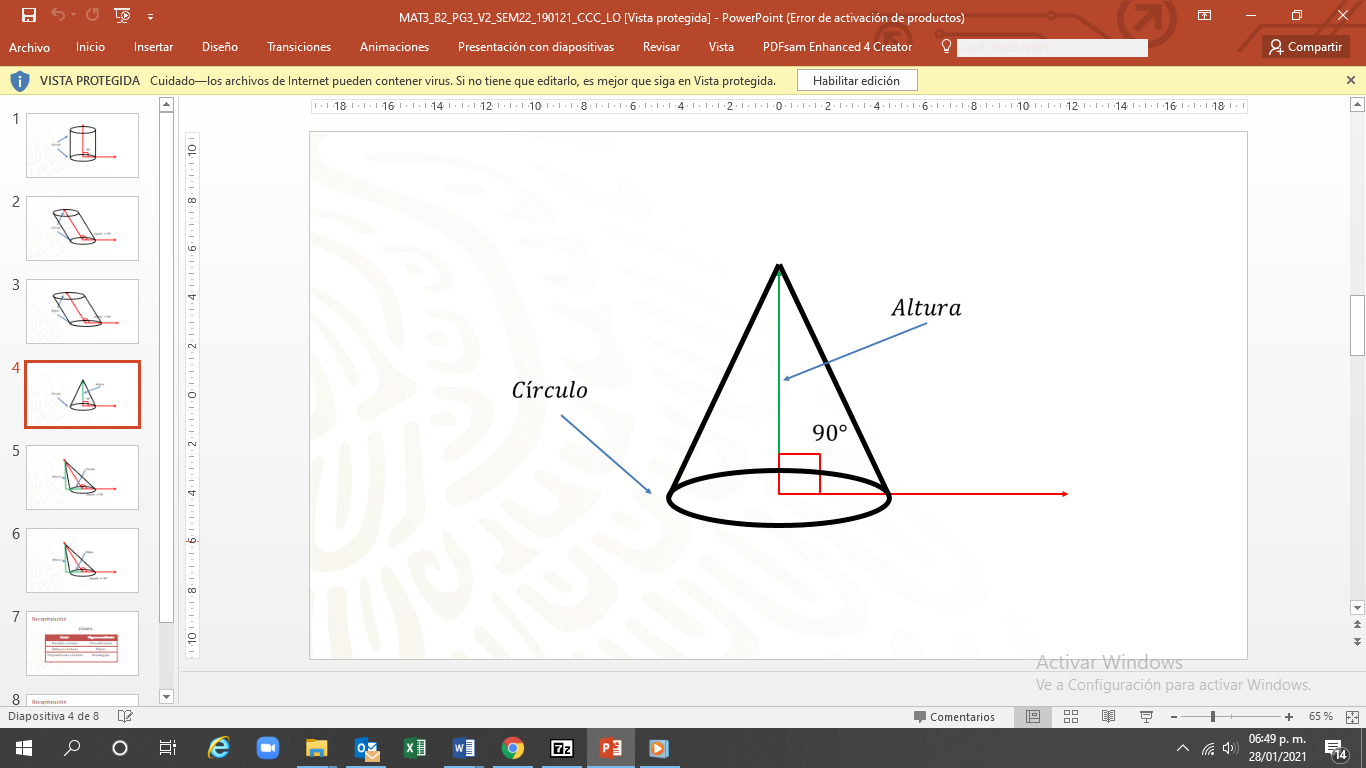
   
   Cono oblicuo de base circular: su base es una circunferencia; el ángulo entre la base y el eje no es recto. La altura no pasa por el centro de la base.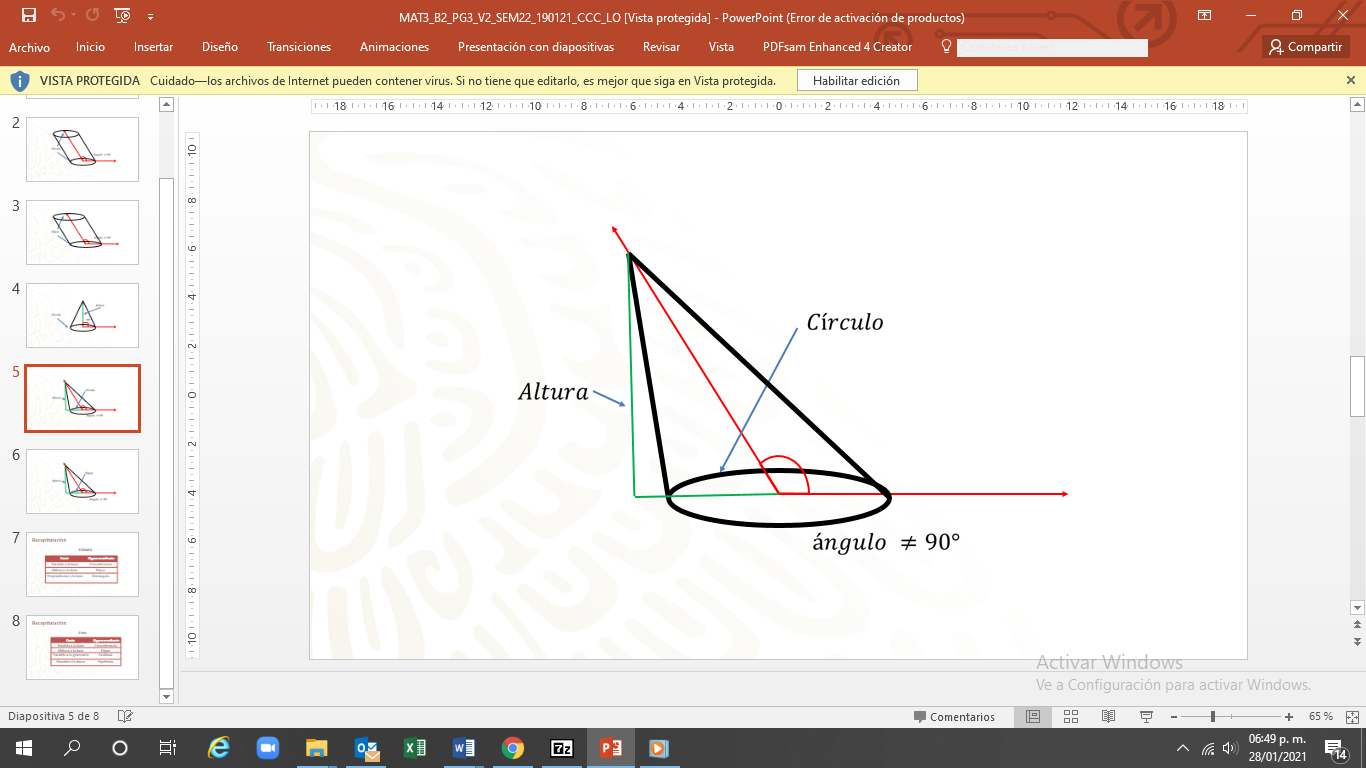
   
   Y cono oblicuo de base elíptica: su base es una elipse; el ángulo entre la base y el eje no es recto, es decir, diferente de 90°. La altura no pasa por el centro de la base.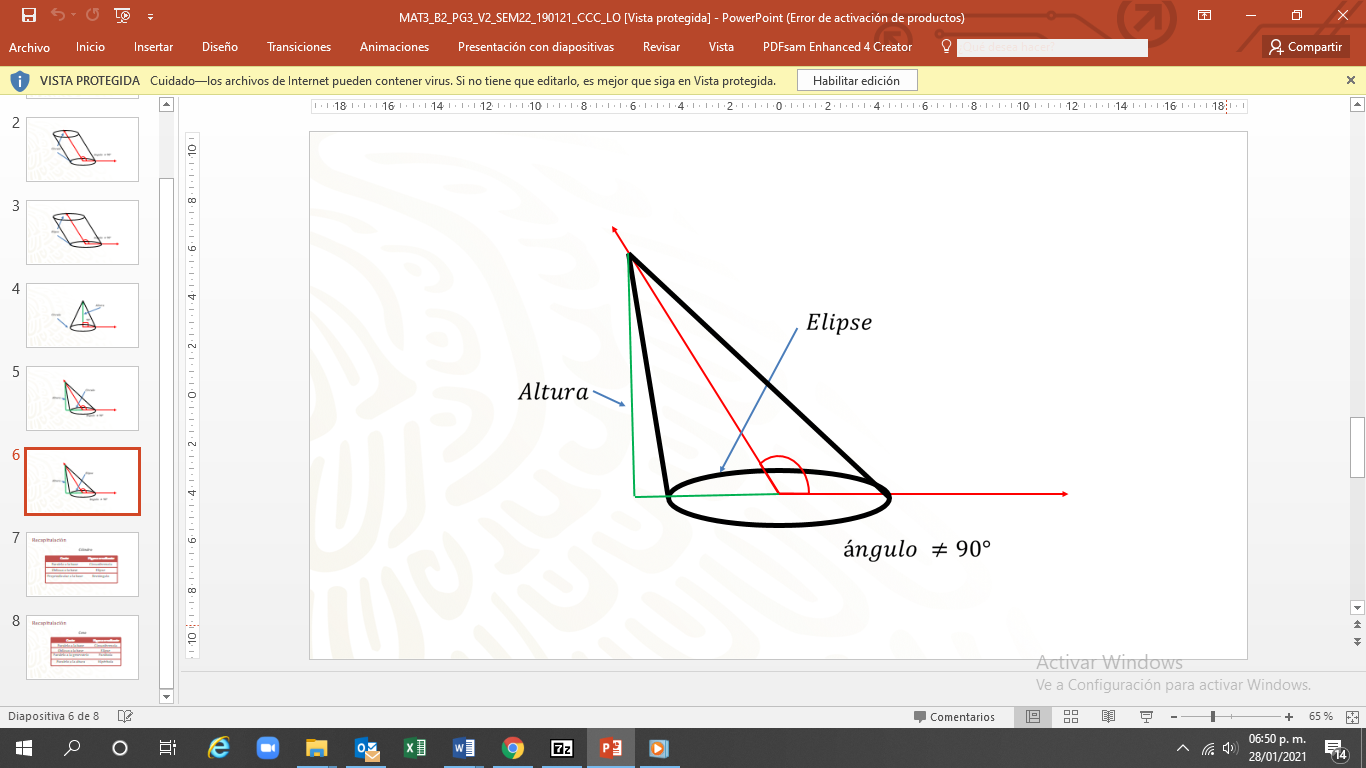
   
6. Video 06
   https://youtu.be/3zy_rnVfZFU
   (del min. 8.38 al 11.21)
   Al cono también se le conoce como un cuerpo de revolución porque se consigue al girar una figura sobre uno de sus ejes.
   Se parte de un triángulo rectángulo que tiene un ángulo de 90 grados. Se gira sobre uno de sus catetos y se ve cómo forma el cono.
   ¿Cuál es la directriz de este cuerpo? El cateto sobre el que gira el triángulo.
   ¿Y la generatriz? La línea que forma el cono al girar la hipotenusa del triángulo rectángulo.
   Al igual que con el cilindro, si el cateto que tiene la función de directriz se amplía —y el cateto que forma el radio del cono le cambias las medidas—, tiende a cambiar el volumen del cono.
   Al igual que se hizo con el cilindro, se realizan algunos cortes al cono, los cuales dan como resultado figuras geométricas —algunas que ya conoces— y otras que tal vez sean nuevas para ti.
7. Video 07
   https://youtu.be/3zy_rnVfZFU
   (del min. 11.23 al 12.27)
   El primer corte que se realiza en el cono es paralelo a la base.
   Se usa la vista en tres dimensiones para mover el plano de corte y colocarlo paralelo a la base inferior mediante los puntos de referencia de éste.
   Es importante que se encuentre totalmente paralelo, pues de otra forma la figura resultante no será la esperada.
   Se gira la figura para asegurarse que el plano esté bien colocado. No pierdas de vista la figura del lado derecho de la pantalla, para que reconozcas los cambios de ésta.
   Aunque esta figura es plana, representa una superficie que le fue seccionada al cono.
   Al compararla en la animación, se ve cómo resulta en una figura de forma circular más pequeña que la base.
   Pero ¿qué pasa si se le corta el paralelo con mayor distancia de la base?
   Para comprobarlo, se mueven los puntos de referencia y se ajusta el plano hacia la parte superior. El resultado es muy similar: una circunferencia —más pequeña que el corte anterior— y por supuesto, más pequeña que la base.
   En el primer corte al cono se encuentra una circunferencia que cambia de tamaño conforme se aleja de la superficie de corte de la base. Y si se inclina el plano con respecto a la base, ¿qué superficie se obtiene?
8. Video 08
   https://youtu.be/3zy_rnVfZFU
   (del min. 12.27 al 14.02)
   Para esta segunda actividad se inclina el plano de corte de acuerdo con la base.
   Es importante que el corte no toque la base ni el vértice del cono, ya que cambiaría la superficie resultante.
   Se debe observar que dentro del cono se forma una elipse —no importa hacia dónde se gire la vista del cuerpo geométrico—. Con esto, es notoria la deformación de la superficie circular en la parte derecha.
   Entre menos inclinado esté el plano, la elipse se transforma en una circunferencia.
   La figura resultante —que representa la superficie cortada por un plano de corte a un cono recto de forma oblicua a la base sin tocarla— es una elipse.
   Sin embargo, el tercer corte al cono da como resultado una curva muy distinta a las demás.
9. Video 09
   https://youtu.be/3zy_rnVfZFU
   (del min. 14.03 al 15.01)
   El corte que se realiza al cono es paralelo a la generatriz. Para lograrlo es necesario que se incline el plano de corte, de tal forma que se encuentre perfectamente paralelo a la generatriz.
   Se mueven los puntos de referencia de tal manera que se inclina el plano. Para hacerlo bien se gira la vista en tres dimensiones de diferentes formas y así tener la mejor perspectiva.
   De este modo se obtiene una curva, resultante de trabajar con ecuaciones, principalmente las de variación cuadrática.
   En la pantalla de la derecha se observa la curva formada por este corte; lo importante es la curva, no la línea recta que la secciona.
   En la parte izquierda se observa que está adentro del cono. ¿Conoces su nombre?
   Esta curva es una parábola, y en la actualidad se emplea para las telecomunicaciones. También se encuentra en las antenas satelitales, en los faros del automóvil, o en la forma curva que tienen los radiotelescopios que envían y reciben señales entre la Tierra y los satélites. Es por ello por lo que las antenas con esta forma llevan el nombre de “antenas parabólicas”.
10. Video 10

https://youtu.be/3zy_rnVfZFU

(del min. 15.02 al 16.23)

Para el último corte se necesitan dos conos. Ambos se generan al prolongar la generatriz del primero de ellos. Estos comparten tanto el vértice como su eje.

Para esto, con el programa de animación se crea primero el otro cono —de forma que se mueva el plano de corte—, y abarque ambos cuerpos geométricos.

El corte por realizar debe ser perpendicular y a la altura de los conos.

Con cuidado se desplaza el plano para ponerlo de forma perpendicular a la base. Mediante cada uno de los puntos de referencia se debe formar un ángulo de 90° entre la base y el plano de corte.

Mientras se realiza esto, se nota que en la parte derecha de la pantalla desaparecieron las figuras. Esto es porque el plano salió de los conos, pero al tocarlos de nueva cuenta se vuelven a aparecer.

En la parte derecha se ven los dos cortes planos que se logran; ambos son simétricos.

En arquitectura, con estas curvas les dan forma a algunos cables que sostienen los puentes. Es muy empleada para darle una forma distinta a las construcciones; se utiliza en algunos tipos de telescopios.

Piensa en un reloj de arena. Los relojes de arena son un ejemplo simple de este tipo de curvas. Se caracterizan porque ambas abren en sentidos contrarios de forma simétrica su nombre es hipérbola.

Pero antes, recapitula lo que aprendiste en esta sesión: primero, el cilindro, que se le hicieron tres cortes.

El primero fue paralelo a la base, y con éste se obtuvo una circunferencia.

El segundo fue oblicuo a la base, y se obtuvo una elipse.

Y el tercero y último corte al cilindro fue perpendicular a la base, y se obtuvo un rectángulo.

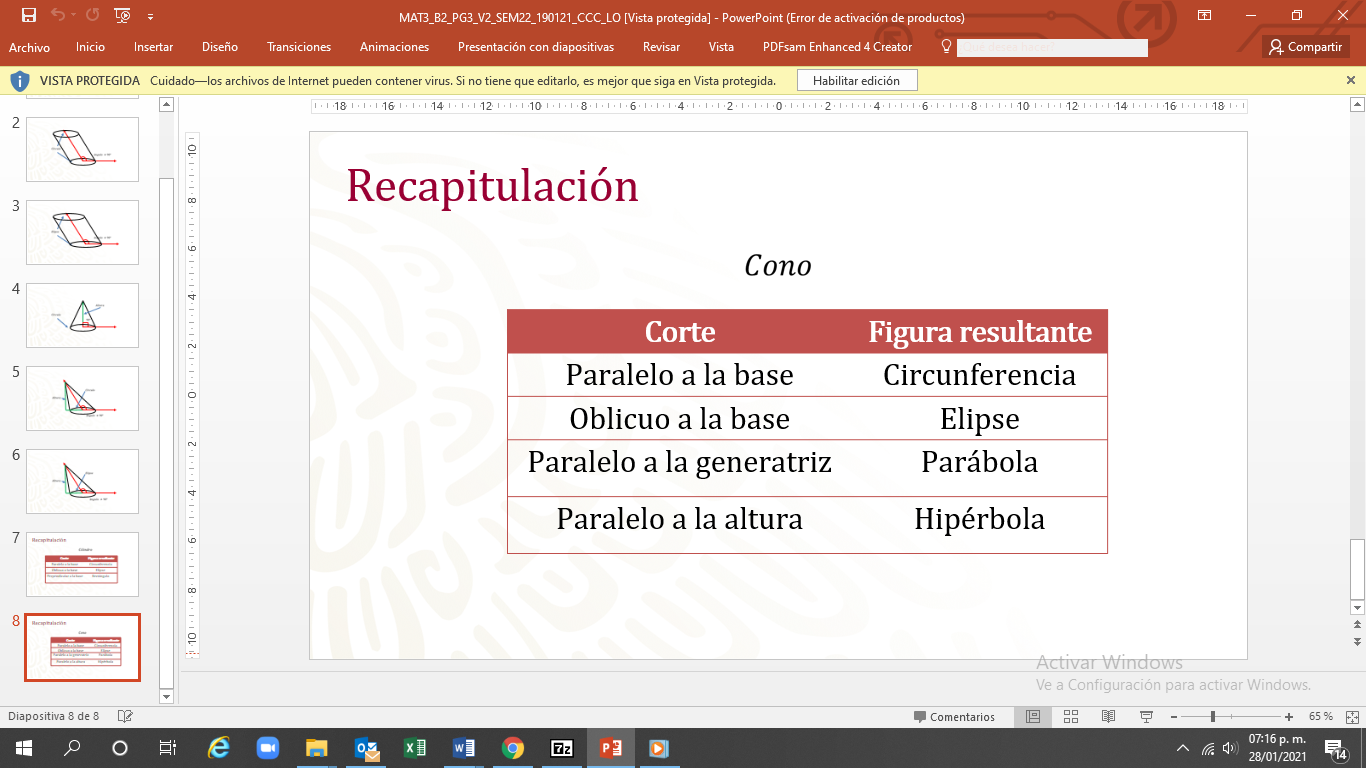
Para el caso del cono se realizaron cuatro cortes.

El primero fue paralelo a la base y obtuvo una circunferencia.

El segundo fue oblicuo a la base, y se obtuvo una elipse, al igual que en el cilindro.

El tercero fue paralelo a la generatriz, y se obtuvo una parábola.

Y el cuarto corte paralelo fue a la altura —y con dos conos unidos por su vértice—, se obtuvo una hipérbola.

El reto de hoy:

Busca en tu libro de texto los diversos usos que se pueden dar a una circunferencia, a una elipse, a una parábola y a una hipérbola.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/secundaria.html