Resolver problemas de cálculo de perímetro y área de polígonos irregulares

Resolver problemas de cálculo de perímetro y área de polígonos irregulares

Aprendizaje esperado: calcula el perímetro y el área de polígonos regulares y del círculo a partir de diferentes datos.

Énfasis: calcular el perímetro y el área de polígonos irregulares.

¿Qué vamos a aprender?

En esta sesión, conocerás cómo calcular el perímetro y el área de polígonos irregulares. Para ello, resolverás diversas situaciones con la finalidad de construir un sentido y un significado sobre el cálculo de estos polígonos.

¿Qué hacemos?

Registra las siguientes preguntas en tu cuaderno para responderlas al finalizar la sesión:

1. ¿Cuál es la importancia de calcular el perímetro y el área de polígonos irregulares?
2. ¿Por qué es necesario dar sentido y significado a estos cálculos?

Inicia a partir de la siguiente consideración.

Un polígono es una figura plana cerrada, formada por tres o más lados rectos. Un polígono puede ser regular (el que tiene todos sus lados y ángulos iguales) o irregular (el que no tiene todos sus lados y ángulos iguales).

Ahora analiza y resuelve el primer problema.

Problema 1

Juan necesita comprar un terreno que mida al menos 4,000 metros cuadrados de superficie, debido a la zona en que quiere adquirirlo, su presupuesto le alcanza para un terreno de esa medida como máximo.

En el periódico encontró a la venta un terreno cuyo croquis se muestra en la siguiente imagen. El croquis sólo muestra las medidas de sus lados pero no indica cuál es su superficie, por lo que Juan quiere averiguarlo.

¿La superficie de este terreno cumple con las características que busca Juan?

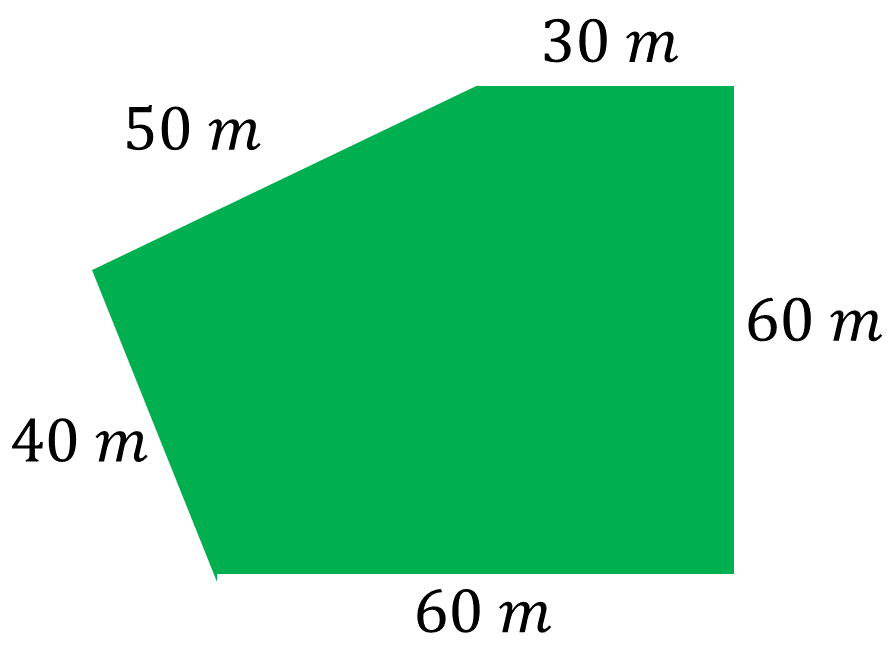
Toma un momento para reflexionar acerca de lo que harías para contestar la pregunta. Anota tus conclusiones en tu cuaderno.

Para verificar tus resultados, analiza lo que hizo Juan. Él identifica la figura como un pentágono irregular, por lo que la fórmula: área igual a perímetro por apotema entre 2, no es posible aplicarla para calcular el área de este polígono, ya que esa fórmula se utiliza para los polígonos regulares y la forma del terreno no cumple con esas características porque la medida de sus lados es distinta, así como la medida de sus ángulos.

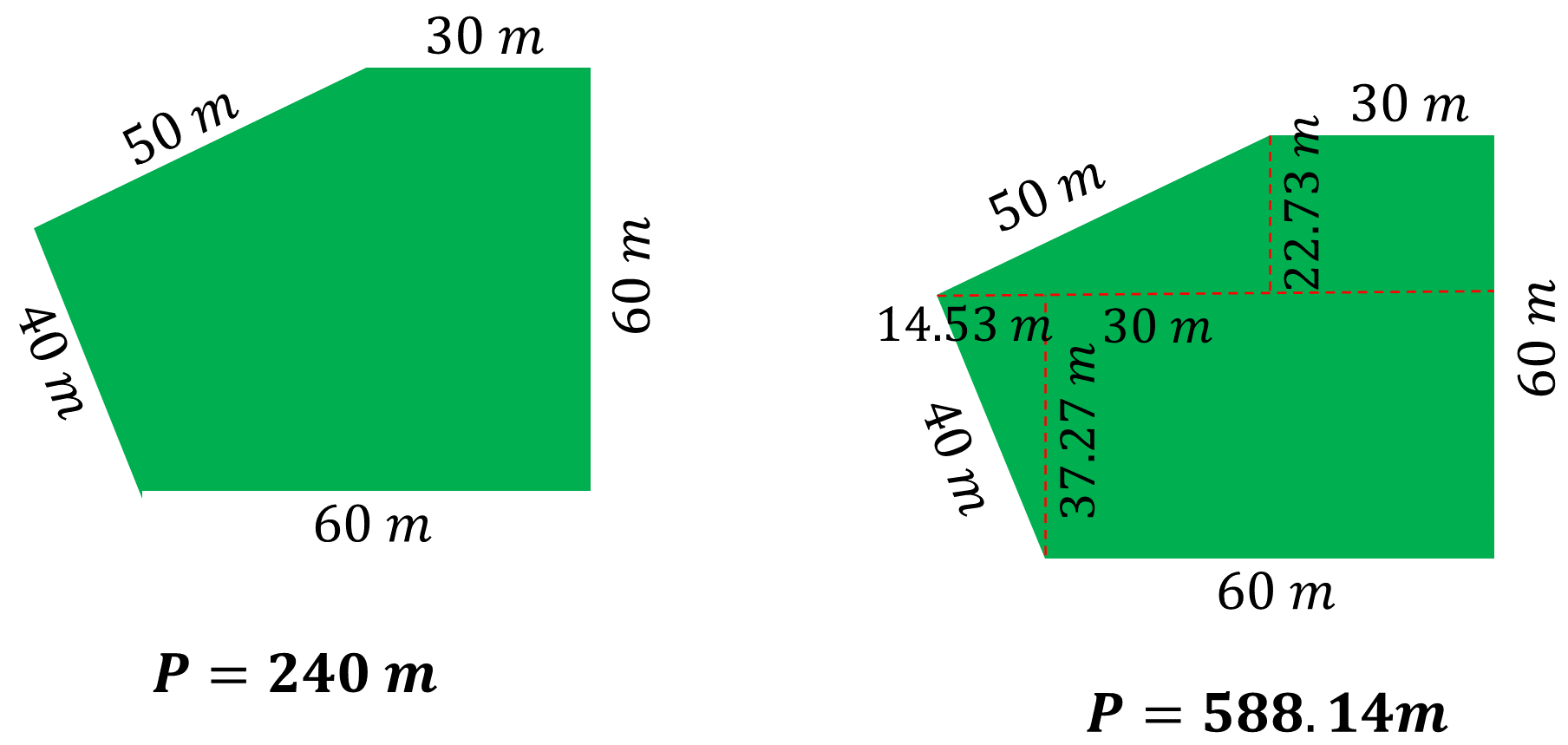
Entonces, Juan midió la imagen del periódico y determinó la escala de la figura, posteriormente, decidió dividir el polígono irregular en figuras cuyas fórmulas para calcular su área ya conocía. Observa la siguiente imagen.

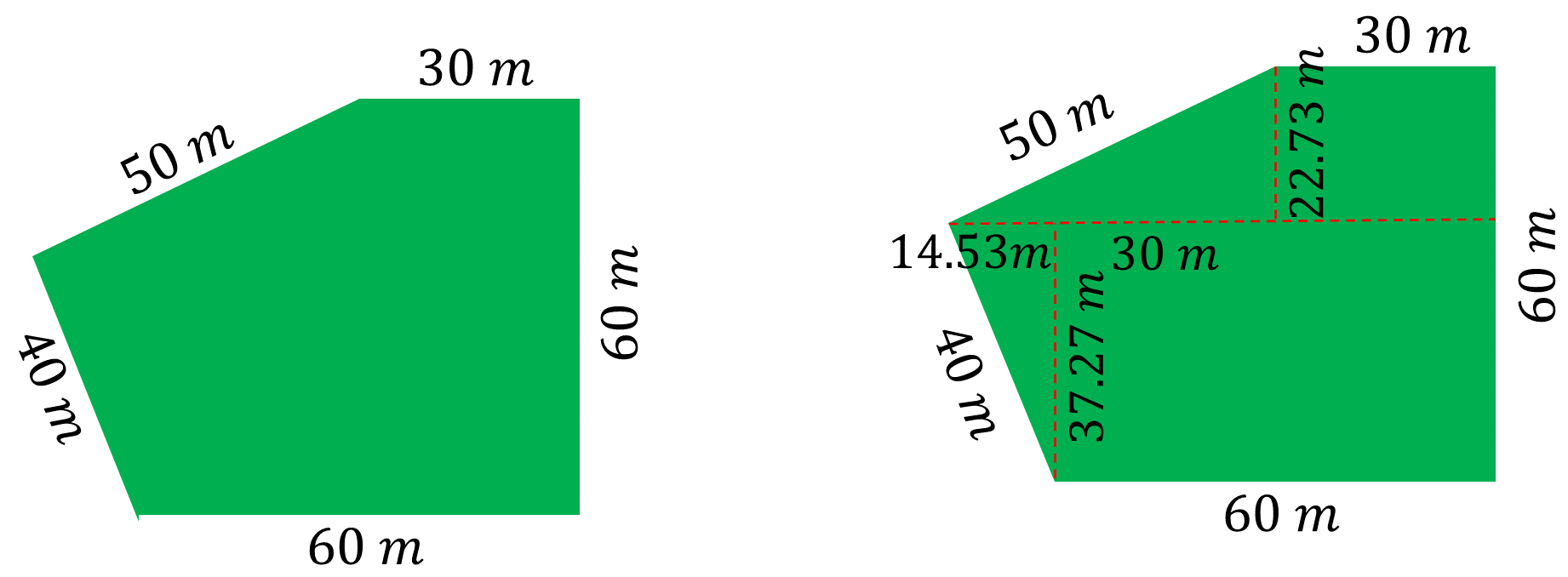
¿En qué figuras dividió Juan el polígono irregular?, ¿se podría hacer la división del polígono de diferente manera?

Con esta división, Juan se da cuenta de que el terreno tiene dos ángulos rectos: uno formado por los lados de 60 metros, otro por el lado de 30 metros y uno de 60 metros. Entonces, él recuerda algunas figuras con ángulos interiores que son rectos. Una de ellas es el rectángulo, por lo que Juan trata de dividir el terreno de manera que pueda tener rectángulos en su interior.

Juan traza varias líneas y toma las medidas de los segmentos que forman las figuras, considerando la escala de la imagen de las cuales ya conoce la manera de calcular el área.

Traza una primera línea horizontal paralela al lado que se observa como la base del polígono, formando dos polígonos irregulares. Después, traza una primera línea vertical perpendicular a la base del polígono y forma un rectángulo de 60 metros de largo y, al medir, obtuvo que el ancho era de 37.27 metros. Con la misma línea determina un triángulo considerando la escala de la imagen del periódico, resultaron lados de 14.53 metros, 37.27 metros y 40 metros.

Posteriormente, traza una segunda línea vertical perpendicular para dividir el sector restante en un rectángulo y en un triángulo. Este rectángulo mide 30 metros de largo y 22.73 metros de ancho. Los lados del triángulo, formado con esta segunda línea, miden 50 metros, 22.73 metros y 44.53 metros.

Por lo tanto, Juan dividió el pentágono irregular en dos rectángulos y dos triángulos, figuras de las cuales ya conoce las fórmulas para calcular su área.

¿Qué debe hacer Juan a continuación? Juan debe calcular el área de los rectángulos y triángulos. Una manera es aplicar la fórmula:

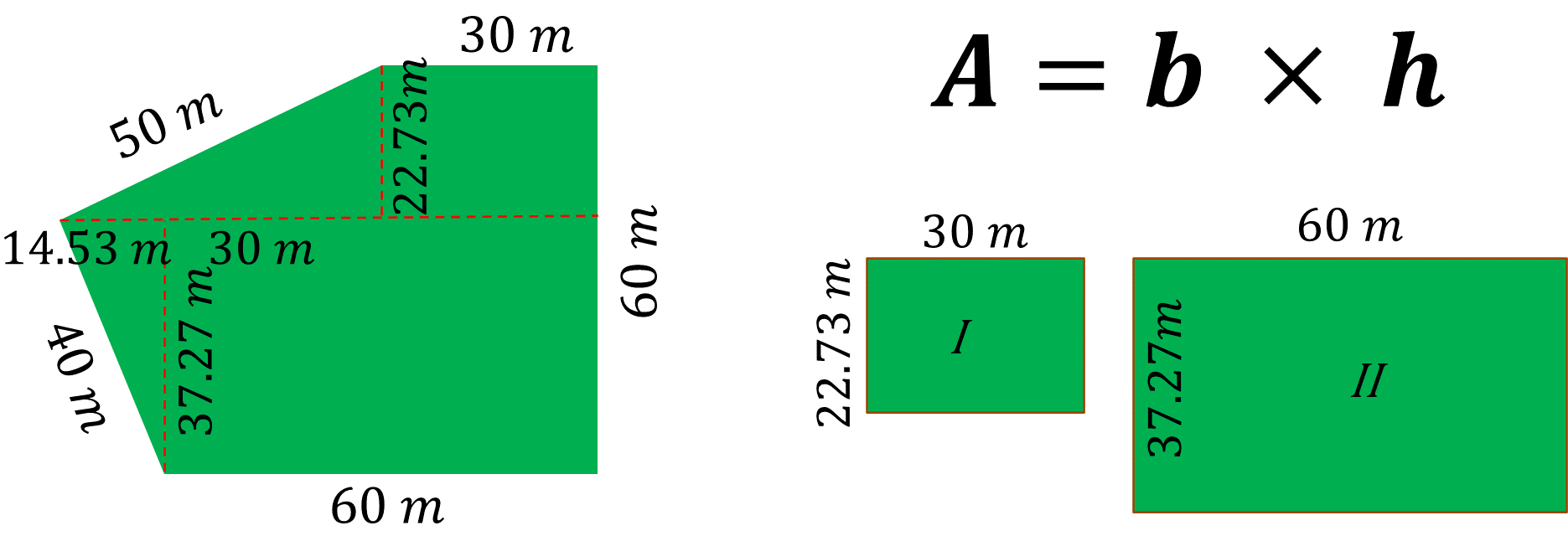
Donde:

A: representa el valor del área.

b: representa la medida de la base.

h: representa la medida de la altura.

Ahora, utilizando la fórmula, calcula el área del rectángulo uno y rectángulo dos.

Para el rectángulo uno, al sustituir valores en la fórmula se tiene lo siguiente:

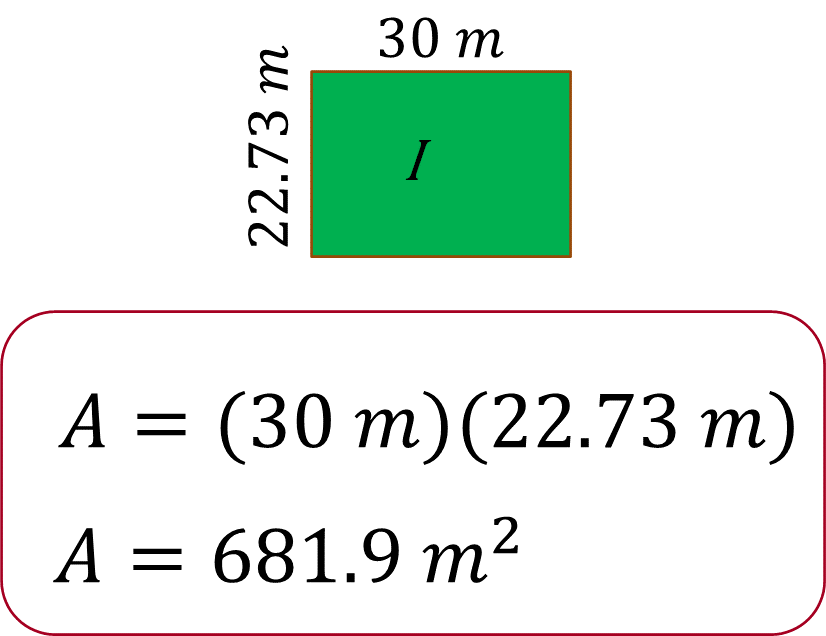
Por lo tanto, se obtienen 681.9 metros cuadrados.

Para el rectángulo dos, la sustitución en la fórmula es:

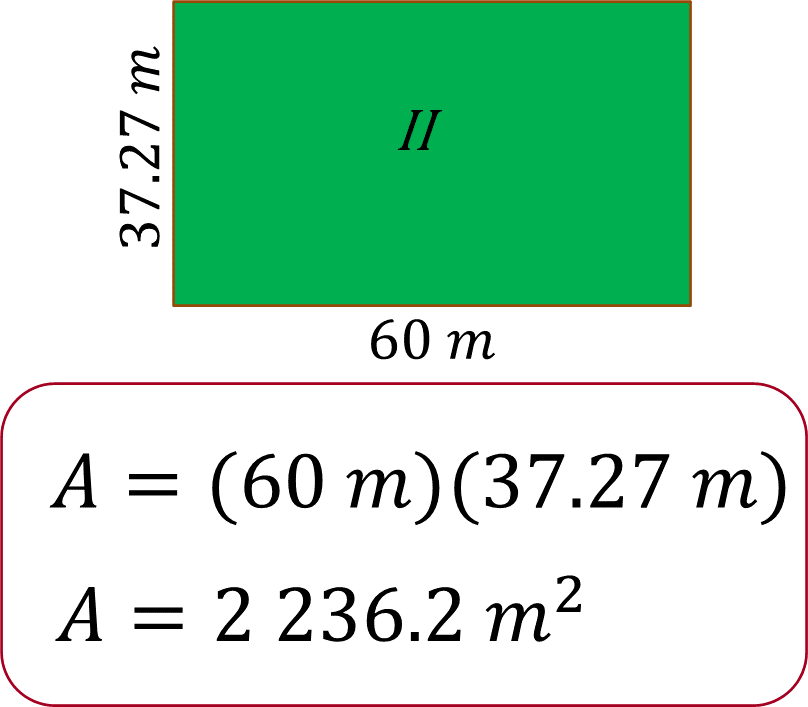
Se obtiene, 2236.2 metros cuadrados.

Ahora, al sumar el valor de las áreas de los dos rectángulos se tienen 681.9 metros cuadrados más 2 236.2 metros cuadrados que es igual a 2918.1 metros cuadrados.

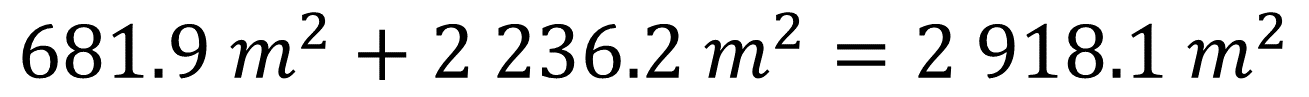
La medida obtenida representa el área que ocupan los rectángulos dentro del terreno que necesita comprar Juan.

Ahora, ¿qué se debe hacer para continuar con la resolución del problema? Se debe calcular el área de los triángulos.

Se sabe que el terreno fue dividido por Juan en 2 rectángulos y 2 triángulos. Para calcular el área de los triángulos, una manera es utilizar la siguiente fórmula:

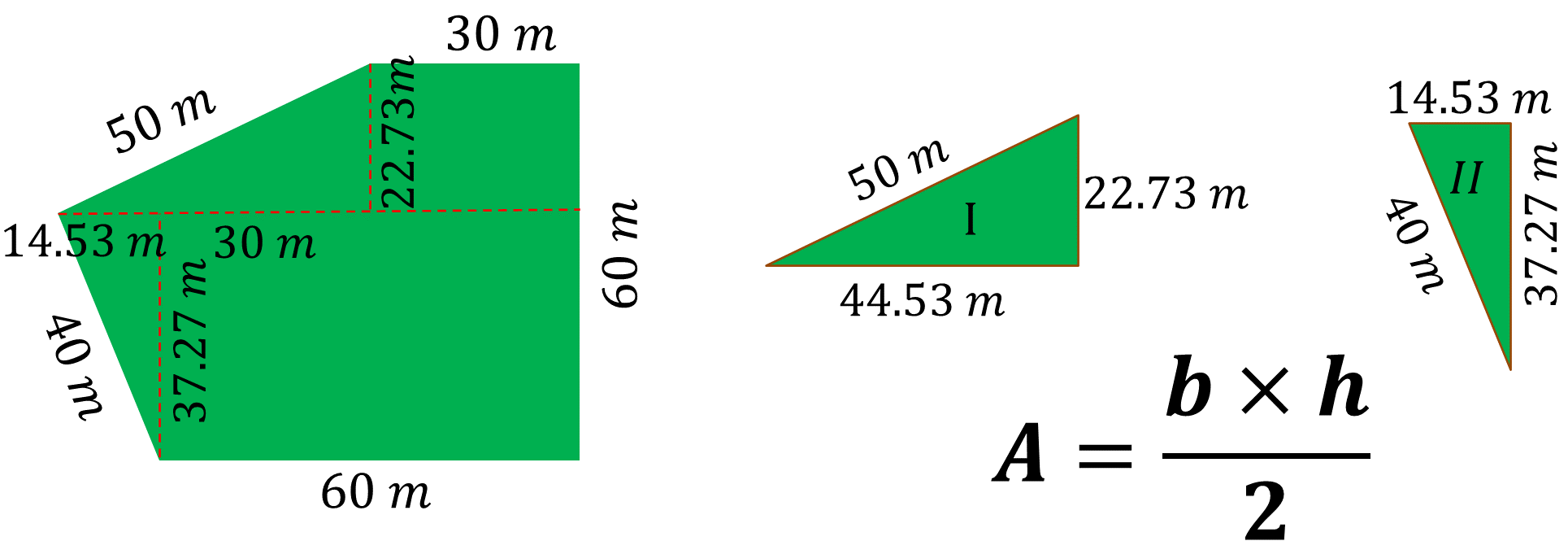
Calcula el área del triángulo uno y del triángulo dos.

Para el área del triángulo uno, al sustituir los valores en la fórmula se tiene que:

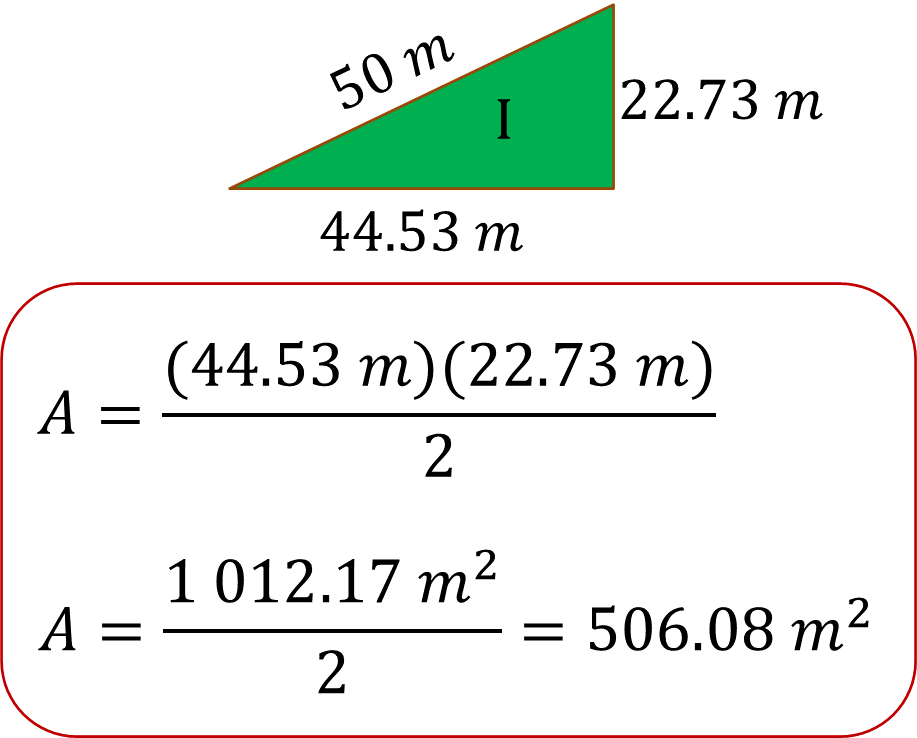
Con lo anterior, se obtienen 506.085 metros cuadrados.

Para el triángulo dos, el área es igual a:

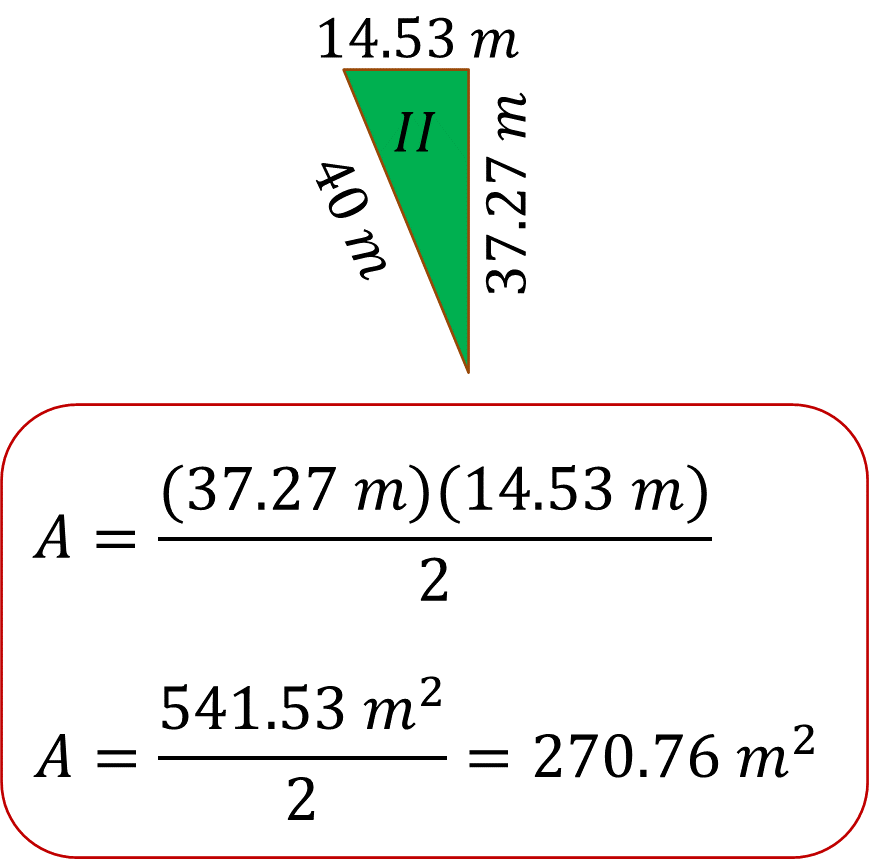
El producto es 270.76 metros cuadrados.

Ahora, suma el valor de las áreas de los dos triángulos: 506.08 metros cuadrados más 270.76 metros cuadrados, que es igual a 776.84 metros cuadrados.

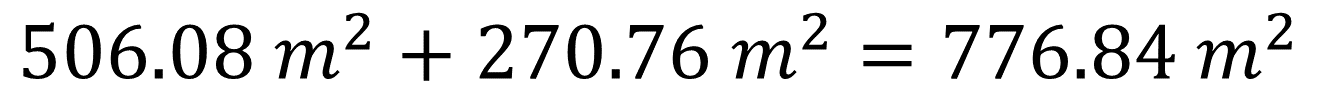
Con el área de los triángulos dentro del terreno que quiere comprar Juan, ya se puede calcular el área total del terreno. Para ello, Juan sumó el área total de los rectángulos más el área total de los triángulos, es decir, 2918.1 metros cuadrados más 776.84 metros cuadrados que es igual a 3694.94 metros cuadrados.

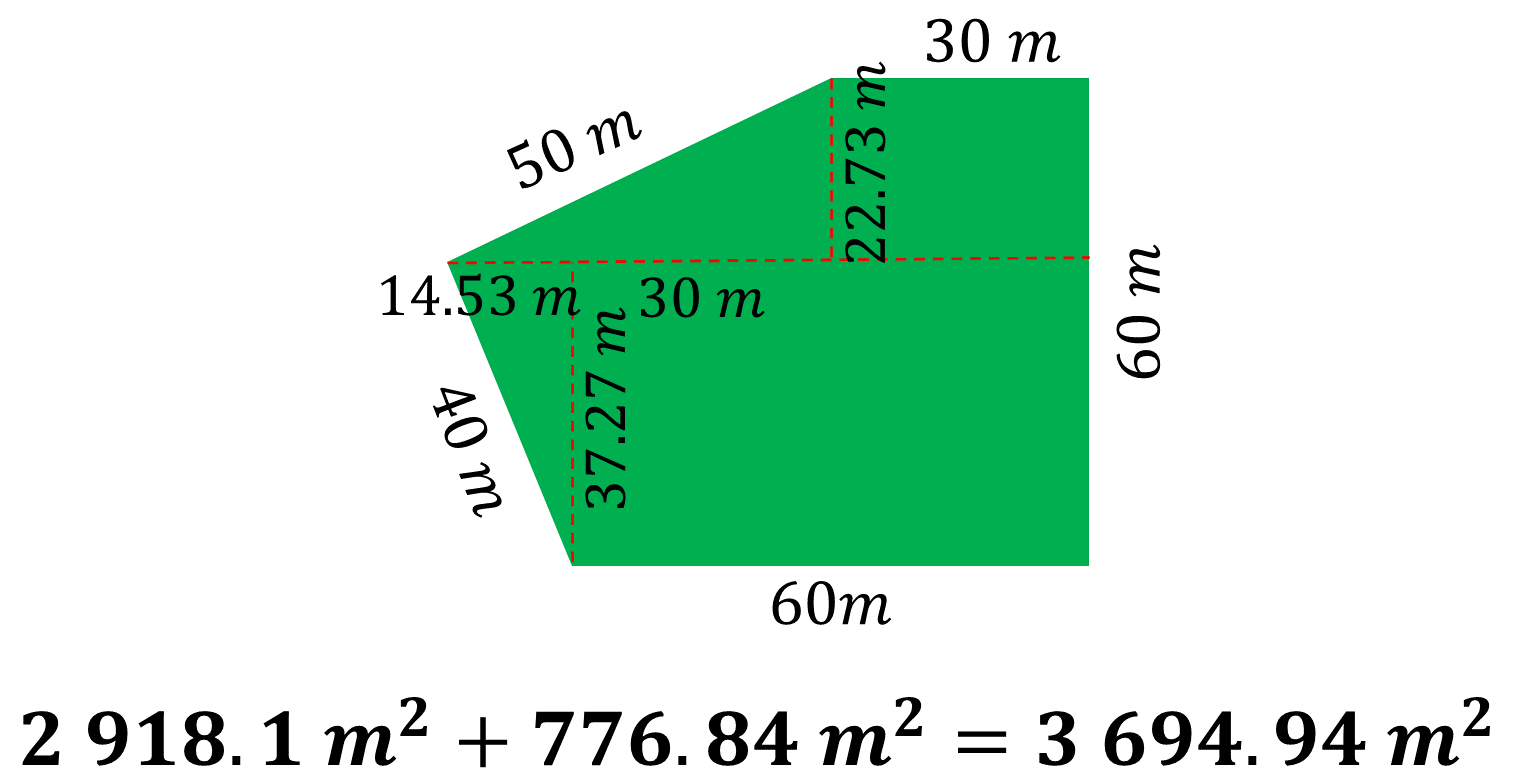
El propósito del problema es determinar si el terreno cumple con la condición de tener como máximo 4000 metros cuadrados para que Juan se interese en comprarlo. ¿Este terreno cumple con esa condición? Sí cumple porque su área es menor a la máxima requerida por Juan, que son 4000 metros cuadrados.

Ahora, reflexiona en lo siguiente: ¿cómo se calculó el área del terreno?

Se dividió el terreno en superficies parciales, en este caso, en rectángulos y triángulos. Luego, se calcularon sus áreas, por lo tanto, el área total es igual a la suma de las áreas parciales.

Ahora, resuelve la siguiente situación de este mismo problema.

En caso de realizar la compra, Juan piensa cercar el terreno poniendo tres hilos de alambre en cada lado. Si decide comprarlo, ¿qué cantidad de alambre requiere?

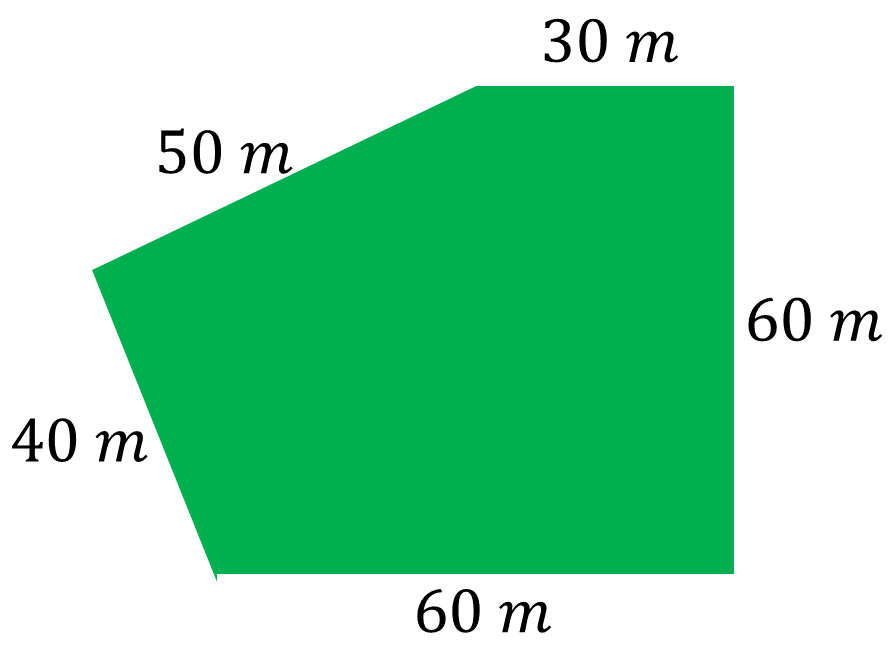
Calcula la cantidad de alambre que Juan necesitaría para cercar el terreno. Realiza tus cálculos y contesta la siguiente pregunta: ¿qué medidas del polígono irregular calculaste?

Para dar respuesta a la pregunta, se debe calcular el perímetro de este polígono. Una manera de calcular el perímetro de un polígono regular es multiplicar la medida de un lado por el número de lados. ¿Es posible aplicar esta fórmula en este polígono?

En este caso no es posible aplicar esa fórmula, porque esa fórmula se aplica en los polígonos regulares porque todos sus lados tienen la misma medida, pero en este caso, los lados del polígono no son todos de la misma medida, así que se debe usar otra forma de calcular su perímetro.

Una manera de calcular el perímetro del terreno, que tiene forma de un polígono irregular, es sumar las medidas de sus lados. Por lo tanto, el valor del perímetro es igual a:

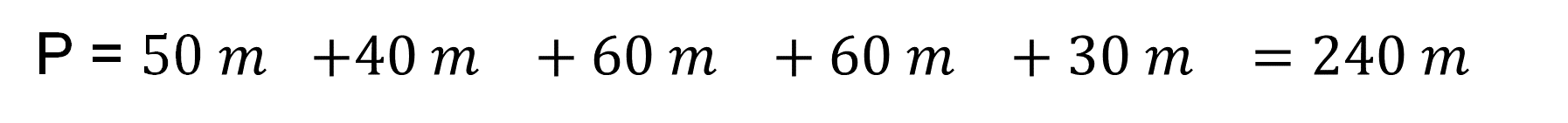
Ahora, ¿qué se tiene que hacer con la medida del perímetro para calcular la cantidad de alambre necesario para cercar el terreno? Se debe multiplicar por 3, porque el problema dice que Juan quiere colocar tres hilos de alambre en cada lado. Entonces, se multiplica 3 por 240 metros, lo que resulta 720 metros, siendo ésta la cantidad necesaria para colocar 3 hilos de alambre alrededor del terreno.

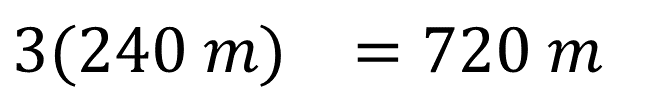
En la primera parte de este problema se llegó a la conclusión de que el área del polígono irregular es igual a la suma de las áreas de las figuras en que se puede dividir, pero ¿pasará lo mismo con el perímetro

Anteriormente, se calculó el perímetro del polígono y se obtuvo 240 metros. Ahora, da respuesta a la siguiente pregunta: ¿cuál es la suma de los perímetros de los triángulos y de los rectángulos en que se dividió el polígono?

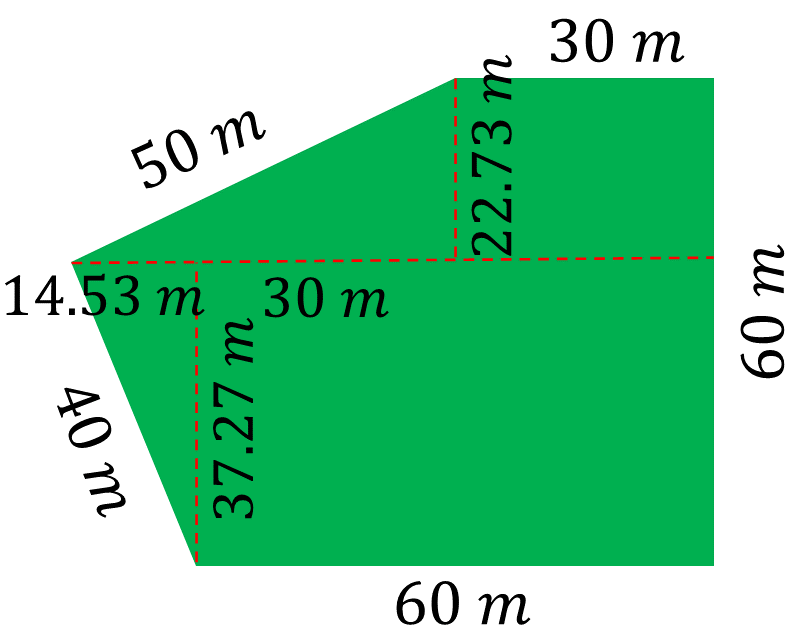
Para ello, calcula los perímetros de los triángulos y de los rectángulos. Así como la suma de estos perímetros.

Para calcular el perímetro de los triángulos, suma las medidas de sus lados. Para el caso de un triángulo se tiene que su perímetro es igual a 50 metros más 44.53 metros, más 22.73 metros, con lo que se obtiene que el perímetro es 117.26 metros.

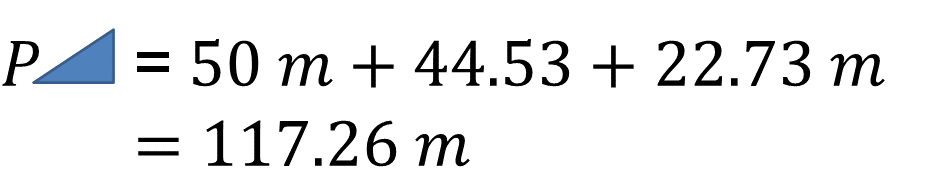
En el caso del otro triángulo, se suman 40 metros, más 37.27 metros, más 14.53 metros, por lo que el perímetro de este triángulo es de 91.8 metros.

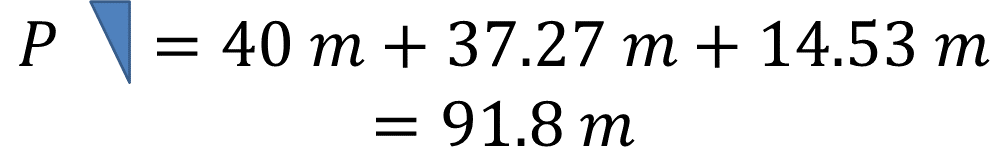
Para el caso de un rectángulo, multiplica 2 por 60 metros y a este producto se le suma el resultado de multiplicar 2 por 37.27 metros. Al resolver las operaciones se obtienen 194.54 metros, correspondiente al valor del perímetro de este rectángulo.

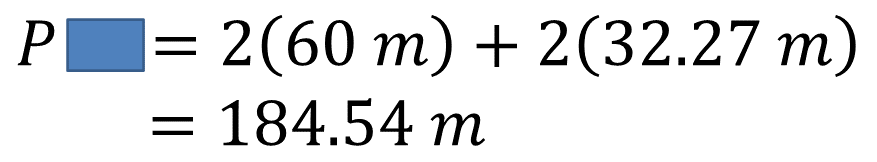
Para el otro rectángulo, se multiplica el valor de la base por 2, el valor de la altura por 2 y se suman los productos de dichas multiplicaciones. Es decir, 2 por 30 metros más 2 por 22.73 metros. De esta manera, se determina que el perímetro de este rectángulo es de 105.46 metros.

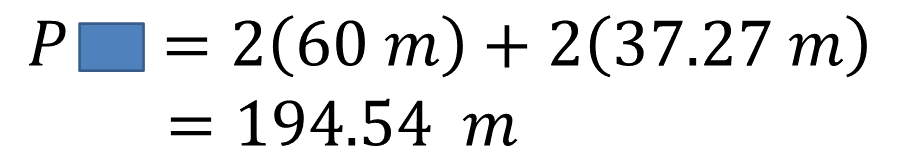
Finalmente, la suma de los perímetros de las figuras anteriores: 117.26 metros, más 91.8 metros, más 194.54 metros, más 194.54 metros. De esta forma, se obtienen 588.14 metros.

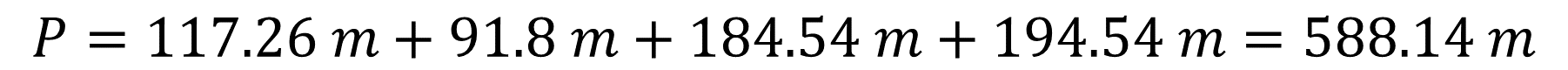
¿Este resultado es igual al perímetro del polígono irregular? El perímetro que se obtuvo anteriormente para el polígono irregular fue de 240 metros y la suma de los perímetros de las figuras en que se dividió ese polígono es de 509.6 metros. En este caso, el perímetro de las figuras en que se dividió el polígono no es igual al perímetro de ese polígono.

No olvides registrar tus dudas o inquietudes en tu cuaderno para luego comentarlas con tus compañeras, compañeros y con tus docentes para aclararlas, esto en la medida de lo posible.

A continuación, analiza lo siguiente. Observa la siguiente figura ABCDE. ¿Cómo se calcula el área de este polígono irregular?

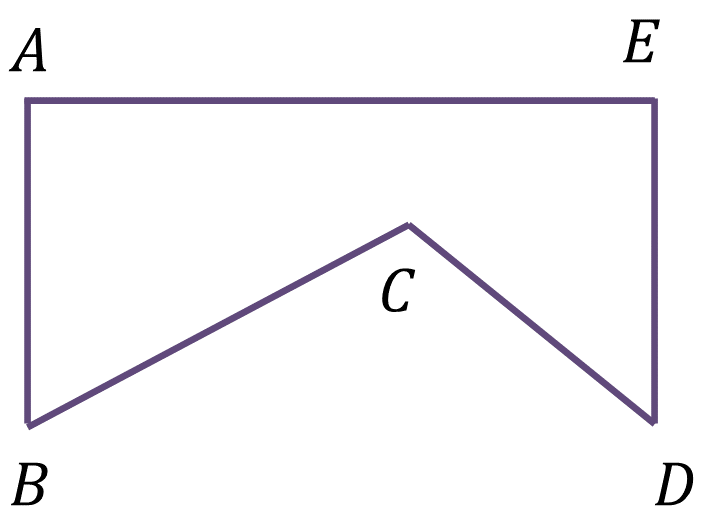
Reflexiona: Si se divide en otras figuras, de las cuales ya conoces una manera de calcular su área, ¿cuántas figuras se pueden obtener al dividir esta figura?, ¿cuántas líneas se pueden trazar para hacer la división de la figura?

Observa la siguiente imagen.

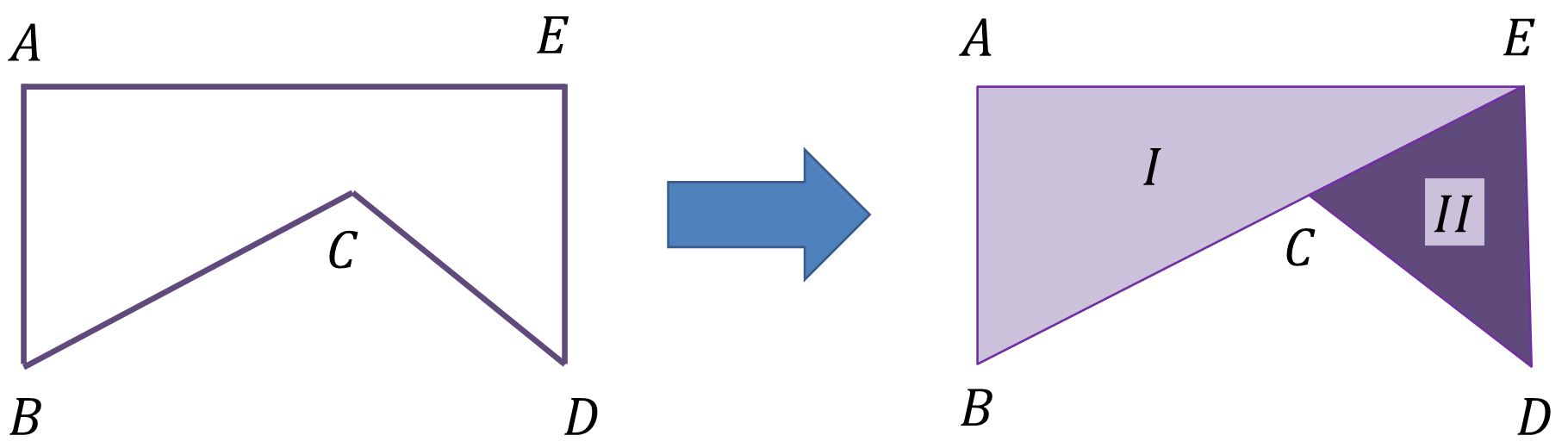
En esta manera de dividir el polígono irregular, se prolongó el lado BC hasta el vértice E. Así, el polígono irregular se dividió en dos triángulos. Pero ¿será la única manera en que se puede dividir el pentágono irregular?, ¿de qué otra forma se te ocurre?

Observa otra imagen al respecto.

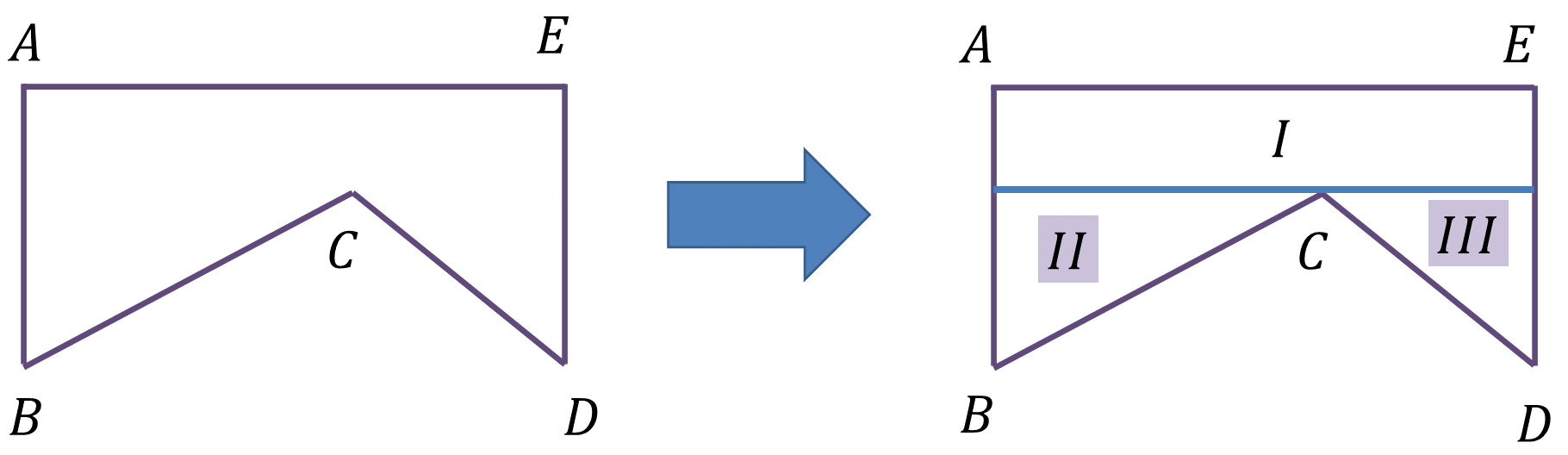
En esta otra forma que se presenta, se puede observar que se trazó una línea al interior del polígono. Esa línea pasa por el vértice C, es paralela al segmento AE y perpendicular a los segmentos AB y ED. Así, divide al polígono en tres figuras, que según las medidas de los ángulos son un rectángulo y dos triángulos.

Ahora, continúa con otra manera de calcular el área de un polígono irregular. Presta mucha atención y realiza las actividades que se pidan.

Las siguientes figuras son dos trapezoides, son cuadriláteros y no tienen lados paralelos. Obsérvalas. ¿Qué figura se forma al trazar los segmentos de recta rojos?

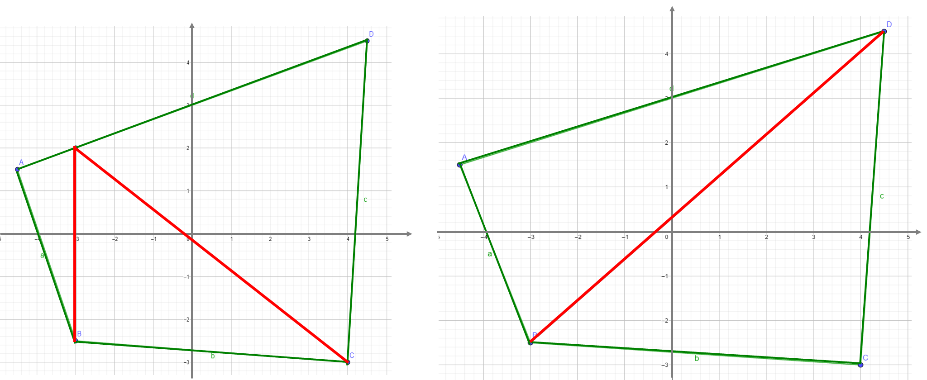
Se forman triángulos. Inténtalo, traza polígonos irregulares y divídelos de manera tal que, puedas dividirlos en triángulos para poder calcular su área. Observa otros ejemplos.

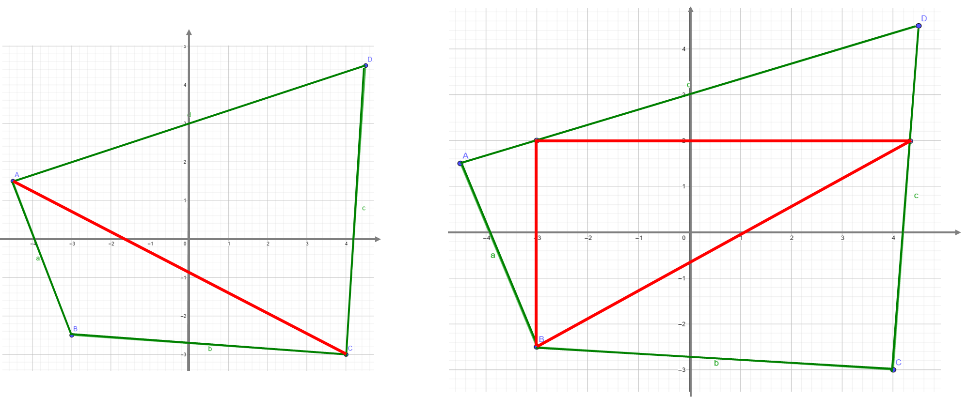
Si tienes la ventaja de contar con un papel cuadriculado sobre el cual esté trazado el polígono, puedes emplear la cuadrícula para contar la cantidad de cuadrados completos que hay dentro del polígono y con los cuadrados que no se completaron, agrupar las partes que los forman y hacer una aproximación a un cuadrado completo, para posteriormente adicionarlos. Analiza y realiza una aproximación del área total de la figura.

De los polígonos irregulares, trabajarás con el que se muestra a continuación. Porque al ser dividida en otras figuras, es la que menor cantidad de ellas tiene.

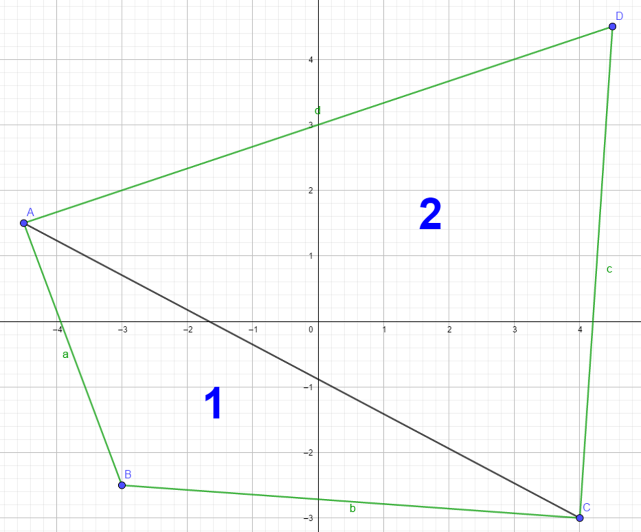
Al trazar la diagonal del trapezoide que se muestra, éste quedó dividido en dos triángulos. El “triángulo 1”, que se formó en la parte inferior y el “triángulo 2” que está en la parte superior. ¿Cuál es la fórmula para calcular el área de esas figuras?, ¿cuentas con los datos necesarios para calcular su área? Es importante que anotes las operaciones y trates de resolverlas.

Para calcular el área, se necesitan conocer las alturas de los triángulos. Para ello, puedes trazar líneas auxiliares, perpendiculares a alguna de sus bases.

Gira la figura para que observes las bases como comúnmente se muestran, en posición horizontal, pero es importante reconocer mentalmente e identificar cualquiera de las bases, independientemente de la posición de la figura.

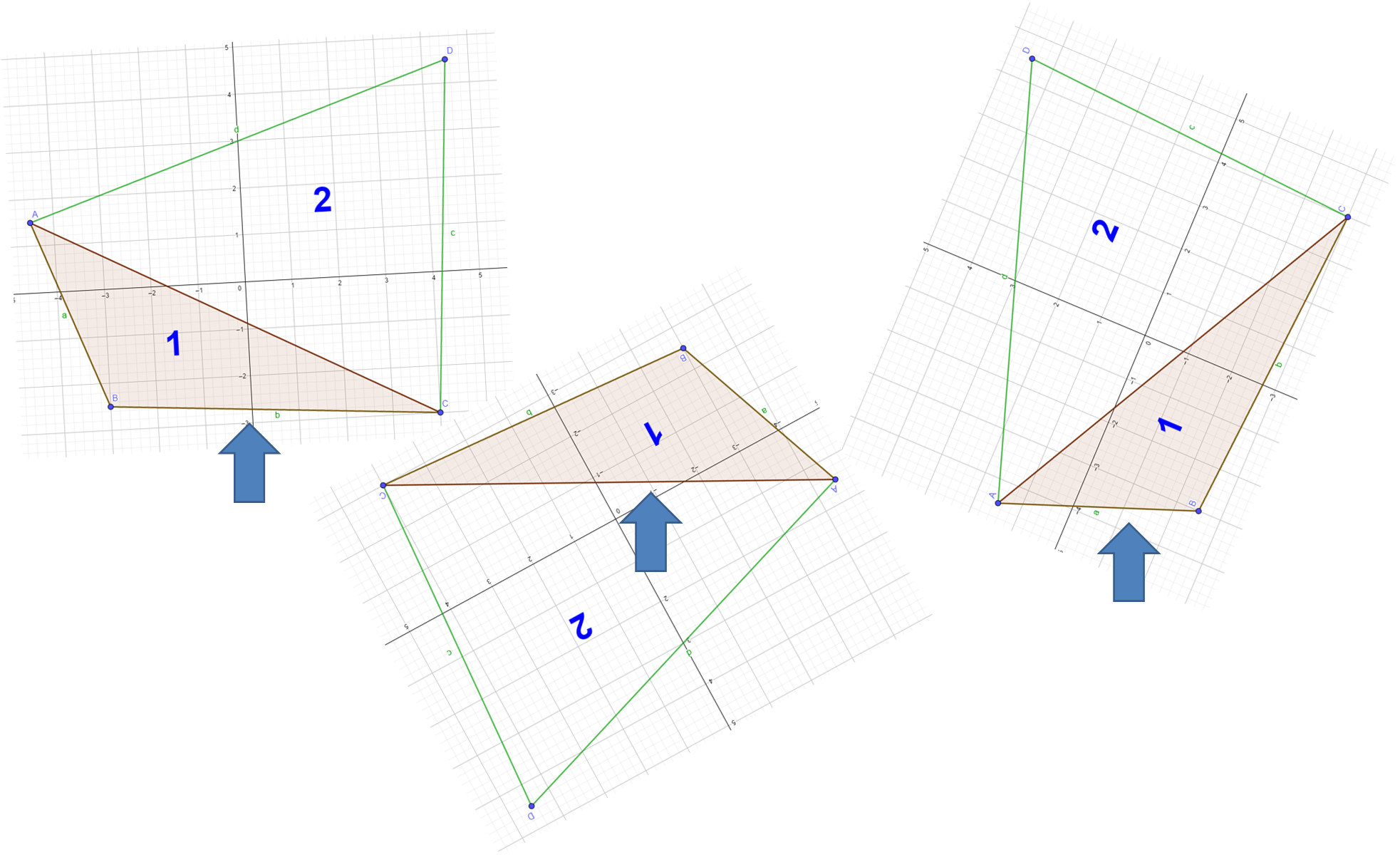
Una vez que hayas reconocido la base, identifica las alturas, el triángulo tiene 3 alturas.

En el caso del triángulo 1, no todas sus alturas están dentro de él, por lo tanto, prolonga algunos de sus lados para poder encontrar el segmento perpendicular a la base y que toca el vértice más alto.

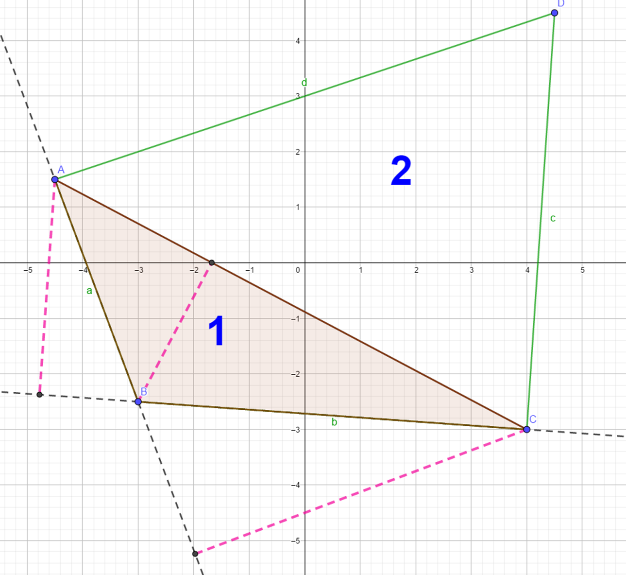
Ahora, reflexiona: ¿con cuál de las 3 alturas trabajarías? En esta ocasión, trabajarás con la altura que está dentro del triángulo, y tomarás las medidas de su base y de la altura.

La base AC mide 9.62 unidades y su altura FB mide 2.83 unidades, como se muestra en la imagen.

Calcula el área del triángulo con la fórmula base por altura sobre dos y sustituye los valores, obteniendo lo siguiente:

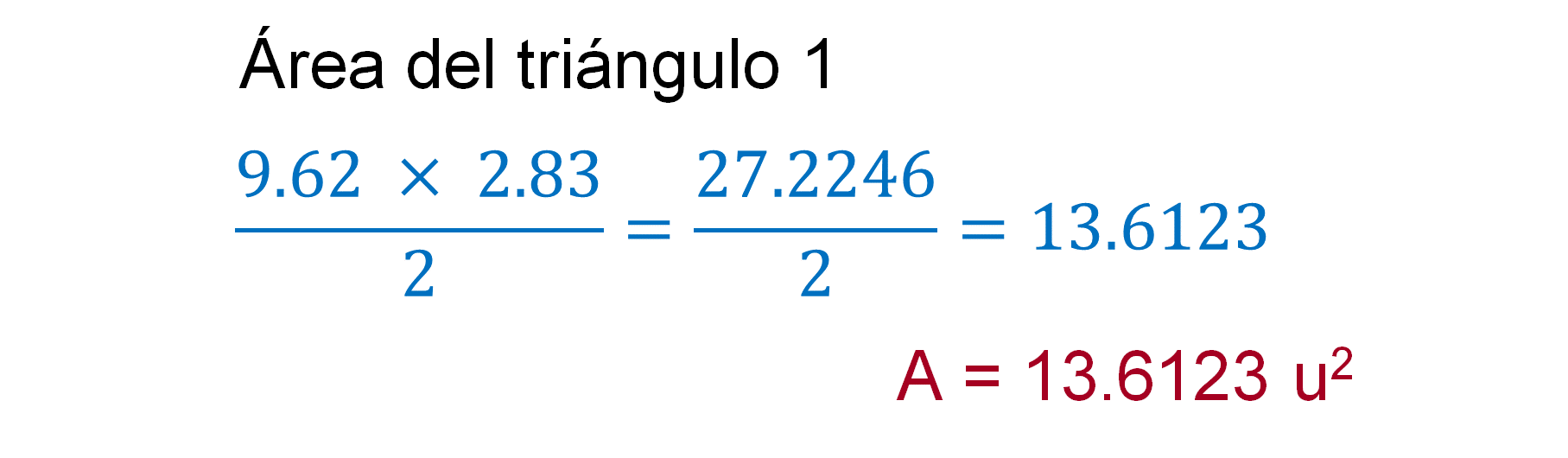
Al sustituir los datos en la fórmula, el resultado es 13.6123. Este resultado es el área, por lo tanto, son unidades cuadradas.

De igual manera, elige una base del segundo triángulo y tomando como referencia esa base, mide su altura. La altura mide 6.86 unidades.

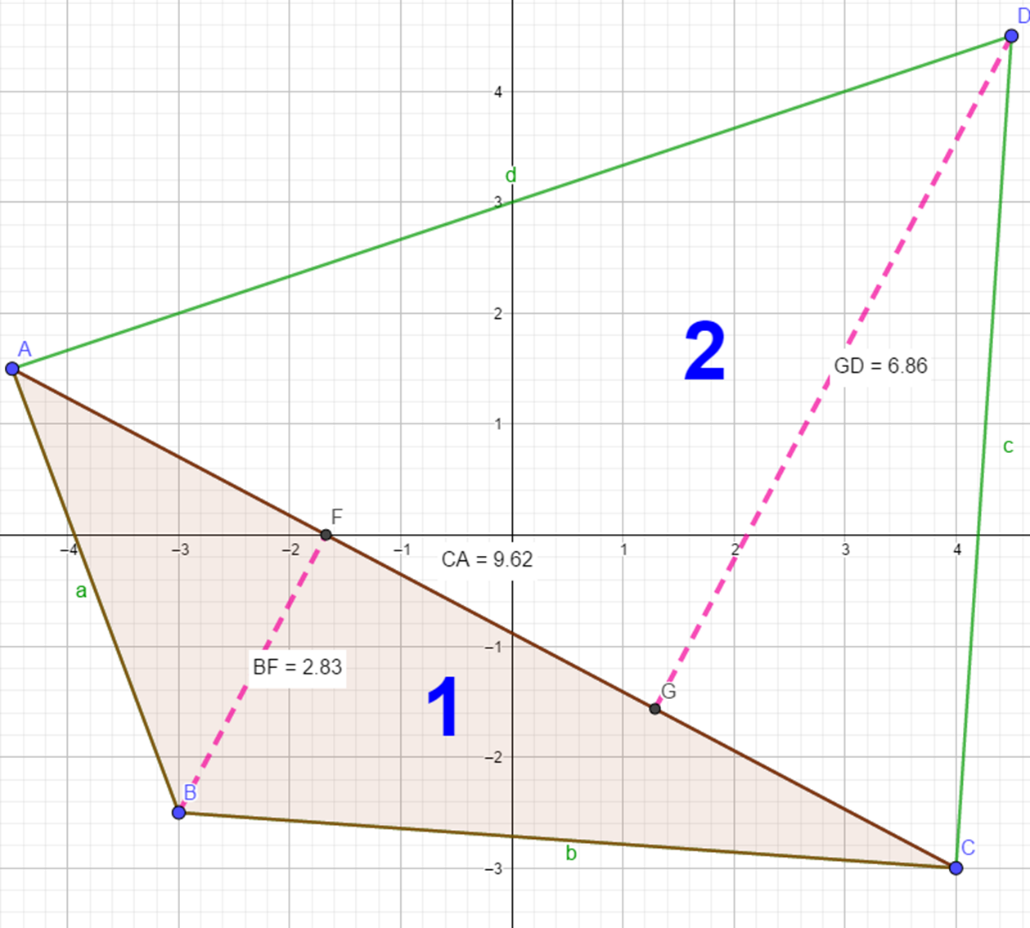
Ahora calcula el área del triángulo 2:

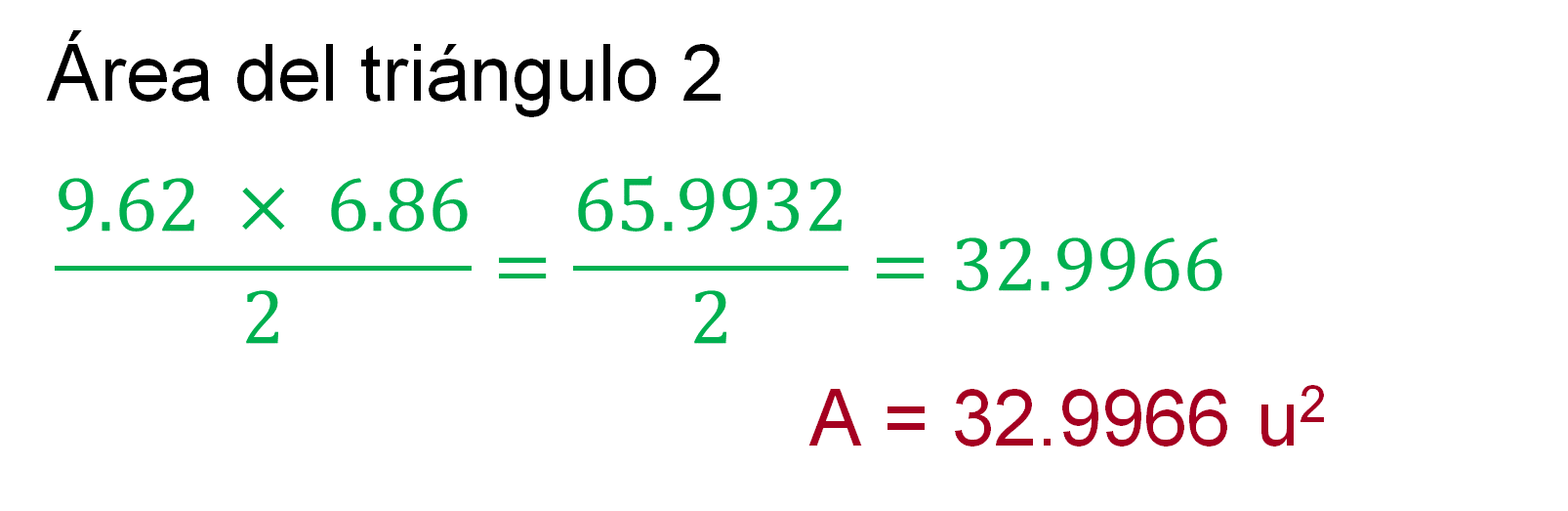
Por lo tanto, el área del triángulo dos es de 32.9966 unidades cuadradas.

Con la información que hasta ahora tienes, ¿qué se debe hacer para encontrar el área total del polígono? Debes sumar el área del triángulo 1 más el área del triángulo 2. En este caso es:

13.6123 + 32.9966 = 46.6089

Con esto has llegado a la solución del problema. ¿De qué otra manera se puede calcular el área del polígono?

Toma un momento para pensar de qué manera podrías contestar la pregunta anterior. Anota tus ideas acerca de esto en tu cuaderno.

Con la actividad anterior has finalizado esta sesión, en la que estudiaste el tema “Resolver problemas de cálculo de perímetro y área de polígonos irregulares”.

El Reto de Hoy:

Reflexiona y responde las siguientes preguntas:

• ¿Cuántas maneras de calcular la medida de la superficie, es decir, el área de un polígono irregular se trabajaron en esta sesión?
• ¿Cuáles fueron esas formas?
• ¿De qué manera se calculó el perímetro del polígono irregular que representó el terreno que quería comprar Juan en la actividad inicial?

Finalmente, resuelve algunos de los problemas o ejercicios sobre el perímetro y área de polígonos irregulares, de tu libro de texto de Matemáticas de segundo grado.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/