Resolución de problemas integradores. Forma, espacio y medida II

Resolución de problemas integradores. Forma, espacio y medida II

Aprendizaje esperado: desarrollar habilidades que le permitan plantear y resolver problemas usando las herramientas matemáticas, tomar decisiones y enfrentar situaciones no rutinarias.

Énfasis: resolver problemas integradores. Forma, espacio y medida.

¿Qué vamos a aprender?

Los materiales que utilizarás en esta sesión son tu cuaderno de apuntes, bolígrafo, lápiz, goma y hojas de colores, regla o escuadra.

En la sesión anterior se analizaron ejercicios sobre rectas y ángulos, figuras planas, teorema de Pitágoras y razones trigonométricas.

Que corresponden al eje de Forma espacio y medida, en esta sesión analizarás ejercicios sobre el mismo eje, pero se abordarán diferentes temas.

Con el mismo formato, es decir, ejercicios sencillos y directos con 4 posibles respuestas y sólo una correcta.

Es importante considerar los 5 pasos para resolver problemas analizado en la sesión anterior.

También considera tomar nota de los ejercicios y estrategias de solución, para posterior consulta y estudio.

¿Qué hacemos?

Observa con cuidado la figura del siguiente ejercicio.

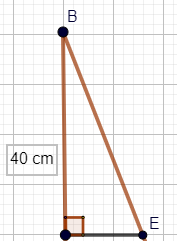
El segmento “DE” es paralelo al segmento “AC” y los ángulos “BCA” y “BDE” son rectos, además el segmento “AC” mide 20 cm y el segmento “BC” mide 50 cm y el segmento “CD” mide 10 cm. ¿Cuál es la medida del segmento “DE”?

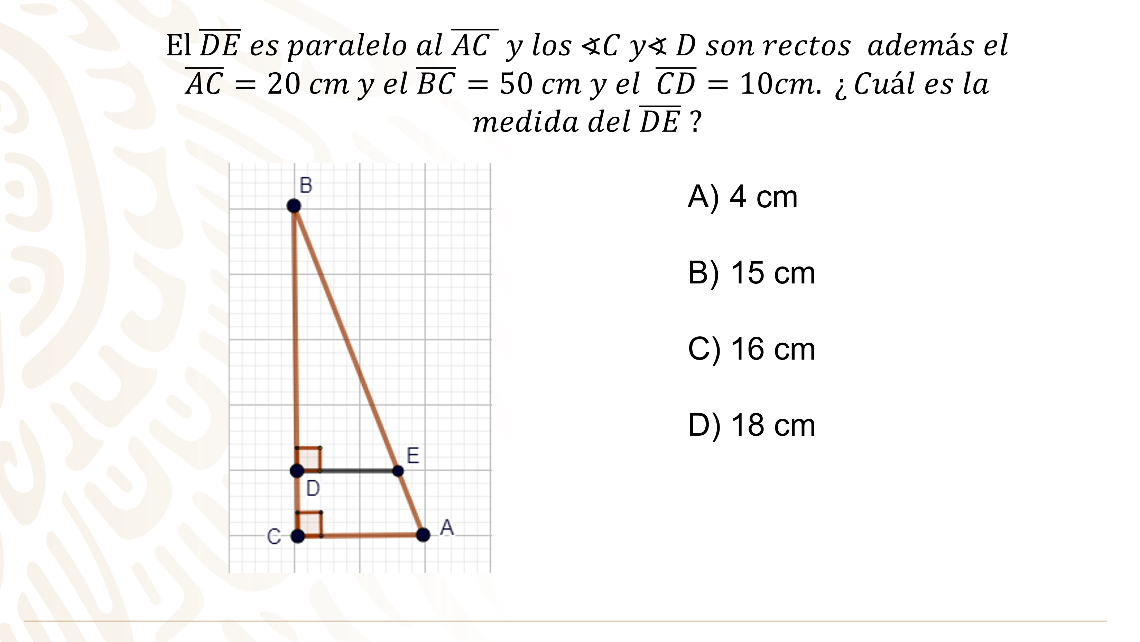
En este tipo de ejercicios es recomendable primero entender a la figura, es decir,

¿Qué representa?

¿Qué papel juegan sus elementos?

Identificar y ubicar los diferentes segmentos que menciona el ejercicio y el que se solicita para su solución,

Para entonces elaborar la estrategia de solución.

Al observar la figura se nota un triángulo rectángulo “ABC” donde su base es paralela con la base del triángulo “BDE”.

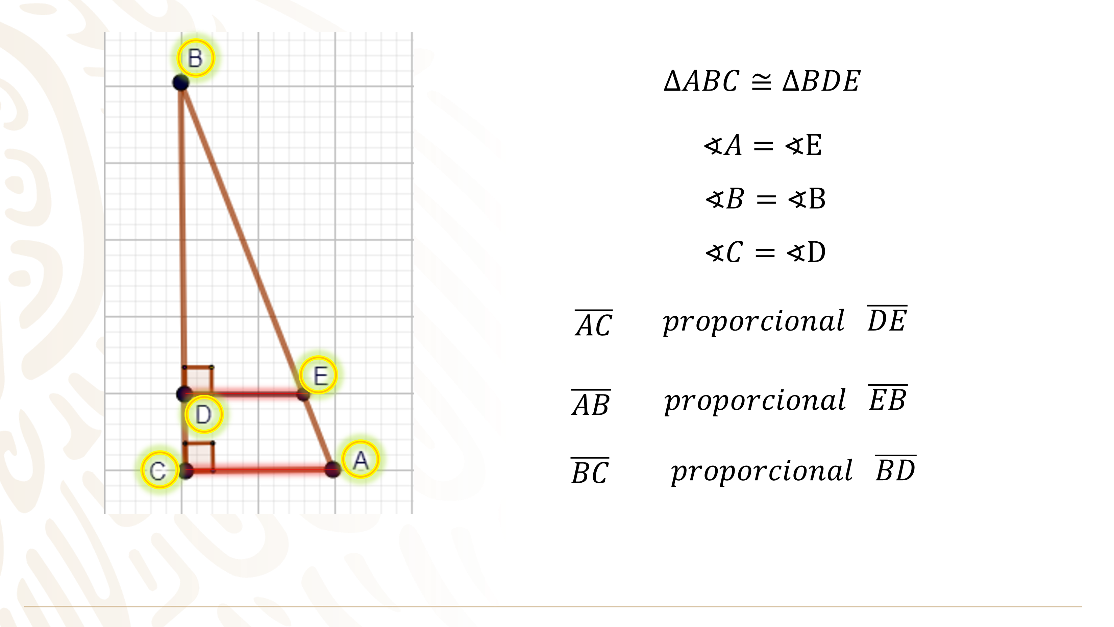
Lo que permite concluir que los triángulos son semejantes ya que tienen la misma forma, ángulos iguales y diferente tamaño, por lo tanto, sus lados homólogos son proporcionales.

Antes de utilizar la representación proporcional entre sus lados, ubica de forma correcta los datos que proporcionan de sus lados.

Proporcionan el segmento “AC” mide 20 cm, el segmento “BC” mide 50 cm y “CD” mide 10 cm.

Y solicitan el segmento “DE”, que lo vas a identificar con la letra “x”.

Cada segmento se escribe sobre su homologo y tienes que:

El segmento “DE” sobre su homologo el segmento “AC”, es igual a el segmento “BD” entre su homologo el segmento “BC”.

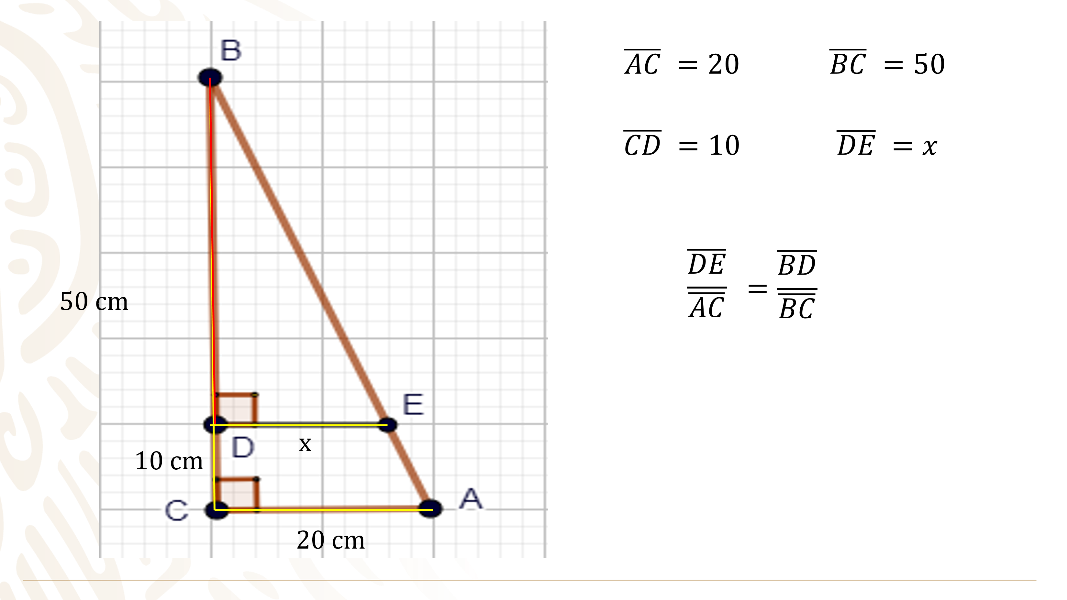
Si observas se desconoce el valor de dos segmentos el segmento “BD” y el segmento “DE” pero uno de ellos es rápido de calcular.

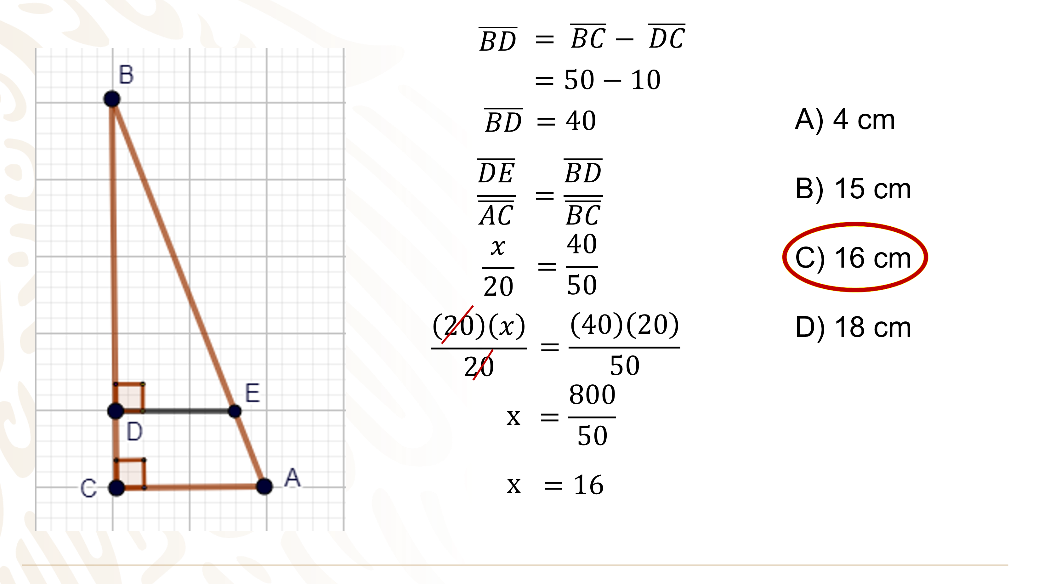
El segmento “BD” por diferencia lo puedes calcular, es igual al segmento “BC” menos el segmento “DC”, sustituyes valores y tienes que es igual a 50 cm menos 10 cm igual a 40 cm.

Ahora sustituye en la igualdad de proporciones y tienes que:

“x” sobre 20 es igual a 40 sobre 50, para despejar a “x” multiplicas a ambos miembros de la igualdad por 20, realizas operaciones y tienes que “x” es igual a 800 entre 50, igual 16 cm.

La respuesta correcta es el inciso C.

Por tratarse de un ejercicio con triángulos rectángulos, puedes pensar que la estrategia de solución puede ser por teorema de Pitágoras.

Pero ¿por qué no es posible?

Aunque el ejercicio involucre triángulos rectángulos no siempre es posible resolver por Teorema de Pitágoras porque para ello se deben conocer dos lados del triángulo para calcular el tercero y del triángulo “BDE” solo se conoce el valor del segmento “BD” por lo tanto, con dos lados desconocidos no es posible aplicar el teorema de Pitágoras sin embargo el teorema de Tales si facilita el cálculo.

Para que quede más claro la utilidad y versatilidad del teorema, analiza el siguiente ejercicio:

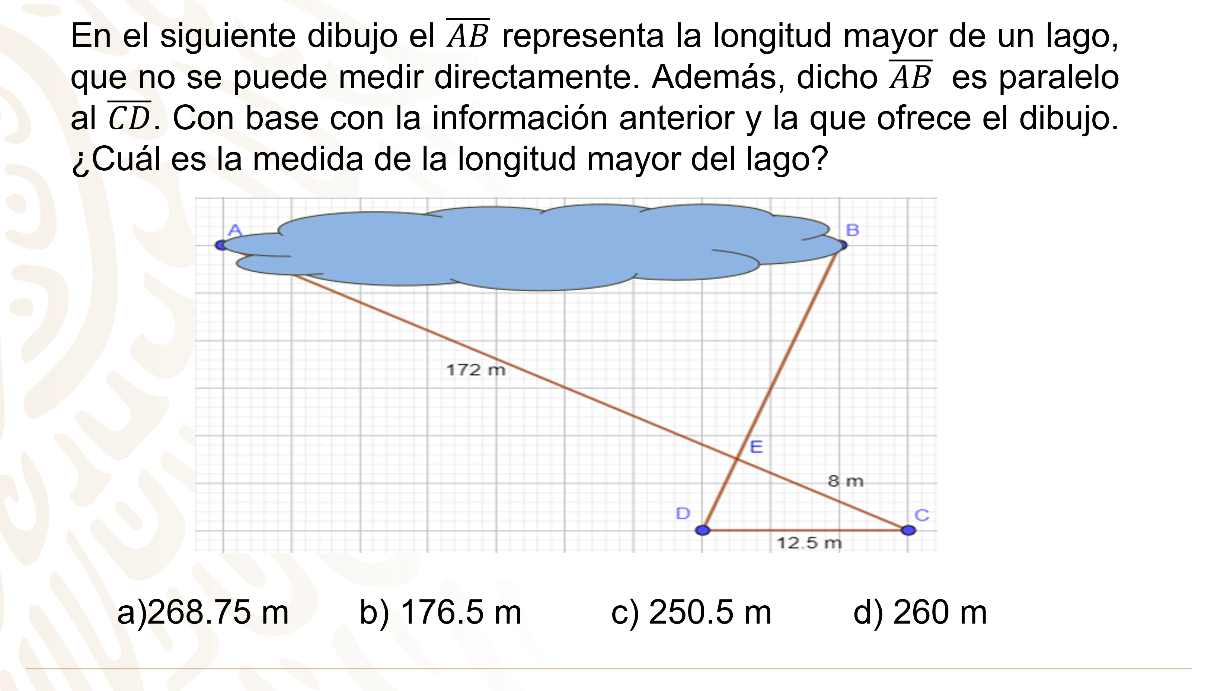
Al observar el dibujo, se trata de triángulos semejantes y las medidas ya se encuentran dentro de la figura, por tener bases paralelas, es posible aplicar el teorema de Tales.

Para expresar el teorema considera relacionar de forma correcta sus lados homólogos.

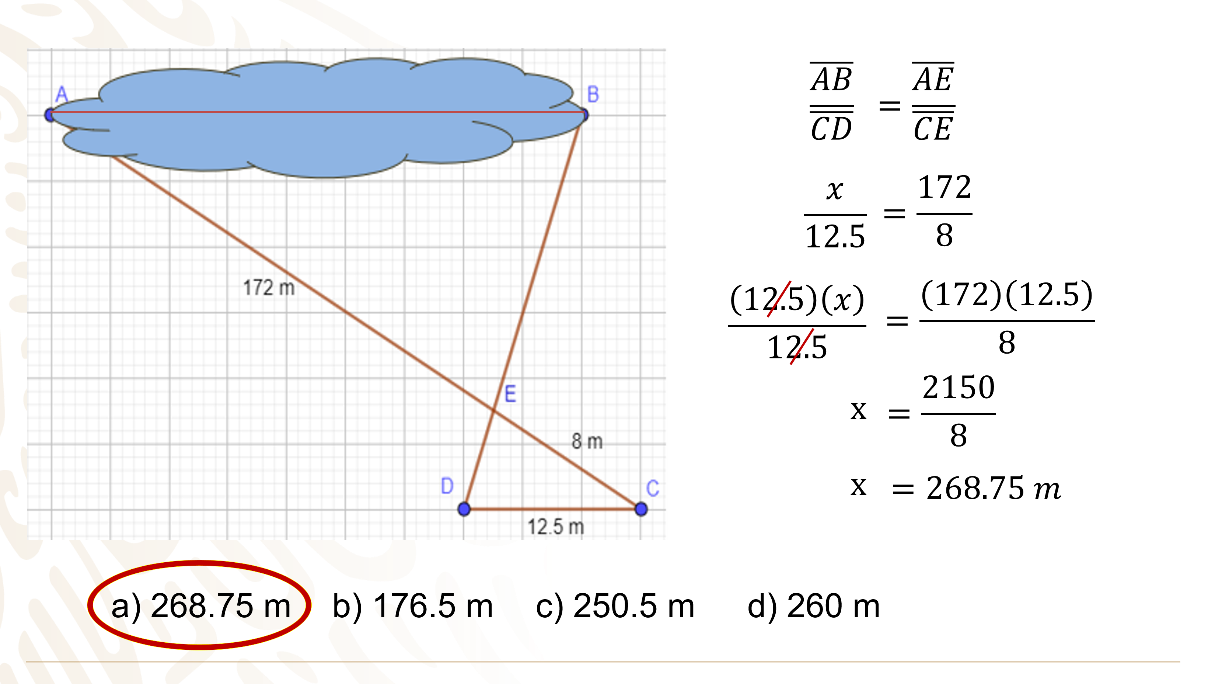
Se puede partir del segmento desconocido, es decir, el segmento “AB” entre su homologo el segmento “CD” es igual al segmento “AE” porque estás hablando del triángulo mayor entre el segmento “CE”.

Sustituyes valores y tienes que “x” entre 12.5 es igual a 172 entre 8, multiplicas por 12.5 en ambos miembros de la igualdad para despejar a “x” y realizas operaciones. Tienes que “x” es igual a 2150 entre 8 es igual a 268.75 m.

La respuesta correcta es el inciso a.

Realiza el siguiente ejercicio, pon atención a la lectura para comprender bien lo que pide el problema y así plantear y resolverlo.

Para el ejercicio que ahora te ocupa y siguiendo los pasos para resolver el ejercicio, primero debes entender lo que está planteando.

Lo que pide el ejercicio en sí es, saber cuál es el costo de la malla que se pondrá en la periferia del terreno que te dan, para eso como dato tienes, las longitudes de algunos lados del terreno, pero si te das cuenta en el croquis, hace falta la longitud de dos lados del terreno.

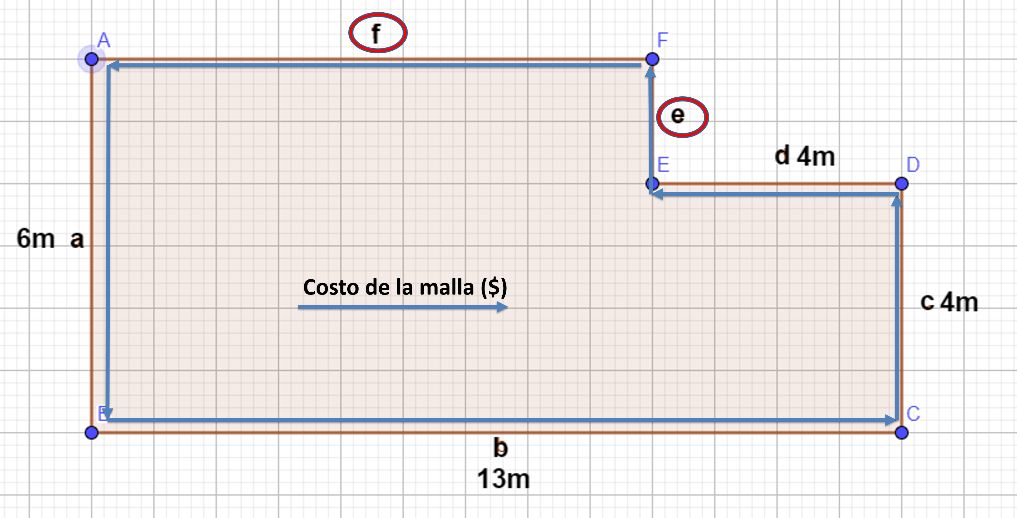
Por lo tanto, te ocuparás primero en determinar esas longitudes de los lados que faltan, Una vez determinados procederás a determinar el perímetro total del terreno que sería el dato principal que necesitas para saber el costo total, ya que harás una multiplicación de este perímetro total por el costo por metro lineal de la malla y con esto estarías contestando el problema.

Para determinar el perímetro del terreno, para ello se necesitan las longitudes de todos los lados, ya identificaste las primeras incógnitas, que denominan como (e) y (f) y son longitudes de los lados que se desconocen.

El cálculo del lado (e).

Los datos que tienes del terreno son:

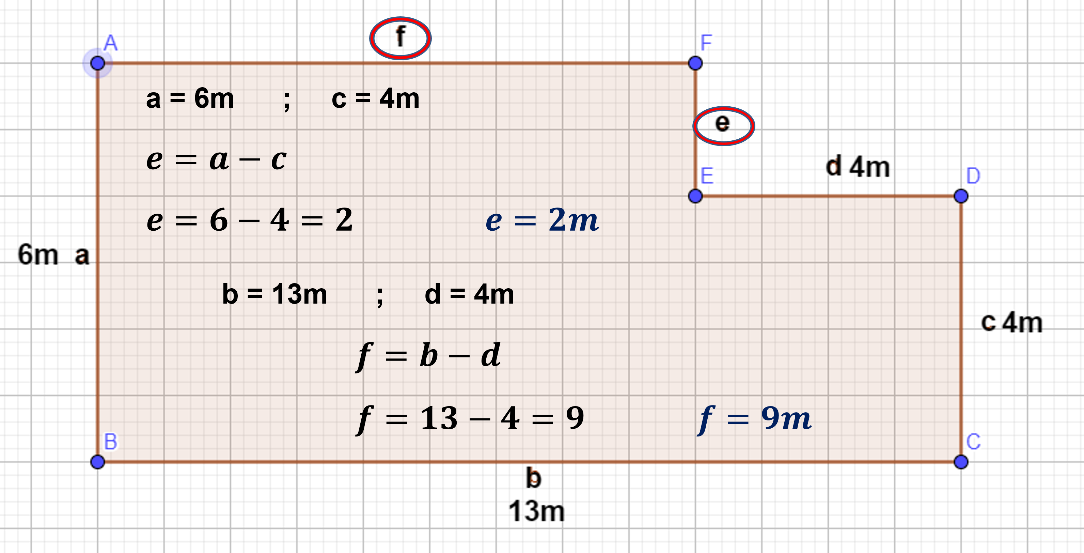
Longitud (a) = 6 metros.

Longitud (c) = 4 metros.

La longitud (e) es igual a la longitud del lado (a) menos la longitud del lado (c), por lo tanto:

Lado e es igual a 6 metros menos 4 metros

Lo que queda que la longitud del lado (e) es igual a 2 metros.

Ahora el cálculo del lado (f).

Para conocer la longitud el lado (f) necesitas la Longitud del lado (b) que es igual a 13 metros.

Longitud del lado (d) que es igual a 4 metros. entonces.

Longitud del lado (f) es igual a la longitud del lado (b) menos la longitud del lado (d).

Esto es, lado (f) es igual a 13 menos 4 igual a 9.

Longitud del lado (f) es igual a 9 metros.

Se concluye con esto que la longitud del Lado (e) es igual a 4 metros y La longitud del lado (f) es de 9 metros.

Con esto tienes ya todas las longitudes de los lados del terreno, que ahora observa en el croquis.

Así, ya puedes calcular el perímetro total del terreno, entonces.

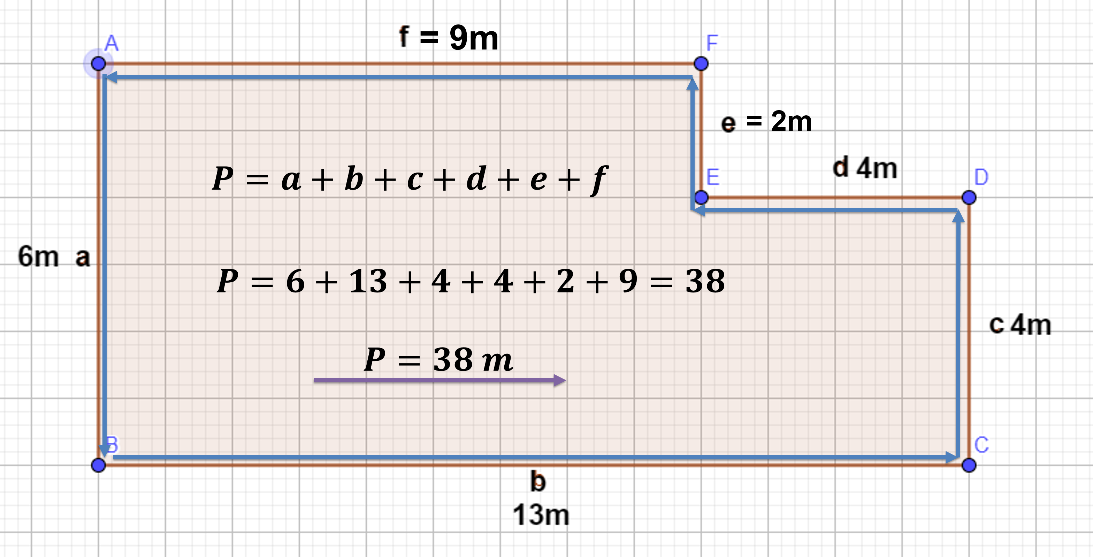
El perímetro del terreno se define como la suma de todos los lados del terreno.

Por lo tanto, tomando los datos de los lados.

El Perímetro del terreno es igual a “a” más “b” mas “c” más “d” más “e” mas “f”.

El perímetro del terreno es igual a 6 metros, más 13, más 4, más 4, más 2, más 9 metros.

Queda el perímetro igual a 38 metros.

Ahora, ya teniendo el perímetro del total del terreno, este es equivalente a la longitud total de la malla que se debe colocar en el mismo y por lo tanto con este perímetro calcularás el costo total de la malla correspondiente.

Para este proceso, ya tienes:

Perímetro igual a 38 metros.

Y el costo del metro lineal de malla es de: $58.50.

Entonces el costo total de la malla es igual a Perímetro total por Costo por metro lineal, y sustituyendo queda: Costo total igual a 38 metros por $58.50 pesos por metro lineal.

Queda Costo total igual a $2,223 pesos.

Observando las opciones que dan en el ejercicio la respuesta correspondiente al resultado que dio es la opción (d).

Analiza el siguiente ejercicio que mandó uno de los alumnos del interior del país, desde Mérida en el estado de Yucatán.

1. 10 m b)19 m c) 6 m d) 12 m

Para poder calcular el total del refuerzo a comprar necesitas saber cuál es la longitud del perímetro de la circunferencia superior e inferior de la cisterna.

Para eso primero necesitas obtener el radio de la cisterna ya que tienes presente que la circunferencia superior e inferior son iguales, para esto, emplearás la fórmula del volumen (V) de un cilindro de radio (r) y altura (h).

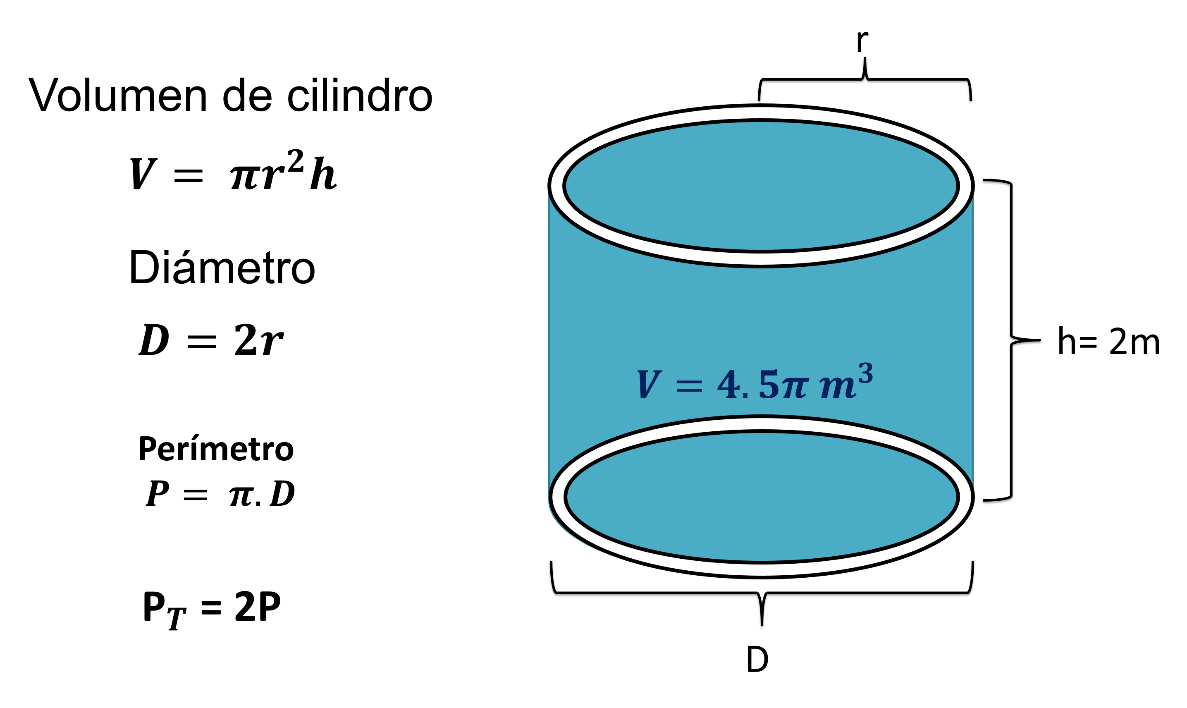
Una vez obtenido el radio de la circunferencia, obtendrás el diámetro de esta duplicando el radio.

Con el diámetro ya calculado, calcularás el perímetro de la circunferencia empleando la relación P= 2 por el diámetro de la misma circunferencia, y con el perímetro calculado lo duplicarás y aproximas el resultado al entero, obteniendo el resultado que se pide.

En este caso no necesitas calcular el Volumen porque es un dato que ya tienes en el ejercicio, pero si es un dato que, con la altura, te sirve para determinar el radio que te pide.

Para obtener el volumen del cilindro utilizarás la fórmula.

V = π.r².h

Y según los datos que el ejercicio da tienes que:

Volumen (V) = 4.5 π metros cúbicos.

Altura (h) = 2 metros

Radio (r) es la incógnita que determinarás.

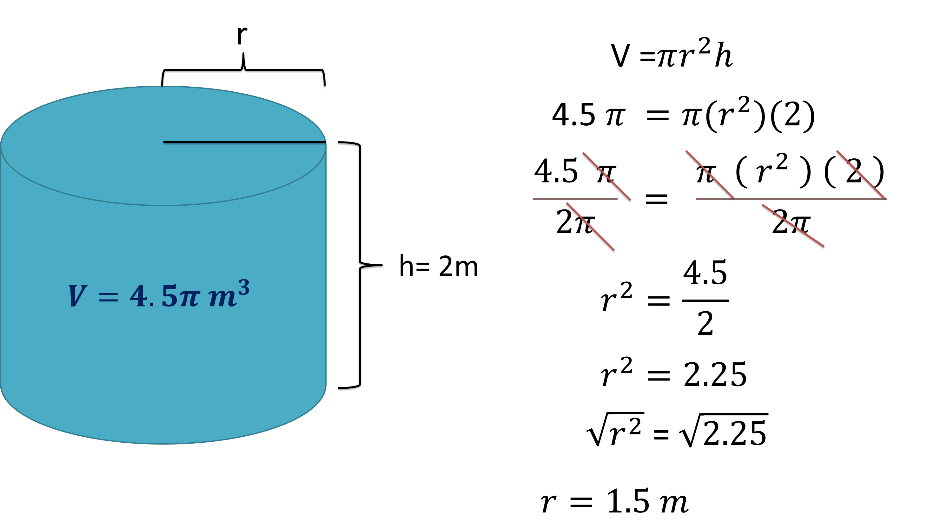
Puedes hacer la sustitución de los valores que te dan para despejar posteriormente la incógnita que necesitas calcular, o también puedes despejar la incógnita que necesitas calcular y posteriormente sustituir los valores que te proporcionan.

En este caso primero se hace la sustitución de los datos y después despejas la incógnita que debes calcular.

Entonces tomando la expresión, tienes que.

4.5 pi es igual a pi por radio al cuadrado por 2

Divides por 2 π a ambos miembros de la expresión.

4.5 por pi entre 2 pi es igual a pi por radio al cuadrado por 2 entre 2 por pi.

Se eliminan pi en el primer miembro, 2 y pi en el segundo miembro de la expresión y reagrupando queda.

Radio al cuadrado igual a 4.5 entre 2, igual a 2.25

Extraes una raíz cuadrada a ambos miembros de la expresión, quedando:

Radio es igual a la raíz cuadrada de 2.25, es igual a 1.5 metros

Hasta aquí ya tienes calculado el radio de la cisterna, ahora ve al cálculo del perímetro, siguiendo el planteamiento que hiciste al principio.

Si ya tienes el radio (r) = 1.5 metros., entonces:

El diámetro será el doble de ese radio, por lo tanto

Diámetro es igual a 2 por 1.5 igual a 3 metros.

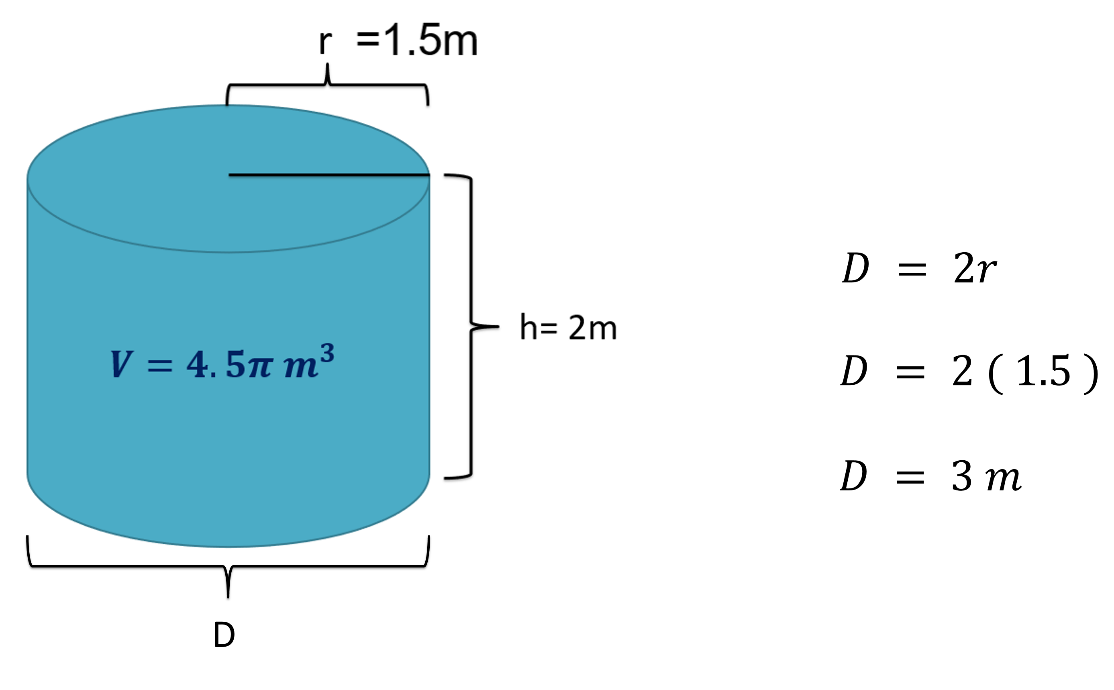
Ahora que ya tienes el diámetro, determina el perímetro de la circunferencia, y para eso emplearás la expresión:

Perímetro igual a dos veces el diámetro

Si el diámetro es igual a 3 metros y el valor de pi ya lo conoces, entonces sustituyes y queda.

P igual a pi por 3. Y queda igual a 9.42 metros.

Pero necesitas el perímetro de la circunferencia superior e inferior, por lo tanto, duplicarás el resultado obtenido.

Perímetro total igual a 2 por 9.42 igual a 18.84

Perímetro total igual a 18.84 metros.

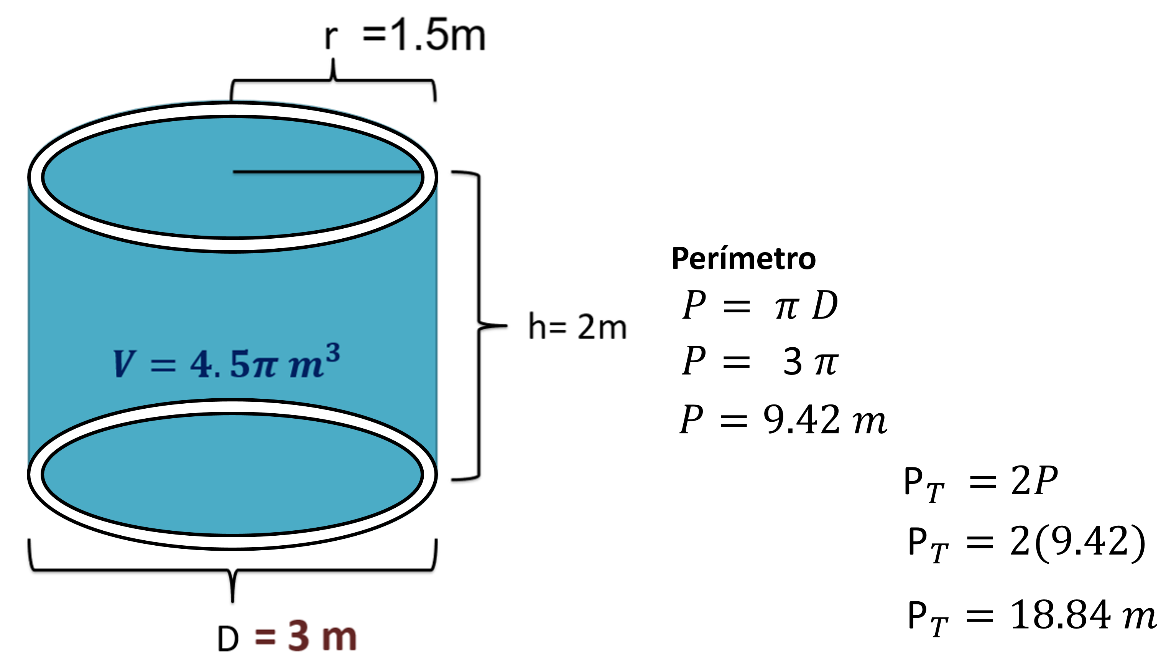
Y como el perímetro total es equivalente a la cantidad total del refuerzo que se necesita comprar entonces, redondeas la cantidad obtenida al entero más próximo que es.

Perímetro total igual a 19 metros.

Por lo tanto, la respuesta correcta es el inciso (b).

Ahora analiza otro ejercicio.

Para poder determinar el área y así la cantidad de pasto que se requiere para cubrir el área, se debe obtener el área del círculo mayor y se le resta el área del cirulo menor.

Pero para calcular esas áreas, necesitas de los radios de cada circulo y no se tienen directamente, por lo que obtendrás dichos radios a partir de la información que se da.

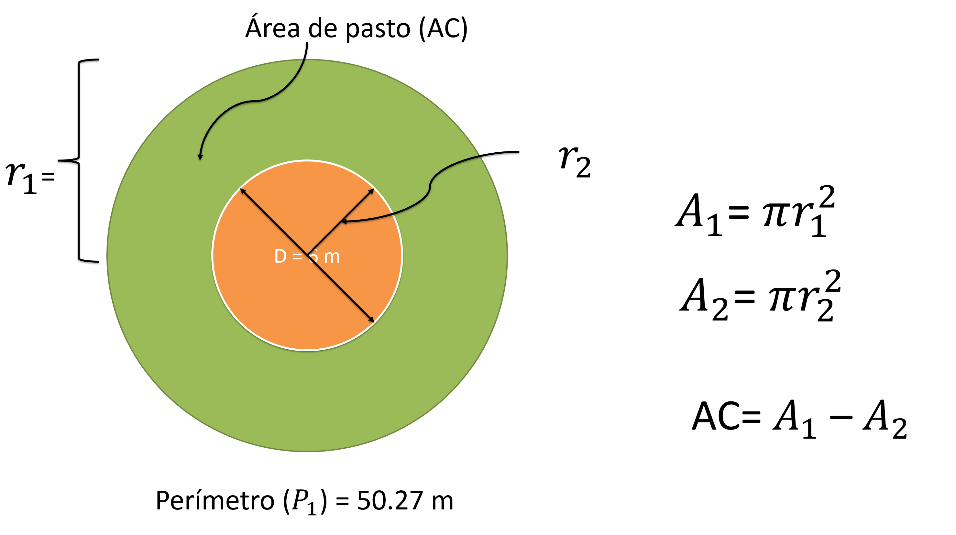
Para el radio del círculo mayor(r1), dan el perímetro de la circunferencia de dicho circulo, que es P1 = 50.27 m y utilizarás la fórmula de la relación Pi igual a perímetro entre Diámetro.

Perímetro igual a 50.27 metros. Que despejando D en la fórmula queda:

D igual a P1 entre Pi, sustituyendo el perímetro queda.

Diámetro igual a 50.27 entre Pi, igual a 16 metros.

Ya obtenido el diámetro procederás a encontrar el radio.

Radio es igual a 16 metros entre 2, igual a 8 metros.

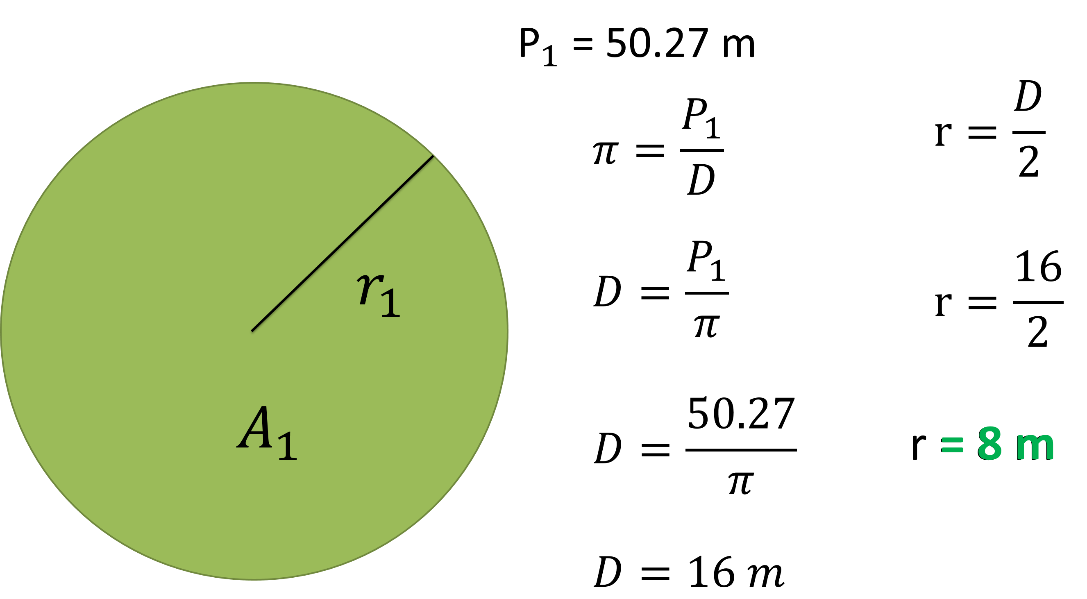
Ahora calcula el radio del círculo menor.

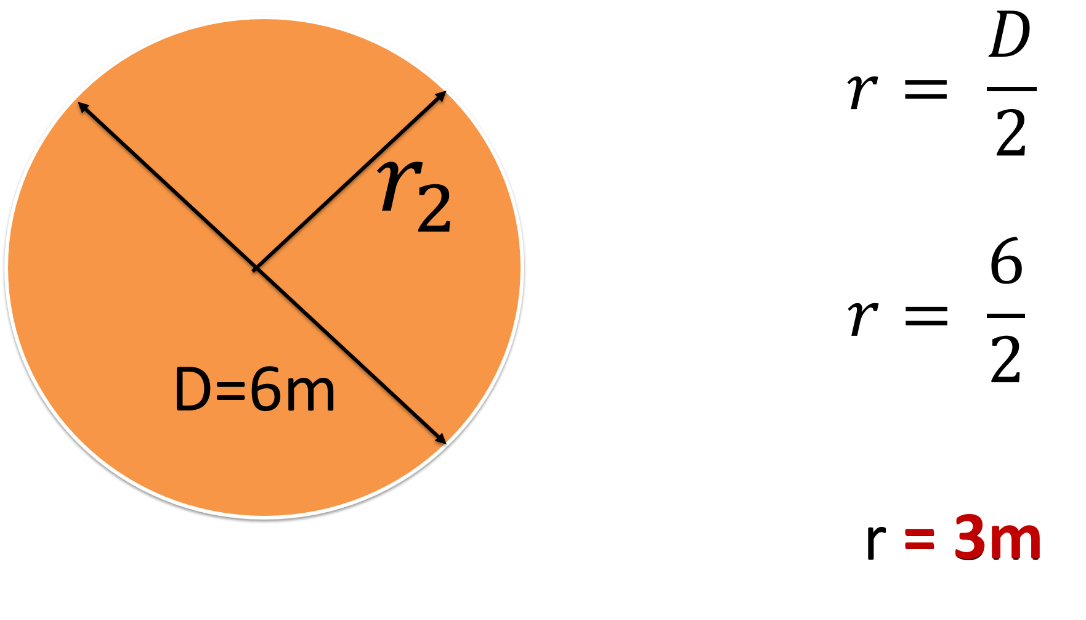
Para esto te dan el diámetro del círculo menor que es:

Diámetro igual a 6 metros.

Divide el diámetro entre 2, es decir 6 entre 2 igual a 3 metros.

El radio del círculo menor es de 3 metros.

Ya teniendo los radios de los dos círculos, calcula el área de cada uno de ellos.

Al área del círculo mayor lo llamarás Área uno.

Al radio de este círculo mayor lo llamarás radio 1.

Entonces el área A1 es igual a pi por el radio 1 al cuadrado.

Sustituyendo los datos en la fórmula, tienes:

Área 1 igual a pi por radio 1 al cuadrado. Sustituyendo:

Es igual a pi por 8 al cuadrado, igual a pi por 64, es igual a 201.06 metros cuadrados.

Ya tienes el área del primer círculo, ahora calcula el área del círculo menor.

Esta área la llamarás Área 2.

Al radio de este círculo menor lo llamarás radio 2

Entonces el área A2 es igual a pi por el radio 2 al cuadrado.

Sustituyendo los datos en la fórmula, tienes:

Área 2 igual a pi por radio 2 al cuadrado. Sustituyendo

es igual a pi por 3 al cuadrado, igual a pi por 9, es igual a 28.27 metros cuadrados.

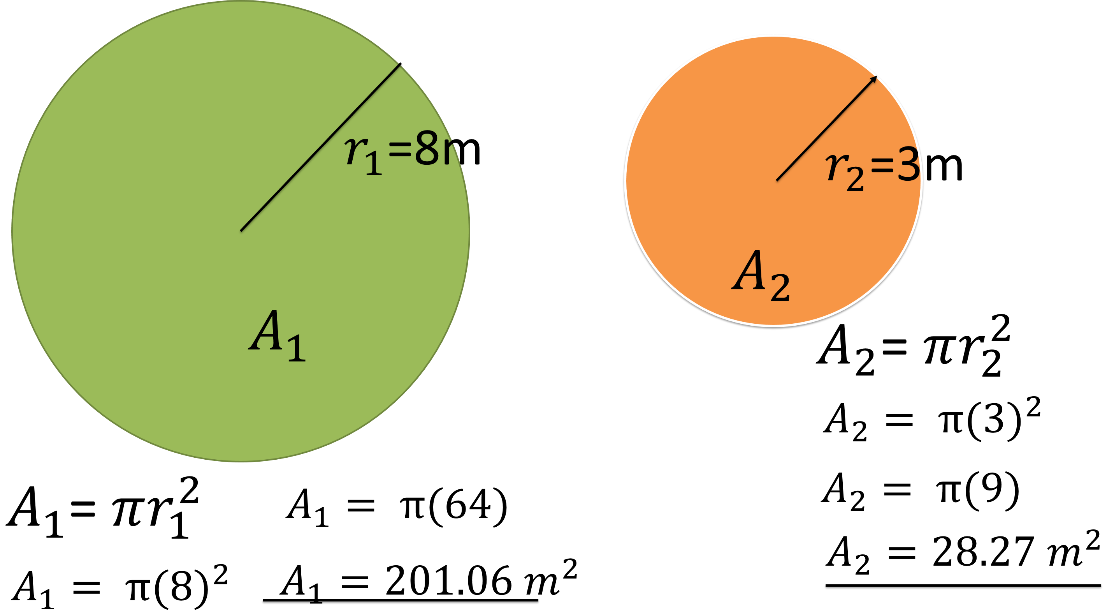
Ya que tienes las áreas de los dos círculos, ahora calcularás el área comprendida entre los dos.

Eso se obtiene restándole al área mayor A1 el área menor A2, y le llamarás área de la corona.

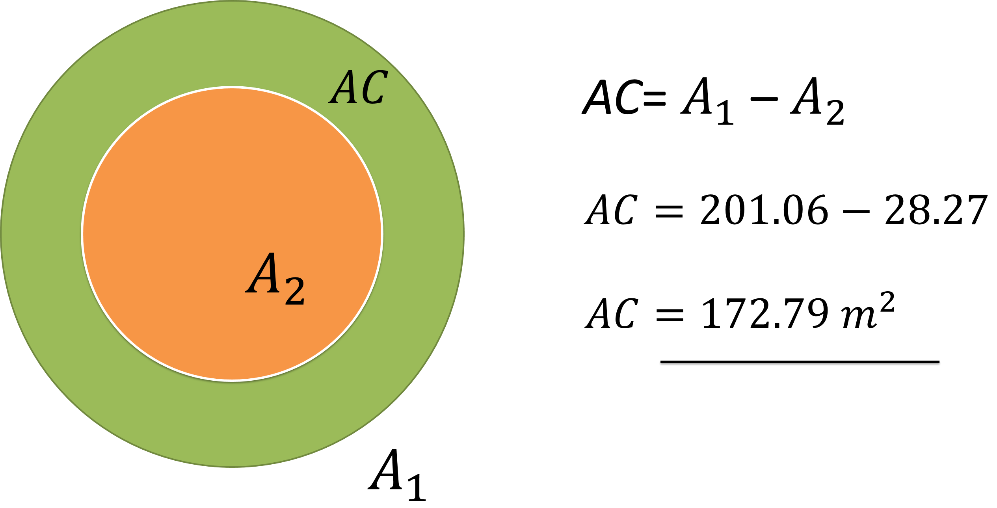
Área de la corona igual área 1 menos área 2. Sustituyendo los datos.

Área de la corona igual 201.06 menos 28.27, igual 172.79 metros cuadrados.

El área delimitada entre los dos círculos concéntricos es de 172.79 metros cuadrados. Y por lo tanto la cantidad de pasto a colocar en ese jardín es la misma.

Según este resultado la opción correcta es el inciso (d).

El reto de hoy:

Realiza los siguientes ejercicios, el primero es:

Segundo ejercicio:

Este tipo de ejercicios se parecen a las pruebas estandarizadas para ingresar a las preparatorias, así como las pruebas de ingreso a la licenciatura o universidad.

Sigue practicando para alcanzar confianza y habilidad en los que se te presenten.

Albert Einstein decía: “Lo importante es no dejar de hacerse preguntas”.

Entonces continúa enfrentando retos y estrategias de solución.

¡Buen trabajo!

Gracias por tu esfuerzo.

*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.