Resolución de problemas de conversiones de unidades en el Sistema Internacional de Unidades y el Sistema Inglés

Resolución de problemas de conversiones de unidades en el Sistema Internacional de Unidades y el Sistema Inglés

Aprendizaje esperado: resuelve problemas que implican conversiones de unidades del Sistema Inglés (yarda, pulgada, galón, onza y libra).

Énfasis: dar sentido y significado a la resolución de problemas que implican conversiones de unidades de longitud.

¿Qué vamos a aprender?

Continuaras profundizando en el Sistema Internacional de Unidades y en el Sistema Inglés. En esta sesión, analizarás y le darás tanto sentido como significado a la resolución de problemas que implican conversiones de unidades de longitud.

¿Qué hacemos?

Antes de iniciar con la resolución de problemas, analiza la siguiente información.

El movimiento rectilíneo uniforme, es aquel con rapidez constante y cuya trayectoria es en línea recta. Un ejemplo claro son las puertas correderas de un ascensor, generalmente se abren y cierran en línea recta y siempre a la misma velocidad.

Ahora, reflexiona en la siguiente pregunta y resuelve.

Problema 1

¿Cuántos metros por segundo requiere un auto de carreras para recorrer 45km en un cuarto de hora?

Los autos de carreras corren en circuitos, y no hay circuitos que tengan rectas de 45 kilómetros, por ello, considera que el escenario en el que corre el auto de carreras es una línea recta.

Los datos son los siguientes:

Distancia (d) = 45 kilómetros.

Tiempo (t) = un cuarto de hora.

Como la relación que se busca es metros por segundo, esto lleva a que la incógnita es la velocidad. ¿Conoces la fórmula de la velocidad? La fórmula es la siguiente:

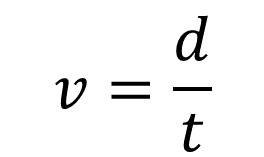
Toma un momento para pensar en las respuestas de estas preguntas: ¿cuántos metros deberá recorrer en un segundo?, ¿cómo se resuelve?

Una de las varias maneras de resolver el problema es, primero convertir 45 kilómetros a metros. Para ello, apóyate de lo que ya sabes: 1 kilómetro equivale a 1,000 metros. Entonces, en 45 kilómetros hay 45,000 metros.

Ahora, puedes continuar con la conversión del tiempo, es decir, convertir un cuarto de hora a su equivalente en segundos. Una forma de hacerlo es tener en cuenta que 1 hora tiene 60 minutos. Entonces, un cuarto de hora tiene 15 minutos. ¿Cómo se obtiene este resultado? Una forma es dividiendo 60 entre 4

Después, se puede considerar que 1 minuto tiene 60 segundos. Entonces, 15 minutos equivalen a 900 segundos. ¿Cómo se obtiene este dato? Una forma es multiplicar 15 por 60. De esta manera, se puede afirmar que un cuarto de hora es igual a 900 segundos.

Reflexiona: ¿qué se hace con las equivalencias obtenidas para resolver el problema?

Ya se cuenta con los datos en las unidades que las condiciones del problema solicitan, la distancia es igual a 45,000 metros, el tiempo igual a 900 segundos y la velocidad sigue siendo la incógnita. Por lo tanto, utilizarás la fórmula de la velocidad del movimiento rectilíneo uniforme:

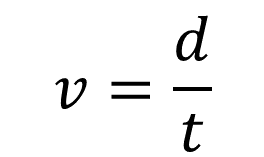
Donde:

d = 45,000 m

t = 900 s

v = ¿?

Sustituyendo valores y resolviendo, se obtiene lo siguiente:

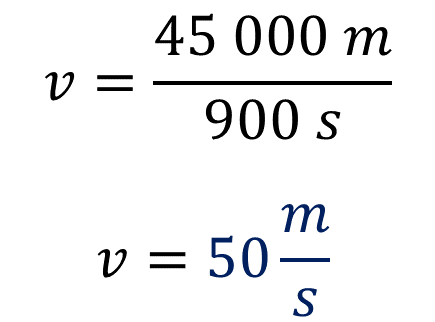
El resultado es 50 metros sobre segundo. Por lo tanto, con una velocidad de 50 metros por segundo, el auto de carreras recorrerá 45 kilómetros en un cuarto de hora.

Continúa con el siguiente problema para seguir con las conversiones de unidades.

Problema 2

A un ingeniero le encargaron enmallar una bodega rectangular que mide 163 metros de largo y 60 metros de ancho. Le pidieron que lo hiciera con un tipo de malla que no encontró en el país.

Al buscar en internet, encontró esa malla en una tienda de Estados Unidos. Ahí se vende la malla en rollos con 100 yardas (yd) y 2 pies (ft). Si necesita comprar la malla en esa tienda, ¿cuántos rollos debe adquirir?

Resuelve el problema. La bodega tiene forma rectangular, el largo será la base y el ancho la altura. La base de la bodega es de 163 metros y la altura de 65 metros.

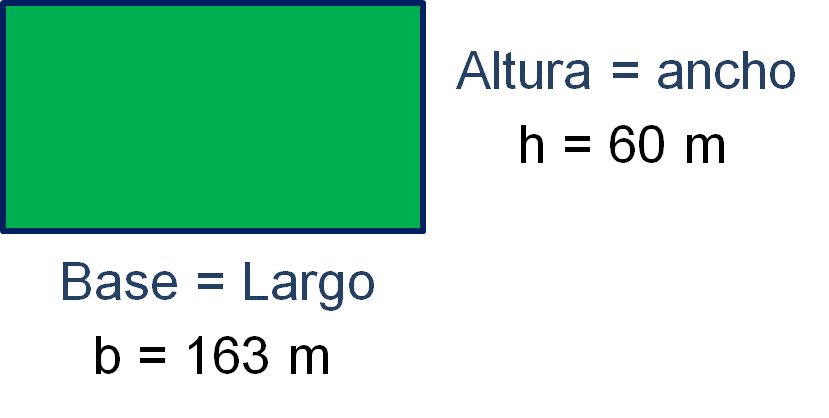
Una forma de iniciar la resolución del problema es determinar el perímetro de la bodega. ¿Para qué sirve calcular la medida del perímetro de la bodega? El perímetro de la bodega determina la cantidad de malla que el ingeniero deberá adquirir.

Se puede calcular el perímetro del terreno rectangular usando la siguiente fórmula:

Como la base mide 163 metros y la altura mide 60 metros, al sustituir estos valores en la fórmula se tiene:

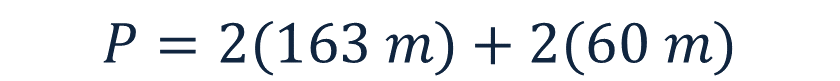
De acuerdo con la jerarquía de las operaciones, primero debes resolver las multiplicaciones, por lo tanto:

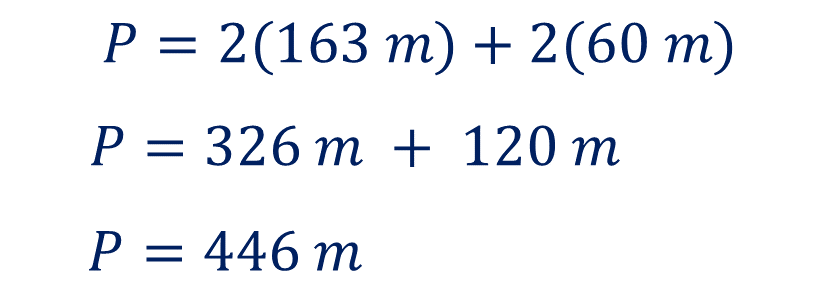
El perímetro de la bodega rectangular es de 446 metros. Se determina que esa es la cantidad de malla que necesita el ingeniero para hace su trabajo. ¿Cómo continuas en la resolución de este problema?

Una manera de continuar con la resolución del problema es convertir a metros el contenido de los rollos de malla. Una yarda equivale a 0.9144 metros, y lo que se necesita es determinar la equivalencia en metros, de 100 yardas.

1 yd = 0.9144

100 yd = x

¿Qué harías para calcular el valor de “x”? Una forma de calcular el valor de “x” es multiplicar el número de yardas, que es 100, por su equivalente en metros, es decir, 0.9144 metros, todo esto sobre 1 yarda. Al resolver esta multiplicación se obtienen 91.44 metros.

Continúa con la siguiente conversión. Una manera de realizar esta conversión es partir de la equivalencia entre 1 pie y el metro. De esta forma se tiene que 1 pie es igual a 0.3048 metros.

1 ft = 0.3048

Entonces, ¿qué se puede hacer para determinar el equivalente, en metros, de 2 pies? Como 1 pie es equivalente a 0.3048 metros, entonces, 2 pies será igual a 2 por 0.3040 metros, es decir, 0.6096 metros.

Ahora, ya que cuentas con las medidas de 100 pulgadas y 2 pies en metros, ya puedes calcular el contenido en metros, del rollo de malla. Como el rollo contiene 100 yardas y 2 pies de malla, entonces, la cantidad, en metros, será la suma de las equivalencias obtenidas.

100 yd + 2 ft

91.44 m + 0.6096

La suma de estas medidas es de 92.0496 metros, que corresponde al contenido del rollo de malla.

Ahora, el problema dice que, si el ingeniero necesita comprar la malla en esa presentación, ¿cuántos rollos debe adquirir?

Reflexiona: ¿qué harías para saber cuántos rollos de malla debe comprar el ingeniero?

Se puede interpretar la solución como el número de veces que cabe el contenido de un rollo de malla en el perímetro del terreno rectangular. De esta manera, se tiene la división de 446 metros entre 92.0496 metros. El cociente obtenido es aproximadamente 4.845213885 y al redondear a dos decimales el resultado es 4.85 aproximadamente.

Entonces, ¿cuántos rollos de malla debe comprar? El ingeniero debe adquirir 5 rollos de malla para poder realizar el trabajo que le ha sido encargado.

A continuación, resuelve otro problema.

Problema 3

En un aeropuerto de Estados Unidos se anuncia que el volumen máximo permitido que los pasajeros necesiten subir con ellos es de 4,800 pulgadas cúbicas. En caso de exceder este volumen, se debe pagar una cantidad extra.

Julia quiere llevar con ella una maleta de 80 centímetros de largo, 52 centímetros de ancho y 22 centímetros de grueso. ¿Deberá pagar Julia por exceso de volumen?

Una forma de iniciar la resolución del problema es representar la maleta de la siguiente manera.

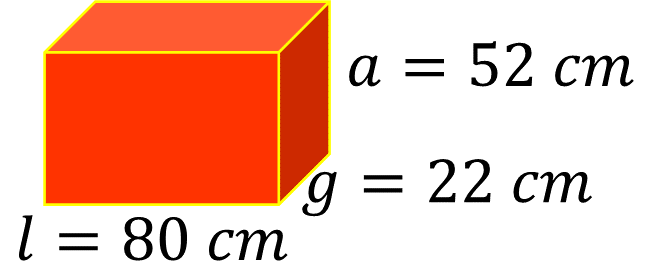
Entonces, ¿cómo se calcula su volumen en pulgadas cúbicas? Como el volumen permitido para no pagar exceso de equipaje está dado en pulgadas cúbicas, entonces puedes convertir las medidas de la maleta dadas en centímetros en sus equivalentes, pulgadas.

Reflexiona en lo siguiente: si 1 pulgada equivale a 2.54 centímetros, entonces al convertir 80 centímetros a pulgadas, se deben obtener más de 80 o menos de 80 pulgadas, ¿por qué?

Al ser la pulgada una longitud mayor que el centímetro, cuando se convierten 80 centímetros a pulgadas se deben obtener menos de 80. Ahora, con tu calculadora o a mano, realiza la conversión de 80, 52 y 22 centímetros que son las magnitudes de la maleta a sus equivalentes en pulgadas.

En este caso, una manera de encontrar las equivalencias de las longitudes que se tienen en centímetros es dividir la cantidad de centímetros entre 2.54. Entonces, al dividir 80 entre 2.54 se obtiene 31.496, que son las pulgadas que equivalen a 80 centímetros.

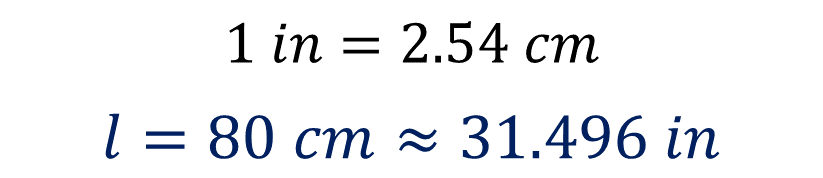
Después, se divide 52 entre 2.54. De esta manera se obtiene 20.472. Que es equivalente, en pulgadas, de 52 centímetros.

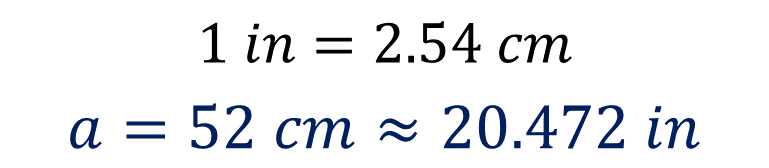
Por otro lado, cuando se divide 22 entre 2.54 se obtiene 8.661, que es el equivalente, en pulgadas, de 22 centímetros.

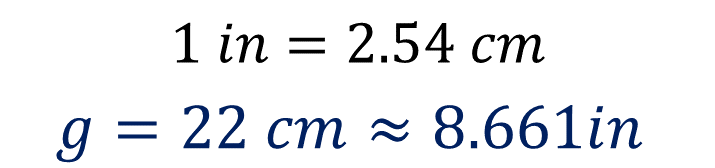
Ya tienes las medidas aproximadas de la maleta en pulgadas. Ahora, utilizarás la fórmula para calcular el volumen de un paralelepípedo, que es un cuerpo geométrico como el que representa a la maleta. Volumen es igual al largo por el ancho por el grueso.

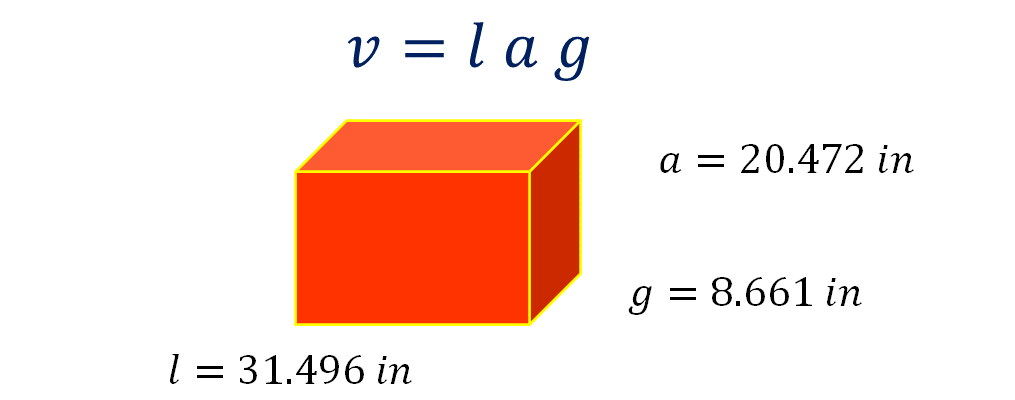
Al sustituir las medidas en la fórmula anterior se tiene:

Por lo tanto, se obtiene 5,584.49 pulgadas cúbicas aproximadamente.

Ahora, ya puedes dar solución al problema. Como el volumen máximo permitido para no pagar una cuota extra es de 4,800 pulgadas cúbicas y el volumen de la maleta de Julia es de 5,584 pulgadas cúbicas, se puede afirmar que, si Julia quiere llevar su maleta con ella, deberá pagar una cuota extra.

Ya observaste, en los tres primeros problemas, la importancia de tener las unidades en un mismo sistema, lo que permite resolver diversas situaciones en ciencias como la física. Esto es relevante para poder comprender temas como velocidad, aceleración, fuerza, densidad y presión.

Ahora, resuelve el siguiente problema.

Problema 4

Una caja de loseta vinílica contiene 45 piezas. Si las dimensiones de una loseta son de 1 pie (ft) de largo y 5 pulgadas (in) de ancho. ¿Cuántas cajas de loseta se requieren comprar para cubrir el piso de una recámara de 12 metros cuadrados?

Resuelve el problema. La loseta es de forma rectangular, el largo del rectángulo será la base y el ancho la altura. La base de la loseta es de un pie y la altura de 5 pulgadas.

Por otro lado, como lo que se quiere es cubrir la superficie de una recámara, entonces considera el área de la loseta. La fórmula que permite calcular el área de un rectángulo es área igual a base por altura.

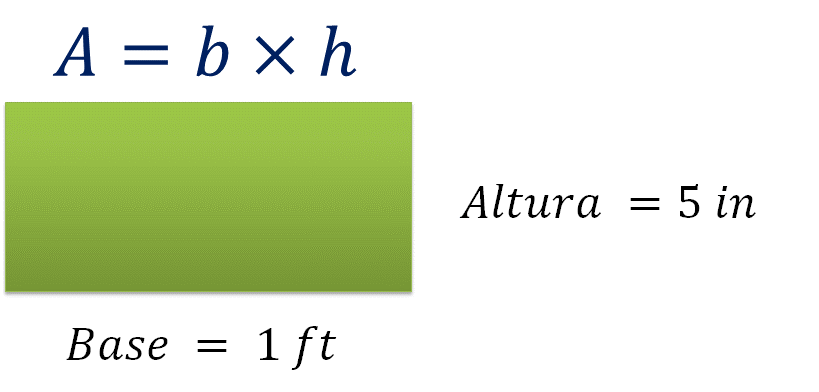
Además, como el área de la recámara está dada en metros cuadrados, se necesitan convertir las medidas de la base y de la altura.

Lo primero que harás es convertir la medida de la base al sistema internacional de medidas. Por lo tanto, como un pie es equivalente a 0.3048 metros, ésta es la medida de la base del rectángulo.

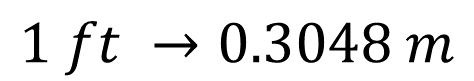
La altura es igual a 5 pulgadas y lo convertirás a metros. Una manera de realizar conversiones es determinar el factor de equivalencia. En este caso, el factor de equivalencia es: una pulgada es igual a 0.0254 metros.

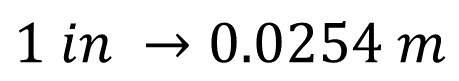
Con ello, puedes usar la proporción: una pulgada es a 5 pulgadas como 0.0254 metros es a “x”, donde “x” representa la medida, en metros, equivalente a 5 pulgadas.

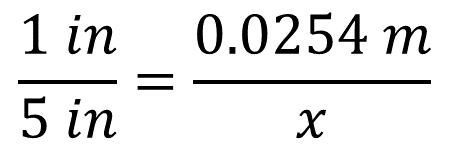
Para determinar el valor de x, multiplica 5 pulgadas por 0.0254 metros y divide el producto obtenido entre una pulgada.

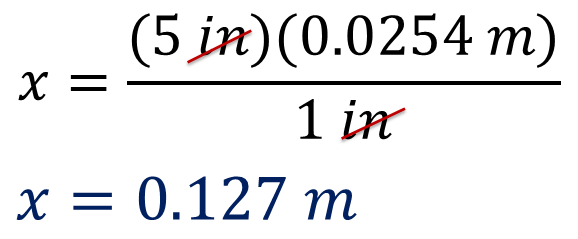
El resultado es de 0.127 metros.

Ya que se convirtieron las medidas de la base y la altura a metros, procede a determinar el área de una loseta. Utiliza la siguiente fórmula:

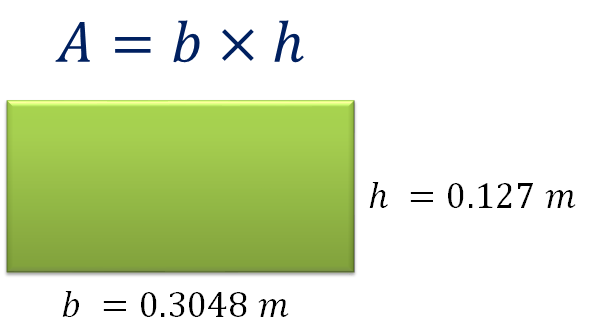
Sustituye los valores en la fórmula:

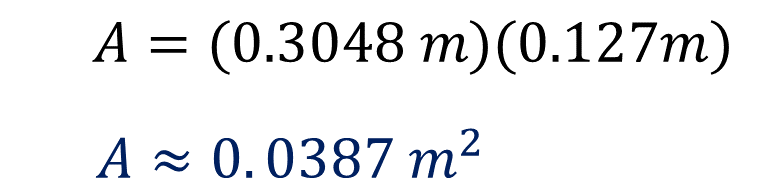
Se obtiene que el área de una loseta es igual a 0.0387 metros cuadrados, aproximadamente.

Una manera de continuar con la resolución del problema es calcular la superficie que se puede cubrir con las losetas contenidas en una caja.

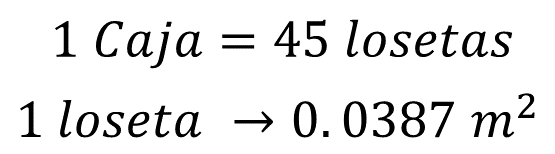
Una loseta tiene un área de 0.0387 metros cuadrados, este valor es el factor de equivalencia. Con ello, se establece la proporción: una loseta es a 0.0387 metros cuadrados como 45 losetas es a “x”, donde “x” es el área que se puede cubrir con el contenido de una caja de losetas.

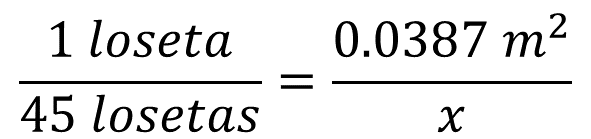
Para determinar el valor de “x”, se multiplican 45 losetas por 0.0387 metros cuadrados y se divide el producto obtenido entre una loseta.

Por lo tanto, se obtiene 1.7415 metros cuadrados. Entonces, con el contenido de una caja de losetas se puede cubrir una superficie de 1.7415 metros cuadrados. Al redondear a dos decimales el resultado es 1.74 metros cuadrados, se redondea hacia abajo con la idea de que sobre material en lugar de que falte.

Para finalizar, calcula cuántas cajas se deben comprar para cubrir el piso de una recámara de 12 metros cuadrados. Se sabe que con las losetas contenidas en una caja se cubre un área de 1.74 metros cuadrados, este valor será el factor de equivalencia.

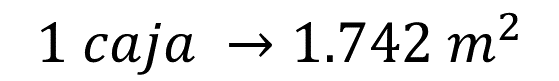
Con ello, se establece la proporción: una caja es a 1.742 metros cuadrados como “x” es a 12 metros cuadrados.

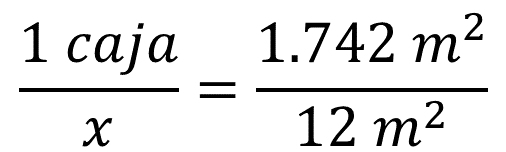
Para determinar el valor de “x”, que representa el número de cajas a comprar, se multiplican 12 metros cuadrados por una caja y se divide el producto obtenido entre 1.742 metros cuadrados.

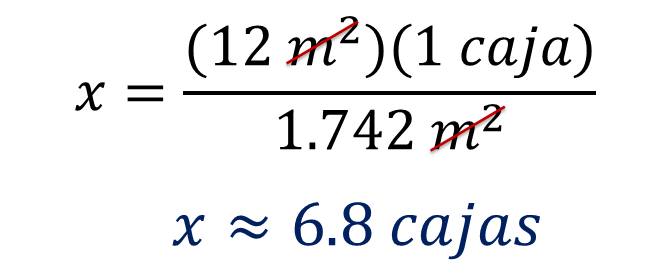
El resultado aproximadamente es de 6.8 cajas. Como no es posible comprar 6.8 cajas, se puede afirmar que se necesitan comprar 7 cajas de loseta para cubrir el piso de una recámara de 12 metros cuadrados.

Con esto has concluido. En esta sesión analizaste y resolviste algunos problemas que implican conversiones de unidades de longitud.

El reto de hoy:

Piensa en algunas situaciones problemáticas cuya resolución necesite realizar conversiones entre las unidades de longitud del Sistema Internacional y del Sistema Inglés.

Además, resuelve algunos de los problemas o ejercicios sobre conversiones de unidades de longitud, de tu libro de texto de Matemáticas de segundo grado.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/