Representación de fenómenos físicos
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:23
Representación de fenómenos físicos
Aprendizaje esperado: lee y representa, gráfica y algebraicamente, relaciones lineales y cuadráticas.
Énfasis: representar diferentes situaciones y fenómenos de la Física.
¿Qué vamos a aprender?
Es importante que, conforme se vayan presentando las distintas actividades y ejercicios, vayas realizándolas, así como anotar en tu cuaderno lo que aprendes, además de tus dudas en torno a esta sesión
Te pedimos tener a la mano tu cuaderno, regla, lápiz o bolígrafo y lápices de colores.
Para el desarrollo de esta sesión es importante tener presente que: en una ecuación lineal, sus variables están elevadas a la primera potencia.
Así, una ecuación lineal puedes escribirla de la siguiente manera: ax+by=c.
¿Qué hacemos?
Cuando graficas una ecuación lineal en el plano cartesiano, obtienes una línea recta. Observa algunos ejemplos de gráficas de ecuaciones lineales.
En la primera imagen, tienes una gráfica en la que puedes observar una línea recta que presenta un crecimiento ascendente; en la segunda gráfica, la línea recta se comporta de manera descendente.
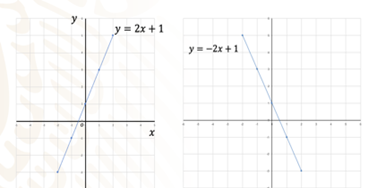
Una ecuación lineal también la puedes escribir como: y=mx+b; en este caso, tienes a las dos variables, “x” y “y”, elevadas a la primera potencia, y a las constantes “m” y “b”: "m" representa la razón de cambio entre dos coordenadas, y dice qué tan inclinada está la línea recta; y “b” es la ordenada al origen, es decir el punto en donde la línea recta corta al eje de las “yes”.
También en esta misma forma de ecuación lineal, puedes localizar a la variable dependiente “y” y a la variable independiente “x”.
¿Cuál es la expresión general de una ecuación cuadrática? Una ecuación cuadrática es aquella que tiene como expresión general la forma:
ax^2+bx+c=0
En donde a, b y c son constantes, y “x” es la variable independiente.
También ten presente que la gráfica asociada a una relación cuadrática es una curva llamada "parábola".
Aquí tienes un par de gráficas que representan ecuaciones de segundo grado.
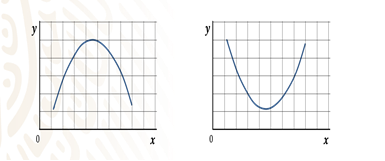
¿En qué se diferencian estas dos parábolas? En que la primera se abre hacia abajo, y la segunda hacia arriba.
¿Y qué dices de sus vértices?, ¿qué es el vértice de una parábola?
En una parábola, un vértice es el punto que corresponde al menor o al mayor valor que toma la ordenada. Es decir, es el punto de inflexión o cambio de la parábola.
Y entonces, ¿qué puedes decir de los vértices de ambas parábolas?
Que el vértice de la parábola que se abre hacia arriba ¡está abajo! y el vértice de la parábola que se abre hacia abajo en la segunda ¡está arriba!
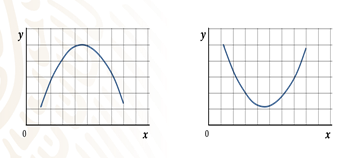
Hasta aquí, has revisado las características más importantes de las ecuaciones lineales y de las ecuaciones cuadráticas.
Ahora conocerás cómo este tipo de ecuaciones pueden ayudarte a resolver problemas cercanos a la vida real, particularmente en el ámbito de estudio de la Física.
Existen infinidad de situaciones en la Física que pueden ser representadas algebraicamente para poder darles una solución. Estas situaciones pueden presentar variaciones lineales, en cuyo caso, al graficar, obtendrás una línea recta o variaciones cuadráticas, en las cuales sus soluciones, al ser representadas en una gráfica, generan una curva denominada parábola.
¿Te gusta la astronomía? Sorprende cómo es que los astrónomos puedan saber tanto del universo. Esto es porque hacen cálculos matemáticos y utilizan muy frecuentemente ecuaciones lineales o cuadráticas. Observa algunos ejemplos.
¿Sabes quién fue Edwin Hubble? Fue el astrónomo que dedujo que las galaxias se separan unas de otras.
En 1921, Edwin Hubble midió las velocidades de algunas galaxias cercanas; notó que, al graficar la velocidad de las galaxias contra su distancia, los puntos que representaban cada una de las galaxias de su muestra, parecían seguir una línea recta creciente. Observa una gráfica representativa:

¿Qué significa esa línea recta creciente en la gráfica de los datos obtenidos por Hubble?
Hubble, a partir de los datos recabados durante años, dedujo que esa línea recta creciente significaba que, a mayor distancia a la que se encuentra una galaxia de la Tierra, más rápido se aleja; y no sólo eso, como ninguna galaxia es realmente el centro del universo, esto implica finalmente que todas las galaxias se alejan unas de otras.
La ecuación que describe esta ley, conocida como la ley de Hubble, se escribe de la siguiente manera: V = Hd.
Donde v es la velocidad que se quiere calcular, d la distancia al observador, y H el valor de la constante de Hubble.
La ecuación que representa a la Ley de Hubble es una ecuación lineal, porque está elevada a la primera potencia y su gráfica, es una línea recta.
Ahora, para determinar el valor de la constante de Hubble, "H", que en realidad es la constante de proporcionalidad entre la distancia y la velocidad, se deben realizar mediciones muy cuidadosas y precisas, de las distancias a las que se encuentran las galaxias que estás observando.
Pero antes de conocer el valor de la constante de proporcionalidad H, tienes que conocer algunas unidades para medir distancias ¿Qué unidades conoces para medir distancias?
El centímetro, el metro, el kilómetro y los años luz. En astronomía, las distancias a medir son tan enormes, que se ha inventado algunas unidades para longitudes muy, muy grandes; una de esas unidades es el año luz, que es la distancia que la luz recorre en un año y que es aproximadamente de diez billones de kilómetros.
Por ejemplo. cuando dicen que la Galaxia de Andrómeda se encuentra a dos punto cinco millones de años luz de nosotros, significa que la luz que ves de Andrómeda salió de ahí hace más de dos millones de años.
Y como la mayor parte de las galaxias del Universo se encuentran mucho más lejos que Andrómeda, se tiene la necesidad de inventar una nueva unidad de medida de longitud: el "parsec" que equivale a 3.26 años luz.
Y como las galaxias están aún más alejadas que algunos cientos de parsecs, se ha requerido incluir en las distancias entre galaxias múltiplos de parsec, como el "megaparsec", que equivale a un millón de parsecs; esto es 3.26 millones de años luz.
Continuando con la constante de Hubble, actualmente sabes que el valor de esta constante de proporcionalidad aproximadamente es de:
Ho = 70 km/Mpc/s
Lo que significa que, por cada millón de parsecs que las galaxias se alejan de nosotros, la velocidad a la que lo hacen es de 70 km por segundo.
¿Y si las galaxias se alejan, qué piensas que sucede con el tamaño del Universo?
Significa que el universo está creciendo.
Hubble, con ayuda de las ecuaciones lineales, concluyó que las galaxias se alejan unas de otras a una velocidad proporcional a su distancia, y que, por lo tanto, el universo está en expansión.
Piensa en el movimiento de los cuerpos. Un objeto en movimiento puede seguir una trayectoria recta o curva y puede desplazarse con velocidad constante o hacerlo con velocidad variable; en este caso, se dice que el objeto "se acelera".
El movimiento de un objeto acelerado puede representarse en gráficas de posición contra tiempo ¿Qué forma tienen este tipo de gráficas? ¿Qué nombre tienen?
¿Qué pasaría en una carrera de autos? ¿Ganó el auto que elegiste? ¿Te fijaste cuál de los dos autos iba ganando al principio? ¿Te parece si analizas qué fue lo que sucedió en esta carrera de autos?
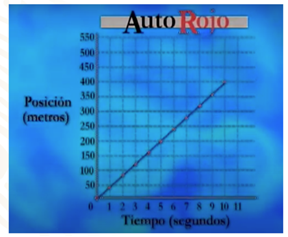
Unos instrumentos registraron las diferentes posiciones alcanzadas por el auto rojo cada 10 segundos del tiempo transcurrido. Los datos obtenidos se colocaron en la siguiente tabla:
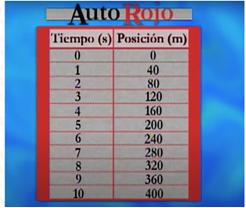
En la primera columna tienes los datos del tiempo en segundos, y en la segunda columna, la posición en metros.
Observa la gráfica correspondiente a estos datos.
Observa que los puntos graficados pertenecen a una recta. ¿A qué tipo de movimiento corresponde la gráfica obtenida? En efecto, la gráfica representa una relación lineal entre la posición y el tiempo. Esto significa que el auto rojo se desplazó con velocidad constante.
Observa ahora las posiciones y tiempos registrados para el auto azul.
¿Cómo es la gráfica que corresponde a estos datos?
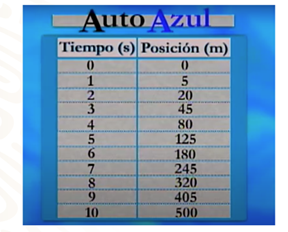
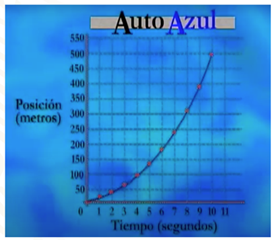
En este caso, los puntos graficados ya no pertenecen a una recta: la gráfica asociada a la relación entre la distancia recorrida y el tiempo transcurrido para el auto azul es evidentemente una curva llamada "parábola".
En general la gráfica asociada a la relación entre el tiempo y la distancia de un cuerpo con aceleración constante es una parábola.
¿Alguna vez has escuchado la frase: todo lo que sube tiene que bajar?
¿qué pensarías si supieras que esta frase y lo que ella implica, la puedes representar con una expresión cuadrática como las que has aprendido?
Observa cómo las matemáticas, y particularmente las ecuaciones cuadráticas, pueden ayudar, por ejemplo, para determinar la altura máxima que puede alcanzar un objeto al ser lanzado hacia arriba.
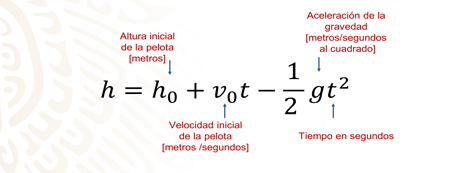
Si tuvieras que lanzar hacia arriba la pelota que tienes en la mano, su altura en el tiempo seguiría una ecuación cuadrática, dada por la siguiente expresión:
â„Ž = â„Ž0 + ð‘£0ð‘¡ − (1/2)ð‘”ð‘¡^2
En donde:
h0, es la altura inicial de la pelota en metros.
v0, es la velocidad inicial en metros por segundo.
g, es la aceleración de la gravedad en metros por segundo al cuadrado, y
t, es el tiempo.
¿Se parece esta ecuación a la ecuación cuadrática general? ¿Puedes reconocer el término cuadrático, el término lineal y el término independiente?
Revisa: aquí tienes la ecuación para determinar la altura de la pelota al ser lanzada hacia arriba:
â„Ž=â„Ž0+ð‘£0ð‘¡−(1/2) ð‘”ð‘¡^2 llámala "ecuación 1"y en seguida, la ecuación cuadrática general:
ax^2+bx+c=0
¿Cuál es el término cuadrático en la ecuación 1?
Es −(1/2) ð‘”ð‘¡^2.
¿Y los términos lineal e independiente?
El término lineal es vt y el término independiente es h0.
Observa cómo esta ecuación cuadrática puede ayudarte a resolver el siguiente ejercicio:
¿Cuál es la altura máxima que alcanzará la pelota cuando la lances hacia arriba desde tu altura? y ¿en qué momento alcanza esta altura máxima?
Para resolver este ejercicio, tienes que agregar algunos datos importantes, como:
Tu altura. Imagina que mides 1.70.
Ahora supón que lanzas la pelota a una velocidad de 20 metros por segundo. Y como te encuentras en el planeta Tierra, sabes, por tus clases de Física que la aceleración de la gravedad es de aproximadamente 10 metros por segundo al cuadrado.
Pero primero, reacomoda los términos de la ecuación uno, es decir,
A la ecuación â„Ž=â„Ž0+ð‘£0ð‘¡−(1/2) ð‘”ð‘¡^2
la puedes escribir, reordenando términos como:
â„Ž=−(1/2) ð‘”ð‘¡^2+ð‘£0 ð‘¡+â„Ž0

Así el coeficiente a=(-1/2)(10)= -5
El coeficiente b es el valor de la velocidad, es decir, 20; por lo que b=20.
Y, por último, el término independiente, cuyo valor es tu altura, en este ejemplo:
c = 1.70

Al sustituir los valores de estos coeficientes, tienes lo siguiente
â„Ž=−5ð‘¡^2+20ð‘¡+1.70
A esta ecuación la llamarás "Ecuación 2".

Ahora, para hallar la altura máxima que alcanza la pelota, y el tiempo en que lo hace, tienes que hallar el vértice de la parábola, lo cual puedes lograr aplicando la ecuación:
x = -b/2a, que llamarás "ecuación 3".
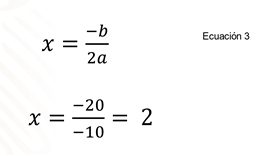
Sustituye los valores de los coeficientes en la ecuación tres:
x=-20/-10= 2
Observa que “x” es la “te” de tiempo en la ecuación, lo que sería en la Ecuación 1 el valor del tiempo “t”.
Ya obtuviste el valor de “x”, es decir, del tiempo “te”; ahora falta encontrar el valor de “y”, para lo cual sólo sustituyes en la ecuación dos el valor de “t”, que es igual a 2 segundos.
Entonces: h=-5(2)^2+20(2)+1.70
Al realizar las operaciones correspondientes, considerando la jerarquía de operaciones, tienes que:
h=-5(4)+40+1.70 = -20+40+1.70= 21.7 metros, que sería la altura máxima que la pelota alcanzaría a los dos segundos de ser lanzada.

¿Observaste el procedimiento y la importancia del uso de una ecuación cuadrática, en este ejemplo de lanzar una pelota hacia arriba para obtener la altura máxima que alcanzará y en qué momento?
Realiza la siguiente actividad:
Supón que lanzas la misma pelota, con la misma velocidad, pero en la superficie del planeta Marte, ¿alcanzaría la misma altura máxima que en el planeta Tierra? ¿Tú que piensas?
Debes aplicar la misma ecuación cuadrática que acabas de utilizar, pero la aceleración de gravedad no es la misma que en la Tierra, entonces lo único que tendría que modificar en la ecuación sería el valor de g, es decir, de la aceleración de gravedad para Marte.
La aceleración de la gravedad en el planeta Marte tiene aproximadamente el siguiente valor:
gm = 4 metros sobre segundo al cuadrado.

Por lo tanto, la ecuación cuadrática para el caso de lanzar una pelota verticalmente sobre la superficie de ese planeta, y obtener la altura máxima que alcanza es:
h=-(1/2)(4)t^2+20t+1.70 y realizando las operaciones indicadas h=-2t^2+20t+1.70
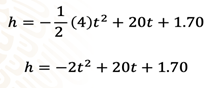
Resuelve la ecuación para obtener la solución a este problema astronómico. No olvides obtener primero el valor del tiempo utilizando la ecuación x=-b/2a.
Entonces, tienes que los valores de los coeficientes son:
A=-2; b=20 y c=1.70
Y, por lo tanto, x = -b/2a= -20/-4= 5
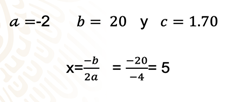
Ahora, sustituye este valor en la ecuación h=-2t^2+20t+1.70
que quedaría como, h=-2(5)^2+20t+1.70
Elevando al cuadrado el cinco, multiplicando por menos dos, y sumando, obtienes que:
h=-2(5)^2+20(5)+1.70=51.7
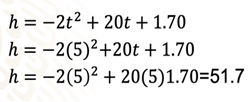
¿Qué sería la altura máxima alcanzada por la pelota y en el segundo 5?
Seguramente, entiendes cómo se utilizan las ecuaciones cuadráticas para resolver problemas concretos.
Hay más de 40,000 asteroides, y cientos de miles de cometas, y que se conoce muy bien la trayectoria de muchos de ellos. Incluso ya se ha enviado misiones no tripuladas a chocar con algún cometa.
Efectivamente, en el año 2005, la sonda espacial llamada Impacto profundo, se acercó al cometa Tempel 1, lanzándole un proyectil de unos 370 kg a una velocidad de 10 kilómetros por segundo, con una energía equivalente a 5 toneladas de TNT, que impactó la superficie del cometa, generándole un cráter de aproximadamente 150 metros de diámetro.
¿Y qué sucedió con los fragmentos que resultaron de la colisión?
Algunos fueron expulsados fuera del cometa, pero los más pequeños, alcanzaron una altura sobre la superficie del cometa de unos 300 metros, y luego cayeron de nuevo al cometa.
¿Y pueden los astrónomos calcular el tiempo en que todos esos pequeños fragmentos regresaron a la superficie?
Si y no sólo los astrónomos pueden calcular ese tiempo también tú puedes hacerlo, utilizando una ecuación cuadrática.
Calcula ese tiempo
Pero primero tienes que saber que la aceleración de gravedad del cometa Tempel 1 es de apenas 0.34 metros por segundo al cuadrado.

La ecuación cuadrática que resolverás es la siguiente: h=-(1/2) gt^2+h0
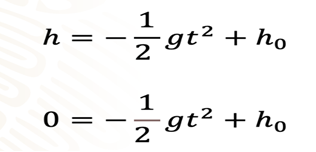
Es una ecuación cuadrática porque está elevada al cuadrado, aunque no tenga término lineal; entonces, el término cuadrático es -(1/2) gt^2, y el término independiente es h0.
Lo que quieres calcular es el tiempo que tardan los pequeños fragmentos cometarios en regresar a la superficie del cometa; es decir, cuando la altura es cero, después de que fueron lanzados a 300 metros de altura por la colisión.
Igualando a cero la altura sobre la superficie del cometa, tienes que: 0=-(1/2) gt^2+h0.
Sustituyes los valores de la aceleración de la gravedad y de la altura a la que fueron expulsados, y resuelve las operaciones:
0=-(1/2)(0.34)t^2+300
0=-0.17t^2+300
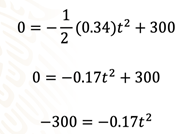
Restas 300 en ambos lados de la igualdad: -300=-0.17t^2.
Al dividir, ambos miembros de la ecuación entre -0.17 y realizar las operaciones:
-300/-0.17= (-0.17/-0.17)t^2
1764= 1t^2
1764=t^2
t^2=1764

Al sacar la raíz cuadrada, obtienes las dos raíces:
t es igual a la raíz cuadrada de 1764:
t1=42 y t2=-42.

Debido a que el resultado que buscas es el tiempo en que tardarán en caer los fragmentos a la superficie del cometa, elimina el resultado negativo y te quedas con la raíz positiva.
De tal manera, que, a los pequeños trozos lanzados por encima de la superficie del asteroide, les tomará 42 segundos en caer.
¿Te gustaron las ecuaciones lineales y las ecuaciones cuadráticas?
El reto de hoy:
Ahora que ya has visto las diferentes aplicaciones de las ecuaciones lineales y cuadráticas, te sugerimos buscar, en algún libro de física, la ecuación que relaciona el tiempo, la posición y la aceleración. Te darás cuenta de que es una relación cuadrática
Para resolver dudas, o ejercitar lo aprendido, te pueden apoyar en tu libro de texto; en caso de que no cuenten con él, lo puedes encontrar en Internet, en la página de la Comisión Nacional de Libros de Textos Gratuito.





Login to join the discussion