Relaciones de variación lineal

Relaciones de variación lineal

Aprendizaje esperado: consolidar contenidos del eje Número, álgebra y variación.

Énfasis: integrar los contenidos del tema Proporcionalidad.

¿Qué vamos a aprender?

El día de hoy retomarás el trabajo realizado a lo largo del ciclo escolar sobre relaciones de variación lineal, y compararás su representación algebraica, gráfica y tabular.

También analizarás las diferencias entre una variación de proporcionalidad directa con las de constante aditiva.

Para iniciar reflexiona las siguientes preguntas:

• ¿Qué características debe tener la relación entre dos variables para ser una relación de proporcionalidad directa?
• ¿Cómo puedes identificar si la relación entre dos variables representa una relación con variación lineal?
• ¿Cómo son las gráficas de este tipo de relaciones?

¿Qué hacemos?

Durante esta sesión se dará respuesta a estas preguntas y analizarás diversas situaciones-problema, para cada tipo de relación.

Una relación de proporcionalidad directa es una relación entre dos variables, de manera que, ambas aumentan o disminuyen en la misma proporción, es decir, si una aumenta al doble, la otra también aumenta al doble.

La expresión general de una relación de proporcionalidad directa, es de la forma: y = kx, donde “y” representa a la variable dependiente, “x”, a la variable independiente, es decir, los valores de “y” dependen de los valores que tome “x” y “k”, representa a la constante de proporcionalidad.

Por ejemplo, la tabla muestra una relación de proporcionalidad directa, entre los días de hospedaje en cierto hotel y el costo.

En este caso, los días de hospedaje representan a la variable independiente, “x”, como el costo del hospedaje depende de los días, entonces representa a la variable dependiente “y”, y la constante de proporcionalidad es el costo por día de alojamiento, que es igual a 450.

Con esta información ya puedes establecer la expresión algebraica que representa la situación, y es y = 450x. Esto quiere decir, que para saber el costo, según los días de hospedaje, basta con multiplicar 450 por los días correspondientes.

Ya debes recordar claramente lo que son las relaciones de proporcionalidad directa.

Es momento de responder la segunda pregunta:

¿Cómo puedes identificar si la relación entre dos variables representa una relación con variación lineal?

Una relación de variación lineal es la relación entre dos variables “x” y “y”. En ellas, la variable dependiente aumenta de manera constante.

En estas relaciones se involucran dos valores que son constantes, uno es multiplicativo y la otro, es aditivo.

La expresión general de una relación de variación lineal, es de la forma: y = kx + b, donde “y” representa a la variable dependiente, “x”, a la variable independiente, “k”, representa a la constante multiplicativa y “b” a la constante aditiva.

Por ejemplo, la tabla muestra una relación de variación lineal, a diferencia del caso anterior, en esta situación, el hotel cobra una comisión por la reservación, que está representada por la constante aditiva, por eso no se cumple con una relación de proporcionalidad directa.

En estos casos, para obtener la constante aditiva, se calcula la diferencia entre valores consecutivos de “ye”, por ejemplo, 1 200 – 750 = 450. Y para la constante aditiva, se le resta al costo por un día, la constante multiplicativa, es decir, 750 – 450 = 300.

Con esto ya puedes obtener la expresión algebraica de la situación que es: y = 450x + 300.

Ya se respondieron dos de las tres preguntas planteadas, pasa a la última, que dice:

¿Cómo son las gráficas de este tipo de relaciones?

Hablando de las relaciones de proporcionalidad directa y las de variación lineal.

¿Qué es la razón de cambio y cómo se obtiene? Y ¿Qué es la pendiente de una gráfica?

Empieza analizando las características de las gráficas de los casos vistos.

Las gráficas de las relaciones de proporcionalidad directa y de variación lineal son líneas rectas.

En el caso de las gráficas de proporcionalidad directa, de la forma y = kx, las rectas pasan por el origen. En la imagen puedes ver la gráfica de la relación días de hospedaje y costo, que viste antes y está dada por la expresión algebraica y = 450x.

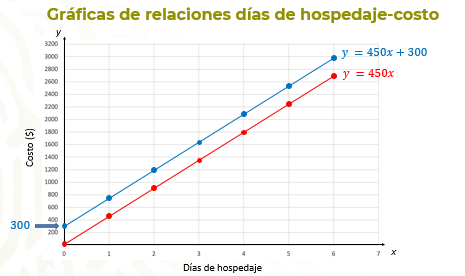
En el caso de relaciones de la forma y = kx + b, el punto donde la recta interseca al eje “y•”, está dado por el valor de “b”. En el caso que viste antes, la expresión algebraica es y = 450x + 300, por lo que la recta corta al eje “y” en la coordenada (0, 300).

Ya has respondido a las tres preguntas que se hicieron al inicio de la sesión, ahora responde a las otras preguntas.

¿Qué es la razón de cambio y cómo se obtiene?

En relaciones de la forma y = kx + b, la razón de cambio es la variación de una magnitud respecto a la otra.

Analiza el siguiente caso.

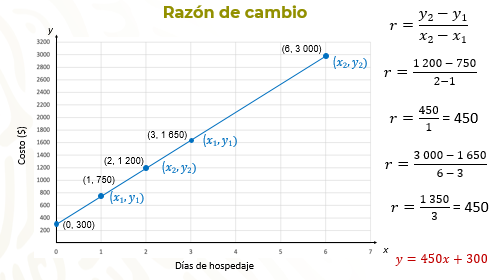
En la gráfica que observas, sobre la recta que representa a la relación lineal, tienes varios puntos señalados. Para encontrar la razón de cambio se identifican dos parejas de coordenadas, que llamaremos: (x1, y1) y (x2, y2) y entonces la razón, “r” es igual a y2 menos y1 entre x2 menos x1.

Identifica los valores de “x” y de “y”, los sustituyes en la expresión anterior y operas: r es igual a 1 200 menos 750 sobre 2 menos 1, al resolver las operaciones tenemos que r = 450 entre 1, igual a 450, que representa la razón de cambio en este caso.

Pero puedes utilizar cualquier pareja de coordenadas, por ejemplo, (3, 1650) y (6, 300), en este caso, “r” es igual a 3 000 menos 1 650 sobre 6 menos 3, de donde, “r” es igual a 1 350 entre igual a 450.

En este caso la razón de cambio, 450 representa el costo por día de hospedaje, con esto puedes establecer la expresión algebraica de la forma y = kx + b, que representa la situación: en este caso, y = 450x + 300, ya que 300 es el punto donde la recta interseca al eje “y”, Y como pueden notar es la misma expresión que viste antes.

Ya solo falta responder la última pregunta, ¿Qué es la pendiente?

Se denomina pendiente a la inclinación de una recta respecto al eje “x”. En una relación lineal, la pendiente es igual a la razón de cambio. A mayor pendiente, mayor razón de cambio.

Has hecho una minuciosa recapitulación sobre las relaciones de proporcionalidad directa y las de variación lineal.

Ahora, resuelve una situación problema donde aplicarás los conceptos vistos.

Dos automóviles iniciaron un viaje en carretera a la misma hora, en el mismo punto y en la misma dirección. Las siguientes tablas muestran su comportamiento de cada uno durante el viaje.

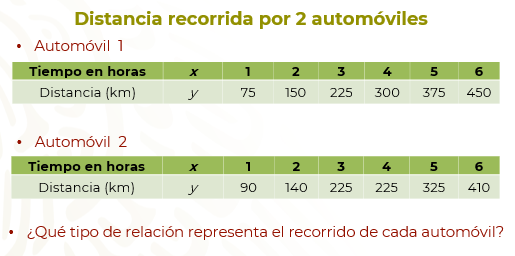
Analiza las tablas.

¿Qué tipo de relación representa el recorrido de cada automóvil?

Para responder la pregunta que se plantea, analiza las gráficas que representan cada situación.

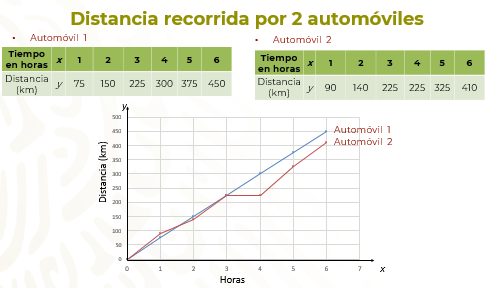
Como puedes observar en el caso del automóvil 1 la gráfica permite ver que las horas y la distancia recorrida representan una relación de proporcionalidad directa, ya que es una línea recta que pasa por el origen, en el caso del automóvil 2, al no ser una línea recta, no representa una relación lineal, lo que significa que el recorrido del automóvil no fue constante.

Ahora, enfoca el análisis en la situación del automóvil 1, que es el que representa una relación de proporcionalidad directa.

¿Cuál es la razón de cambio en este caso? ¿Qué expresión algebraica representa la situación?

Para establecer la razón de cambio, identifica dos parejas de coordenadas (x, y) y las nombras (x1, y1) y (x2, y2), en este caso elegirás (2, 150) y (3, 225). Ahora resuelve “r” igual a y2 menos y1 sobre x2 menos x1, al sustituir la expresión por los valores correspondientes, tienes que “r” es igual a 225 menos 150 sobre 3 menos 2, al resolver las operaciones tienes que “r es igual a 75 entre 1, igual a 75. Por lo que la razón de cambio es igual a 75.

Ahora, para obtener la expresión algebraica, identifica el valor unitario, que en este caso es 75, que también representa la constante de proporcionalidad, por lo que la expresión algebraica correspondiente queda como: y = 75x.

Como puedes ver, en una relación de proporcionalidad directa, la razón de cambio es igual a la constante de proporcionalidad.

En la situación anterior, a partir de la información de una tabla de datos, pudiste construir una gráfica para identificar que se trataba de una relación de proporcionalidad directa y, a partir de ésta, obtuviste la razón de cambio y la expresión algebraica correspondiente al problema.

Ahora, observa una nueva situación-problema.

Un grupo de amigos saldrá de vacaciones y quieren rentar un automóvil por 5 días, para poder facilitar sus traslados.

La casa arrendadora de automóviles les ofreció dos opciones:

Opción 1: El automóvil tiene un costo de $520 por día.

Opción 2: El automóvil tiene un costo diario de $400 más un pago inicial de $420.

¿Cuánto tienen que pagar por los 5 días, en cada caso?

¿Qué opción les conviene más?

¿Qué tienes que hacer para responder las preguntas anteriores?

¿Qué tipo de relación se establece entre los datos del problema?

Para analizar que situación les convenía más, los amigos registraron en una tabla el costo de la renta, en cada caso, hasta seis días, por si decidían rentar un día más el vehículo.

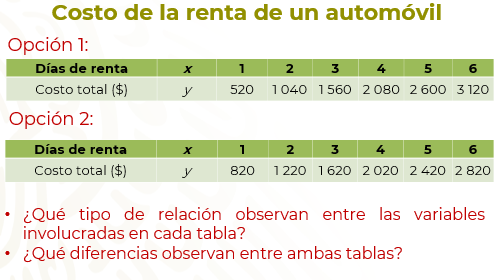
Registra en tu cuaderno las diferencias que identificaste en la relación que se establece entre la cantidad de días de renta y el costo.

Observa si coinciden sus razonamientos con la siguiente explicación. Grafica los valores de ambas tablas en el mismo plano.

Para construir las gráficas, ubica las parejas de puntos (x, y), de cada relación, sobre el plano cartesiano y trazamos una recta para unirlos. Primero lo haces para la opción 1, y posteriormente, para la opción 2.

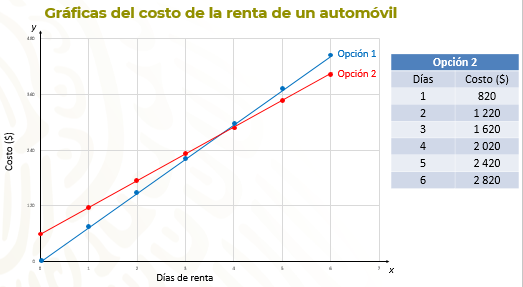
En las gráficas puedes ver que ambas situaciones representan relaciones de variación lineal, ya que son rectas y que la opción 1, es una relación de proporcionalidad directa porque pasa por el origen.

También comprueba que el costo por 5 días de renta es menor en la opción 2.

Pero ¿cuál es la razón de cambio en cada caso?

¿Qué expresión algebraica representa cada situación?

Para la opción 1, se eligieron dos parejas de coordenadas: (1, 520) y (2, 1 040) y se obtiene que la razón de cambio es r = 1 040 menos 520 sobre 2 menos 1, igual a 520 entre 1, igual a 520. En este caso, por ser una relación de proporcionalidad directa, bastaría con restar valores consecutivos de “y” para establecer la razón de cambio.

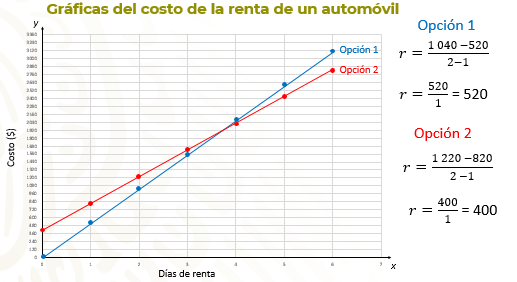
Ahora observa la opción 2, elige las parejas de coordenadas (1, 820) y (2, 1 220) y resuelve las operaciones: “r” = 1 220 menos 820 sobre 2 menos 1, que es igual a 400 entre 1, igual a 400.

Ya tienes la razón de cambio en ambos casos, en el caso de la opción 2 la razón de cambio es menor, lo que significa la que opción 1 tiene mayor pendiente, como puedes observar en la inclinación de las rectas.

Usa la información obtenida para establecer la expresión algebraica en cada caso.

¿Ya tienes lista la expresión algebraica que representa cada situación?

Observa lo siguiente para validar sus respuestas.

Cómo pudiste ver, la opción 1 representa una relación de proporcionalidad directa cuya expresión general ya conocen: y = kx,

En estos casos, como se mencionó antes, la razón de cambio es igual a la constante de proporcionalidad, entonces la constante de proporcionalidad es 520, por lo tanto, la expresión algebraica es y = 520x.

El caso de la opción 2, representa una relación lineal de la forma y = kx + b.

En estos casos, la razón de cambio es igual a la constante multiplicativa, que en esta relación es 400, para obtener la constante aditiva, le restamos al valor de “y”, cuando “x” es uno, la constante multiplicativa, es decir, 820 menos 400 igual a 420.

Y con esta información podemos establecer la expresión algebraica que es y = 400x + 420.

En los casos anteriores, pudiste comparar dos relaciones de variación lineal, una de ellas de proporcionalidad directa.

Reflexiona lo siguiente: ¿Una relación de proporcionalidad directa representa una relación de la forma y = kx + b? Busca argumentos para justificar su postura.

Más adelante se dará respuesta a la pregunta para que puedan validar su postura. Por ahora, analicemos la siguiente situación problema presentada en una gráfica para obtener la razón de cambio y la expresión algebraica correspondiente.

Tres amigos juegan en línea un videojuego en el que acumulan cierta cantidad de puntos, al superar cada etapa, de acuerdo con el nivel de dificultad en el que juegan.

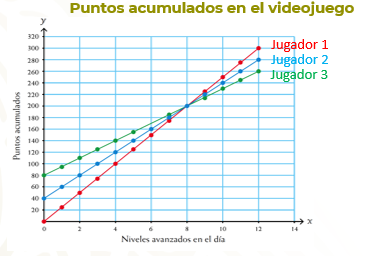
Las siguientes rectas representan los puntos acumulados por cada uno el día de hoy.

Dos jugadores continuaron una partida que guardaron el día anterior y el otro inició un nuevo juego.

Analiza las rectas y respondan:

¿De jugador inicio el juego el día de hoy?

¿Cuál es la razón de cambio en cada caso?

¿Qué gráfica tiene mayor pendiente?

¿Qué expresión algebraica representa a cada recta?

Observa nuevamente las gráficas para responder las preguntas.

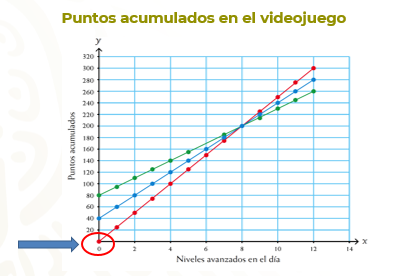
Para la primera pregunta sobre qué jugador inicio el juego el día de hoy, la recta roja inicia en el origen, lo que significa que el jugador no tenía puntos acumulados, por lo que ese jugador 1 inicio el juego el día de hoy.

Ahora, calcula la razón de cambio en cada caso, para responder a la segunda pregunta.

Primero elige dos pares de coordenadas en cada caso. Busca puntos que puedas establecer con exactitud valores de “y”, por ello, para cada caso, elegirás las coordenadas en las que los valores de “x” son 8 y 12.

Empieza con el jugador 1. Las coordenadas son: (8, 200) y (12, 300), por lo tanto, “r” es igual a 300 menos 200 sobre 12 menos 8, al resolver las operaciones, tienes que la razón de cambio es igual a 100 entre 4, igual a 25.

Para el jugador 2, tenemos las coordenadas: (8, 200) y (12, 280), al realizar los cálculos correspondientes tenemos que la razón de cambio es igual a 80 entre 4 igual a 20.

Y para el caso del tercer jugador las coordenadas elegidas son: (8, 200) y (12, 260), en este caso, la razón de cambio es igual a 60 entre 4, igual a 15.

Con esto puedes concluir que la gráfica del jugador 1 tiene mayor razón de cambio, lo que significa que tiene mayor pendiente, como pueden observar.

Establece la expresión algebraica que representa la situación.

Empieza con el jugador 1.

Como viste antes, la recta representa una relación de proporcionalidad directa, por lo tanto, la razón de cambio, 25, es igual a la constante de proporcionalidad, por lo que la expresión algebraica correspondiente es: y = 25x.

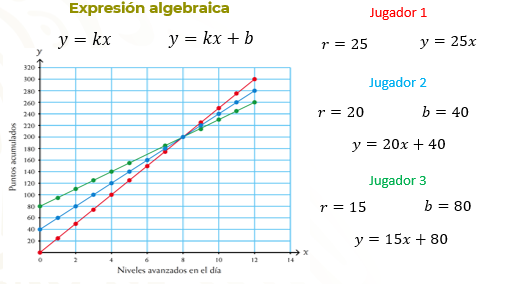
Para el caso del jugador 2, sabemos que la razón de cambio es 20 y que la ordenada al origen es 40, es decir, b es igual a 40. Entonces, la expresión algebraica de la recta azul es y = 20x + 40.

Por último, el caso de la recta del jugador 3, la razón de cambio es igual a 15 y “b” es igual a 80, por lo tanto, la expresión algebraica correspondiente es: y = 15x + 80.

El reto de hoy:

Observa un breve resumen sobre el tema visto en la sesión.

Relación de variación lineal es de la forma: y = kx + b

Las relaciones de proporcionalidad directa son de la forma: y = kx

La gráfica de este tipo de relaciones es una línea recta.

En relaciones de la forma y = kx + b, “b” determina la ordenada al origen.

En las relaciones de proporcionalidad directa, la recta pasa por el origen.

En una relación del tipo y = kx + b, cuando b es igual a cero, la relación es de proporcionalidad directa.

Durante la lección analizaste las diferencias entre una relación de proporcionalidad directa y una relación de variación lineal, analizaste y representaste tabular, algebraica y gráficamente relaciones lineales, este tipo de relaciones.

No olvides revisar lo aprendido en esta clase en tu libro de texto de Matemáticas 1. Ahí encontrarás otras actividades muy interesantes para practicar lo que aprendiste o para aclarar las dudas que tengas.

¡Buen trabajo!

Gracias por tu esfuerzo.

Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html