Reglas de la suma y del producto
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:23
Reglas de la suma y del producto
Aprendizaje esperado: resuelve problemas que implican calcular la probabilidad de eventos complementarios, mutuamente excluyentes e independientes.
Énfasis: resolver problemas que impliquen el uso de las reglas de la suma y del producto.
¿Qué vamos a aprender?
Considera que la probabilidad calcula qué tan posible es que ocurra una situación que no es segura.
Existen situaciones o eventos que generan cierta incertidumbre, pues muestran inseguridad en su posibilidad de ocurrencia. Determinar qué tan posible es que ocurra un evento incierto es la tarea de la probabilidad.
¿Se podría decir que la probabilidad le pone número a una corazonada?
Una corazonada es la sensación de que algo va a ocurrir. Y esta sensación puede verse influenciada por suposiciones de distinta naturaleza u origen.
Sin embargo, la probabilidad reúne e interpreta información para poder hacer predicciones. Lo que reduce el riesgo y la desventaja en la toma de decisiones.
Igual que otras áreas de las Matemáticas, el campo de estudio de la probabilidad resulta ser muy extenso.
Por ello, delimita el ámbito de influencia del trabajo de esta sesión.
El propósito se expresa de la siguiente manera: “resolver problemas que impliquen el uso de las reglas de la suma y del producto”.
Necesitarás tu cuaderno de notas y un lápiz. Si cuentan con una calculadora será de mucha ayuda.
Además, registra tus dudas e inquietudes. Realiza las anotaciones que consideres necesarias respecto a esta sesión.
¿Qué hacemos?
Todos los días suelen presentarse situaciones en las que debes estimar qué tan posible es que algo suceda.
Ganar una rifa o un sorteo, predecir quién ganará en una competencia de automovilismo, suponer al ganador de un partido de futbol, anticipar qué tan posible es que llueva un día en particular, son algunos ejemplos.
En todas estas situaciones existe algún grado de incertidumbre. Un matemático dijo al respecto: “Es irracional pensar que lo más probable sea cierto, pero no es en modo alguno irrazonable actuar conforme a lo más probable”.
La probabilidad ofrece recursos para la estimación de posibilidades de ocurrencia. Te permite identificar con mayor claridad las condiciones que rodean una situación para tomar mejores determinaciones.
Observa el siguiente video del inicio al minuto 01:41.
- ¿Qué es el azar? ¿Qué es aleatorio?
https://www.youtube.com/watch?v=ViMZbNG5Klw&feature=youtu.be
Por eso, preguntarse si el mes de enero tendrá 31 días no es una situación aleatoria o que dependa de la suerte. Es un “evento seguro”.
Que el día de mañana el Sol salga por el poniente es un “evento imposible”. No ocurrirá. Por otro lado, saber exactamente cuántas personas abordarán un vagón del metro en la siguiente estación es incierto, depende del azar.
Efectivamente, un evento aleatorio o de azar puede tener distintos resultados. Calcular qué tan posible es que ocurra es tarea de la probabilidad.
Analiza la siguiente información.
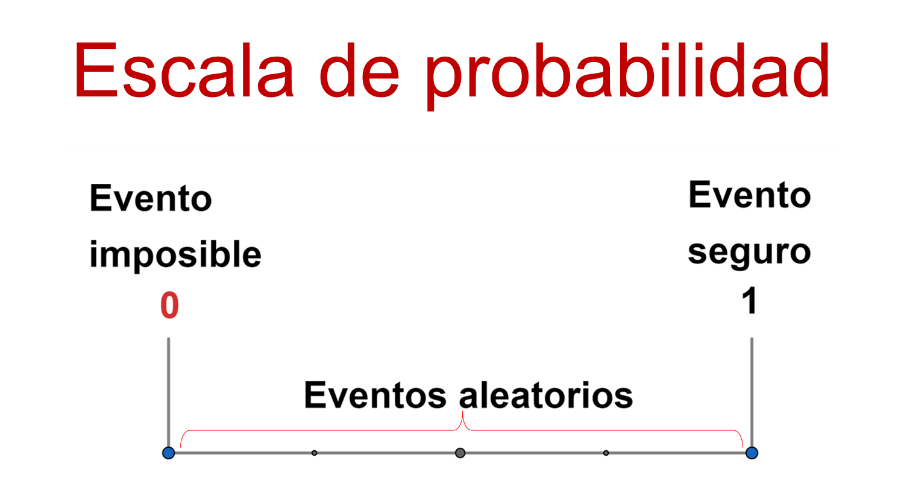
Para representar probabilidades se usa una escala numérica entre 0 y 1. Esto quiere decir que, la medida de la probabilidad de cualquier evento se encuentra en ese intervalo, incluyendo el 0 y el 1. Y se puede expresar en forma de número decimal, fracción o porcentaje.
Si la probabilidad es 0, significa que esa situación no ocurrirá, es decir, es un “evento imposible”. En cambio, si la medida es 1, la situación seguro que ocurrirá, es decir, es un “evento seguro”.
Para calcular la posibilidad de ocurrencia de un evento aleatorio se utiliza la siguiente fórmula. Indica que para obtener la probabilidad del “evento A” se divide el número de casos favorables entre el total de los casos posibles.

Supón que vas a comer a un restaurante, al terminar de comer están sirviendo el postre, de modo que indistintamente te pueden servir helado de sabor fresa, vainilla o chocolate.
Al calcular la probabilidad de que te sirvan helado de fresa, se utiliza la fórmula:
Número de casos favorables: uno.
Entre el total de casos posibles: tres.
La probabilidad de que te sirvan helado sabor a fresa es de un tercio, o cero punto treinta y tres o treinta y tres por ciento.
En términos matemáticos, la probabilidad de que te sirvan fresa es un tercio.
Que también se puede expresar como cantidad decimal o porcentaje.
Si se toma en cuenta que no se desea el sabor vainilla. En términos matemáticos, eso cambia el cálculo que hiciste de la probabilidad. Para esta nueva condición, tu preferencia es que te sirvan helado sabor fresa o sabor chocolate. Cualquiera de los dos, pero no de vainilla.
Eso se representa y se calcula mediante la regla de la suma.
La regla de la suma indica que cuando dos eventos que son parte de un mismo espacio muestral y que además son mutuamente excluyentes, la probabilidad de que ocurra uno u otro se puede determinar al sumar las probabilidades de ambos.

En la situación que analizaste, los eventos ¿son mutuamente excluyentes?
Si te sirven helado sabor a fresa no te sirven sabor a chocolate ni vainilla. Te sirven helado de un solo sabor.
Utilizando la regla de la suma se tiene que:
La probabilidad de que te sirvan helado sabor a fresa es un tercio. Y la probabilidad de que te sirvan helado sabor chocolate es de un tercio más. Da como resultado dos tercios o 66 por ciento, aproximadamente.
La probabilidad de que te sirvan helado sabor a fresa o chocolate es de 0.66.
Sabiendo que la escala de probabilidad va de cero a uno, 0.66 representa una gran probabilidad de que te sirvan helado de fresa o de chocolate.
Analiza la siguiente situación que te permite valorar de nueva cuenta las propiedades descritas.

Al término del entrenamiento de los 11 jugadores titulares del equipo local de futbol soccer, el encargado de la utilería nota que uno de ellos olvidó sus espinilleras.
Tomaron parte en el entrenamiento el portero, cuatro defensas, cuatro mediocampistas y dos delanteros.
¿Cuál es la probabilidad de que las espinilleras pertenezcan al portero -sea éste el evento A- o que pertenezca a un defensa, sea éste el evento B?
Puesto que cada jugador tiene asignada su función dentro del equipo, los eventos son mutuamente excluyentes.
Se debe utilizar la regla de la suma.
Examinemos la solución.
La probabilidad de que las rodilleras pertenezcan al portero, es decir, la probabilidad del evento A es de un onceavo.
La probabilidad de que las rodilleras pertenezcan a un defensa, es decir, la probabilidad del evento B es de cuatro onceavos.
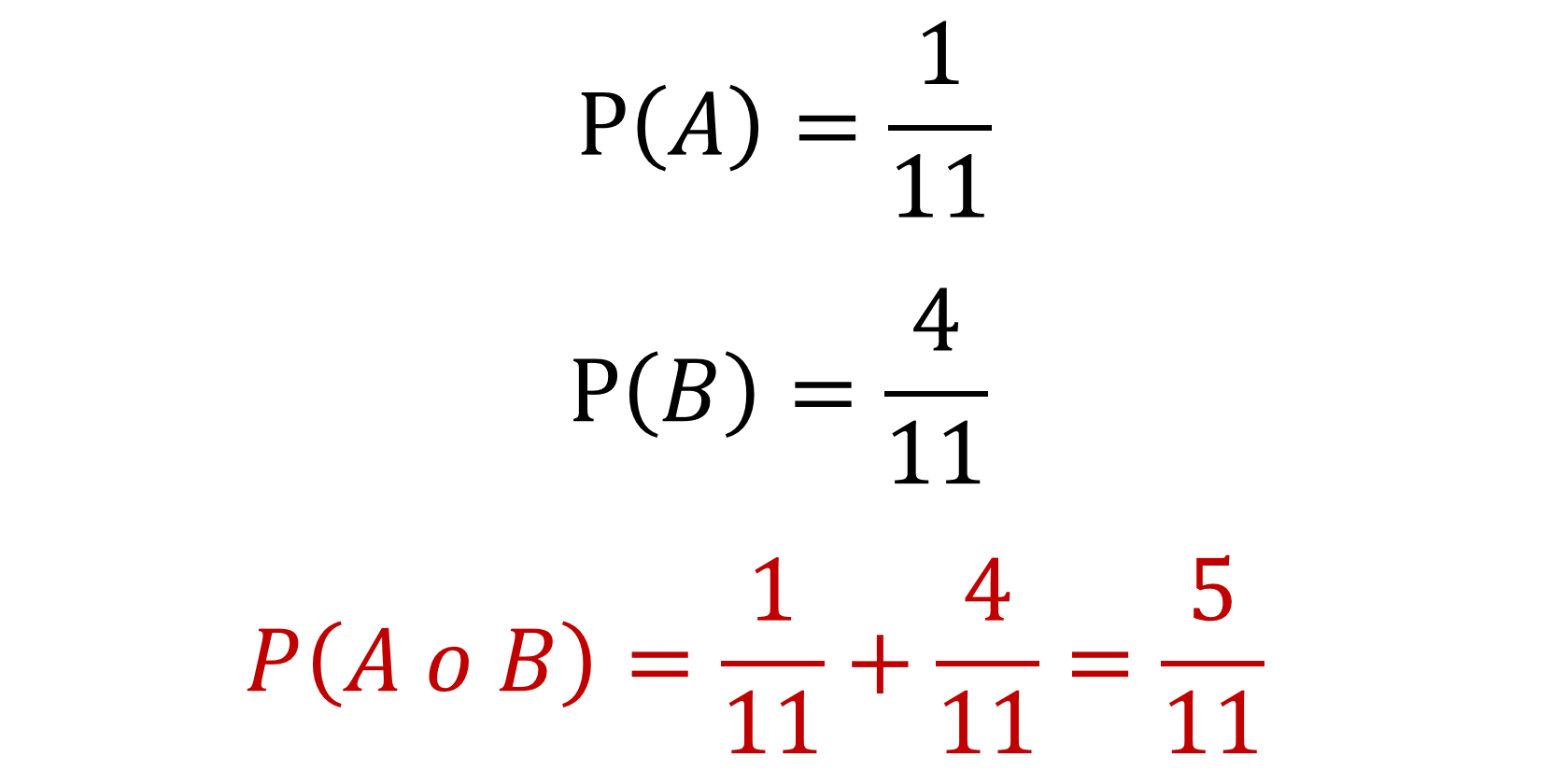
Ya que se necesita saber la probabilidad de que las espinilleras pertenezcan al portero o a un defensa, las probabilidades deben sumarse.
Un onceavo más cuatro onceavos son cinco onceavos. Aproximadamente igual a 0.45.
Así, la probabilidad de que las espinilleras olvidadas pertenezcan al portero o a un defensa es de aproximadamente 45 por ciento.
Se puede notar que, cuando aplicas la regla de la suma, aumenta la probabilidad de ocurrencia de un evento.
En lo referente a probabilidad se deben conocer las características y condiciones que representa cada evento aleatorio para interpretarlo correctamente.
Analiza otro ejercicio.
Mariana y Raúl juegan lanzando un dado de 6 caras y una moneda.
Para su próximo turno se pusieron las siguientes condiciones:
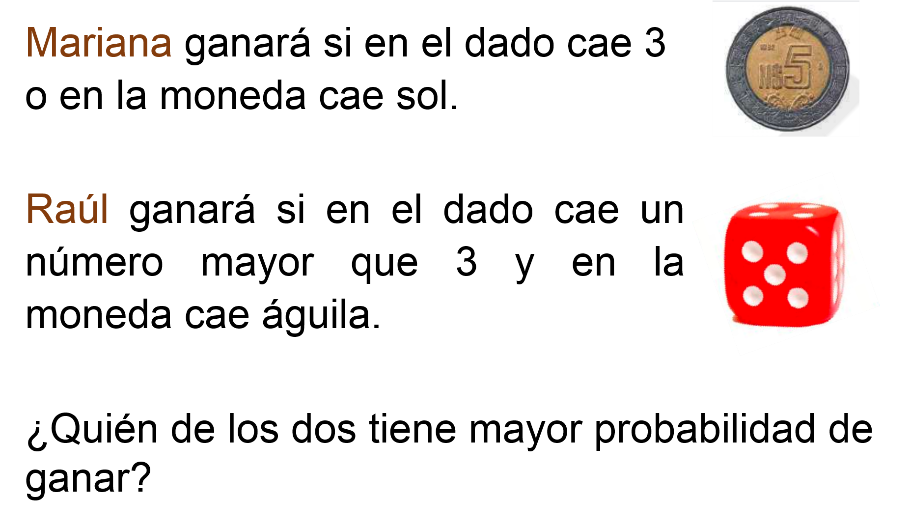
Si se consideran las propiedades que se han descrito durante esta sesión, se realizarán los cálculos correspondientes para saber quién tiene mayor probabilidad de ganar y si la competencia es justa.
En el caso de Mariana se denomina “evento A”, obtener el número “3” al lanzar el dado. Y se considera el “evento B” al evento que cumple con la condición de que caiga “sol” al lanzar la moneda.

Puesto que Mariana gana si cae tres en el dado o sol en la moneda, se utiliza la regla de la suma.
Probabilidad de “A” o “B” es igual a la probabilidad del “evento A”, un sexto, más la probabilidad del “evento B”, un medio. El resultado es dos tercios, que es aproximadamente igual a 0.66 o 66 por ciento.
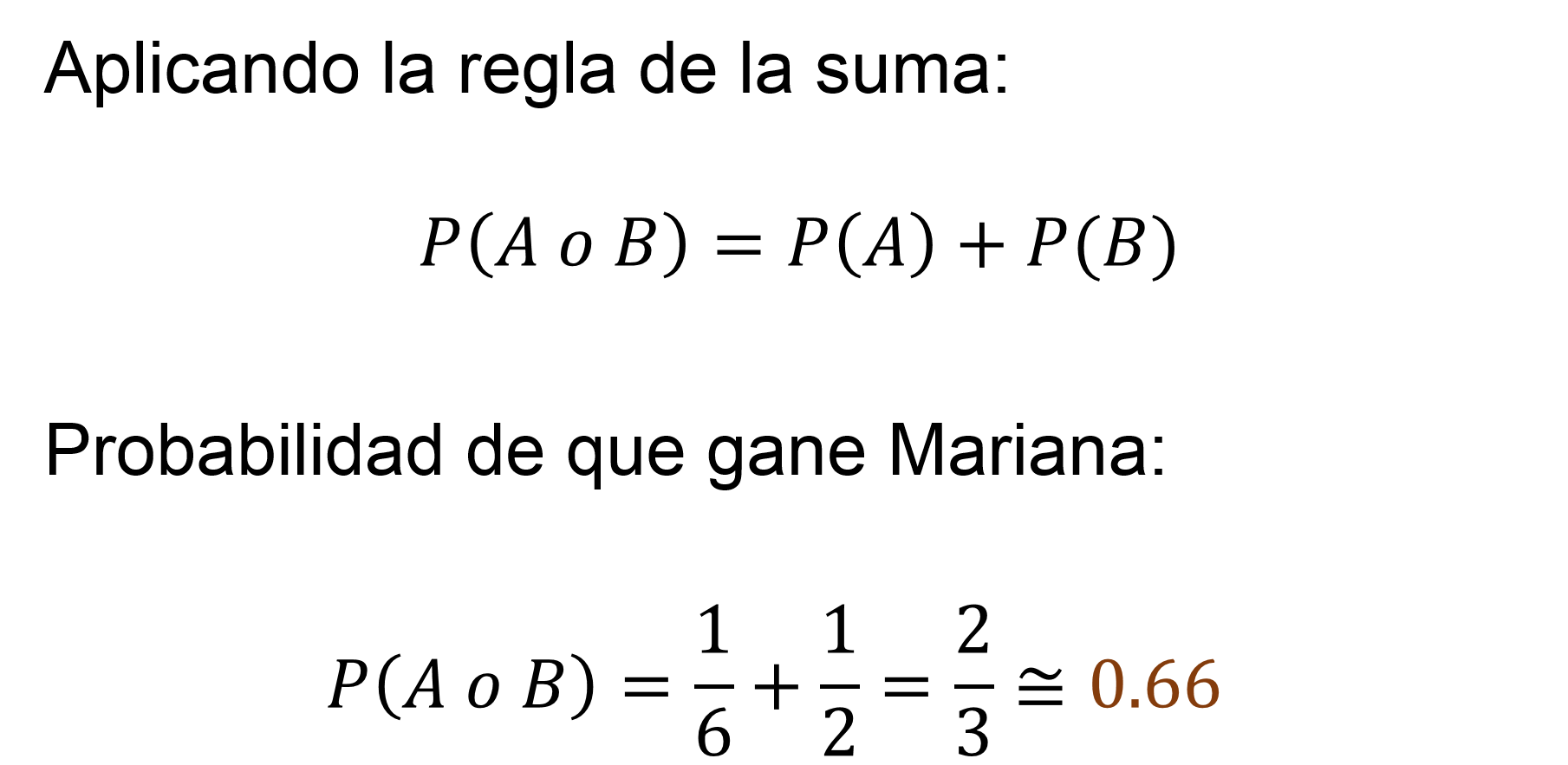
Considerando las condiciones para que gane Raúl, se denomina “evento C” al evento de que el dado caiga en un número mayor que tres. Esto sucede al obtener el cuatro, el cinco y el seis. Tres casos favorables de seis casos posibles. La probabilidad es de un medio, 0.5 o del 50 por ciento.

Y se denomina “evento D” al que indica que caiga “águila” en la moneda.

La probabilidad de “D” es igual a uno entre dos, es decir, un medio, 0.5 o 50 por ciento.
Cuando se suman las probabilidades de los eventos “C” y “D” se obtiene un entero. ¿Significa que se tiene un evento seguro? No necesariamente.
Recuerda que la regla de la suma se utiliza cuando la situación pide que se cumpla una u otra condición.
Para que gane Raúl debe caer un número mayor que tres en el dado y también caer águila al lanzar la moneda. Debe cumplir ambas condiciones a la vez.
En este caso se debe utilizar otro recurso, denominado “la regla del producto”. Que se describe a continuación.
La regla del producto determina que, en el cálculo de probabilidades, sean A y B dos eventos independientes, la probabilidad de que ocurran A y B es igual al producto de las probabilidades de los eventos A y B.

Pero cuando multiplicas dos cantidades, el resultado es mayor que cada una de éstas, pero eso no ocurre en todos los casos. Si se utiliza la regla del producto en la situación de Raúl se observará esta condición.
Se encuentra que la probabilidad del “evento C”, de obtener un número mayor que tres en el dado es un medio.
Y la probabilidad del “evento D”, que caiga “águila” al lanzar la moneda, es un medio.
Para que ocurran C y D tienes:
Probabilidad de C y D es igual a la probabilidad de C por D. Es decir, un medio por un medio.
La probabilidad de que gane Raúl es de un cuarto o 0.25.

Se tiene que la probabilidad de que gane Mariana es de 66 por ciento. Ahora se sabe que la probabilidad de que gane Raúl es de 25 por ciento.
Por lo que Mariana tiene mayor probabilidad de ganar este turno.
En un principio pudo suponerse que la condición era ventajosa para Raúl. Sin embargo, resultó que él tiene menor probabilidad de ganar. La probabilidad favorece a Mariana.
La diferencia se debe en el caso de Mariana, que se debe cumplir con una u otra condición, por eso se suman las probabilidades.
Para que Raúl resulte ganador, se debe cumplir con una y con otra condición.
Se puede notar que la diferencia en las condiciones es la conjunción. Cuando la conjunción es “o”, las probabilidades se suman. Cuando la conjunción es “y”, las probabilidades se multiplican.
Entonces, si en un experimento de azar debe ocurrir uno u otro evento, las probabilidades de que estos ocurran se suman.
Y si deben ocurrir ambos eventos, entonces las probabilidades se multiplican.
El que pueda ocurrir uno u otro evento aumenta la posibilidad de ocurrencia. Mientras que el que ocurra uno y otro evento a la vez, la disminuye.
Al utilizar la regla del producto, la probabilidad obtenida siempre es menor que la probabilidad de que ocurra cualquiera de los dos eventos considerados.
Analiza el siguiente ejercicio para identificar la diferencia entre estas reglas de la probabilidad.
El grupo 3°D de la “Escuela secundaria Río Verde” consta de 45 alumnos y alumnas: 9 de ellos tienen 14 años, mientras los demás tienen 15 años. En el grupo, 30 alumnos portan el uniforme completo y 15 lo llevan incompleto. El director de la escuela mandó al prefecto para que elija al azar a uno de los alumnos del grupo y le aplique una encuesta.

¿Cuál es la probabilidad de que el alumno seleccionado tenga 14 años o lleve el uniforme completo?
¿Cuál es la probabilidad de que el alumno tenga 15 años y porte el uniforme incompleto?
Los eventos que se describen son independientes. Portar el uniforme completo o incompleto no depende de si un alumno o alumna tiene 14 o 15 años. Se pueden utilizar las fórmulas de la suma y del producto que se han mencionado.
Para resolver se debe tomar en cuenta que el total de alumnos del grupo es de 45, se hacen los cálculos.
Analizando la primera situación, se denomina “evento A”, que el alumno elegido por el prefecto tenga 14 años. Se designa “evento B”, que el alumno elegido lleve el uniforme completo.

La probabilidad del “evento A”, que el alumno tenga 14 años, es 9 entre 45. Que es equivalente a un quinto.
La probabilidad del “evento B”, que lleve el uniforme completo, es 30 entre 45. Lo que es equivalente a dos tercios.
En este caso se debe cumplir con una condición o con la otra, por lo que se utiliza la regla de la suma.
Probabilidad de A o B es igual a la probabilidad de A más la probabilidad de B.
Se tiene que la probabilidad de A o B es igual a un quinto más dos tercios. Que es igual a trece quinceavos. Aproximadamente 86 por ciento.

Notas que el porcentaje de ocurrencia es significativamente más alto debido a que ocurre uno u otro evento. Se explica por la suma de las probabilidades.
Falta por determinar lo que sucede para las otras condiciones.
Para la segunda pregunta del ejercicio, se denomina “evento C” aquel en que la edad del alumno elegido sea 15 años. Y denota “evento D” que el alumno elegido lleve el uniforme incompleto.

La probabilidad del “evento C”, que el alumno tenga 15 años, es 36 entre 45. Que es equivalente a cuatro quintos.
La probabilidad del “evento D”, que porte el uniforme incompleto, es 15 entre 45. Lo que es equivalente a un tercio.
En esta situación se debe cumplir con ambas condiciones, la regla que se debe utilizar es la del producto.
Probabilidad de C y D es igual a la probabilidad de C por la probabilidad de D, que es igual a cuatro quintos por un tercio y es igual a cuatro quinceavos. Aproximadamente 26 por ciento.

Y se puede advertir que disminuye la posibilidad de ocurrencia al tener que cumplir ambas condiciones.
Las propiedades de la probabilidad se utilizan como herramientas profesionales en numerosas actividades, como las bolsas de valores, la selección de contenidos digitales, el desarrollo de videojuegos, las estrategias de promoción de marcas y en la evaluación de riesgos médicos, entre otros.
Un ejemplo de la utilidad de la probabilidad es cuando se adquiere una computadora, un refrigerador o un teléfono móvil. Todos esos artículos tienen una vida promedio calculada con base en la probabilidad. A partir de ese cálculo los fabricantes extienden su tiempo de garantía.
Lo mismo si se trata de un refrigerador que de un automóvil, la probabilidad de que ocurra un desperfecto aumenta notablemente cuando vence el periodo de garantía.
Durante tu trayecto formativo seguirás trabajando con temas relacionados con la probabilidad. Se te sugiere que te apropies del lenguaje matemático y le des sentido conforme se presenta la ocasión.
Aleatorio, azar, evento, excluyente o independiente son palabras que cobran particular importancia en el contexto de la probabilidad y las matemáticas.
Estudiar y conocer las características de la probabilidad ofrece ventajas para tomar decisiones. Por ejemplo, en el control de calidad de un producto se presentará una situación más para que reflexiones.
En una fábrica de tornillos hay tres máquinas con estas características:

La máquina A produce 30 % de los tornillos.
La máquina B fabrica 50 % de los tornillos.
La máquina C hace el otro 20 %.
Las tres máquinas juntas producen 4 % de tornillos defectuosos. Examina la probabilidad de elegir al azar un tornillo de cada máquina.
Reflexiona sobre la probabilidad de tomar al azar un tornillo fabricado por la máquina A y que no esté defectuoso.

De ser posible, comparte tus reflexiones con alguno de tus compañeros o compañeras.
El reto de hoy:
Resuelve por tu cuenta situaciones parecidas a las que aquí se te presentaron. Socializar tus resultados será de gran utilidad para consolidar los aprendizajes esperados.
Para poner en práctica lo aprendido, resuelve en tu libro de texto las actividades relacionadas con este aprendizaje esperado.
¡Buen trabajo!
Gracias por tu esfuerzo.





Login to join the discussion