Regla del producto I
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:22Aprendizaje esperado: resuelve problemas que implican calcular la probabilidad de eventos complementarios, mutuamente excluyentes e independientes.
Énfasis: obtener la regla del producto.
¿Qué vamos a aprender?
Necesitarás tu cuaderno de apuntes, lápiz y goma.
Para empezar, conocerás la probabilidad que cuando ocurre un evento A éste es independiente de que ocurra otro evento B.
Ya sea que ocurran los dos eventos al mismo tiempo o uno después del otro.
Se dice que estos eventos son independientes si la probabilidad de que el evento A suceda no está influenciada porque el evento B haya o no sucedido.
Ya sabes que la probabilidad clásica de que un evento A ocurra se calcula como:
P(A) = (Casos favorables / Casos Totales o posibles)
¿Qué hacemos?
Partirás un experimento clásico de la probabilidad, en donde lanzaremos un dado.
Sabes que la probabilidad de que, al lanzar un dado, caiga en el 3, es 1/6. Ahora, si vuelves a lanzar el mismo dado, ¿cómo es la probabilidad de que vuelva a caer otra vez el número 3? Es igual a la primera ocasión que lo hiciste, 1/6.

Esto es porque el evento anterior no tiene nada que ver con el segundo evento y, por lo tanto, las probabilidades de ocurrencia en ambos lanzamientos son las mismas.
Observa el segundo experimento aleatorio.
Se tienen dos cajas.
En la caja 1 hay 5 canicas rojas y 3 canicas verdes, sacas una canica, ¿cuál es la probabilidad de que una canica roja sea el evento A?
En la caja 2 hay 3 canicas rojas y 2 canicas verdes, extraes una canica. ¿Cuál es la probabilidad de que una canica roja sea el evento B?

La probabilidad del evento A, que es en la caja 1 sacar una canica roja es la cantidad de canicas rojas entre la cantidad de canicas.
P(A) = 5 entre 8.
La probabilidad del evento B, que es en la caja 2 sacar una canica roja es la cantidad de canicas rojas entre la cantidad de canicas.
P(A) = 3 entre 5.
Y la probabilidad de ocurrencia de A no influye en la probabilidad de ocurrencia de B.
Observa el siguiente video del inicio al minuto 04:04 en donde situarás con algunos ejemplos cómo se pueden presentar en el entorno y cómo los puedes identificar.
-
¿Cuándo dos eventos son independientes?
http://ventana.televisioneducativa.gob.mx/educamedia/telesecundaria/2/23/4/1369
Ahora, observa cómo puedes determinar o calcular la probabilidad de que ocurran estos eventos a partir de situaciones.

Inicia calculando algunas probabilidades. Comienza con la siguiente situación:
Sea A, el evento de que caiga sol.
¿Cuál es la probabilidad de que al lanzar una moneda caiga sol?
En este evento la probabilidad de ocurrencia está determinada porque en una moneda tienes dos posibles resultados: “águila” o “sol”, es decir el espacio muestral es
S = {águila, sol}
Así la probabilidad de ocurrencia del evento A es 1 de 2.
Si lanzas nuevamente la moneda, ¿qué probabilidad se tiene de que caiga nuevamente sol?
Analiza:
Se tiene que el espacio muestral de ambos lanzamientos queda determinado por los resultados:
S={(águila,sol),(águila,águila),(sol,sol), (sol,águila)}
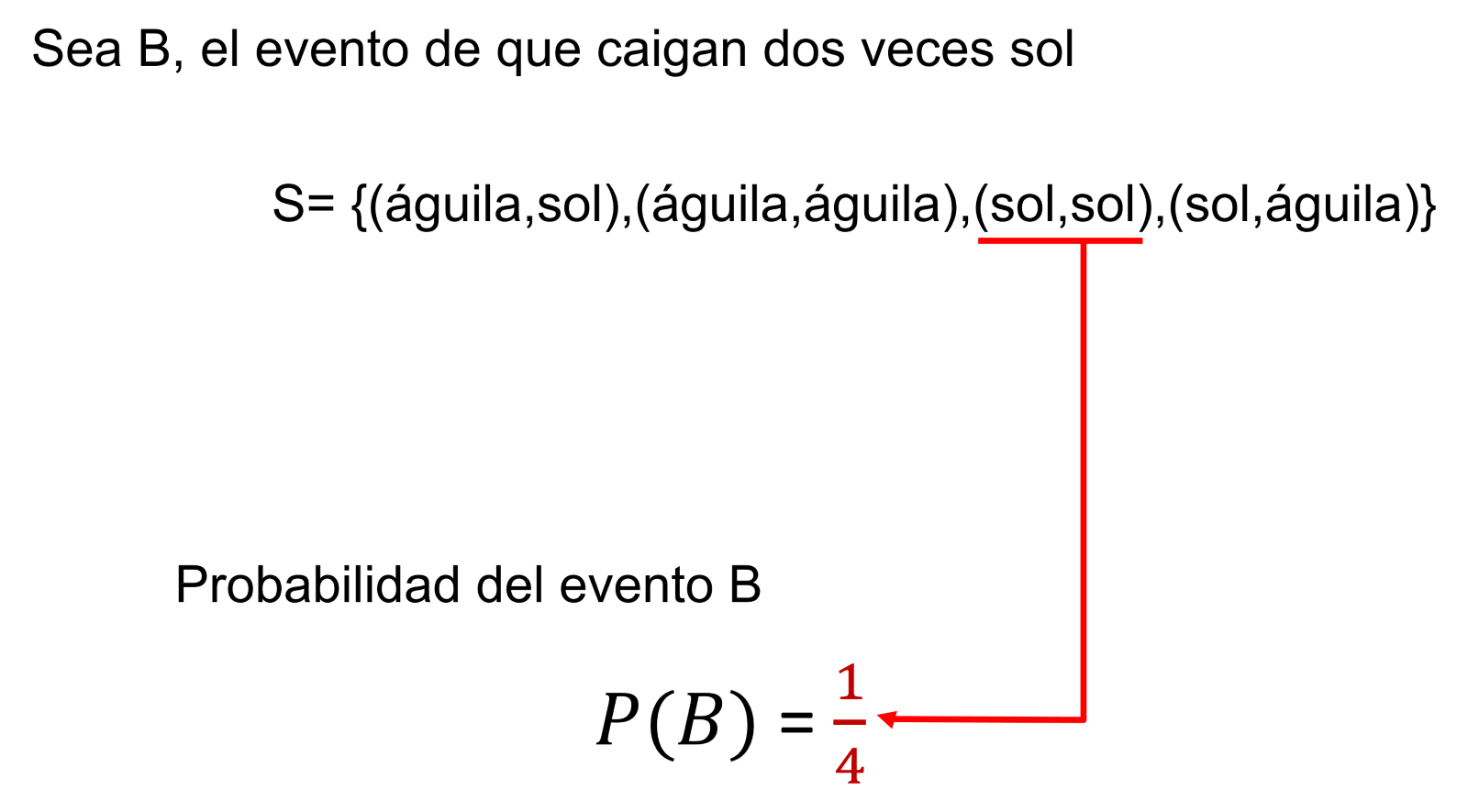
De ellos el que corresponde al de obtener “sol,” “sol” es una de 4 posibilidades, así la probabilidad de ocurrencia del evento B es de 1 cuarto.
Aumenta el número de lanzamientos.
Si se lanza una moneda tres veces. ¿Cuál es la probabilidad de que al caer en cada uno de los eventos caigan soles, es decir caiga 3 veces sol, sea éste el evento C?
Para esta situación elabora un diagrama de árbol.
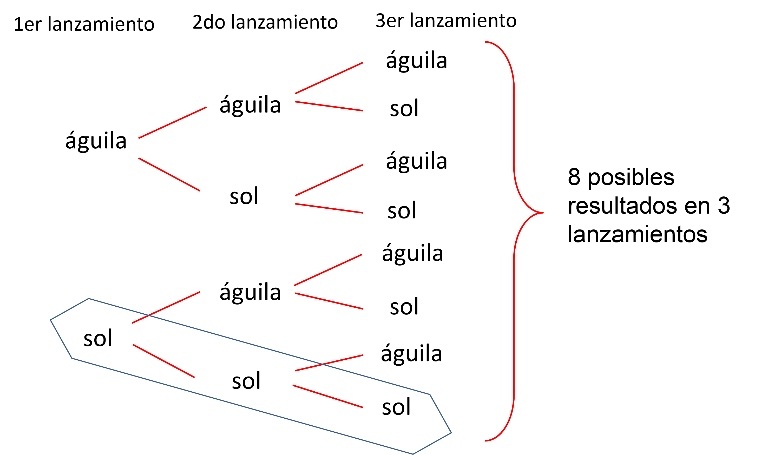
Se tiene que en el primer lanzamiento de la moneda puedes obtener “águila” o “sol”.
Se observa que para el segundo lanzamiento ya se tiene que sí se obtuvo “águila en el primero, ahora los resultados pueden ser (águila, águila) o (águila, sol) y si se obtuvo “sol en el primero, los resultados pueden ser (sol, águila) o (sol, sol).
Puedes observar que tienes 4 posibles resultados del evento.
De este modo, para el tercer lanzamiento tienes:
(águila, águila, águila)
(águila, águila, sol)
(águila, sol, águila)
(águila, sol, sol)
(sol, águila, águila)
(sol, águila, sol)
(sol, sol, águila)
(sol, sol, sol)
Se observa entonces que, de los 8 posibles resultados, uno es el que corresponde a obtener tres veces “sol”.
Entonces, la probabilidad de ocurrencia del evento C es 1 entre 8.

Reflexiona: el evento A es que en un lanzamiento se caiga sol y la probabilidad de ocurrencia es 1 entre 2.
El evento B es que se cumpla dos veces el evento A. Puedes hacer esta consideración porque aun cuando es el mismo evento, no influye la ocurrencia de uno sobre el otro.
Entonces: la probabilidad de ocurrencia del evento B es igual a 2 veces la probabilidad de ocurrencia del evento A.
Esto es: probabilidad del evento B es igual a dos veces la probabilidad del evento A, que es igual a P(A) por P(A), lo que hace que P(B) es igual a 1 entre 4.

Continua con la probabilidad del evento C, que es que salgan tres soles.

Como puedes darte cuenta, la obtención de la probabilidad de que un evento ocurra es independiente de que ocurran los otros dos, por eso la probabilidad que ocurra es el producto de los tres eventos.
Y la regla del producto coincide en lo observado en el diagrama de árbol: que obtener 3 soles es una de ocho posibles resultados. Así un octavo representa a esa probabilidad.

Puedes observar que, al aumentar el número de lanzamientos, la probabilidad de obtener sol en los 5 lanzamientos disminuyó en contraste con los primeros 3.
Hasta aquí has analizado y obtenido la probabilidad de que ocurra un evento independiente de forma simple. Observa ahora otro ejemplo diferente.
Pedro y José juegan a la perinola y acuerdan ganar bajo las siguientes condiciones:
Los dos tienen oportunidad de dos giros y ganan si los dos giros caen en lo que elige cada uno.
Pedro planea ganar si cae la cara “toma 1” y si cae en el segundo giro la cara, “toma 2”.
José planea ganar si cae “toma todo” en el primer giro y en el segundo giro “todos ponen”.
¿Cuál es la probabilidad de que Pedro gane?
¿Cuál es la probabilidad de que José gane?
Analiza para resolver:
La perinola tiene 6 caras con las siguientes opciones:
Toma1, toma 2, pon1, pon 2, toma todo y todos ponen.
De este modo, se tiene el siguiente arreglo rectangular que muestra el espacio muestral.
El arreglo rectangular muestra que para 2 giros de la perinola el espacio muestral está comprendido por 36 posibles resultados.
Ahora para que gane Pedro, quien debe obtener toma 1 y toma 2 en sus giros en ese orden, respectivamente, se tiene:

La probabilidad de ocurrencia es igual a:
Obtener “Toma 1” = 1/6
Obtener “Toma 2” = 1/6
Para A que representa los dos giros de Pedro
P(A)= 1/6 por 1/6 = 1/36

En el arreglo rectangular se observa lo que corresponde a la ocurrencia de obtener en el primer giro “toma todo” y en el segundo giro “todos ponen”.

Para el juego del amigo de Pedro se tiene:
Obtener “toma todo” es igual a 1/6
Obtener “todos ponen” es igual a 1/6
Así para B, que representa los dos giros del amigo de Pedro, se tiene:
P(B)= 1/6 por 1/6 = 1/36

Se concluye que la probabilidad de ganar al jugar la perinola es igual para Pedro y su amigo.
Trabaja ahora con el lanzamiento de un dado.

Observa un arreglo rectangular para representar el espacio muestral para el lanzamiento de dos dados.
Observa que para la pregunta del inciso A, se tiene que los casos favorables son:
{(3,1),(3,3),(3,5)}
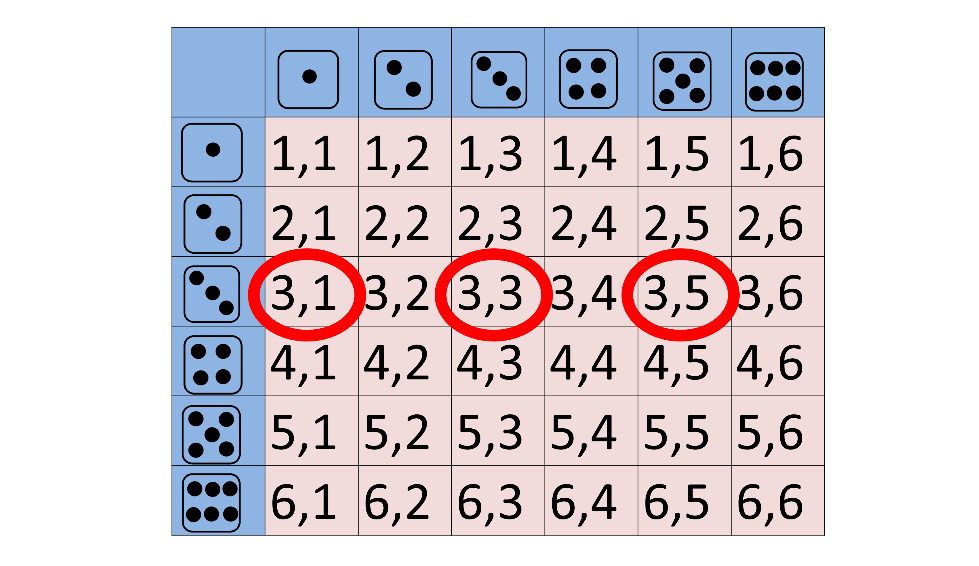
Se realiza el cálculo de la probabilidad.


La reflexión en este experimento es que es mayor la probabilidad de obtener un número primo y un número mayor que 4 comparado con obtener un número 3 y un impar, debido a que 1/6 > 1/12
Analiza las siguientes situaciones de tus compañeros de secundaria del interior del país.
Observa la siguiente situación que plantea Tania de la comunidad de Paredón en Chiapas.
-
Pescados y mariscos
Revisa el problema:
En un día normal la tía e Tania tiene a la venta, en promedio 6 kilos de macabil, 8 kilos de camarón, 12 kilos de mojarras y 10 kilos de ostión.
Si un cliente llega a comprarle.
A) ¿Cuál es la probabilidad de que le compre macabil y ostión?
B) ¿Cuál es la probabilidad de que le compre mojarras y camarón?
Analiza la primera pregunta:

Continua con la segunda pregunta.

Con esto se concluye que es más probable que le compren mojarras y camarón a que le compren macabil y ostión. Ya que:
2/27 > 5/108
Con este procedimiento obtienes la respuesta.
Ahora trabaja otra situación de una alumna de otra región, su nombre es Kenia de Tonalá, Chiapas.
-
El concurso
Según lo que plantea Kenia, ella participará en un concurso donde habrá 4 etapas, por lo tanto:

Esto lo puedes verificar en el siguiente diagrama de árbol.
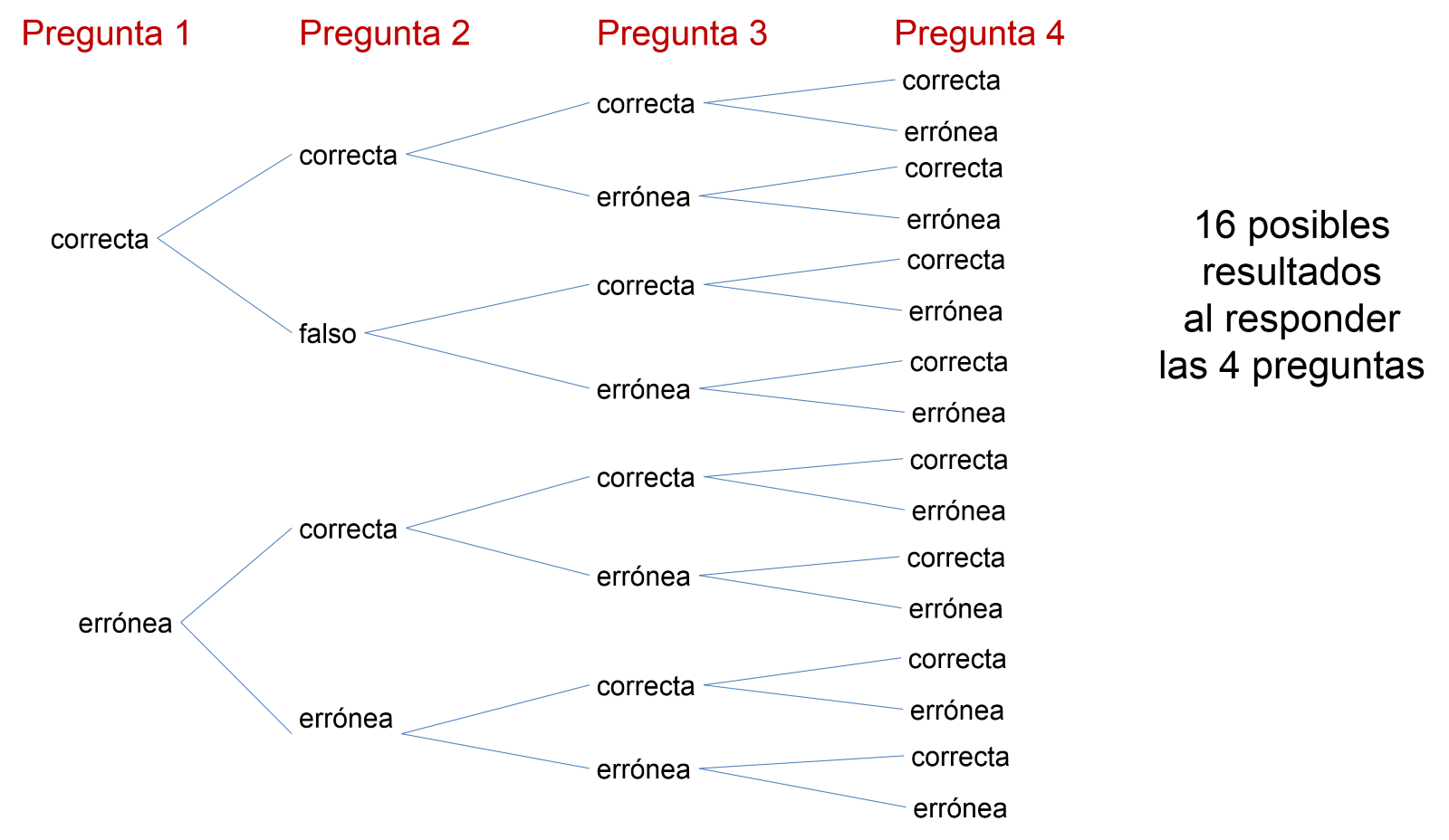
Para la pregunta 1 se tienen dos posibles respuestas: “correcta” o “errónea”.
Para la segunda pregunta ya has contestado una anterior, así que ahora el espacio muestral es:
(correcta, correcta), (correcta, errónea), (errónea, correcta), (errónea, errónea).
Así para cada pregunta el espacio muestral aumenta hasta llegar a que en la pregunta 4 se completa el total de 16 posibilidades.
La probabilidad de responder correctamente las 4 preguntas es de 1/16, considerando que cada pregunta tiene dos posibles respuestas que son correcta o errónea y una de ellas es correcta, según cada caso de modo independiente.
Así se considera que como todas deben ser correctas se tiene una única opción válida para ello.
Ahora para responder la segunda cuestión que plantea Kenia:
Si de esas 4 preguntas se equivoca en una, esto implica que tiene 3 preguntas correctas y una incorrecta, así tiene la oportunidad de la pregunta extra.
De este modo, de las 16 posibilidades antes descritas, se requiere ver cuántos son los casos favorables, pues debes ver cuál pregunta de las 4 resultó errónea.
Tienes la siguiente tabla, que muestra las posibilidades.

Puedes darte cuenta que se tienen 4 opciones en las que se muestra que existe una respuesta errónea a una de las preguntas. Entonces tienes 4 de 16 posibilidades, es decir, 4/16 que es igual a 1 entre 4.
Cabe resaltar que es mayor la probabilidad de tener un error en una pregunta que acertar a todas.
Esto explica que le des una pregunta extra para poder darle opción de avanzar en el concurso.
Ahora, con esas 4 opciones, al añadir la pregunta extra debes considerar la probabilidad de contestarla correctamente.
Ahora los posibles resultados son 32, pues son 5 preguntas, y no se debe olvidar que la respuesta sigue constando de las opciones de correcta o errónea a los cuestionamientos.
Calculando, se tiene:

La probabilidad del evento F es igual a la probabilidad de ocurrencia de los eventos D y E, esto es igual a un cuarto por un medio, que es igual a un octavo.
De lo anterior, se puede concluir que es más probable contestar 3 preguntas más la pregunta extra de forma correcta, que las 4 preguntas de manera correcta, ya que 1/8 es mayor que 1/16.
Cabe mencionar que en la segunda pregunta los eventos dejaron de ser independientes, debido a que la probabilidad de contestar la pregunta extra depende directamente de equivocar la respuesta de cualquiera de las 4 preguntas iniciales.
Para finalizar, resuelve la siguiente situación.
En una empresa laboran 70 mujeres y 80 hombres. Entre las mujeres hay 30 solteras y entre los hombres 18 solteros. Al entrevistar a un empleado al azar, ¿cuál es la probabilidad de que sea hombre y soltero?
En este caso considerarás a considerar que son eventos independientes.
La empresa tiene 150 empleados, que es el resultado de sumar 70 mujeres y 80 hombres.
Se quiere saber la probabilidad de que sea hombre y soltero, así:

En esta sesión aprendiste a identificar cuando un evento es independiente y cómo se determina la probabilidad de que ocurra aplicando la regla del producto.
El reto de hoy:
Revisa tu libro de texto para buscar los ejercicios correspondientes a este tema y consolida tus conocimientos.
Para terminar, recuerda una apostilla de Pierre Simón Laplace, sobre la probabilidad, que dice:
“En el fondo, la teoría de las probabilidades no es más que sentido común expresado en números”.
¡Buen trabajo!
Gracias por tu esfuerzo.
Descarga tu clase dando clic aquí





Login to join the discussion