Regla de la suma

Regla de la suma

Aprendizaje esperado: resuelve problemas que implican calcular la probabilidad de eventos complementarios, mutuamente excluyentes e independientes.

Énfasis: justificar la regla de la suma.

¿Qué vamos a aprender?

Aprenderás a calcular la probabilidad de que en un mismo experimento aleatorio se pueda determinar la probabilidad de que ocurra o no un evento.

Para iniciar revisarás algunos conceptos que ya conoces, con la finalidad de aplicarlos en el análisis de las situaciones que estudiarás. Primero, recuerda que la medida de la probabilidad es un valor entre cero y uno, incluyendo estos valores como posibles resultados.

¿Qué hacemos?

Un evento es un resultado específico de un experimento realizado al azar. Regularmente se le representa por las primeras letras del abecedario.

Por ejemplo…

Al evento de que al lanzar una moneda al aire y caiga águila lo denominarás “A”, mientras que al evento de que al lanzar la moneda y ésta caiga sol lo denominarás “B”.

Y escribes: P(A) es probabilidad de que ocurra el evento A, es decir, probabilidad de que caiga águila.

P (B) es probabilidad de que ocurra el evento B, es decir, probabilidad de que caiga sol.

Bien, ahora verás el concepto de eventos complementarios en la siguiente situación.

Cuenta con un primer evento al que denominarás evento “A”, para que el premio se lo lleve una niña.

Y tienes el evento “B”, para que el premio se lo lleve un niño

Responde las siguientes preguntas:

¿Existe otro evento que pueda ocurrir?

Los únicos eventos que pueden ocurrir, dado el experimento aleatorio, son los eventos A y B que estableciste y que constituyen el espacio muestral.

Recuerda que un espacio muestral es el conjunto de todos los posibles eventos que ocurren en un experimento aleatorio.

Para este ejemplo el espacio muestral es que el ganador sea un niño, o que la ganadora sea una niña.

Ya que conoces el espacio muestral, obtendrás la probabilidad de ambos eventos.

Para el evento “A”, calcularás su probabilidad mediante la fórmula clásica de la probabilidad, la cual sabes que se obtiene a través de la siguiente relación:

El número de casos favorables dividido entre el número total de casos posibles.

La probabilidad del evento A, que es la probabilidad de que el premio se lo lleve una niña, queda así:

La P(A) es igual a 18 dividido entre 30, que es igual a 0.6.

Es decir, la probabilidad de que ocurra el evento A es del 60 por ciento.

Ahora obtendrás la probabilidad de que ocurra el evento “B” y los pasos serán muy similares al caso anterior.

El evento B es que el premio se lo lleve un niño.

Entonces, P(B) es igual a dividir 12 entre 30, cuyo resultado es 0.4.

Es decir, la probabilidad de que ocurra el evento B es del 40 por ciento.

Con la medida de la probabilidad de ambos eventos se cubre en su totalidad el espacio muestral, es decir, 0.6 + 0.4 = 1.

Cuando esto ocurre, se dice que los eventos son complementarios. Es decir que los posibles resultados del primer evento y los posibles resultados del segundo evento cubren en su totalidad el espacio muestral del experimento aleatorio.

En el experimento aleatorio de lanzar una moneda al aire, los únicos eventos que pueden ocurrir son que caiga sol y que caiga águila, y estos dos eventos cubren todo el espacio muestral. Es decir, son eventos complementarios también.

Ahora ahondarás en las características de los eventos complementarios.

Lo primero que verás es que la suma de las probabilidades de un evento y de su complemento es 1.

Entonces: Si P(A) + P (complemento A) = 1

Entonces (PA) = 1 - probabilidad del complemento de A.

Comprueba lo que acabas de aprender con la experiencia aleatoria de la rifa del sombrero del mago.

Sabes que la probabilidad de ocurrencia del evento “A” es de 0.6 o de un 60%.

Aplica la fórmula que acabas de ver y realiza la operación 1 menos 0.6 que da como resultado 0.4, lo cual es lo mismo que 40%.

Como puedes darte cuenta, el resultado fue el mismo que si hubieses obtenido la probabilidad del evento “B” por la fórmula clásica.

Analiza otra situación y considera otro tipo de eventos.

¿Sabías que existen varios tipos de sangre?, y algunos son más comunes que otros.

Cuando se analiza la sangre se clasifica en 4 tipos sanguíneos (A, B, AB y O) y se identifica si tienen el factor Rh (positivo o negativo).

De acuerdo con los datos de la Cruz Roja Mexicana, en nuestro país se tienen los siguientes datos.

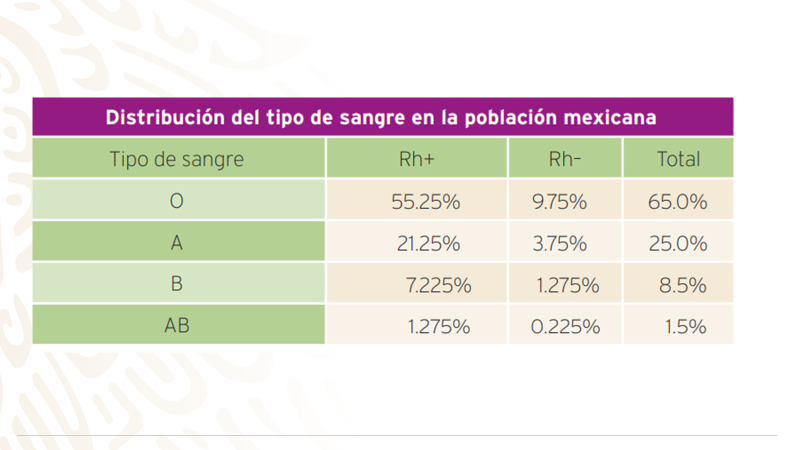
Puedes observar en la imagen la distribución del tipo de sangre en la población mexicana.

Determina la probabilidad asociada a cada uno de los siguientes eventos.

Para el evento que denominas “A”, que en este caso es la población que tiene sangre tipo O positivo, es del 55.25%.

Para el evento que denominas “B”, que es la población que tiene sangre tipo O negativo, es del 9.75%.

Y finalmente, el evento “C”, cuya población que tiene sangre tipo O, es de un 65 por ciento.

C es un evento compuesto, pues se construye a partir de dos eventos simples, como lo son los eventos A y B.

Ahora encuentra la probabilidad de ocurrencia de los eventos A, B y C.

Observa los datos otra vez. Y lo que notas es que cada una de las posibilidades excluye a las otras. Por ejemplo, si tienes sangre O positiva, no tienes sangre O negativa, ni sangre A positiva o negativa, ni B positiva o negativa ni AB positiva o negativa. Así, son eventos mutuamente excluyentes

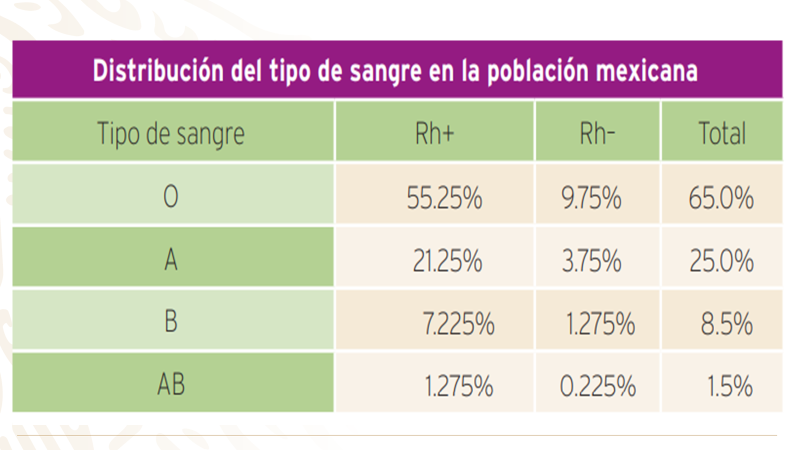
Entonces: la probabilidad del evento A es 55.25% y la probabilidad del evento B es 9.75%.

La probabilidad del evento “C” es igual a la suma de las dos probabilidades de los eventos que lo componen. Así, la probabilidad del evento “C” es 65%.

Para que quede más claro, tomarás como ejemplo un juguete mexicano, la pirinola, o perinola, en caso de que no la conozcas, te sugerimos que le pregunten a tus padres o abuelos.

El juego consiste en que cada participante tiene una cantidad de piedritas o fichas, entre otros elementos que son los que se van a tomar o agregar de acuerdo con lo que salga en la pirinola. Cada participante hace girar la pirinola que tiene 6 opciones y hace lo que indica la opción que cae.

Imagina que se lanza la pirinola, ¿cuáles son los eventos que pueden ocurrir?

Toma 1

Toma 2

Toma todo

Pon 1

Pon 2

Todos ponen

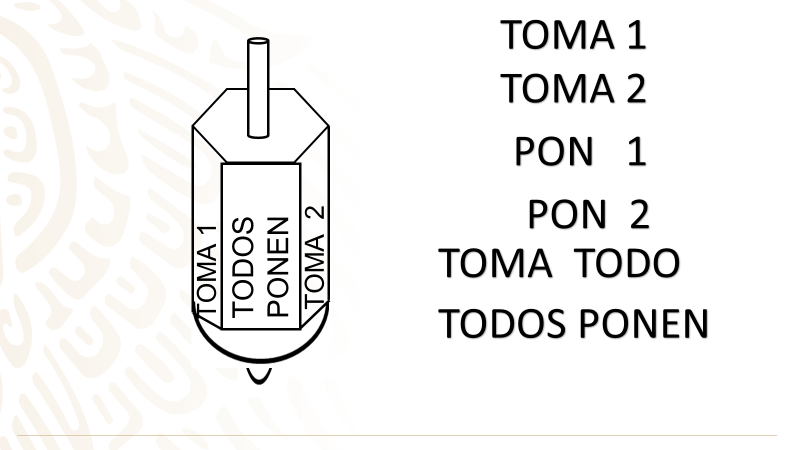
¿Hay alguna posibilidad o alguna forma de que ocurran 2 eventos de la pirinola al mismo tiempo?

No hay ninguna posibilidad, no es posible que en una pirinola ocurran dos eventos al mismo tiempo.

Por lo que puedes decir que estos eventos son mutuamente excluyentes.

Realiza el siguiente ejercicio: ¿Cuál es la probabilidad de que al lanzarla se obtengan las caras “Toma todo” o “Todos ponen”?, a los que llamarás evento A y evento B y el evento compuesto será el evento C.

Lo primero que notas es que hay una cara de cada uno de los eventos, por lo cual la probabilidad de que ocurra cada uno es:

1 entre 6

El resultado de ambos es aproximadamente de 0.166.

Y al igual que en el ejemplo anterior sumarás las dos probabilidades, es decir, 0.166 más 0.166

El resultado es 0.332

Por lo que puedes decir que la probabilidad de que ocurra el evento “A” o el evento “B” es de 33.2%

Así que como has podido ver, esta fórmula es la que has estado utilizando.

Y la relación escrita con palabras te dice que:

La probabilidad de obtener el evento A o el evento B es igual a la probabilidad del evento A más la probabilidad del evento B.

Esta relación es la regla de la suma, y te ayuda para encontrar la probabilidad de que ocurra un evento compuesto.

Una forma de poner en práctica lo que acabas de aprender, es realizando los siguientes problemas de probabilidad que han enviado distintas personas.

Problema 1.

Tengo un taller donde hay varios automóviles, y vamos a jugar una carrera en donde cada jugador elegirá su auto al azar. El punto es que hay 15 autos con una modificación en el sistema de escape, 12 autos a los que se les hizo una reprogramación, también hay 8 autos que cuentan con llantas especiales y 10 autos que no tienen ningún equipamiento. Ningún auto tiene dos de estas características.

La pregunta es la siguiente:

¿Cuál es la probabilidad de que al seleccionar al azar un auto, tenga uno con modificación en el sistema de escape o reprogramados?

Antes de continuar con el ejercicio, responde las siguientes preguntas:

1.- ¿Hay alguna posibilidad de que dos o más eventos ocurran al mismo tiempo?

No, no la hay.

2.- ¿Los eventos en cuestión cubren en su totalidad el espacio muestral?

En el problema se pregunta por la probabilidad de elegir al azar un auto, que éste tenga modificación en el sistema de escape o esté reprogramado. Estos dos eventos no abarcan la totalidad del espacio muestral, ya que no está contemplando los demás eventos.

3.- ¿Qué tipos de eventos puedes observar en este problema?

Observando las características puedes decir que son: mutuamente excluyentes, ya que no pueden ocurrir dos o más eventos al mismo tiempo

No puedes decir que sean eventos complementarios, ya que no abarcan totalmente el espacio muestral.

Ahora, repasa los datos que ya conoces

Ahora, procede a utilizar la fórmula de la regla de la suma, recuerda que dice que la probabilidad de que ocurra el evento A o el evento B es igual a la suma de las probabilidades de los dos eventos.

Por lo cual comenzarás con la probabilidad de ocurrencia del evento A, que en el enunciado dice que es la probabilidad de que un auto cuente con una modificación en el escape. Para este punto contarás con los siguientes datos:

15 autos con una modificación especial y en total hay 45 vehículos, por lo que la operación a realizar es:

15 entre 45, lo cual da como resultado aproximadamente 0.3333. Usarás tres cifras decimales, 0.333 Este número representa el 33.3%

El siguiente paso es obtener la probabilidad de ocurrencia del evento “B”, que es el resultado de dividir los eventos favorables entre el total de eventos, es decir, todos los autos que fueron reprogramados entre el total de autos.

Por lo que la operación es de 12 entre 45.

Lo que da aproximadamente como resultado 0.266, que equivale a 26.6%

Ahora obtén la probabilidad del evento C, que es seleccionar un auto que cuente con una modificación en el escape o que haya sido reprogramado.

Siendo eventos mutuamente excluyentes, sumarás las dos probabilidades.

El resultado de la suma es 15/45 + 12/45= 27/45, que es igual a 3/5, que es 0.6 o 60%

Ya tienes el resultado, la probabilidad de que elija un auto con modificación de escape reprogramado es de 60%

Problema 2.

Tenemos un problema en un barco. Hay latas de atún, salmón y pulpo, no hay latas que contengan más de una especie enlatada, sin embargo, el barco llegó a nosotros antes de que las latas pudieran ser etiquetadas, y dado que éstas son iguales no hay forma de saber qué tipo de contenido nos encontraremos hasta abrirlas.

El problema es que a ninguno de nosotros nos gusta el pulpo, y quisiéramos evitar desperdiciar latas de comida. ¿Hay alguna forma de saber cuál es la probabilidad de que la lata seleccionada sea de atún o de salmón?

Otros datos que se tienen es que encontramos el manifiesto de carga, este es un documento que nos dice exactamente qué carga trae el barco, y según este documento el cargamento contenía 1,130 latas, de las cuales: 320 latas son de atún, 430 latas son de salmón y 380 latas de pulpo.

Primero determina los eventos.

Sea A, el evento de que salga atún.

Sea B, el evento de que salga salmón.

Sea C, el evento de que salga atún o salmón.

Luego, observa que estás ante un problema que contiene eventos mutuamente excluyentes. Y el evento C es la unión de los eventos A y B. Lo resuelves por la regla de la suma.

Realiza la adición de la probabilidad de ambos eventos. Para obtener la probabilidad de que salga una lata de atún se realiza la operación 320 entre 1130.

Mientras que para obtener la probabilidad de que salga una lata de salmón se divide 430 entre 1130.

Para este punto debes decidir si harás la división como está escrita o realizarás alguna reducción o simplificación.

Puedes ver entonces que el resultado o probabilidad de que sea una lata de atún es de 0.283, lo que puedes traducir como 28%

Y la probabilidad de que sea una lata de salmón es de 0.380, lo que equivale a 38%

Como son eventos mutuamente excluyentes, ocuparás la regla de la suma para obtener la probabilidad del evento C, que es seleccionar una lata de atún o una lata de salmón.

La probabilidad de obtener una lata de atún o de salmón es igual a 28% + 38%, lo cual es igual a 66%

Recuerda las siguientes características: Los eventos complementarios cubren totalmente el espacio muestral, entendiendo como espacio muestral la totalidad de eventos que pueden ocurrir.

Los eventos mutuamente excluyentes no pueden ocurrir al mismo tiempo, es decir que, si el evento A ocurre, el evento B no puede ocurrir al mismo tiempo.

La regla de la suma te ayuda a obtener la probabilidad de eventos compuestos.

El reto de hoy:

En la siguiente imagen puedes ver varias figuras, las cuales se encuentran en una bolsa. Puedes observar que hay 12 figuras en total, entre las cuales hay diferentes formas y colores.

¿Podrías decir cuál es la probabilidad de que al azar y sin ver se obtenga de la bolsa un adorno rojo o azul?

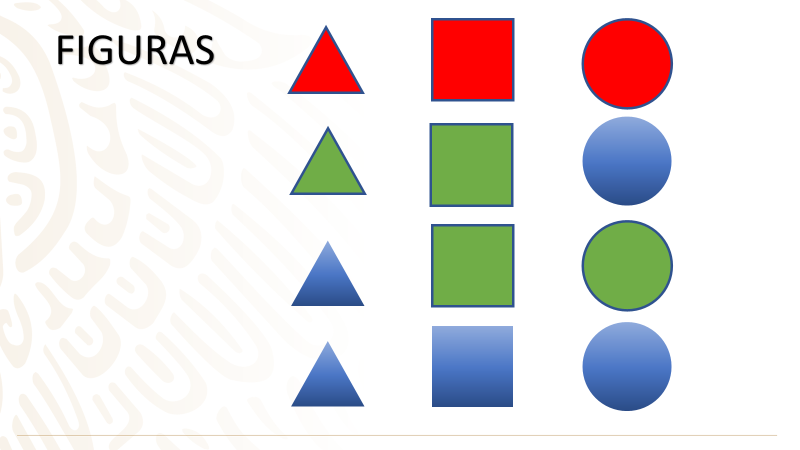
Realiza también un resumen de esta sesión.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

https://www.conaliteg.sep.gob.mx/