Razones trigonométricas II
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:23
Razones trigonométricas II
Aprendizaje esperado: resuelve problemas que implican el uso de las razones trigonométricas seno, coseno y tangente.
Énfasis: dar sentido y significado al comportamiento gráfico de las razones trigonométricas.
¿Qué vamos a aprender?
Estudiarás las funciones trigonométricas seno, coseno y tangente en el círculo unitario para obtener los valores más comunes y sus gráficas
Necesitarás tu cuaderno de apuntes, lápiz y goma.
Para comenzar, se conocen como razones trigonométricas a aquellas que relacionan los lados de un triángulo rectángulo.
Tres funciones trigonométricas son seno, coseno y tangente.
- Al cociente de la longitud del cateto opuesto entre la hipotenusa se le conoce como seno y se denota con la palabra “sen”.
- Al cociente de la longitud del cateto adyacente entre la hipotenusa se le conoce como coseno y se denota con la palabra “cos”.
- Al cociente de la longitud del cateto opuesto entre el cateto adyacente se le conoce como tangente y se denota con la palabra “tan”.
Ocuparás el círculo unitario para estudiar el comportamiento de estas funciones.
¿Qué hacemos?
Primero observa que en el estudio de los ángulos de un triángulo rectángulo hay unos que sirven de referencia, como son cero grados, 30, 45, 60 y 90 grados.
Ocupando el triángulo rectángulo, puedes calcular cuánto vale el seno, coseno y la tangente de algunos de los ángulos mencionados.
Completa la siguiente tabla.
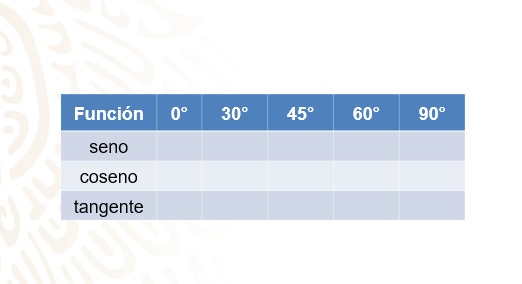
Supón que tienes un triángulo rectángulo cuyos catetos miden una unidad.

Esto significa que alfa mide 45 grados. Es así porque este triángulo rectángulo también es un triángulo isósceles. Entonces dos de sus ángulos miden lo mismo. Sabes que uno de los ángulos mide 90 grados porque es recto. Esto supone que la suma de los otros dos ángulos sea de 45 grados.
Ahora calcula cuánto vale la hipotenusa de este triángulo rectángulo. La hipotenusa es igual a la raíz cuadrada de la suma del cuadrado de los catetos, es decir, hipotenusa es igual a la raíz cuadrada del cateto opuesto al cuadrado más el cateto adyacente al cuadrado.
Esto hace que la hipotenusa sea igual a la raíz cuadrada de uno al cuadrado más uno al cuadrado.
La hipotenusa es igual a la raíz cuadrada de 2.
Ahora puedes encontrar cuánto vale el seno, el coseno y la tangente de 45 grados.
El seno de 45 grados es igual al cateto opuesto entre la hipotenusa; esto es, el seno de 45 grados es igual a uno entre raíz cuadrada de dos.
El coseno de 45 grados es igual al cateto adyacente entre la hipotenusa; esto es, el coseno de 45 grados es igual a uno entre raíz cuadrada de dos.
La tangente de 45 grados es igual al cateto opuesto entre el cateto adyacente; esto es, la tangente de 45 grados es igual a uno entre uno, lo que es igual a uno.
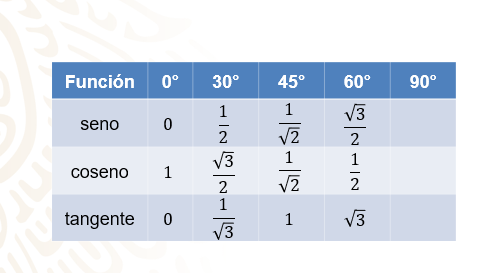
Escribe estos datos en la tabla.
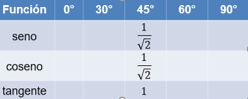
Encuentra los siguientes valores.
Considera un triángulo equilátero, cuya medida de cada lado es una unidad.
Como es un triángulo equilátero, cada uno de los ángulos mide 60 grados. Obtienes la altura de uno de los ángulos que, en este caso, divide al triángulo equilátero en dos triángulos rectángulos.
Considera el ángulo de 30 grados. La hipotenusa tiene un valor igual a una unidad. Uno de los catetos, el opuesto, es igual a un medio.
Para tener los datos necesarios, falta calcular el valor del otro cateto, el adyacente, que es la altura del triángulo.
El cateto adyacente al ángulo alfa es igual a la raíz cuadrada de la hipotenusa al cuadrado menos el cateto opuesto al cuadrado.
Sustituyes valores, es igual a la raíz cuadrada de uno al cuadrado menos un medio al cuadrado. Como un medio al cuadrado es igual a un cuarto, el cateto adyacente es igual a la raíz cuadrada de uno menos un cuarto, que es igual a la raíz cuadrada de tres cuartos. Esto es igual a la raíz cuadrada en el numerador y en el denominador.
Queda entonces que el cateto adyacente tiene un valor de raíz cuadrada de tres entre dos, y calcula.
El seno de 30 grados es igual al cateto opuesto entre la hipotenusa; esto es, el seno de 30 grados es igual a un medio.
El coseno de 30 grados es igual al cateto adyacente entre la hipotenusa; esto es, el coseno de 30 grados es igual a raíz cuadrada de tres entre dos.
La tangente de 30 grados es igual al cateto opuesto entre el cateto adyacente; esto es, la tangente de 30 grados es igual a uno entre raíz cuadrada de tres.
Escribe estos datos en la tabla.
Sigue con el triángulo equilátero anterior, sólo que ahora considera el ángulo de 60 grados de uno de los dos triángulos rectángulos.
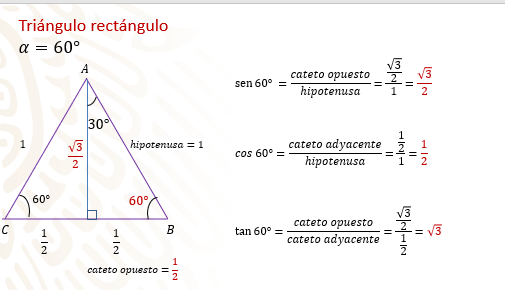
Por los cálculos anteriores ya tienes cuánto mide el cateto opuesto al ángulo de 60, raíz cuadrada de tres entre dos, y calcula.
El seno de 60 grados es igual al cateto opuesto entre la hipotenusa; sustituye valores y queda raíz cuadrada de tres entre dos entre uno, esto es, el seno de 60 grados es igual a raíz cuadrada de tres entre dos.
El coseno de 60 grados es igual al cateto adyacente entre la hipotenusa. Al sustituir valores, queda que es igual a un medio entre uno, esto es, el coseno de 60 grados es igual a un medio.
La tangente de 60 grados es igual al cateto opuesto entre el cateto adyacente. Sustituyes valores, queda como raíz cuadrada de tres entre dos, entre un medio. Queda entonces que la tangente de 60 grados es igual a raíz cuadrada de tres.
Escribe estos datos en la tabla.
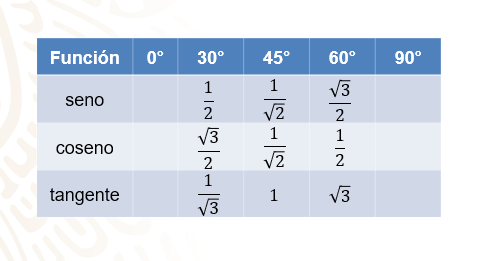
Hace falta encontrar los valores para los ángulos de cero grados y de 90 grados.
Para ello, se ocupará el círculo unitario.
Se llama círculo unitario al círculo de radio uno, utilizado para representar las razones trigonométricas y obtener de forma gráfica los valores de las funciones con respecto a un ángulo dado.
Las razones trigonométricas en el círculo unitario se construyen de la siguiente manera:
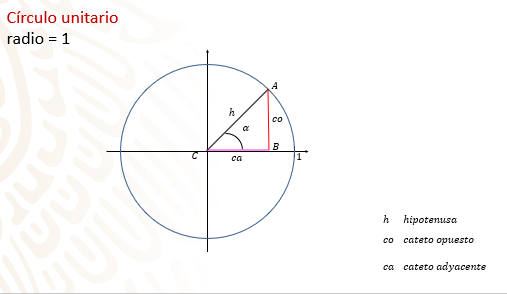
- En el plano cartesiano se traza un círculo de radio igual a uno. Este es el círculo unitario.
- Se traza un segmento de recta que va del centro “C” a cualquier punto de la circunferencia, por ejemplo, “A”, siendo el radio del círculo el segmento “CA”.
- Se traza la vertical que pasa por “A” y corta el eje de la “x” en el punto “B”.
- Se traza el segmento “CB”.
- Se marca el ángulo, al que llamarás alfa.
Se ha formado dentro del círculo unitario el triángulo rectángulo “ACB”.
El radio “CA” es la hipotenusa, la llamaremos “h”.
El lado “AB” es el “cateto opuesto al ángulo alfa.
El lado “CB” es el cateto adyacente al ángulo alfa.
Del círculo unitario tienes que el seno de alfa es igual al cociente del cateto opuesto sobre la hipotenusa.
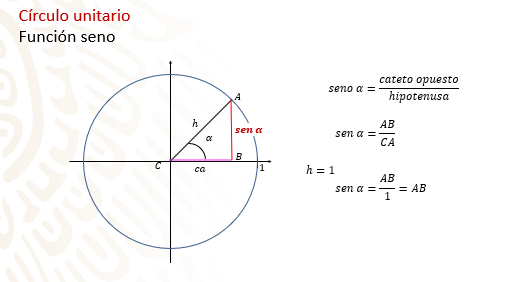
Es decir, el lado “AB” entre “CA”; como el lado “CA” es el radio de la circunferencia y es igual a 1, el seno de alfa es igual al lado “AB”.
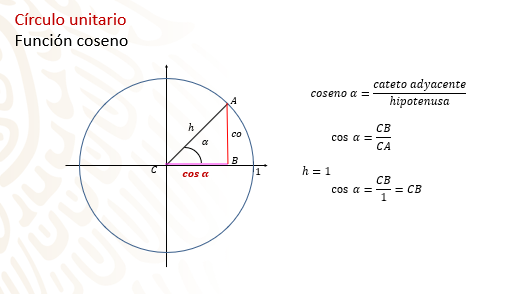
El coseno de alfa es igual al cociente del cateto adyacente sobre la hipotenusa.
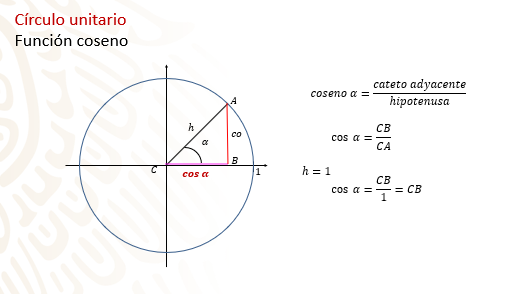
Es decir, el lado “CB” entre “CA”, como el lado “CA” es el radio de la circunferencia y es igual a 1, el coseno de alfa es igual al lado “AB”.
La tangente de alfa es igual al cociente del cateto opuesto sobre el cateto adyacente.
Así, la tangente de alfa es igual a “AB” entre “CB”.
Ya se definió el círculo unitario y las funciones seno, coseno y tangente con respecto a un ángulo alfa.
Regresa a calcular el valor del seno, coseno y tangente de los ángulos cero y 90 grados, ahora ocupando el círculo unitario.
Si alfa es igual a “0” grados, esto implica que el punto “A” se encuentra sobre el eje de las “x” y que el cateto “AB” es igual a cero, mientras que la hipotenusa que tiene el valor del radio sigue siendo igual a uno.
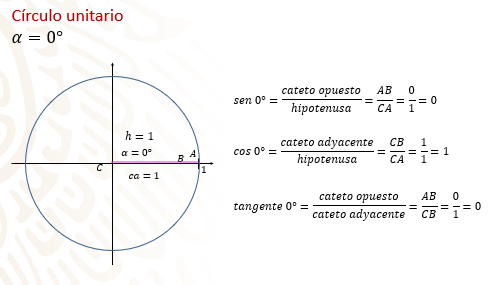
Así, seno de cero grados es igual a cero entre 1, lo que lo hace igual a cero.
Para el coseno de cero grados, “B” se encuentra en el punto 1 sobre el eje de las “x”, entonces el cateto adyacente “CB” tiene valor de uno. Así, el coseno de cero grados es igual a uno entre uno, lo que lo hace igual a uno.
La tangente de cero grados es igual a cero entre uno, lo que lo hace igual a cero.
Escribe estos datos en la tabla.
Ahora observa el caso cuando alfa es igual a 90 grados.
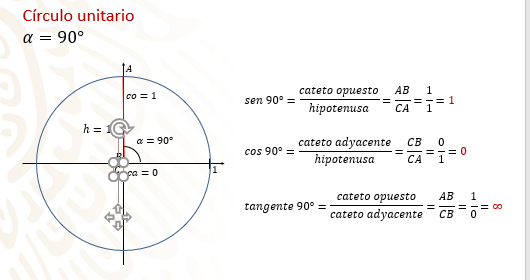
El que alfa sea igual a 90 grados implica que el punto “A” se encuentra sobre el eje de las “y” y que el cateto “AB” es igual a uno, mientras que la hipotenusa, que tiene el valor del radio, sigue siendo igual a uno.
Así, seno de 90 grados es igual a uno entre uno, lo que lo hace igual a uno.
Para el coseno de 90 grados, “B” se encuentra en el origen, el punto cero del eje de las “y”, entonces el cateto adyacente “CB” tiene valor de cero. Así, el coseno de 90 grados es igual a cero entre uno, lo que lo hace igual a cero.
La tangente de 90 grados es igual a uno entre cero, lo que lo hace igual a infinito.
¿Por qué es así? ¿Cuál será el cociente de uno entre un número pequeño?
¿Cuánto es uno entre 0.5? Es 2. ¿Entre 0.25? Es 4. Entre 0.01 es 100. Entre 0.001 es 1 000.
Y así puedes seguir, de tal manera que el resultado de la división de uno entre una cantidad pequeña es un número cada vez más grande.
Y conforme te vas acercando a cero, el resultado es cada vez más grande. De tal manera que muy cerca de cero ya no puedes definir qué cantidad es, y por eso lo llamas infinito.
Ahora escribe estos datos en la tabla. Y con eso la completas.
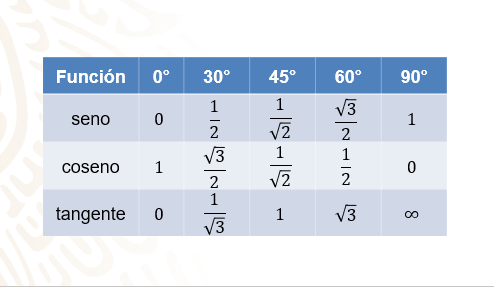
Ahora observa estas cantidades en números decimales.
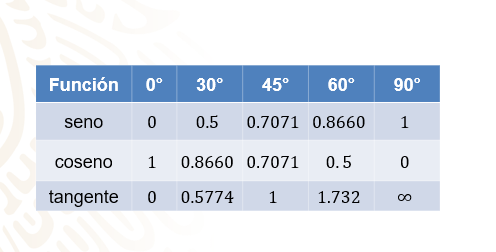
Así como toda expresión matemática tiene una representación gráfica, también las funciones trigonométricas tienen una representación gráfica en la que puedes ver el comportamiento de estas funciones.
Observa la gráfica de la función y = sen “x”, dando valores a “x” desde cero grados hasta 360 grados.
En el lado izquierdo de la gráfica se observa el círculo unitario donde se indica el ángulo en grados, y del lado derecho en el plano cartesiano está la gráfica de la función seno de dicho ángulo.
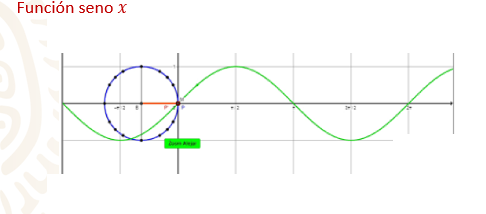
Observa cómo, al iniciar en el ángulo cero grados, la gráfica de seno en el plano cartesiano inicia en el origen.
Al llegar a 90 grados el ángulo, se alcanza el nivel máximo de la gráfica, es decir, el valor de “y” es 1.
Al seguir aumentando los grados del ángulo, la gráfica en el plano cartesiano disminuye hasta llegar a cero cuando el ángulo es igual a 180 grados.
A partir de los valores de los ángulos mayores a 180 grados, los valores de la función en la gráfica son negativos, teniendo el punto mínimo en 1 negativo cuando el ángulo es igual a 270 grados, y finalmente al llegar a 360 grados el valor de la función es cero.
En la gráfica se observan los valores para la función coseno.
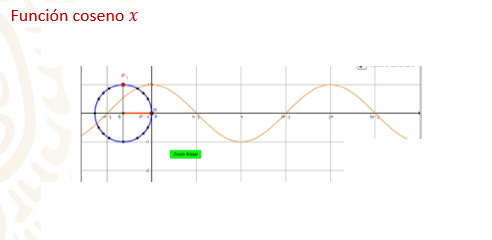
En cero grados el valor de la función es 1, y va decreciendo hasta llegar al valor 1 negativo conforme aumenta el ángulo a 180 grados.
A partir de ahí, al crecer el ángulo en grados, los valores de la función coseno crecen hasta llegar nuevamente al valor de 1 cuando el ángulo es de 360 grados.
En la gráfica de la función tangente se observa que para el ángulo de cero grados el valor es cero.
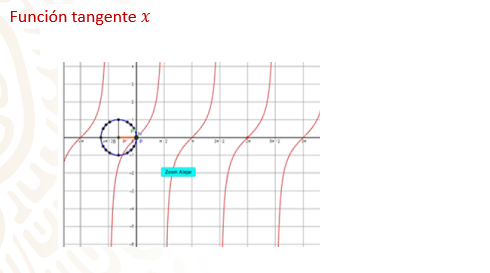
Observa cómo los valores de la tangente para los ángulos 90 y 270 grados no está definida, tal como se mencionó anteriormente. Mientras que el valor de la función tangente para los ángulos cero, 180 y 360 grados es de cero.
Observa el siguiente video del minuto 02:22 a 02:53 y del 03:32 a 10:45
- Aplicación de las razones trigonométricas
https://www.youtube.com/watch?v=VPBqyh5rH9U
El tema es amplio y requiere más estudio. Pero sí debes considerar que las razones trigonométricas se aplican en áreas del conocimiento como la topografía, donde permiten calcular la altura de un edificio dada la base y el ángulo.
En aviación se puede determinar la distancia de dos aviones que partieron a la misma velocidad y siguieron trayectorias rectas.
Y también es fundamental para guiar el rumbo correcto de un barco.
En la ingeniería se utiliza para construir puentes a través de las montañas y lograr que las atraviesen correctamente.
El reto de hoy:
Analiza las siguientes preguntas de reflexión.
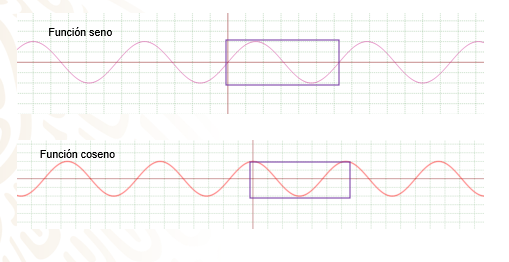
- La gráfica de la función seno es cíclica, es decir, se repiten los valores al considerar los 360 grados del círculo unitario. ¿Cuántos grados medirá el ángulo cuando el valor de la función seno es cero en la parte indicada en la gráfica?
- En el caso de la gráfica de la función coseno, el valor para el ángulo 275 grados, ¿es positivo o negativo? ¿y para el ángulo de 99 grados?
- En el caso de la gráfica de la función tangente, el valor para el ángulo de 99 grados, ¿está definida?
Revisa tu libro de texto para buscar los ejercicios correspondientes a este tema y consolides tus conocimientos.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas






Login to join the discussion