Raíz cuadrada por medio de aproximaciones
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:07Raíz cuadrada por medio de aproximaciones
Aprendizaje esperado: resuelve problemas de potencias con exponente entero y aproxima raíces cuadradas.
Énfasis: interpretar el significado de obtener raíces cuadradas y calcularlas por medio de aproximaciones.
¿Qué vamos a aprender?
En esta lección aprenderás a interpretar el significado de obtener raíces cuadradas y a calcularlas por medio de aproximaciones.
¿Qué hacemos?
Para comenzar con el tema que se estudiará el día de hoy, y para conocer un poco de los antecedentes del concepto de la raíz cuadrada, analiza la información del siguiente audiovisual.
- La raíz cuadrada.
https://www.youtube.com/watch?v=BLYO3kd1rsE
Revisa del tiempo 00:26 al 01:44.
¿Qué te pareció?
Como viste, es interesante saber que los antiguos egipcios y griegos ya conocieran la raíz cuadrada y que le dieran un uso práctico. Ahora, se recuperará del audiovisual el significado de la raíz cuadrada.
La raíz cuadrada de un número “equis” es otro número “a” tal que al elevarlo al cuadrado da “equis”. Como en el ejemplo del audiovisual, la raíz de 81 es igual a nueve, porque nueve al cuadrado es ochenta y uno.
De acuerdo con la información del audiovisual, ¿cómo surgió la raíz cuadrada?
La respuesta es que surgió al plantear problemas geométricos, como el cálculo de la longitud de la diagonal de un cuadrado.
Recuerdas, ¿cuál fue el descubrimiento de Pitágoras?
Pitágoras planteó que la raíz cuadrada de 2 es aproximadamente 1.4142, que es un número irracional, es decir un número cuya parte decimal es infinita y no periódica, y ésta no se puede representar como el cociente de dos números enteros.
Ahora verás cómo se calcula la raíz cuadrada, y después conocerás algunas de sus propiedades. Para ello se te invita a ver el siguiente material audiovisual, llamado: “raíz cuadrada de un número”. - Raíz cuadrada de un número.
https://www.youtube.com/watch?v=DeBcEu3px6I
Revisa del tiempo 00:37 al 05:13.
Analiza los aspectos de la raíz cuadrada que puedes recuperar de este segundo audiovisual. Primero se habló de una propiedad importante de la raíz cuadrada: que sacar la raíz cuadrada y elevar al cuadrado son operaciones inversas.
¿Qué significado puedes darle a dicha propiedad?
Que lo que una operación hace, la otra lo deshace, revisa un ejemplo:
Si a 64 le aplicas la operación de raíz cuadrada, obtienes como resultado ocho. Pero para regresar de 8 a 64 la operación que tienes que hacer es elevar al cuadrado a 8 y obtendrás 64.
Después, se habló de una de las aplicaciones de la raíz cuadrada. Así es, se mencionó que la raíz cuadrada es útil para calcular el lado de un cuadrado de área conocida.
Un ejemplo adicional, al que observaste en el audiovisual, sería ¿cómo calcular el lado de un terreno cuadrado que tiene un área de 2500 metros cuadrados?
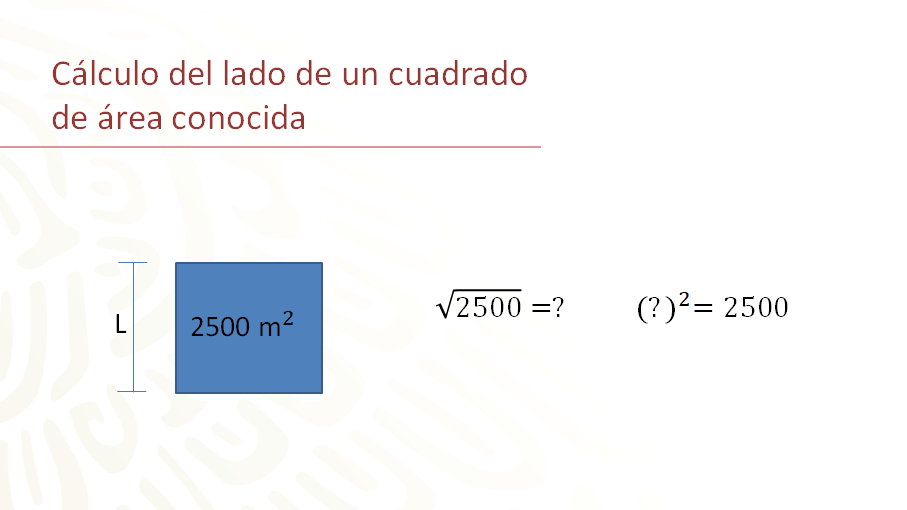
Para encontrar el resultado tienes que obtener la raíz cuadrada de 2500 metros cuadrados.
¿Cómo encuentras la raíz cuadrada de 2,500?
Equivale a encontrar un número que al elevarlo al cuadrado dé como resultado 2500 metros cuadrados.
¿Cómo encuentras ese número?
¿Cómo se obtuvo la raíz cuadrada en el audiovisual?
Este sería el tercer aspecto que observaste en el audiovisual, el del método de aproximaciones sucesivas para encontrar una raíz cuadrada.
¿En qué consiste este método?
Consiste en proponer un número entero, elevarlo al cuadrado e inspeccionar si es mayor o menor al número al que le sacarás la raíz, y repetir el procedimiento hasta acercarte lo suficiente al resultado.
Por ejemplo, utiliza este método de aproximaciones sucesivas para encontrar la raíz cuadrada de 2,500.
En el audiovisual se dijo que 40 al cuadrado es 1600, entonces la raíz de 2500 tiene que ser mayor que 40.
Se hace una aproximación al resultado, utilizando 60.
Como 60 al cuadrado es 3600, entonces para obtener 2500 se tendrá que multiplicar por sí mismo un número menor a 60 pero mayor que 40.
Por inspección, se puede ver que 2500 termina en dos ceros, entonces puede ser un múltiplo de 10, y la raíz tendría que terminar en cero. Así que se tomará al número 50 y hay que verificar si cumple con la condición que se mencionó.
50 al cuadrado es igual a 50 por 50 igual a 2500.
Así que la raíz cuadrada de 2500 es 50, porque 50 al cuadrado es igual a 2500.

Después de este ejercicio hay profundizar en qué consiste el método de aproximaciones sucesivas. Para eso, hay que resolver otra raíz cuadrada con este método.
¿Cómo se encuentra la raíz cuadrada de 15,376?
El método se basa en conocer los cuadrados de números enteros y después ver qué número se aproxima a la raíz cuadrada hasta encontrarlo.
Se puede iniciar proponiendo un número, por ejemplo, comenzar con 60 como raíz, y su cuadrado es 3600, pero la raíz debe ser mayor, así que se propone a 100 como raíz, y su cuadrado es 10,000.
Nota que se está aproximando, así que se continúa proponiendo otra raíz, ahora se toma al número 200, cuyo cuadrado es 40,000. Ya se pasó, ahora sabes que la raíz debe estar entre 100 y 200. Si utilizas un valor medio, como 150, tienes que 150 al cuadrado es igual a 22500.
La raíz está entre 100 y 150. Si utilizas un valor medio como 125, ahora su cuadrado es 15625. Ya estás muy cerca, la raíz que estás buscando está alrededor de 125.
Como 15,376 acaba en número par 6, sus posibles raíces son múltiplos de 2; es decir que su raíz es par, pero también 15,376 termina en 76, que es múltiplo de 4.
Así que un número menor, y cercano a 125, que sea par y a su vez sea múltiplo de 4, podría ser 124 o 120. 120 al cuadrado es 14,400, entonces hay que probar con 124, 124 al cuadrado es 15,376. La raíz cuadrada de 15,376 es igual a 124.

Se encontró este resultado por medio de las aproximaciones sucesivas.
Bien, ¿qué otro aspecto falta por recuperar del audiovisual?
Faltaría recuperar dos propiedades de la raíz cuadrada.
La primera consiste en que la raíz cuadrada de un producto es igual al producto de sus raíces.
Por ejemplo, la raíz cuadrada de 2500 se puede expresar como la raíz cuadrada de 25 por 100, que a su vez es igual al producto de la raíz cuadrada de 25 por la raíz cuadrada de 100.
Esto es, la raíz de 25 es 5 y la raíz de 100 es 10, se multiplican las raíces, 5 por 10 igual a 50, que corresponde a la raíz que se encuentra aplicando el método de aproximaciones sucesivas.

La segunda propiedad es muy parecida, porque como sabes la multiplicación y la división son operaciones inversas. Así que: la raíz cuadrada de una fracción es igual a la raíz cuadrada del numerador entre la raíz cuadrada del denominador.
Por ejemplo, la raíz cuadrada de 15,376 cuartos es igual a la raíz de 15,376 entre la raíz de 4. Se sacan ambas raíces y ya sabes que la raíz cuadrada de 15,376 es 124 y la raíz cuadrada de 4 es 2, así que te da como resultado la fracción 124 medios, que es equivalente al número 62.
También puedes haber realizado primero la división, antes de obtener la raíz cuadrada, entonces 15,376 entre 4 es igual a 3,844. Y la raíz cuadrada de 3,844 es igual a 62.

Con estas propiedades, tienes una forma alterna de comprobar tus resultados.
Se espera que hasta este momento sean claros los planteamientos que se han recuperado del segundo audiovisual y que has ampliado para tu estudio.
Para comprender mejor y facilitar la búsqueda de una raíz cuadrada con el método de las aproximaciones sucesivas, puedes utilizar una tabla que contenga diferentes números enteros y sus cuadrados.
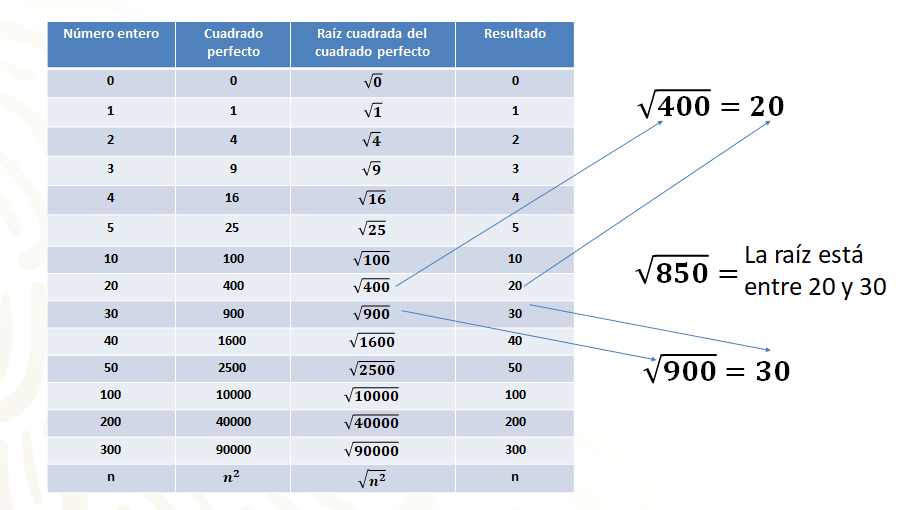
Revisa la siguiente tabla, en la que se anotó el número entero, por ejemplo, cero, uno, dos, tres, diez, veinte, treinta, cuarenta, cincuenta, 100, doscientos, trescientos, hasta ene cuadrada.
En la segunda columna estará el cuadrado de ese número entero, por ejemplo, cero al cuadrado es cero, cinco al cuadrado es 25, cuarenta al cuadrado es 1600, 100 al cuadrado es diez mil y ene al cuadrado es ene cuadrada.
En la tercera columna se tiene la raíz cuadrada de cada entero al cuadrado, como la raíz de cero es cero, la raíz cuadrada de 25 es 5, la raíz cuadrada de 1600 es 40 y la raíz cuadrada de ene cuadrada es ene.
Observa que, en la tabla, primero se elevó un número al cuadrado y después se le sacó la raíz cuadrada y se obtuvo el mismo número entero.
Esta acción de elevar al cuadrado un número y después aplicarle su raíz para regresar al mismo número es gracias a que las operaciones, como ya se mencionó, son inversas.
Pero ¿para qué se hizo esto?
Para construir un concepto que tiene que ver con la raíz cuadrada. El concepto de un cuadrado perfecto. Todos los números de la tabla que al sacarles raíz cuadrada dan como resultado un número entero, se dice que son cuadrados perfectos, como, por ejemplo, los números que se han utilizado en los ejemplos, tanto en los audiovisuales como durante la sesión:
Cero, uno, cuatro, nueve, dieciséis, veinticinco; y se puede seguir así construyendo la sucesión y encontrarás los números: 36, 64, 81, 100, 144, 1296, 2500, 3025, 4489.
¿Qué puedes concluir de la raíz cuadrada de números enteros al cuadrado?
La respuesta es que la raíz cuadrada de un número mayor o igual que cero es otro número que, al elevarlo al cuadrado, te da el número original. Es decir, “a” es la raíz cuadrada de “x”, si “a” al cuadrado es igual a equis.
En el caso de la tabla que se construyó, puedes ver que la raíz cuadrada de 400 es igual a 20 y la raíz cuadrada de 900 es 30, así que, si buscas la raíz cuadrada de un número intermedio, como 850, su raíz estará entre 20 y 30. Así que aquí es donde podrás hacer tu primera propuesta para el método de aproximaciones sucesivas.
Ahora, falta hablar de otro aspecto importante de la raíz cuadrada.
¿Tú crees qué una raíz cuadrada tiene dos resultados?
La raíz cuadrada de un número cuadrado perfecto mayor que cero tiene como resultado dos números enteros simétricos. Por ejemplo, se ha calculado la raíz cuadrada de los siguientes números:
Raíz cuadrada de 4 es 2 porque 2 al cuadrado es cuatro. Pero también dos negativo al cuadrado es cuatro.
Por lo tanto, al sacar la raíz de un cuadrado perfecto mayor que cero, el resultado será un entero y su simétrico.
Observa estos otros ejemplos:
La raíz cuadrada de 100 es 10 porque 10 al cuadrado es cien, pero también es 10 negativo, porque 10 negativo al cuadrado es igual a 100.
Encontraras muy probablemente, en tu libro de texto, las siguientes expresiones:
Raíz cuadrada de 25 es igual a 5, o
Raíz cuadrada de 25 es igual a 5 negativo, o
Raíz cuadrada de 25 igual a más menos cinco.

Esto quiere decir, precisamente, que la raíz cuadrada tiene dos resultados: el positivo y el negativo.
Pero, ¿qué pasa con la raíz cuadrada de cero?
En este caso la raíz cuadrada de cero es simplemente cero porque cero al cuadrado es igual a cero. Falta analizar el caso en que se pretende obtener la raíz cuadrada de un número negativo.
Si tienes a la mano una calculadora puedes, por ejemplo, pulsar la tecla de raíz cuadrada, ingresar 36 negativo y pulsar la tecla igual. ¿Qué resultado arroja la calculadora?
Si tuviste la oportunidad de hacerlo, habrás encontrado un mensaje de error. ¿Qué significa esto?
Que en el conjunto de números que has utilizado no hay una respuesta. Ya que no existe un número que al elevarlo al cuadrado tenga un resultado negativo.
Si se eleva 6 al cuadrado se obtiene el número 36.
Si se eleva -6 al cuadrado se obtiene también 36, pero no obtienes 36 negativo.

Por lo pronto, hay quedarse con el hecho de que, en los números reales, que son los que has venido usando, no hay un resultado para las raíces cuadradas de números negativos.
En tus cursos posteriores de matemáticas encontrarás que esta operación es posible dentro de otro conjunto numérico.
Bien has concluido el tema del día de hoy. Recuerda estudiar con mayor profundidad este tema en tu libro de texto de segundo grado.
El reto de hoy:
Para finalizar, se propone que realices el reto mostrado en el segundo audiovisual: Encuentra la raíz cuadrada de 3025 con el método de aproximaciones sucesivas y la raíz cuadrada de la fracción 144 entre 4, utilizando las propiedades de la raíz cuadrada.
Además, se te invita a que trates de responder la pregunta del final del segundo audiovisual: ¿La raíz de una suma será igual a la suma de sus raíces?
Comparte tus reflexiones con tus compañeras, compañeros y docentes.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion