¿Quién es el más alto?
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 16:42Aprendizaje esperado: identificación de una fracción o un decimal entre dos fracciones o decimales dados. Acercamiento a la propiedad de densidad de los racionales, en contraste con los números naturales.
Énfasis: resuelve problemas que implican comparar fracciones y decimales.
¿Qué vamos a aprender?
Aprenderás a resolver problemas que implican comparar fracciones y decimales.
¿Qué hacemos?
Actividad 1:
En esta sesión participaras en un juego muy divertido, se trata de que compares números fraccionarios y decimales; para esto, es importante que tengas a la mano tu libro de Desafíos Matemáticos de sexto grado, y que lo abras en la página 72, en donde se encuentra el Desafío 35; consigue una hoja o cuaderno para tomar notas, lápiz y goma.
https://libros.conaliteg.gob.mx/20/P6DMA.htm?#page/72

Para jugar, necesitarás cuatros dados grandes, 2 cintas métricas, pizarrón y marcadores.
Se requieren dos dados con fracciones y dos dados con decimales para hacer el juego más interesante.

El juego consiste en que tirarás los dados, luego, escribe los resultados obtenidos en una tabla como la siguiente y, después responde a la pregunta: ¿Qué cantidad es más grande? Después, comprueba los resultados.
| Participante | Dado 1 | Dado 2 | ¿Qué cantidad es más grande? |
Como puedes observar, el primer dado mostró ¼ y luego el segundo dado obtuvo 1/3, ¿qué fracción es más grande?
Es correcto: 1/3.
Ahora supondrás que en los dados aparece 0.5 y 0.1 ¿Cuál es el más grande de estos dos números?, El 0.5.
Ahora, comprueba tus respuestas.
| Participante | Dado 1 | Dado 2 | ¿Qué cantidad es más grande? |
Para comprobar tus resultados, necesitas dos cintas métricas. Empieza con los resultados de la primera fila.
Dobla en 4 partes iguales una de las cintas y observa de qué tamaño es una de las cuatro partes.
Ahora, dobla la otra cienta en tres partes iguales.
Coloca ambas cintas juntas para comparar su tamaño.
De esta forma habrás podido comprobar que 1/3 es más grande que ¼.
Ahora, ¿por qué se escribió que el 0.05 es más grande que 0.1?
Observa este diagrama. Aquí la barra azul está representando un décimo; que es lo que salió en el segundo dado y la barra roja está representando .05, cinco centésimas. Como puedes darte cuenta 0.1, un décimo es mayor que 0.05, que cinco centésimos.
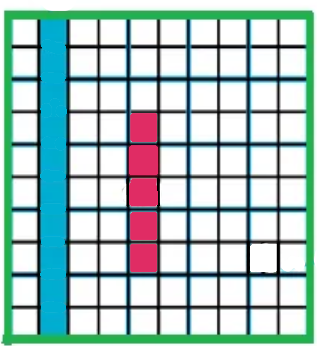
Actividad 2:
Realiza el Desafío Número 35, de tu libro de texto de Desafíos Matemáticos, 6ºgrado, página 72.
A los alumnos de un grupo de sexto grado se les solicitó la medida de su estatura. Los únicos que la sabían la registraron de la siguiente manera: Daniel, 1.4 m; Alicia, un metro con 30 cm; Fernando 1 1/4 m; Mauricio, 1.50 m; Pedro, metro y medio; Sofía 1 1/5 m y Teresa dijo que medía más o menos 1.50 m.
¿Quién es el más bajo de estatura?
Cómo puedes darte cuenta, te están planteando un problema muy interesante, ya tienes los conocimientos que te permitirán llegar a los resultados.
Uno de los caminos que puedes elegir para resolver el problema es identificar los datos con los que vas a trabajar. Dibuja una tabla como la siguiente.
| ALUMNOS | ESTATURA |
| Daniel | 1.4 m |
| Alicia | Un metro con 30 cm |
| Fernando | m |
| Mauricio | 1.50 m |
| Pedro | Metro y medio |
| Sofia | m |
| Teresa | Más o menos 1.50 m |
En la tabla escribe la estatura de las niñas y los niños, exactamente como está en el planteamiento del problema.
Observa los datos de la tabla. Para saber quién es el más bajo de estatura, ¿ sirven los datos como están escritos?. No, porque para comparar las cantidades de las estaturas sería mejor escribirlas todas con número.
En esta tabla, observarás que las cantidades ya están escritas en números.
| ALUMNOS | ESTATURA | ESTATURA |
| Daniel | 1.4 m | 1.4 m |
| Alicia | Un metro con 30 cm | 1.30 m |
| Fernando | 1 ¼ m | m |
| Mauricio | 1.50 m | 1.50 m |
| Pedro | Metro y medio | m |
| Sofia | 1 1/5 m | 1 1/5 |
| Teresa | Más o menos 1.50m | Más o menos m |
Como te puedes dar cuenta, ahora que ya están registrados con números, unas cantidades están escritas en números decimales y otras en fracciones.
¿Qué se puede hacer para comparar las cantidades que tiene decimales con otras que tienen fracciones?
Lo que se tendría que hacer para facilitar la obtención de los resultados es poner todas las cantidades en decimales o en fracciones.
Para empezar has la prueba poniendo todas las cantidades en decimales.
A las cantidades que tienen fracciones, ponles su correspondiente número decimal, como se observa en la siguiente tabla.
| ALUMNOS | ESTATURA | ESTATURA en decimales |
| Daniel | 1.4 m | 1.4 m |
| Alicia | 1.30 m | 1.30 m |
| Fernando | m | |
| Mauricio | 1.50 m | 1.50 m |
| Pedro | m | |
| Sofia | m | |
| Teresa | Más o menos 1.50m | Más o menos 1.50 m |
Si utilizas las cintas métricas vas a identificar que 1¼ de metro es lo mismo que 1.25 m.
| ALUMNOS | ESTATURA | ESTATURA en decimales |
| Daniel | 1.4 m | 1.4 m |
| Alicia | 1.30 m | 1.30 m |
| Fernando | m | 1.25 m |
| Mauricio | 1.50 m | 1.50m |
| Pedro | m | |
| Sofia | m | |
| Teresa | Más o menos 1.50m | Más o menos 1.50m |
¿Por qué = 1.25?
Porque al dividir un metro en cuatro partes, puedes observar que ¼ es lo mismo que 25 cm. Compruébalo con las cintas métricas.
Tienes 1 metro completo y 25 cm del siguiente, por eso coloca el punto entre el 1 y el 25.
Recuerda que, en una cantidad con números decimales, el punto se coloca para separar los enteros de las partes de otro que no está completo.
Entonces la cantidad 1 ½ de metro es igual a 1.50. Escribe la respuesta en la tabla, según corresponda.
Con las cintas métricas comprueba por qué 1 ½ = 1.50.
La cantidad dice 1, eso significa que es un metro completo, obsérvalo con la cinta métrica; pero se agrega ½ más del siguiente metro. Así que dobla a la mitad el metro y puedes ver que la mitad es lo mismo que 50 cm. Por lo tanto, se escribe uno punto 50. De nuevo, coloca el punto para separar los enteros de las partes que son del siguiente entero.
Aplicando este procedimiento, ¿cómo crees que se puede encontrar la estatura de Sofía?
Se puede doblar la cinta métrica en cinco partes iguales, como lo indica el denominador de la fracción y entonces vemos que un quinto es lo mismo que 20 cm. Por lo tanto, la estatura de Sofía es 1.20 m.
Así quedan los datos completos de la tabla, observa y compara los resultados de tu tabla con la siguiente.
| ALUMNOS | ESTATURA | |
| Daniel | 1.4 m | 1.4 m |
| Alicia | 1.30 m | 1.30 m |
| Fernando | 1 ¼ m | 1.25 m |
| Mauricio | 1.50 m | 1.50 m |
| Pedro | 1 ½ m | 1.50 m |
| Sofia | m | 1.20 m |
| Teresa | Más o menos 1.50m | Más o menos 1.50m |
¿A partir de estos resultados puedes saber quién es el o la más bajo de estatura?
¿Quién es el o la de menor estatura?
La más baja de estatura en ese grupo es Sofía, esta es la respuesta a la primera pregunta de nuestro libro.
| ALUMNOS | ESTATURA | |
| Daniel | 1.4 m | 1.4 m |
| Alicia | 1.30 m | 1.30 m |
| Fernando | m | 1.25 m |
| Mauricio | 1.50 m | 1.50m |
| Pedro | m | 1.50 m |
| Sofia | m | 1.20 m |
| Teresa | Más o menos 1.50 m | Más o menos 1.50 m |
Ahora resolverás el inciso b, la segunda pregunta: ¿Quiénes miden lo mismo?, observa la tabla.
Así es, la respuesta es Mauricio y Pedro.
La estatura de estos dos niños es de 1.50 m.
En el inciso c, Teresa no sabe exactamente su estatura, pero al compararse con sus compañeros se da cuenta de que es más alta que Daniel y más baja que Pedro. ¿Cuánto crees que mide?
¿Con estos datos puedes estimar la estatura de Teresa?
Para que lo comprendas mejor, vas a poner en una gráfica, la información que del problema.
Observa bien la imagen. De un lado está la estatura de Daniel, que es de 1.40 y del otro lado está la estatura de Pedro, que es de 1.50. Entre ellos dos está la estatura de Teresa.
Identifica las medidas que estén entre el 1.40 y el 1.50?
1.41; 1.42; 1.43; 1.44; 1.45; 1.46; 1.47; 1.48; 1.49.
Cualquiera de estos números puede ser la estatura de Teresa, ya que todos estos números se encuentran entre la estatura de Daniel y Pedro.
Como puedes darte cuenta, hay nueve opciones como respuesta, para la estatura de Teresa.
Para los números decimales o fraccionarios, es importante tomar en cuenta que, entre un número y otro, siempre van a existir muchos otros números. Lo cual podemos comprobar ampliando los espacios como en la actividad de la regla.
Por ejemplo, al tratar de saber la estatura de Teresa, descubriste nueve números más que pueden representar su estatura y que de momento parece que no existían, pero al analizar la situación los descubriste.
Por eso se dice que entre dos números decimales hay una cantidad infinita de números. Para encontrarlos, lo que se tiene que hacer es ampliar cada espacio entre cualesquiera dos números.
El reto de hoy:
Con las cintas métricas toma las medidas de estatura de algunos integrantes de tu familia y regístralos en una tabla y realiza las comparaciones para identificar quienes son los más altos y los más bajos, utiliza decimales o fracciones, seguramente les parecerá muy interesante.
Si te es posible, consulta otros libros y comparte el tema de hoy con tu familia. Si tienes la fortuna de hablar una lengua indígena aprovecha también este momento para practicarla y platica con tu familia en tu lengua materna.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas







Login to join the discussion