¿Qué pasa con el volumen?

Aprendizaje esperado: calcula el volumen de prismas mediante el conteo de unidades.

Énfasis: usa la relación que hay entre largo, ancho y altura de un prisma con su volumen.

¿Qué vamos a aprender?

Calcularás el volumen de prismas mediante el conteo de unidades para relacionar el largo, ancho y altura de un prisma con su volumen.

¿Qué hacemos?

Continuarás con el estudio del volumen de los cuerpos geométricos, particularmente con los prismas.

Usa tu imaginación y estima el volumen de algunos prismas.

Imagina la construcción de un cuerpo geométrico, usando cubos del mismo tamaño.

Primero coloca de izquierda a derecha tres cubos, luego detrás de cada cubo coloca otras dos filas iguales de cubos.

¿Qué forma tiene?

Parece una cama de cubos, esa cama está formada por nueve cubos.

¿Y qué forma de cuerpo geométrico tiene esta cama de cubos?

Tiene forma de un prisma.

Esta cama tiene forma de un prisma rectangular. ¿Cuál es su volumen? ¿Cuál es el espacio que ocupa?

El de los nueve cubos juntos.

Esta cama de cubos, ¿Qué dimensiones tiene? ¿Cuántos cubos mide de largo? ¿Cuántos mide de ancho y cuántos de alto?

Así como está acomodado, tiene tres de largo, tres de ancho y uno de alto.

Seguramente, el prisma rectangular que imaginaste corresponde con el que aparece en la siguiente imagen, observa.

¿Cuál será el volumen de este prisma que tiene cubierta una parte de su cuerpo?

Observa con atención, recuerda que una manera de obtener el volumen de un prisma es contando uno por uno el número de cubos que lo conforman, pero también considerando sus dimensiones: largo, ancho y alto.

Considera cuántos cubos tiene de largo, cuántos de alto y cuántos de fondo.

¿Cuántos cubos forman ese prisma?

De frente hay dos cubos, desde esta imagen se observa que, hacia la parte de atrás, tiene dos cubos. También se aprecia que, desde su base hasta la parte de arriba, hay 4 cubos.

Entonces con lo que observas puedes proponer que es un prisma que tiene una base formada por 2 cubos en el ancho, 2 en el largo y 4 de altura, son cuatro niveles, entonces, ¿Su volumen podría ser?

Su volumen es de 16 cubos.

¿Cómo se puede comprobar?

Observa la imagen que muestra el prisma ya destapado, para que compruebes que su volumen es de 16 cubos.

Como puedes apreciar, el prisma tiene 16 cubos iguales.

Ahora, busca en tu libro de Desafíos el desafío 69 ¿Qué pasa con el volumen? en la página 128 presta atención a lo que se plantea.

Consigna: En parejas, consideren los siguientes prismas para responder las preguntas. Toma en cuenta que un obstáculo impide ver parte de los prismas.

Analiza lo que solicita el inciso a) ¿Cuál podría tener un volumen equivalente a 18 cubos?

Considera que los cubos azules representarán a los cubos que forman el prisma morado que aparecen en la imagen del libro.

Se usarán los cubos rojos para representar el prisma de color naranja.

¿Cuántos cubos se necesitan para formar cada prisma y de qué manera se puede saber?

Si usas la estrategia de contar los cubos que forman el prisma, tanto en su base como por su altura, puedes decir, en el caso del prisma anaranjado que su base está formada por cuatro cubos y mínimo tiene dos niveles, entonces estará formado por ocho cubos.

¿Y cómo está formado el prisma morado?

En ese caso se observa que hay un nivel con 6 cubos, esto es, 2 x 3 y si son como mínimo dos niveles, igual que en el caso del prisma anaranjado, entonces este prisma morado está formado por doce cubos.

Registra esas dimensiones en una tabla.

Es una tabla como la que se ha estado usando en las otras sesiones para registrar los datos y poder analizar de manera más clara algunas variaciones en las dimensiones de los prismas.

Con los datos registrados, responde: ¿Cuál de estos dos prismas podría tener un volumen equivalente a 18 cubos?

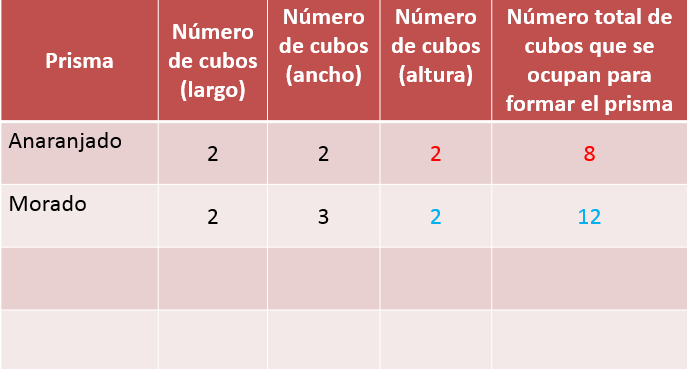
Si se agrega un nivel más de cubos a cada prisma, entonces tendrías que el prisma naranja mediría 2 x 2 x 3 igual a 12 cubos, mientras que, al aumentar un nivel al prisma morado, serían 2 x 3 x 3 esto es 18 cubos.

Ya encontraste las dimensiones de largo, ancho y alto del prisma morado que tendría un volumen de 18 cubos. ¿Crees que para el caso del prisma color naranja exista un número entero de cubos para la base y la altura, cuyo volumen sea 18?

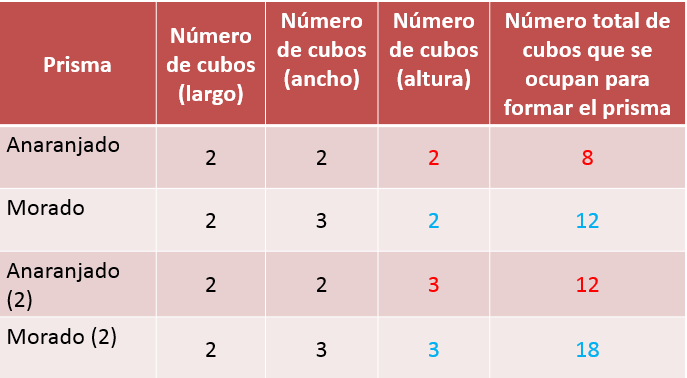
Para investigarlo se podría agregar un nivel más de cubos al prisma anaranjado, de tal manera que ahora sus dimensiones sean 2 x 2 x 4

¿Cuál sería su volumen?

Su volumen es de 16 cubos.

Sigue siendo un volumen menor que 18 cubos.

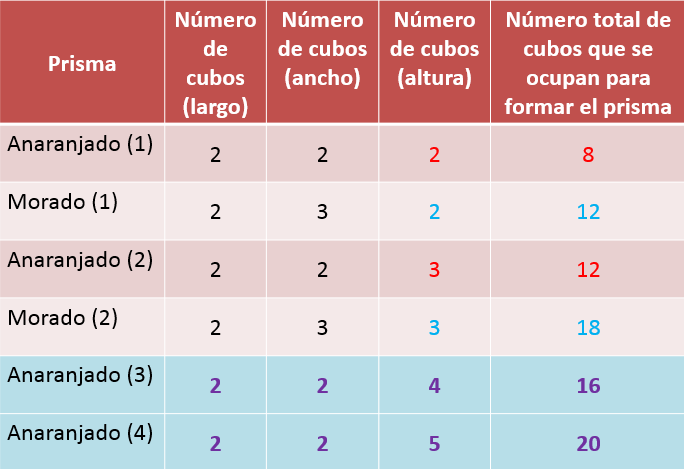
Si se agrega otro nivel de cubos, ahora el prisma mide 2 x 2 x 5 que es igual a 20 cubos.

Ahora el volumen es mayor.

El prisma anaranjado no da 18 de volumen.

En conclusión, el prisma morado si podría tener un volumen de 18 cubos y el anaranjado no.

Revisa lo que te pide el inciso b.

¿Cuál prisma crees que tiene mayor volumen y por qué?

El morado, porque tiene de ancho 3 cubos, mientras que el prisma anaranjado sólo tiene 2 cubos de ancho.

Entonces, ¿Cuáles son las dimensiones de ancho y largo del prisma morado?

3 de largo, 2 de ancho y 4 de altura.

¿Y las dimensiones del prisma anaranjado?

Son 2 de ancho, 2 de largo y también 4 de altura.

Escribe las medidas y ahora calcula su volumen.

Prisma	ancho	largo	alto	volumen
morado	3	2	4
anaranjado	2	2	4

Ahora hay que registrar el volumen.

El prisma morado tiene mayor volumen y la diferencia entre el volumen de ambos prismas es de 8 cubos.

Quedaría de la manera siguiente 3 X 4 X 2 = 24 cubos en el caso del prisma morado. Para el prisma anaranjado sería 2 X 2 X 4 = 16 cubos. ¿Recuerdas que hace un momento también se obtuvo este volumen?

Si duplicas el número de cubos a lo ancho de cada cuerpo, ¿En cuánto se incrementa su volumen?

¿Cómo se puede proceder para contestar la pregunta del inciso c)?

Se haría algo semejante a lo que se hizo en el inciso a) agregar otros niveles de cubos.

Es una buena estrategia tomar como referente los prismas que ya se han armado, entonces, ¿Cuáles serían las nuevas dimensiones del prisma morado si se duplica el número de cubos que tiene de ancho?

De ancho tenía 3 cubos, si se duplica es 6 usando las medidas registradas en la tabla, se tiene que: una posibilidad es que mida 2 de largo, 6 de ancho, y 4 de alto cuyo volumen serían 48 cubos.

De medir 24 cubos al principio, aumentó al doble también su volumen. Observa un ejemplo con el prisma anaranjado.

En este caso quedan 2 de largo, 4 de ancho, porque se duplica 2 y 4 de altura, que fue la que se usó en el inciso b), entonces se tiene que, el volumen es 2 x 4 x 4 esto es 32 cubos, también es el doble del volumen original.

Entonces se tiene que, al duplicar una de las tres dimensiones de los prismas, el volumen del prisma también se duplica.

Ahora hay que comprobar si lo que se supone, es así.

Una manera de hacerlo sería ahora duplicando el largo de cada prisma y conservar las otras dimensiones.

Las respuestas de estos incisos requieren de imaginación espacial, ya que los alumnos pueden imaginar cómo se verá el prisma con la variación de la medida del ancho, pero también requieren de mucha reflexión.

La imaginación y la reflexion ayudan a dar respuestas en este desafío.

Finalmente, el inciso d) pide duplicar la medida del largo y del ancho de cada prisma para saber en cuánto aumenta el volumen original de cada uno. ¿Cuánto estimas que aumente?

Puede ser que aumenta el doble del doble.

Para comenzar a investigarlo, te propongo seguir la estrategia anterior y usar también una tabla donde registres los valores que vas dando a cada dimensión.

Por ejemplo, para el caso del prisma anaranjado se tiene que, el original era 2 x 2 x 4  sí se duplica el ancho y el largo queda 4 x 4 x 4 = 64 cubos.

Recuerda que, para obtener el volumen de un prisma puede realizarse el conteo de cubos iguales que conforman cada nivel o multiplicar las dimensiones de largo, ancho y alto del prisma.

Imagina más prismas y obten su volumen, puedes comprobarlo si utilizas cubitos y armas el prisma.

El reto de hoy:

Revisa los ejercicios que hiciste y elige uno que puedas compartir con algún familiar cercano, explícale como pudiste obtener el volumen de los prismas.

Si te es posible, consulta otros libros o materiales para saber más sobre el tema.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/20/P6DMA.htm

Descarga tu clase dando clic aquí