Proporcionalidad inversa y sus representaciones

Proporcionalidad inversa y sus representaciones

Aprendizaje esperado: analiza y compara situaciones de variación lineal y proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la física y otros contextos.

Énfasis: comparar situaciones de proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica.

¿Qué vamos a aprender?

Continuarás con el estudio de la variación lineal y la proporcionalidad inversa. En esta sesión, abordarás algunas situaciones para analizar sus propiedades a través de la resolución de problemas.

¿Qué hacemos?

Para iniciar, es importante que realices un ejercicio de concentración y memoria.

Cierra los ojos y reflexiona sobre todo lo que has aprendido acerca de la proporcionalidad inversa. Puedes apoyarte respondiendo las siguientes preguntas:

• ¿Qué es la proporcionalidad inversa?
• ¿Cómo es la gráfica de una proporcionalidad inversa?
• ¿Cuál es la expresión algebraica que permite saber el valor de la constante de proporcionalidad inversa?
• ¿Cuál es la expresión algebraica que permite calcular los valores de la variable independiente y de la variable dependiente?

La proporcionalidad inversa es la relación que existe entre los valores de dos magnitudes tales que, si al multiplicar el valor de una de ellas por cualquier número, su valor correspondiente de la otra magnitud queda dividido por el mismo número y viceversa. Es decir, si un valor de una magnitud es dividido por un número, el valor correspondiente de la otra magnitud es multiplicado por el mismo número.

Por ejemplo, en la siguiente tabla se puede observar que al multiplicar el primer valor de la magnitud (largo) por el número 2, se obtiene como resultado 2. Entonces, ¿qué operación se debe realizar al primer valor de la magnitud (ancho) para comprobar que es inversamente proporcional a su valor correspondiente?

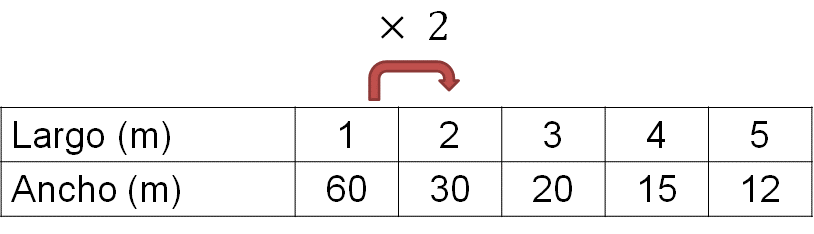
Habrá que dividirlo entre 2. Así se comprueba que las magnitudes de la tabla son inversamente proporcionales.

La gráfica que define una proporcionalidad inversa está representada en el plano cartesiano por una hipérbola. Observa el ejemplo.

En la gráfica puedes ver, para el mismo ejemplo, cómo a medida que aumentan sus valores en el eje “x”, sus valores en el eje “y” disminuyen. También se observa el caso inverso: a medida que los valores en el eje “y” aumentan, los valores en el eje “x” disminuyen. La gráfica que representa una situación de proporcionalidad inversa es una curva llamada hipérbola.

Por otra parte, en una relación de proporcionalidad inversa, la constante de proporcionalidad se representa con la expresión algebraica:

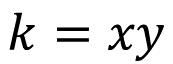
Es decir, “k” es el producto de cada pareja de valores correspondientes de ambas magnitudes “x” y “y”, y el resultado siempre será el mismo, en otras palabras, es constante. Observa el siguiente ejemplo.

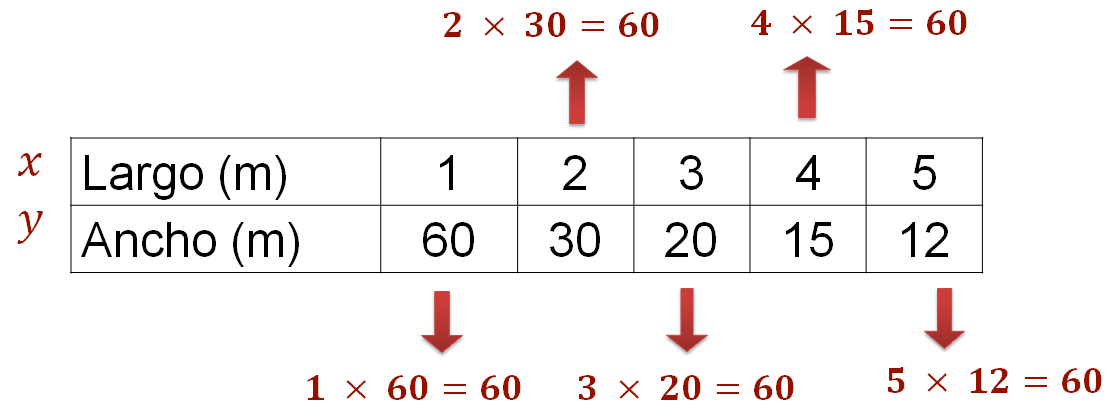
Para saber cómo calcular los valores faltantes en una proporcionalidad inversa, se puede utilizar la expresión algebraica que determina la constante de proporcionalidad y despejar “x” o “y”, según las necesidades del problema.

Para calcular la constante de proporcionalidad “k”:

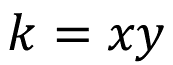
Para calcular la variable “y”:

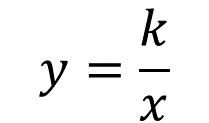
Para calcular la variable “x”:

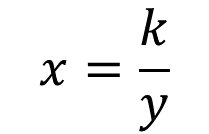
Hasta este momento, has recapitulado todo lo necesario para poder resolver problemas de proporcionalidad inversa. Así que manos a la obra. Analiza y resuelve la siguiente situación.

Situación-problema: velocidad-tiempo de un auto

Se quiere saber los diferentes tiempos y las diferentes velocidades a las que un auto debe circular para recorrer una distancia fija de 50 kilómetros.

Observa y analiza la tabla. Calcula los valores faltantes de la variable dependiente y de la variable independiente. También elabora una gráfica que represente la situación.

En la tabla se puede observar que faltan valores para el tiempo, es decir, la variable independiente “x”. También faltan valores para la velocidad, es decir, la variable dependiente “y”. Para calcular los valores faltantes se puede hacer uso de las expresiones algebraicas anteriores. Realiza los cálculos.

Es conveniente definir cuál es la expresión algebraica para calcular el tiempo y cuál es la expresión algebraica para calcular la velocidad. Toma un momento para pensar y decidir.

Seguramente identificaste que, para calcular el tiempo o la velocidad, se necesita el valor de “k”, es decir, de la constante de proporcionalidad inversa. ¿Ya sabes cuál es su valor?

Es 50, porque el problema dice que el auto deberá recorrer una distancia fija, además, en la tabla se puede comprobar que al multiplicar las parejas de valores correspondientes que están completas, el resultado es 50

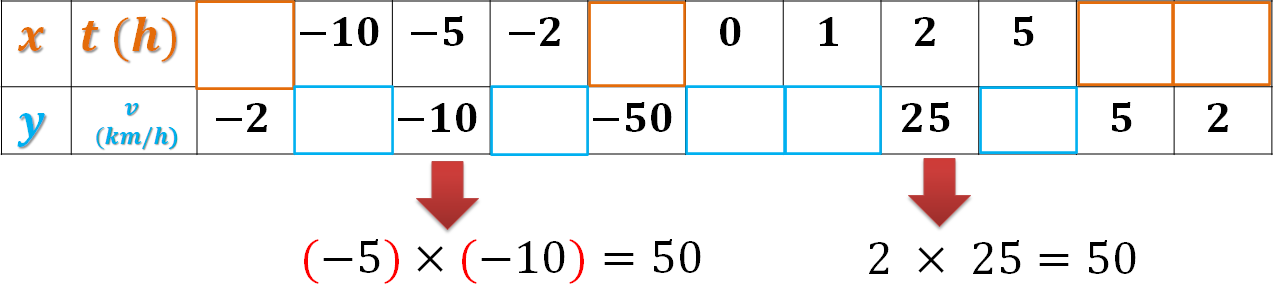
Ya cuentas con los datos para realizar los cálculos.

El primer valor para calcular corresponde al tiempo cuando la velocidad es 2 negativo, por lo que se puede usar la expresión algebraica:

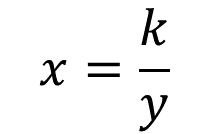
Es decir, el tiempo es igual a la constante de proporcionalidad inversa entre la velocidad. Se sustituyen los valores

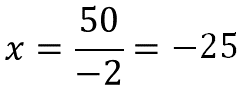
El resultado es 25 negativo y se registra en la tabla.

Ahora se calcula el valor correspondiente a la velocidad cuando el tiempo es 10 negativo. Se usa la expresión algebraica:

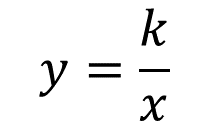
Es decir, la velocidad es igual a la constante de proporcionalidad inversa entre el tiempo. Se sustituyen los valores y la velocidad es igual a 50 entre 10 negativo.

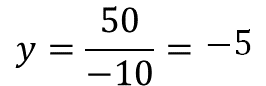
El resultado es 5 negativo.

Después se aplica el mismo procedimiento para calcular el valor correspondiente a la velocidad cuando el tiempo es 2 negativo. Se sustituyen valores y se resuelven las operaciones:

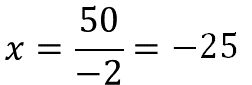
El resultado es 25 negativo.

Para calcular el valor correspondiente al tiempo cuando la velocidad es 50 negativo, se sustituyen los valores y se realizan los cálculos

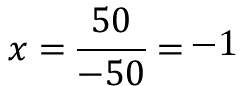
El resultado es 1 negativo cuando la velocidad es 50 negativo.

Se ha calculado una parte de los datos, pero ¿habrá alguna otra forma de saber los valores faltantes sin realizar todo ese procedimiento?

Otra forma de conocer los valores faltantes es a través de la constante de proporcionalidad inversa. Se sabe que, si se multiplican los valores correspondientes del tiempo y la velocidad, el resultado siempre debe ser 50. Entonces, para calcular los valores que faltan, se puede hacer mentalmente, buscando un número que, multiplicado por el valor conocido, dé como resultado 50. Continúa con los datos faltantes.

De acuerdo con la tabla, el tiempo vale 1, entonces, para calcular la velocidad en ese momento, se determina un número que multiplicado por 1 dé como resultado 50. El resultado es 50. Para calcular la velocidad cuando el tiempo es 5, se determina un número que multiplicado por 5 sea 50. El número es 10. El valor del tiempo cuando la velocidad es 5, es 10. El valor del tiempo cuando la velocidad es 2, es 25.

Aún nos falta calcular el valor de la velocidad cuando el tiempo es cero. Se puede aplicar la fórmula o determinar un número que multiplicado por cero sea 50

Toma unos instantes para hacer los cálculos y reflexiona:

¿Cuál fue el resultado?

¿Realmente “x”, es decir, el tiempo puede valer cero?, ¿por qué?

¿Qué significa que el tiempo valga cero?

¿Son necesarios los números negativos en el contexto de este problema?, ¿por qué?

Piensa unos instantes para responder cada una de estas preguntas.

Ya sea que hayas dividido 50 entre cero a mano, en calculadora, en el celular u hoja de cálculo, no fue posible determinar un resultado; lo mismo pasa si intentas buscar un número que multiplicado por cero de como resultado 50. Simplemente no es posible calcular el resultado, esto se debe a que la división por cero no está definida y no es posible interpretarla a través de la aritmética.

Entonces ¿realmente “x”, es decir, el tiempo, puede valer cero? Después de haber realizado los cálculos, la respuesta lógica es no, pero ¿qué significa que el tiempo valga cero? Una interpretación es que no se requiere tiempo para recorrer esa distancia y eso es imposible físicamente.

Por último, ¿realmente son necesarios los números negativos en este problema?, ¿por qué? La respuesta es no, porque en el contexto de este problema no existen velocidades ni tiempos negativos. Por ejemplo, no existe un auto que viaje a -30 kilómetros por hora, o que tarde en llegar a alguna parte -2 horas negativas. Analizar el contexto de un problema permite tomar decisiones sobre los datos a utilizar para su resolución.

Observa cómo queda la tabla:

Es momento de elaborar la gráfica. Y con la información anterior, te puedes dar cuenta de que no es necesario utilizar los valores negativos, porque el contexto del problema limita su uso.

Lo primero será trazar el cuadrante del plano cartesiano; después, escribir los valores de la variable independiente tiempo y de la variable dependiente velocidad; determinando la escala en cada eje, en este caso de 5 en 5 para el eje “y” y de 2 en 2 para el eje “x”

Después se marca con un punto dónde se ubica en el plano cartesiano cada pareja de valores correspondientes. Una vez marcados todos, se traza la línea que define la gráfica. Queda de la siguiente manera:

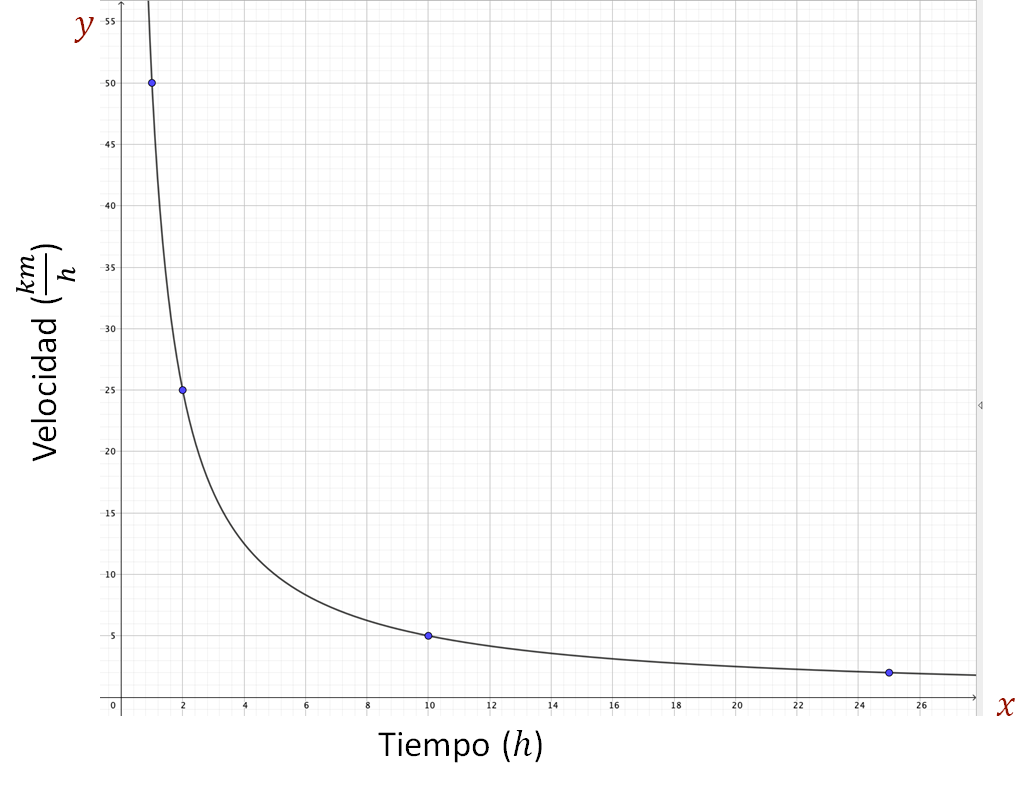
Ahora, ¿qué se puede decir acerca de la gráfica?

Se puede ver que, a mayor tiempo, menor velocidad y viceversa.

Finalmente, reflexiona:

¿Qué pasa con el cero?

En el recorrido de la línea, ¿en algún momento pasa por el cero?

¿A qué se supone que se deba?

Toma un momento para pensarlo, y en tu cuaderno escribe una conclusión al respecto.

Ahora fortalecerás lo que has aprendido sobre gráficas haciendo la interpretación y comparación de un par de ellas.

Las siguientes gráficas y expresiones algebraicas representan la proporcionalidad inversa. Analízalas y encuentra puntos en común o de diferencia.

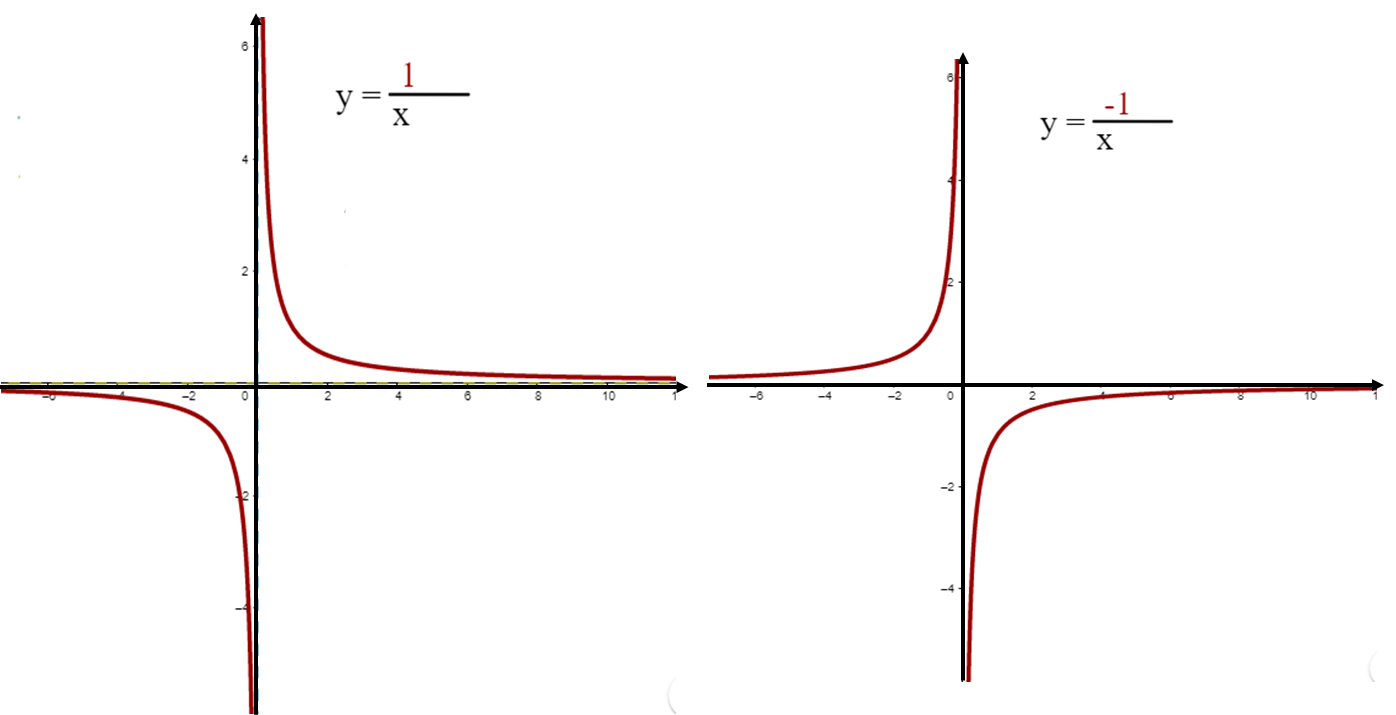
Se pueden ver dos gráficas que tienen los mismos valores en el eje “x” y en el eje “y”. También que en ambas aparecen líneas curvas que definen la gráfica, las cuales, se sabe, se llaman hipérbolas. Otra cosa que se nota es una expresión algebraica en cada gráfica, que como seguramente ya identificaste, se trata de la expresión que permite calcular los valores de la variable dependiente. En el denominador aparece “x”, es decir, los valores que puede tomar la variable independiente, mientras que en el numerador aparece el número 1. Pero en una expresión el número 1 es positivo y en la otra es negativo.

¿Qué valor representan el 1 y 1 negativo en cada expresión algebraica?

¿Cómo influye en la gráfica el signo que pueda tomar la constante de proporcionalidad inversa?

¿Qué tiene que ver el cero con todo esto?

Para responder estas preguntas, analiza los siguientes ejemplos.

Para responder la primera pregunta, se necesita comparar las expresiones algebraicas que aparecen en las gráficas con la expresión algebraica que se usa para calcular los valores que puede tomar la variable dependiente, es decir, “y”.

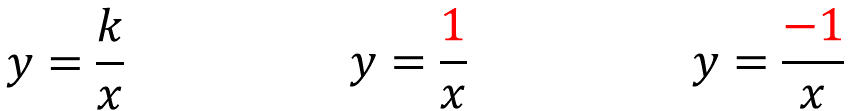
Como puedes observar, el número 1 y el 1 negativo se encuentran situados en el mismo lugar donde aparece la letra “k”. En otras palabras, el numerador; en esa forma de la expresión algebraica de la proporcionalidad inversa, siempre será el valor que representa la constante de proporcionalidad inversa.

Para responder la segunda pregunta: ¿cómo influye en la gráfica el signo que pueda tomar la constante de proporcionalidad inversa?, es necesario analizar varias gráficas simultáneamente, en donde la constante de proporcionalidad inversa represente valores negativos y positivos. Observa los ejemplos.

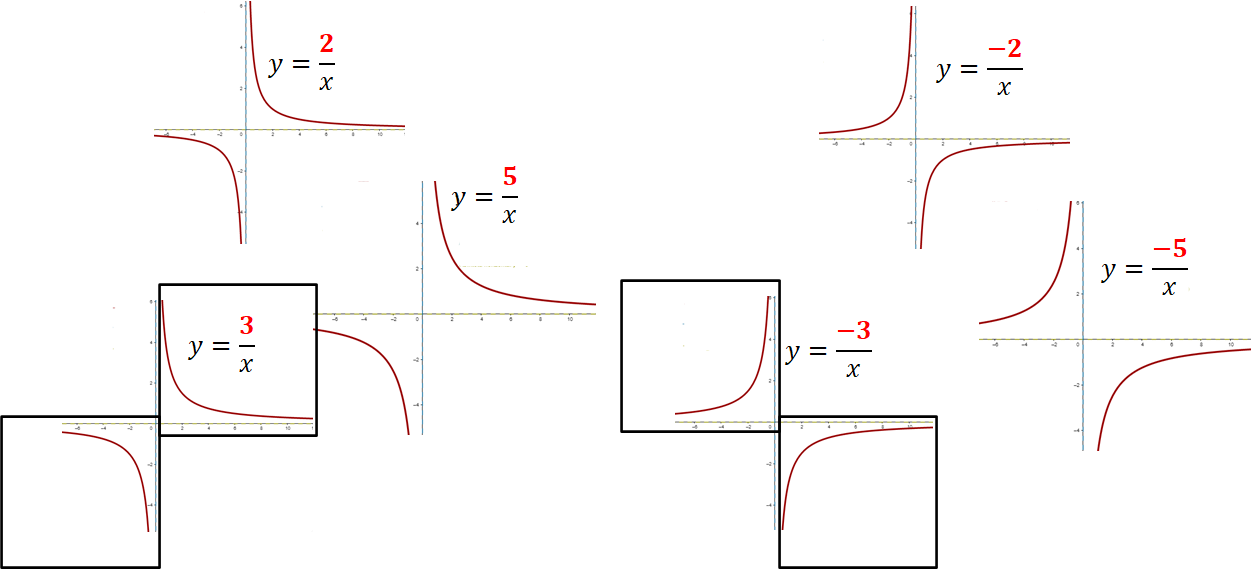
Hay seis gráficas de funciones de proporcionalidad inversa, tres de ellas con constante de proporcionalidad negativa y otras tres con constante de proporcionalidad positiva. ¿Qué puedes decir sobre el lugar que ocupan las líneas en cada gráfica y cómo se relaciona con el signo de la constante de proporcionalidad?

Cuando la constante de proporcionalidad inversa tiene valores negativos, la línea que define la gráfica siempre se encontrará en la parte superior izquierda si los valores de “x” son negativos, y en la parte inferior derecha si los valores de “x” son positivos; es decir, en los cuadrantes dos y cuatro de un plano cartesiano, respectivamente.

Por otro lado, cuando la constante de proporcionalidad inversa tiene valores positivos, la línea que define la gráfica siempre se encontrará en la parte superior derecha si los valores de “x” son positivos, y en la parte inferior izquierda si los valores de “x” son negativos. Es decir, en los cuadrantes uno y tres de un plano cartesiano.

Para responder la pregunta: ¿qué tiene que ver el cero con todo esto? Se sabe que, en las gráficas de proporcionalidad inversa, la línea que las define no pasa nunca por el cero, entonces, el cero será el punto de referencia y de partida para el análisis.

Las gráficas de proporcionalidad inversa pueden crecer o decrecer y que esto suceda depende directamente del signo de la constante de proporcionalidad.

Si la constante de proporcionalidad es menor que cero (negativo), entonces la gráfica es creciente. Pero ¿esto qué quiere decir? Que una gráfica de proporcionalidad inversa sea creciente significa que al aumentar la variable independiente “x”, aumenta también la variable dependiente “y”

Por otro lado, en una relación de proporcionalidad inversa, siempre que la constante de proporcionalidad sea mayor que cero (positivo), la gráfica siempre será decreciente, entonces, al aumentar la variable independiente “x”, la variable dependiente “y” disminuirá.

Hasta ahora, has resuelto problemas que involucran funciones de proporcionalidad inversa, también has analizado algunas de sus propiedades. Por lo tanto, se puede concluir que:

• En una relación de proporcionalidad inversa, su gráfica es creciente si la constante de proporcionalidad es menor que cero o negativa, y es decreciente si la constante de proporcionalidad es mayor que cero o positiva.
• La gráfica de una proporcionalidad inversa es creciente o decreciente a través del lugar en donde la línea que define la gráfica se ubique. Si la línea se ubica en los cuadrantes 1 y 3, la gráfica es decreciente, y si se ubica en los cuadrantes 2 y 4, la gráfica es creciente.
• La línea que define la gráfica de una relación de proporcionalidad inversa puede estar muy cerca del cero, pero jamás pasará por él.

Has finalizado esta sesión, dedicada al análisis de las propiedades de la proporcionalidad inversa a través de la resolución de problemas.

Recuerda que este es un material de apoyo, y para complementar lo estudiado puedes consultar otras fuentes, como tu libro de texto de Matemáticas de segundo grado.

El reto de hoy:

Ahora que ya conoces más sobre las propiedades de la proporcionalidad inversa, resuelve el siguiente problema.

El producto de dos números es 24. ¿Cuáles son los valores que pueden tomar estos números?

Si se elabora la gráfica de cada pareja de los números obtenidos, ¿la gráfica es creciente o decreciente?

Argumenta tu respuesta.

Analiza la situación y escribe en tu cuaderno un breve procedimiento sobre cómo resolverlo.

Para resolver este problema se deben formar parejas de números cuyo producto siempre sea 24, es decir, el 24 es un valor constante y representa el valor de la constante de proporcionalidad.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/