Proporcionalidad inversa IV

Proporcionalidad inversa IV

Aprendizaje esperado: analiza y compara situaciones de variación lineal y proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la física y otros contextos.

Énfasis: interpretar y resolver problemas que se modelan con este tipo de variación, incluyendo fenómenos de Física II.

¿Qué vamos a aprender?

En esta sesión interpretarás y resolverás problemas de proporcionalidad inversa, incluyendo fenómenos de la física.

¿Qué hacemos?

Antes de comenzar a analizar y resolver, es trascendental recuperar algunos conceptos clave sobre la proporcionalidad inversa, ya que al tenerlos presentes será más práctico saber qué hacer en cada situación.

¿Qué es la proporcionalidad inversa?

La proporcionalidad inversa es la relación que existe entre los valores de dos magnitudes tales que, si al multiplicar el valor de una de ellas por cualquier número, el valor correspondiente de la otra magnitud, queda dividido por el mismo número y viceversa. Es decir, si el valor de una magnitud es dividido por un número, el valor correspondiente de la otra magnitud es multiplicado por el mismo número.

Piensa sobre cuál es el nombre y la forma de la curva que define una gráfica de proporcionalidad inversa. Toma un momento y en tu cuaderno dibuja una gráfica representativa de la proporcionalidad inversa. Después compara tu gráfica con la que se muestra en la siguiente imagen e identifica las diferencias si las hubiera y corrige de ser necesario.

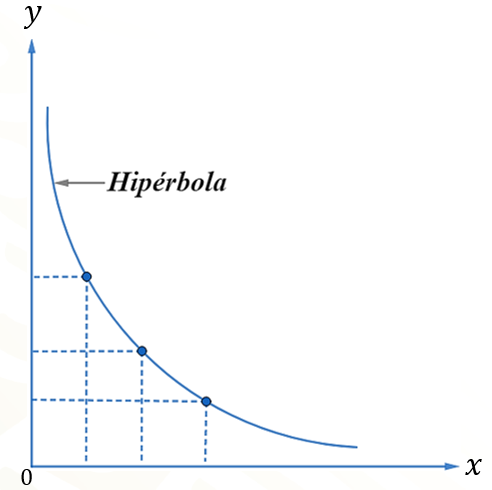
Como puedes ver, la gráfica de la proporcionalidad inversa es una línea curva llamada hipérbola y dependiendo del valor de la constante de proporcionalidad, será su ubicación en el plano cartesiano.

Toda relación de proporcionalidad tiene una constante de proporcionalidad. En el caso de la proporcionalidad inversa, la constante de proporcionalidad está definida por el producto de los valores correspondientes de las magnitudes relacionadas y se representa con la letra “k”.

Por ejemplo, en la siguiente tabla se muestran valores que relacionan el ancho y el largo de un rectángulo cuya área es de 60 centímetros cuadrados. Como puedes apreciar, el producto de cada pareja de datos es 60 y ese valor siempre será constante. La fórmula para calcular la constante de proporcionalidad inversa está dada por “k” es igual a “x” por “y”.

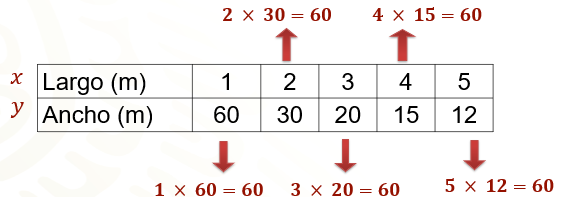
En la resolución de actividades que implican proporcionalidad inversa, generalmente se solicita calcular valores faltantes que corresponden a la variable independiente “x” o en su defecto, a la variable dependiente “y”.

¿Cuáles son las fórmulas que les permiten calcular los valores faltantes de cualquier variable, en la proporcionalidad inversa?

Si te piden calcular el valor de la variable dependiente, podrás usar la fórmula:

Por otro lado, si tienes que calcular el valor de la variable independiente, podrás usar la fórmula:

Con las ideas que has recuperado, ya cuentas con todo lo necesario para poder identificar, analizar y resolver situaciones de proporcionalidad inversa en contextos no necesariamente matemáticos. Las matemáticas son útiles para describir y comprender todo lo que te rodea, por ejemplo, cosas que parecen tan comunes o naturales como distinguir los colores.

¿Sabías que la manera en la que distinguimos los colores está relacionada con la proporcionalidad inversa?

Para comprenderlo un poco, se tiene que hablar de las ondas electromagnéticas, por ejemplo, de la amplitud, la longitud de onda y la frecuencia.

Algunas ondas electromagnéticas, oscilan y se propagan en el espacio, y a grandes rasgos, la frecuencia describe el número de ondas completas que pasan por un punto dado del espacio en un segundo. La unidad de medida para la frecuencia es el hertz y se simboliza con las letras “hz”; se escribe como 1 entre “s”, o bien como “s” elevado a la potencia negativo 1. Se utiliza la “s” porque los hertz son una medida relacionada con los segundos, de hecho, se puede leer “por segundo”.

La longitud de onda (λ) y la frecuencia (f) son inversamente proporcionales, es decir, mientras más corta sea la longitud de onda de una radiación electromagnética, más alta será la frecuencia y viceversa.

Esta relación está dada por la expresión v="λf", en este caso como hablamos de las ondas electromagnéticas, relacionadas a los colores, éstas tienen una velocidad aproximada a la velocidad de la luz y su fórmula es 𝒄="λf".

La letra griega “lambda” (λ) Representa la longitud de la onda y se mide en metros."

Mientras que la letra “f” representa a la frecuencia en hertz.

Al ser una relación inversamente proporcional, el producto de estas dos magnitudes es un valor constante, en este caso simbolizado por la letra “c” que representa a la velocidad de la luz, aproximadamente 3 × 10^8 m/s.

Pues bien, gracias a las ondas electromagnéticas, la longitud de onda y la frecuencia, entre otros factores biológicos, es que podemos distinguir los colores. Las ondas electromagnéticas se pueden clasificar de acuerdo con sus longitudes y frecuencias. A esa clasificación se le conoce como el espectro electromagnético.

De todo el espectro electromagnético, lo visible al ojo humano es una pequeña parte de todas las clases de radiación electromagnética que existen en nuestro universo. Se trata de la zona más estrecha del espectro con frecuencias que oscilan entre 3 por 10 elevado a la 14 hertz y 7 por 10 elevado a la 14 hertz. Es lo que comúnmente conocemos como luz y son ondas electromagnéticas capaces de ser captadas por nuestros ojos. Pues en ese pequeño intervalo, se encuentran los colores.

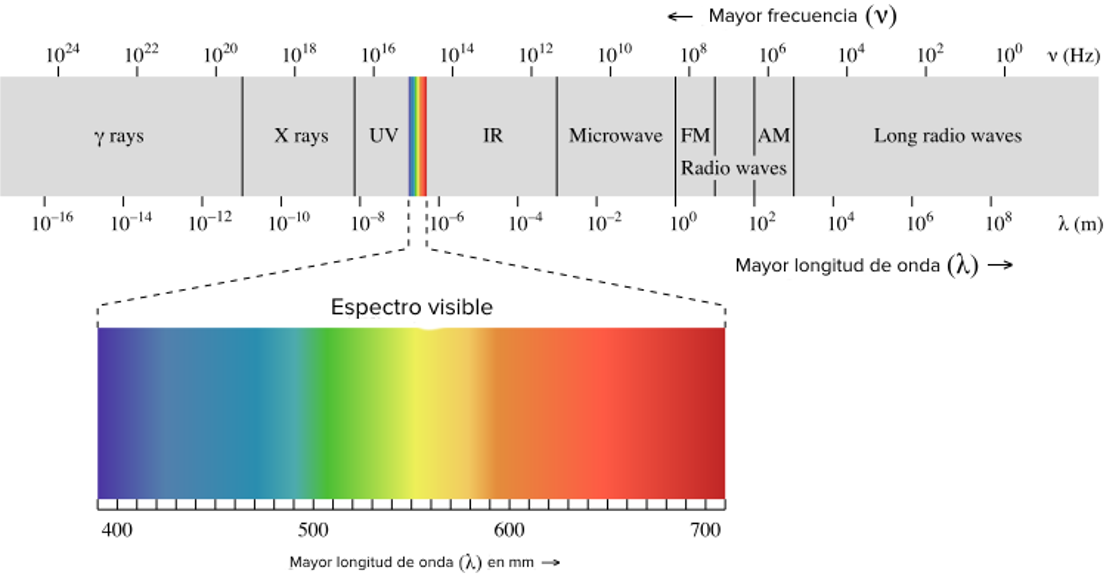
Si se toma como referencia la gráfica mostrada del espectro electromagnético se podría decir que toda la energía que se ubica a la derecha del espectro visible son energías con menores frecuencias y mayores en longitud de onda, entre las que se encuentran los rayos infrarrojos, las microondas, señales de radio y de televisión, entre otras, que no representan aparentemente riesgos a la salud.

A la izquierda del espectro visible están los rayos ultravioletas, los rayos “X”, los rayos gama, entre otros, que son considerados dañinos para los organismos vivos, es por esta razón que solemos usar medidas de protección para evitar daños en la salud cuando estamos expuestos a ellos.

Como puedes notar, la manera en la que distinguimos los colores es una combinación de factores físicos y bilógicos y es posible saber con precisión, a través de cálculos matemáticos, si una energía corresponde al espectro visible o no, además, se puede saber si esa energía puede o no poner en riesgo nuestra salud. Por ejemplo:

Una onda particular de la radiación electromagnética tiene una frecuencia de 1.5×10^14 𝐻𝑧. ¿Cuál es su longitud de onda? ¿Es visible para el ser humano? Exponerse a esa onda de radiación electromagnética particular, ¿podría poner en riesgo su salud?

Utiliza la fórmula anterior para elaborar tus planteamientos y responder a las preguntas.

Una manera de responder estas preguntas es comenzar con la fórmula anterior, la velocidad de la onda es igual a la longitud de la onda por la frecuencia.

𝒄="λf"

La situación requiere de conocer la longitud de la onda, por lo tanto, debes despejar esa variable de la expresión original. Aplicando las propiedades de la igualdad obtenemos la expresión.

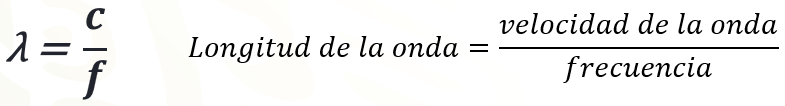
En otras palabras, la longitud de onda es igual al cociente de la velocidad de onda entre la frecuencia.

Una vez despejada la variable que se requiere calcular, lo siguiente es sustituir los valores que se conocen.

Se conoce el valor de la frecuencia de 1.5×10^14 𝐻𝑧. También se conoce la velocidad de la onda, ya que, como se dijo, es igual a la velocidad de la luz, aproximadamente 3 × 10^8 m/s; entonces se plantean las operaciones y se obtiene lo siguiente.

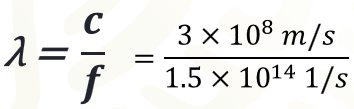
Se resuelve la división y el cociente es igual a:

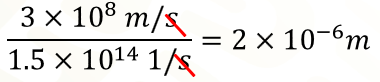
Ten presente que en divisiones de potencias con la misma base se resuelve la división entre coeficientes, la base se conserva y el exponente resultante será la diferencia de los exponentes.

Respecto a las unidades de medida, se simplifican los segundos como consecuencia de estar en el numerador y denominador.

El resultado con su unidad de medida es:

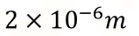
Con el resultado obtenido ya es posible responder a las preguntas planteadas.

La longitud de onda ya está dada por el resultado de los cálculos realizados. ¿Qué estrategia sugieres para saber si esta onda es visible para el ser humano?

Para responder esta pregunta, es posible recurrir al esquema que muestra el espectro electromagnético y ubicar ahí el resultado obtenido, de esa manera puedes determinar si la onda particular de la radiación electromagnética es visible o no.

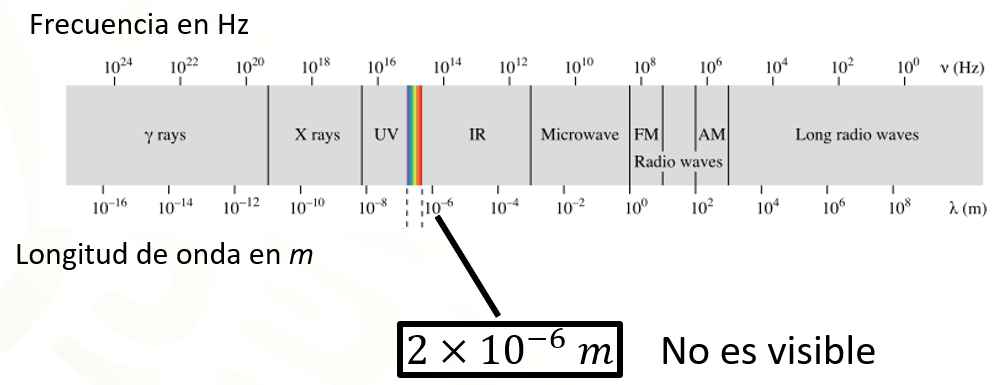
El esquema muestra en la parte superior las frecuencias medidas en hertz y en la parte inferior la longitud de la onda expresada en metros.

Piensa en el esquema como una tabla de valores; si se hace una lectura del esquema de izquierda a derecha, se puede observar que conforme disminuye la frecuencia, la longitud de la onda aumenta. Sucede lo inverso si se hace una lectura del esquema de derecha a izquierda, es decir, conforme aumenta la frecuencia, la longitud de la onda disminuye.

El resultado que se calculó está expresado en base 10 y exponente negativo 6. El valor que se calculó corresponde a la longitud de la onda, entonces se debe ubicar el resultado en esa unidad de medida.

Es posible hacer una aproximación de su ubicación en el espectro electromagnético a través del exponente del resultado, en este caso, 6 negativo. Al ubicar el valor en el esquema, se puede ver que no está dentro del intervalo correspondiente a lo visible por el ojo humano y con esto hemos respondido la segunda pregunta.

Aún falta por responder si esa onda de radiación electromagnética puede ser dañina para la salud.

Párrafos atrás se mencionó sobre la ubicación de las ondas que son dañinas para la salud en función de lo que es visible; si estaba a la derecha del espectro visible no podía perjudicar la salud de los seres vivos. Como pudiste observar, esta particular onda, se ubica a la derecha del espectro visible, por lo tanto, se puede concluir que no es dañina para la salud de los seres vivos.

Piensa en cuáles situaciones se puede usar la información sobre el espectro electromagnético y escribe en tu cuaderno un par de ideas sobre ello.

¿Alguna vez has dialogado con alguien sobre si el color que perciben es verde o azul, naranja o amarillo?, ¿te imaginas poder definir un color a través de la proporcionalidad inversa? Pues esto es posible gracias al espectro electromagnético.

El espectro visible sólo es una pequeña parte de la totalidad del espectro y en esa pequeña parte se encuentran las longitudes de onda y frecuencias que pueden definir con gran precisión los colores, por ejemplo.

Una onda de radiación electromagnética particular tiene una frecuencia de 0.7×10^15 𝐻𝑧. Si la velocidad de la onda se considera de 3×10^8 𝑚/𝑠 ¿Cuál es su longitud de onda? ¿A qué color corresponde la onda de radiación electromagnética?

La fórmula para calcular la longitud de onda cuando la despejaron de la expresión que representa a la constante de proporcionalidad. La fórmula que se obtiene es:

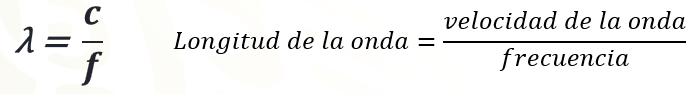
Ya que hayas escrito la fórmula, sustituye los valores de las variables conocidas, en este caso se conoce el valor de la velocidad de onda y el valor de la frecuencia. Al realizar la sustitución se tiene que la longitud de onda es igual a:

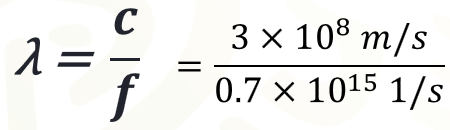
Se resuelve la división indicada y el cociente es aproximadamente:

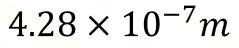
Recuerda que en divisiones de potencias con la misma base se resuelve la división entre coeficientes, la base se conserva y se restan los exponentes.

Recuerda que se deben simplificar las unidades de medida. En este caso se simplifican los segundos porque se encuentran tanto en el numerador como en el denominador, quedando como resultado, la unidad de medida, metros.

Ya obtuviste el resultado numérico de la longitud de onda, solamente falta determinar al color que corresponde; para ello, te puedes ayudar con la siguiente tabla.

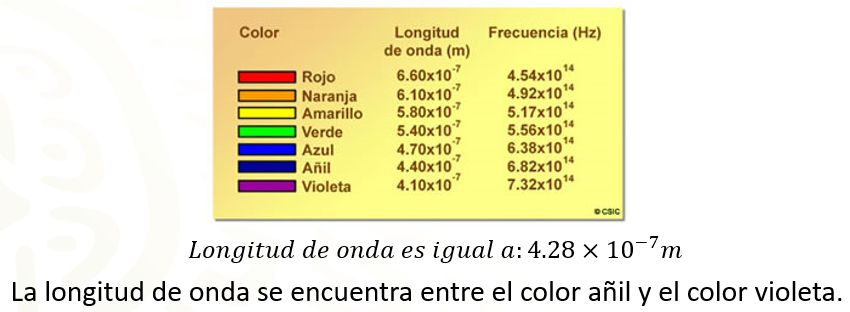
Antes de determinar a qué color corresponde la longitud de onda calculada, haz un análisis de la tabla. ¿Qué observas? ¿Puedes distinguir la proporcionalidad inversa en los datos de la tabla?

En la primera columna de la tabla se pueden observar los colores que se perciben a través del espectro electromagnético; en la segunda columna se encuentra la medida de la longitud de onda expresada en notación científica y en metros, por último, en la tercera columna, aparece la frecuencia expresada en hertz que corresponde a cada longitud de onda y color respectivamente.

Observa a detalle los coeficientes de la longitud de onda como los coeficientes de la frecuencia. ¿Qué puedes decir al respecto?

Si lees los datos de arriba hacia abajo, los coeficientes de la longitud de onda disminuyen y van desde 6 punto 60 por diez a la menos 7 m, que corresponde al color rojo, al 4 punto 10 por diez a la menos 7 m, que corresponde al color violeta. Por otro lado, si haces la misma lectura, pero en la frecuencia, notarás que los valores de los coeficientes van aumentando.

Lo anterior significa que la longitud de onda de una radiación electromagnética es inversamente proporcional a la frecuencia, es decir, a menor longitud de onda, mayor será la frecuencia en la misma proporción y viceversa.

Ya hiciste un breve análisis de los datos de la tabla, es momento de responder la pregunta sobre ¿a qué color corresponde la onda de radiación electromagnética?

El valor de la longitud de onda calculado fue de 4.28×10^⁻⁷ 𝑚. Al ubicar ese valor en la columna de datos correspondientes, puedes observar que el dato calculado se encuentra entre los coeficientes 4.10 y 4.40, es decir, un color intermedio entre el color añil y violeta, es decir entre morado y violeta.

La proporcionalidad inversa también está relacionada con la manera en la que se emite el sonido en los instrumentos de cuerda, como por ejemplo el arpa, el violín, la guitarra, por mencionar sólo algunos.

La frecuencia del sonido producido por una cuerda es inversamente proporcional a la longitud de ésta.

Esto quiere decir que a mayor frecuencia menor es la longitud de la cuerda y viceversa. En otras palabras, las cuerdas cortas corresponden a frecuencias altas y las cuerdas largas corresponden a frecuencias bajas.

Lee con mucha atención el siguiente problema y piensa en una estrategia para resolverlo.

La longitud (l) de una cuerda de violín varía inversamente proporcional con la frecuencia (f) de sus vibraciones. Una cuerda de violín de 32 centímetros de largo vibra a una frecuencia de 450 ciclos por segundo (Hz). Calcula la frecuencia de una cuerda de violín de 24 centímetros.

Una manera de resolver el reto es analizando la información que ofrece el problema. El problema dice que la longitud, “l”, varía inversamente proporcional con la frecuencia, “f”. ¿Qué interpretación le das a este enunciado? ¿Qué representa matemáticamente esta relación?

Al ser una relación de proporcionalidad inversa, el enunciado se puede interpretar como, mientras más larga sea la cuerda, menor es su frecuencia; por otro lado, mientras más corta sea la cuerda, mayor será su frecuencia.

Matemáticamente la relación longitud de cuerda por la frecuencia, representa a la constante de proporcionalidad inversa representada por la siguiente expresión.

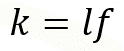
Al sustituir los datos conocidos, se tiene la siguiente expresión:

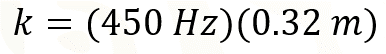
Resolviendo las operaciones, el producto es igual a:

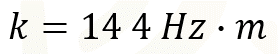
El problema solicita calcular la frecuencia de una cuerda de violín de 24 centímetros de longitud, es decir, la frecuencia será la incógnita por conocer. Por lo tanto, de la fórmula de la constante de proporcionalidad se deberá despejar a la variable “f”.

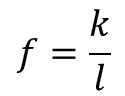
Es decir, la frecuencia es igual al cociente de la constante de proporcionalidad entre la longitud de la cuerda.

Con estos datos, ya es posible calcular la frecuencia de la cuerda. Para ello sustituye los valores conocidos en la fórmula y realiza las operaciones indicadas.

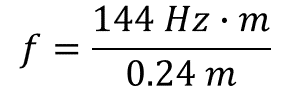
Se realiza el análisis dimensional y se simplifica la unidad de medida “metros” que aparece tanto en el numerador como en el denominador de la expresión. El resultado con su unidad de medida correspondiente es:

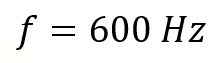
Como seguramente ya notaste, al disminuir la longitud de la cuerda de 32 centímetros a 24 centímetros, la frecuencia aumentó de 450 hertz a 600 hertz, esto quiere decir que efectivamente hay una relación de proporcionalidad inversa entre la longitud de una cuerda y la frecuencia de sus vibraciones.

Pero ¿para qué es útil saber la frecuencia de las vibraciones de una cuerda según su longitud?

Piénsalo un momento y escribe en tu cuaderno una conclusión al respecto.

Así como sucede con los colores, en el sonido, cada nota tiene sus intervalos de frecuencia y también existen intervalos de tonos. Las frecuencias bajas entre 16 hertz y 256 hertz corresponden a los tonos graves; las frecuencias medias entre 256 hertz y

2 000 hertz corresponden a los tonos medios, por último, las frecuencias altas entre 2 000 hertz y más de 16 000 hertz corresponden a los tonos agudos.

La frecuencia calculada corresponde a los tonos medios, ya que la frecuencia de las vibraciones de la cuerda de violín de 24 centímetros es de 600 hertz y se ubica en este intervalo de tonos.

Recuerda que este es un material de apoyo, y para complementar lo estudiado puedes consultar otras fuentes, como tu libro de texto de Matemáticas y de Ciencias de segundo grado.

El reto de hoy:

Te retamos a que escribas algunas aplicaciones en las que se puede usar esta relación de proporcionalidad inversa que acabas de conocer. Después intercambia ideas a distancia con tus compañeras y compañeros.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html