Proporcionalidad inversa
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:22
Aprendizaje esperado: l ee y representa, gráfica y algebraicamente, relaciones lineales y cuadráticas.
Énfasis: representar la proporcionalidad inversa.
¿Qué vamos a aprender?
En esta sesión aprenderás a representar de manera algebraica, tabular y gráfica, diferentes situaciones tanto de proporcionalidad directa como de proporcionalidad inversa.
Necesitarás para esta sesión tu cuaderno, lápiz, goma y una regla.
Anota en tu cuaderno cualquier inquietud que surja al resolver las situaciones de esta sesión.
¿Qué hacemos?
“Las magnitudes se pueden comparar de varias maneras, una de ellas es la proporcionalidad directa”.
Dos magnitudes son directamente proporcionales si al aumentar una, la otra también aumenta de una manera constante. Dicha constante de proporcionalidad es la razón entre ellas.

Observa el siguiente ejemplo:
Sabes que un metro de cable eléctrico cuesta 12 pesos. Se ha elaborado esta tabla, a partir de ello, ¿cuántas veces aumenta tanto en los valores de “x” como en los valores de “y”?
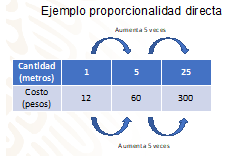
Te puedes dar cuenta que, para ambas magnitudes, cuando una de ellas se hace 5 veces mayor, la otra se hace también 5 veces mayor, respectivamente. Es correcta esa afirmación.
Por otro lado, dos magnitudes son inversamente proporcionales cuando, al aumentar una, la otra disminuye y están relacionadas por un producto constante, el cual, es llamado constante de proporcionalidad.
Así, dos magnitudes son inversamente proporcionales cuando, por ejemplo, una de ella se hace 2, 3, 4 veces mayor y la otra se hace 2, 3, 4 veces menor en la misma proporción.

Observa la siguiente tabla y determina ¿cuántas veces aumentan o disminuyen, tanto los valores de “x”, como los valores de “y”?
Tienes dos magnitudes A y B.
Las magnitudes para A son: 4, 2 y 1.
Las magnitudes para B son: 12, 24 y 48.
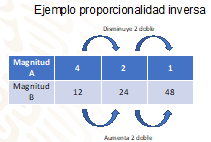
Puedes percatarte que cuando en A, una de sus magnitudes disminuye, la otra aumenta en la misma cantidad respectivamente.
Y en este caso, cuando la magnitud de A disminuye a la mitad, las magnitudes de B aumentan al doble, respectivamente.
Antes de resolver diferentes situaciones de la proporcionalidad directa e inversa, harás un comparativo de ambas proporcionalidades para observar sus diferencias, así tendrás la posibilidad de identificar el tipo de proporcionalidad de acuerdo con sus características.
En la proporcionalidad directa, al aumentar o disminuir una de las variables, la otra aumenta o disminuye, respectivamente, en la misma razón: “A más… más y a menos… menos.”

Por otro lado, en la proporcionalidad inversa, si una de las variables aumenta, la otra disminuye en una misma razón; y si una de las variables disminuye, la otra aumenta en una misma razón: “A más… menos y a menos… más”.
¿Cómo piensas que es la gráfica que representa cada tipo de relación de proporcionalidad?
Observa si coincide con lo que pensaste.
La gráfica en una proporcionalidad directa es una línea recta que pasa por el origen de coordenadas.

Mientras que, la gráfica de una proporcionalidad inversa es una curva llamada hipérbola.
¿Cómo se representa algebraicamente una relación de proporcionalidad directa e inversa?
Considerando a “k” como una constante.
La proporcionalidad directa queda expresada como:
“y” es igual a la “constante” por “x”
Y para la proporcionalidad inversa, queda expresada como:
“y” es igual a la “constante” entre “x”
Entonces, para calcular la constante “k” de la proporcionalidad directa:
La constante es igual a “y” entre “x”

Y para la constante de proporcionalidad inversa:
La constante es igual a “x” por “y”
Ahora, te presentamos diferentes situaciones sobre proporcionalidad, con la finalidad de que identifiques cuáles son directas y cuáles son inversas.
Situación 1.
La siguiente tabla muestra el tiempo que se tarda un elevador en alcanzar tres pisos diferentes de la torre Koi, el cual, es uno de los edificios más altos de México.
Para que el elevador llegue al piso número 4, el tiempo necesario es de 15 segundos que equivale a 0.25 minutos.

Para que el elevador llegue al piso número 16, el tiempo necesario es de 1 minuto.
Y para que el elevador llegue al piso número 64, el tiempo necesario es de 4 minutos.
Con base en esta tabla ¿el número de piso es proporcional al tiempo necesario para que el elevador lo alcance?
La respuesta es: Sí
Ya que la constante es igual, 16 para cada una de las magnitudes
Y como viste en la proporcionalidad directa, al aumentar una de las variables, la otra también aumenta en la misma proporción o razón.
Situación 2.
La siguiente tabla muestra la altura del toronjil morado, una planta medicinal que es endémica de nuestro país, correspondiente a diferentes edades.
En la tercera semana, tiene una altura de 12 cm.

Para la semana 7, tiene una altura de 35 cm.
Para la semana 10, tiene una altura de 60 cm.
¿La altura de la planta es proporcional a su edad?
La respuesta es: No
A pesar de que ambas variables van aumentando, no lo hacen de manera proporcional, su constante no es la misma. Ya que, para 3 semanas, crece 4 veces; para 7 semanas, creció 5 veces y para 10 semanas, lo hizo 6 veces.
Situación 3.
La siguiente tabla muestra una relación entre las variables “x” y “y”.
Cuando “x” vale un cuarto, “y” vale 3.
Cuando “x” vale dos cuartos, “y” vale 6.
Cuando “x” vale tres cuartos, “y” vale 9.
¿La relación entre x y y es o no proporcional?
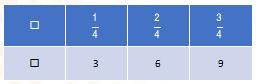
Si contestaron que sí, tu respuesta es correcta.
Ya que, en este caso, ambas variables van en aumento y su constante de proporcionalidad es la misma.
Ahora, resuelve algunos problemas.
Situación 4.
El automóvil de Ismael recorre 16 kilómetros por cada litro de gasolina.
¿Cuántos kilómetros recorrerá con 2, 3, 4 y 5 litros de gasolina? Consideren que siempre recorre 16 kilómetros por litro.
Completa la siguiente tabla:
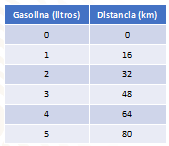
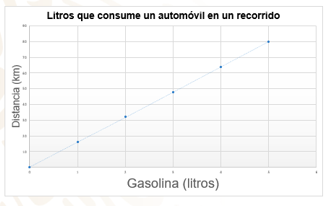
Como podrás observar, la tabla relaciona la gasolina que consume el auto de Ismael con los kilómetros que recorre.
Con 1 litro de gasolina, recorre 16 km.
Con 2 litros de gasolina, recorre 32 km.
Con 3 litros de gasolina, recorre 48 km.
Con 4 litros de gasolina, recorre 64 km.
Con 5 litros de gasolina, recorre 80 km.
Ahora bien ¿este problema se resuelve utilizando proporcionalidad directa o inversa?
Es un problema que se resuelve con proporcionalidad directa, ya que, ambas magnitudes van en aumento y su constante de proporcionalidad es la misma. Para este caso, la constante de proporcionalidad es de 16 para cada una de sus magnitudes.
Observa su representación gráfica.
Observa que la gráfica es una línea recta que pasa por el origen del plano, por lo que se trata de una proporcionalidad directa.
¿Cómo lo puedes representar algebraicamente?
La constante de proporcionalidad se determina con los siguientes datos:
La gasolina expresada en litros, la cual corresponde al valor de “x”.
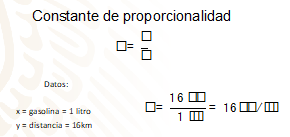
Y la distancia, la cual está expresada en kilómetros, corresponde al valor de “y”.
Al sustituir los valores obtienes 16 kilómetros recorridos entre 1 litro de gasolina, obtienes como resultado: 16 kilómetros por litro.
Para encontrar cualquier valor de “y”, es decir, la distancia que recorre, tienes que multiplicar la constante que es de 16 por el valor de “x”, que, para éste, corresponde a los litros de gasolina.

Sí el automóvil de Ismael consume 24.5 litros de gasolina para ir de la Ciudad de México al puerto de Acapulco ¿cuál es la distancia entre ambos lugares?
Para ello, multiplicas 16 por 24.5 que es igual a 392.
Así, la distancia de Ciudad de México al puerto de Acapulco son 392 km.

Ahora, resuelve y determinar si el siguiente problema es de proporcionalidad directa o inversa.
Situación 5.
La señora Gaudencia quiere cercar uno de sus múltiples terrenos, para ello, puede contratar hasta 4 albañiles.
Necesita saber cuál es el tiempo en que se construirá la cerca si contrata uno, dos, tres o cuatro albañiles.
La Señora Gaudencia ha observado que un albañil levanta un muro en 12 horas, seis lo hacen en dos horas.
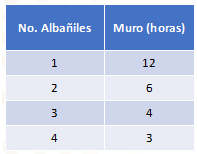
Completa la siguiente tabla para ayudarla en su decisión:
Esta tabla relaciona el número de albañiles con el tiempo que tardan en construir el muro, el cual, está representado en horas.
Si todos los albañiles trabajan al mismo ritmo, considera:
1 albañil tarda 12 horas en construir un muro.
2 albañiles tardan 6 horas en construir un muro.
3 albañiles tardan 4 horas en construir un muro.
4 albañiles tardan 3 horas en construir un muro.
Este es un problema de proporcionalidad inversa.
En donde si una de las variables aumenta, la otra disminuye en un mismo factor.
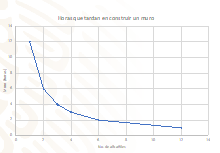
Observa su representación gráfica.
Como puedes darte cuenta, la gráfica es una curva.
Represéntalo algebraicamente. Los datos son:

Número de albañiles, y el tiempo que tardan en hacer el muro, el cual está expresado en horas.
La constante de proporcionalidad, la obtendrás al multiplicar el número de albañiles por las horas.
Al sustituir los valores para saber la constante, obtienes:
1 albañil por 12 horas es igual a 12
2 albañiles por 6 horas es igual a 12
4 albañiles por 3 horas es igual a 12
Como el producto de cada par de valores permanece constante, es el factor de proporcionalidad.
Una vez que tienes el factor de proporcionalidad, puedes representarla con la expresión algebraica:
“y” es igual a constante entre “x”
y = k
x
Por lo que, para encontrar cualquier valor de “y”, es decir, las horas para construir el muro, se divide la constante, que, para este caso, es de 12, entre el valor de “x”, que, para este caso, es el número de albañiles.

Doña Gaudencia sabe ahora los tiempos y puede tomar una decisión, considerando la restricción del problema, donde todos los albañiles trabajan al mismo ritmo.
Analiza otro problema.
Situación 6.
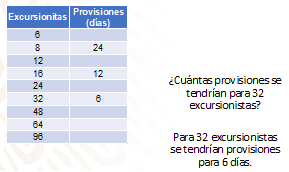
16 excursionistas tienen provisiones para 12 días, si al grupo se agregan 8 personas ¿cuántos días durarán esas mismas provisiones? Considera que todos consumen la misma cantidad de provisiones
¿Para cuántos excursionistas durarían 32 días esas mismas provisiones?
¿Qué tipo de relación de proporcionalidad se establece entre los datos del problema? ¿directa o inversa?
Observa y completa la tabla:

Dicen que para 16 excursionistas se tienen provisiones para 12 días.
Entonces ¿cuántas provisiones se tendrían para 8 excursionistas?

Para 8 excursionistas se tendrían provisiones para 24 días.
Esto obedece a que se reduce a la mitad el número de excursionistas, así que, las provisiones durarán el doble que para 16 personas.
Y, entonces ¿cuántas provisiones se tendrían para 32 excursionistas?

Para 32 excursionistas se tendrían provisiones para 6 días, debido a que se duplicó el número de excursionistas que se tienen de inicio y eso hace que las provisiones se reduzcan a la mitad.
¿Lograron identificar de qué tipo de proporcionalidad se trata? Se trata de una proporcionalidad inversa.
Ya que, si una de las variables aumenta, la otra disminuye en un mismo factor. Ahora bien ¿cómo lo representarán algebraicamente?

Obtienes la constante, la cual es igual al número de excursionistas por el número de las provisiones que consumen al día.
Por lo tanto, la constante es igual a 16 excursionistas por los 12 días, y obtienes que es igual a 192.
Ya teniendo el factor de proporcionalidad, puedes representarla con la expresión algebraica:

“y” es igual a la constante entre “x”
Y así, se pueden encontrar los valores faltantes para “y”.
Si se quiere saber ¿cuántos días durarán esas mismas provisiones para 6 excursionistas?
Se sustituyen las magnitudes en la expresión, quedando de la siguiente manera:
“y” es igual 192 entre 6, obteniendo como respuesta, que les alcanzara para 32 días.

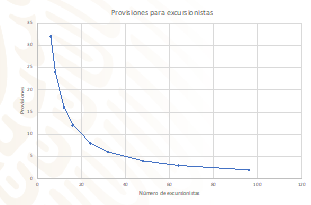
Completa los datos que faltan para poder realizar la gráfica correspondiente.
Compara para saber si llegaste a los mismos resultados:

Traza la gráfica.
Observa cómo nuevamente, tienes una curva.
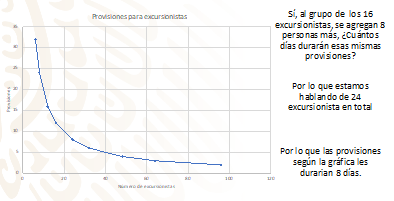
Tomando en cuenta la gráfica, puedes contestar la pregunta del inicio, la cual consiste en saber si al grupo de los 16 excursionistas, se agregan 8 personas más ¿cuántos días durarán esas mismas provisiones?
Como se consideran 24 excursionistas en total, las provisiones, según la gráfica, les durarán 8 días.
Recapitula: a nalizaste datos representados en tablas, gráficas y de manera algebraica, tanto en proporcionalidad directa como inversa.
Siendo las diferencias las siguientes:
En lo referente a la parte gráfica:
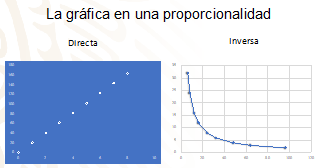
En la proporcionalidad directa la gráfica que la representa es una línea recta que pasa por el origen de las coordenadas; mientras que, para la proporcionalidad inversa, la gráfica es una curva.
Se analiza en la parte tabular:
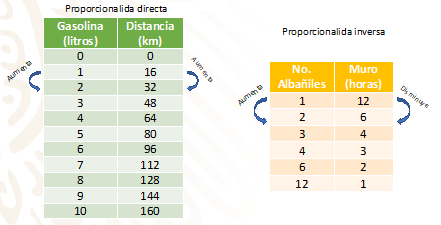
Para la proporcionalidad directa, al aumentar o disminuir una de las variables, la otra aumenta o disminuye, respectivamente, en la misma razón; mientras que, para la proporcionalidad inversa, si una de las variables aumenta, la otra disminuye en una misma razón; y si una de las variables disminuye, la otra aumenta en una misma razón.
Estudiaste que en la parte algebraica:
En la proporcionalidad directa se representa con la expresión:
“y” es igual a la constante por “x”
Mientras que, para la proporcionalidad inversa, se representa con la expresión:
“y” es igual a la constante entre “x”
Conociste cómo determinar las constantes de proporcionalidad:

En el caso de la constante de proporcionalidad directa, se representa como:
Constante es igual a “y” entre “x”
Mientras que, para determinar la constante de proporcionalidad inversa, se representa como:
Constante es igual “x” por “y”
El reto de hoy:
Te recomendamos tener presente lo que trabajaste en esta sesión, p ara leer y representar, tanto de manera gráfica, como algebraicamente, relaciones lineales y cuadráticas, esto te servirá para representar mejor diversos fenómenos en distintos contextos.
En esta sesión aprendiste “las d iferencias que existe entre la proporcionalidad directa y la proporcionalidad inversa ”, las cuales representas de manera algebraica, tabular y gráfica, en diferentes situaciones y problemas.
Es importante que busques, en tu libro de texto de Matemáticas de tercer grado, problemas y ejercicios similares a los que estudiaste en esta sesión, para que los resuelvas y practiques lo que aprendiste.
Recuerda que, sin autodisciplina, el éxito es imposible.
¡Buen trabajo!
Gracias por tu esfuerzo.


Login to join the discussion