Proporcionalidad directa III
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:07
Proporcionalidad directa III
Aprendizaje esperado: analiza y compara situaciones de variación lineal y proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la física y otros contextos.
Énfasis: analizar y comparar situaciones de proporcionalidad directa a partir de sus representaciones tabular, gráfica y algebraica.
¿Qué vamos a aprender?
Continuarás con el estudio de proporcionalidad directa. En esta sesión, analizarás situaciones para la resolución de problemas a partir de sus representaciones algebraica, tabular y gráfica.
¿Qué hacemos?
Reflexiona sobre los siguientes planteamientos:
- ¿Es posible identificar en una fórmula de física, si las variables están relacionadas a través de la variación directa?
- ¿Qué condiciones deben de cumplirse para que una expresión algebraica modele una situación de proporcionalidad directa?
- ¿Cómo es la gráfica de una relación de proporcionalidad directa?
Registra tus reflexiones. A través de diversas situaciones y problemas, construirás las respuestas a éstas y otras preguntas.
Para iniciar con el tema de esta sesión, considera lo siguiente: ¿qué pesa más, un kilogramo de algodón o un kilogramo de plomo?, ¿cuál ocupa más espacio?
1 kilogramo de algodón pesa lo mismo que 1 kilogramo de plomo, pero dependiendo del material, puede ser una misma cantidad de masa. Por ejemplo, 1 kilogramo de algodón puede ocupar más espacio que 1 kilogramo de plomo si no se comprime, o menos espacio si está comprimido.
Ahora, analiza:
¿Qué ocupará más espacio, un centímetro cúbico de corcho o un centímetro cúbico de plomo?, ¿cuál pesará más?
Responde las preguntas anteriores y justifica tus respuestas.
Un centímetro cúbico de corcho ocupa la misma cantidad de espacio que un centímetro cúbico de plomo. Sin embargo, un centímetro cúbico de plomo tiene una masa mayor; por lo tanto, el plomo pesa más. Pero ¿por qué sucede esto?
La cantidad de masa de un material que cabe en una unidad de volumen se llama densidad. La densidad del plomo es de:
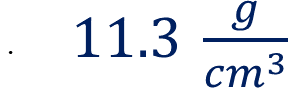
Esto significa que la masa de un centímetro cúbico de plomo es 11.3 gramos.
Por otro lado, la densidad del aluminio es de:

Y la del agua:
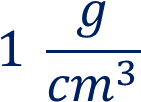
Ahora, presta atención a la siguiente información, pues te servirá para resolver las situaciones-problema que se presentarán más adelante.
Si “m” representa la masa y “v” el volumen, la expresión algebraica de la densidad "D" es la siguiente:

Reflexiona en torno a las siguientes preguntas:
¿Qué pasa con la densidad si el volumen aumenta y la masa permanece igual?
¿Qué pasa con el volumen si la masa aumenta y la densidad es la misma?
Registra tus ideas. Conforme avances en la sesión podrás fortalecerlas o modificarlas.
Ahora, toma como referencia lo anterior y analiza la siguiente situación de proporcionalidad directa, a partir de sus representaciones algebraica, tabular y gráfica.
Relación masa-volumen
Completa la siguiente tabla de datos que permite relacionar la masa y el volumen para distintas cantidades de aluminio.

Primero, calcula la masa que hay en un centímetro cúbico. Para ello, considera el valor de la densidad del aluminio, que tomará el valor de la constante de proporcionalidad “k”, y éste es igual a:

La expresión para calcular la segunda magnitud en una proporcionalidad directa “y”, es igual a la constante de proporcionalidad “k”, por su correspondiente de la primera magnitud “x”; por lo tanto, si se necesita encontrar la masa de un centímetro cúbico de aluminio, se puede recurrir a la siguiente fórmula:
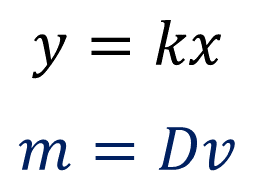
Sustituyendo los datos en la fórmula se tiene que:
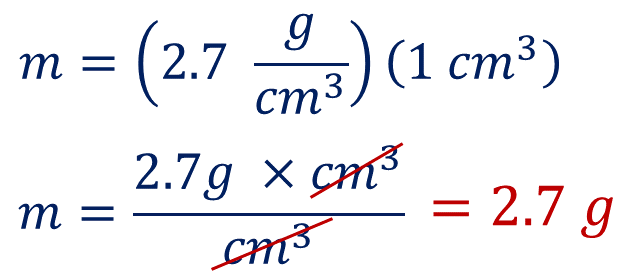
Por lo tanto, se obtienen 2.7 gramos.
Ahora, determina el volumen que ocupa una masa de 13.5 gramos.

¿Qué piensas que se necesita realizar para determinar el volumen que ocupa una masa de 13.5 gramos?, ¿qué dato o datos de los que ya se tienen se deben considerar para este cálculo?
Para calcular el volumen que hay en una masa de 13.5 gramos, utilizarás el valor de la densidad del aluminio, que tomará el valor de la constante de proporcionalidad “k”, es decir:

La expresión para calcular la primera magnitud en una proporcionalidad directa “x” es igual a la segunda magnitud “y” entre la constante de proporcionalidad “k”; por lo tanto, si se quiere encontrar el volumen de una masa de 13.5 gramos de aluminio, se puede utilizar la siguiente fórmula:
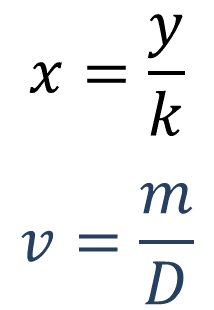
Sustituyendo los datos en la fórmula se tiene que:
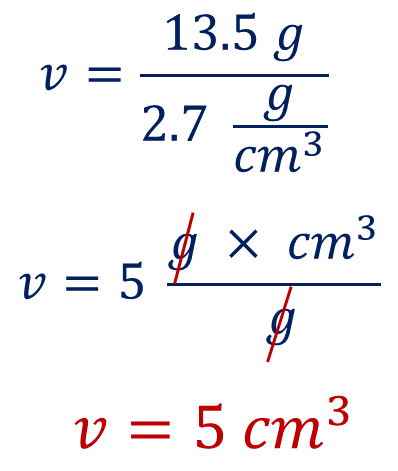
Por lo tanto, 13.5 gramos de masa ocupan 5 centímetros cúbicos.
Continúa con la masa que hay en 10 centímetros cúbicos.

¿Ya pensaste en alguna forma de hacerlo?, ¿cómo ocuparías la densidad del aluminio para realizar el cálculo que se necesita?
Para calcular la masa que hay en 10 centímetros cúbicos, lo primero que necesitas hacer es tomar el valor de la densidad del aluminio como el valor de la constante de proporcionalidad “k”, que es igual a:

Para calcular la segunda magnitud en una proporcionalidad directa, “y” es igual a la constante de proporcionalidad “k” por su correspondiente de la primera magnitud “x”; por lo tanto, si se quiere encontrar la masa de 10 centímetros cúbicos de aluminio, se puede utilizar la siguiente fórmula:
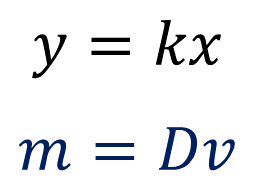
Sustituyendo los datos en la fórmula se tiene que:
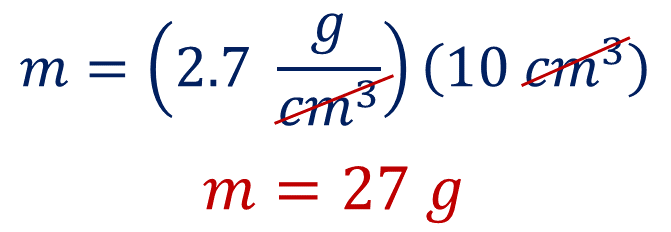
Obteniendo 27 gramos, que corresponden a la masa que hay en 10 centímetros cúbicos de aluminio.
Finalmente, en la tabla falta el dato del volumen que corresponde a una masa de 32.4 gramos de aluminio.

Con lo trabajado hasta el momento, contesta lo siguiente: ¿qué se puede hacer para calcular ese dato?
Para calcular el volumen que hay en una masa de 32.4 gramos, usarás el valor de la densidad del aluminio, que tomará el valor de la constante de proporcionalidad “k” y que es igual a:

La expresión para calcular la primera magnitud en una proporcionalidad directa “x” es igual a la segunda magnitud “y” entre la constante de proporcionalidad “k”; por lo tanto, si se quiere encontrar el volumen de una masa de 32.4 gramos de aluminio, se utiliza la siguiente fórmula:
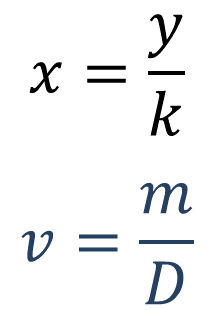
Sustituyendo los datos en la fórmula se tiene que
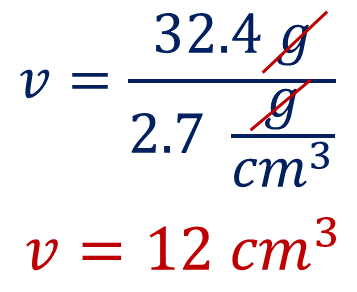
Obteniendo 12 centímetros cúbicos. Esto permite afirmar que una masa de 32.4 gramos de aluminio tiene un volumen de 12 centímetros cúbicos.
Has completado la tabla con una relación entre masa y volumen para distintas cantidades de aluminio. Ahora encuentra los puntos coordenados o coordenadas en una tabulación y represéntalas de forma gráfica.
En la tabla, cada punto coordenado se nombra utilizando letras mayúsculas y colocando dentro de un paréntesis los valores ordenados de “x” y de “y”. Por lo tanto, en la primera columna se anotan los valores de “x” que representan el volumen en centímetros cúbicos del aluminio; en la segunda columna se registran los valores de “y”, es decir, la masa del aluminio, y en la tercera columna, los puntos coordenados o coordenadas que están definidos como:
Punto "A" (1, 2.7)
Punto "B" (5, 13.5)
Punto "C" (10, 27)
Punto "D" (12, 32.4)
Con la información anterior, la tabla queda de la siguiente manera:
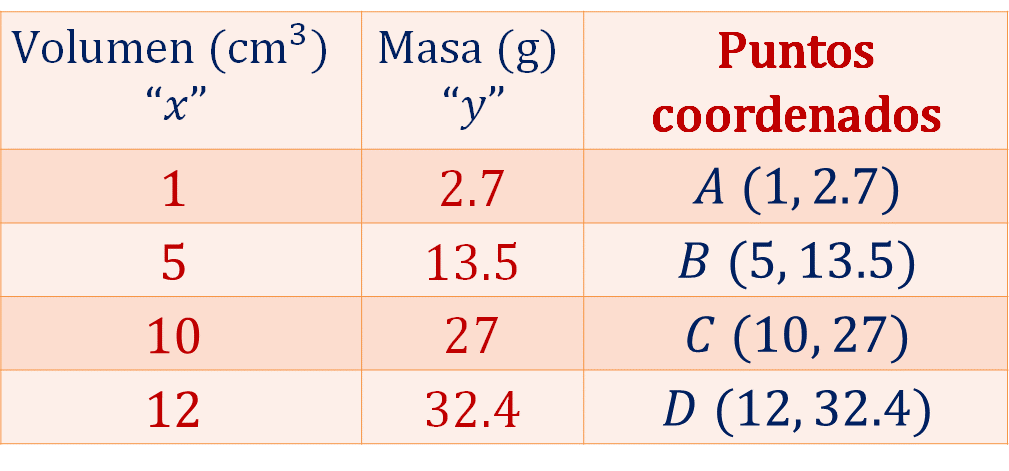
Ahora, traza la gráfica de la relación masa-volumen. En el eje horizontal se representa el volumen en centímetros cúbicos; en el eje vertical se representa la masa en gramos. Entonces, se ubican las coordenadas “x” y “y” que se obtuvieron en la tabulación.
Ubica el punto "A" (1, 2.7); la coordenada "B" (5, 13.5); la coordenada "C" (10, 27); y finalmente, la coordenada "D" (12, 32.4)
Ya que están ubicados los puntos, traza una línea que pase sobre los puntos identificados con su correspondiente letra mayúscula, como se muestra en la siguiente imagen.
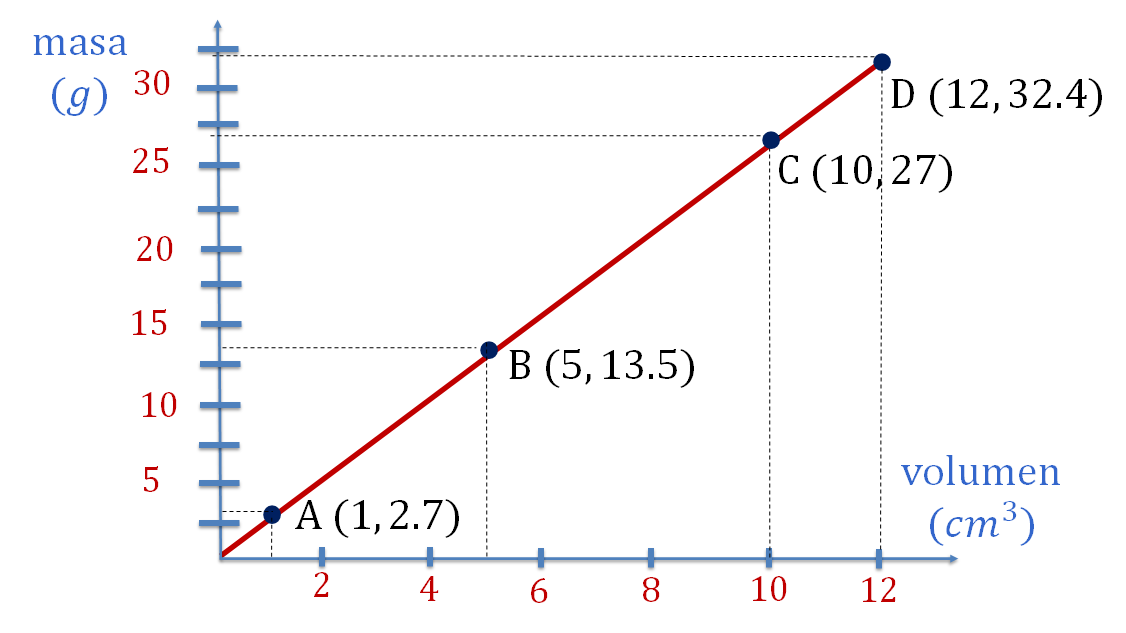
Ya tienes la representación gráfica de la relación masa-volumen.
De esta manera, se puede confirmar que los datos del planteamiento se relacionan a través de una proporcionalidad directa, porque las dos magnitudes son directamente proporcionales. Es decir, cuando una de ellas aumenta, la otra también y lo hace en la misma proporción, o si una disminuye, la otra también en la misma proporción.
Al observar la gráfica, las coordenadas "A" y "B" tienen una proporción directa, el valor de “x” en la coordenada "A" es igual a 1 y en la coordenada "B" es igual a 5, hubo un aumento de 5 veces; esta proporción se ve reflejada en el valor de “y”, donde en la coordenada "A" es igual a 2.7 y aumenta cinco veces en la coordenada "B", que es igual a 13.5
Para reforzar lo aprendido hasta el momento, analiza la siguiente situación-problema.
Relación tiempo-radio
Si se lanza una piedra a un estanque:
- ¿Qué sucede?
- ¿Alguna vez has arrojado una piedra el agua?
- ¿Qué se forma?
Cuando se lanza una piedra a un estanque se forman círculos concéntricos en la superficie del agua. El radio (r) del círculo mayor está dado por (r = 0.6 t), donde “t” es el tiempo transcurrido, en segundos, a partir de que la piedra se lanza y hasta que toca el agua. La expresión resultó después de experimentar varias veces el lanzamiento.

- ¿Esta situación corresponde a una relación de proporcionalidad directa?
- ¿Cuál es el radio del círculo mayor si la piedra tarda en chocar 4, 6 y 10 segundos en el agua?
Para contestar lo anterior, utilizarás la siguiente expresión o fórmula:
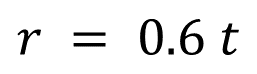
Donde:
r: representa el radio del círculo que se forma cuando la piedra choca en el agua, medido en centímetros.
t: el tiempo en segundos, que transcurre desde que la piedra se lanza, hasta chocar con el agua.
Sustituyendo los datos, se obtienen los siguientes valores:
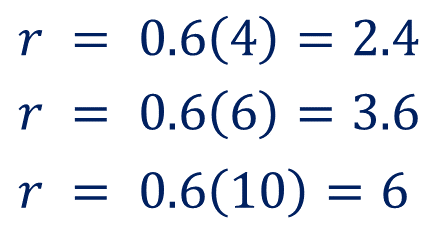
Esto quiere decir que cuando la piedra tarda 4 segundos en chocar con el agua, forma un círculo con radio igual a 2.4 cm; cuando tarda seis segundos forma un círculo con radio igual a 3.6 cm. Y cuando la piedra choca con el agua después de 10 segundos, forma un círculo con un radio igual a 6 centímetros.
Continúa ahora con la gráfica de esta situación.
En la tabla de la relación tiempo-radio, a cada punto se le nombrará utilizando letras mayúsculas y colocando dentro de un paréntesis los valores ordenados de “x” y de “y”. Recuerda que siempre el primer valor será el de las abscisas o de las “x”, y el segundo valor será el de las ordenadas o de las “y”
Por lo tanto, en la primera columna se anotan los valores de “t”, que representa el tiempo que transcurre desde que se lanza la piedra y hasta que choca con el agua, sus unidades están dadas en segundos. En la segunda columna se registran los valores de “r”, que corresponden al radio del círculo que se forma cuando la piedra choca en el agua, medido en centímetros. Por último, en la tercera columna se colocan los puntos coordenados o coordenadas que están definidos como:
Punto "A" (4, 2.4)
Punto "B" (6, 3.6)
Punto "C" (10, 6)
Con esta información, la tabla queda de la siguiente manera:
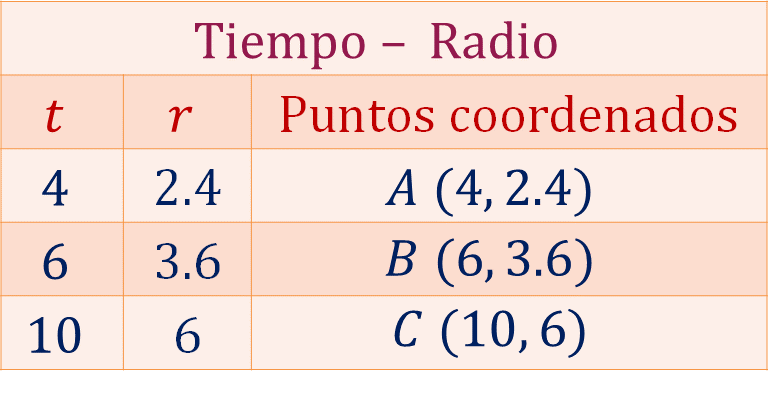
Ahora, traza la gráfica radio-tiempo. En el eje horizontal se encuentra el tiempo en segundos, en el eje vertical se tiene al radio en centímetros.
Ubica las coordenadas (x, y) que se obtuvieron de la tabla. Inicia con el punto "A" (4, 2.4); sigue con el punto "B" (6, 3.6); finalmente, ubica el punto "C" (10, 6).
Ya que están ubicadas las coordenadas, traza una línea que pase sobre los puntos identificados con su correspondiente letra mayúscula, como se muestra en la siguiente imagen.
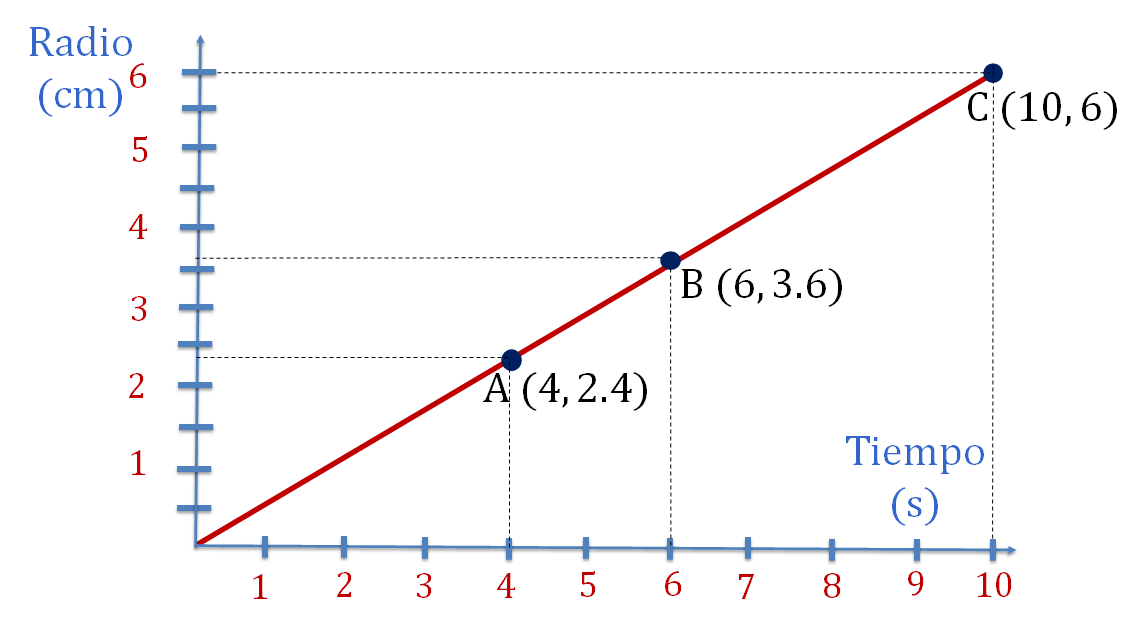
Ya tienes la representación gráfica de una proporción directa tiempo-radio.
Reflexiona: ¿qué se debe observar en la gráfica para afirmar que esta es una situación de proporcionalidad directa?
Ahora, continúa con otra situación.
Relación pesos mexicanos-dólares
Analiza la siguiente gráfica que muestra la relación que existe entre los pesos mexicanos y los dólares.
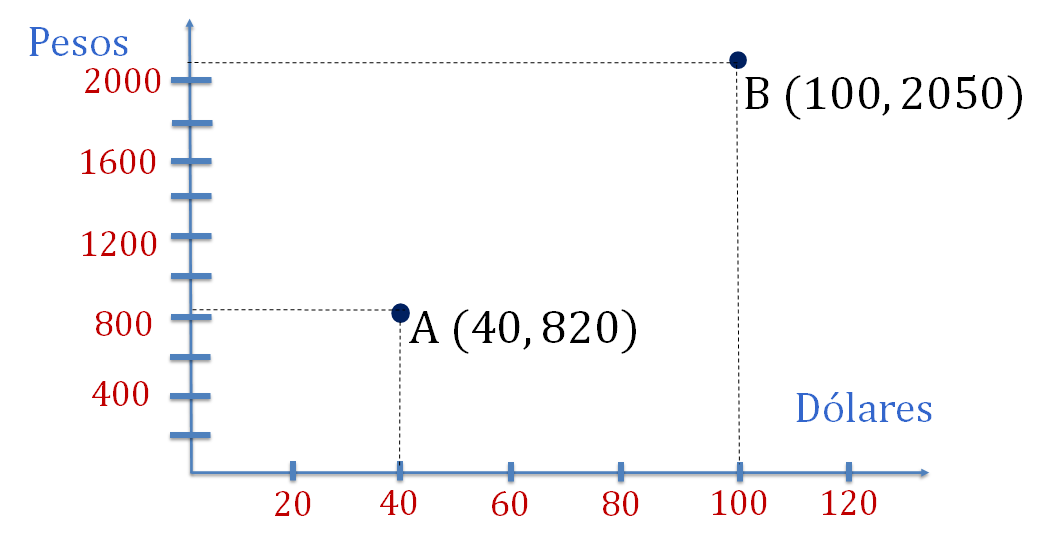
La gráfica de la relación pesos-dólares, muestra en el eje horizontal o eje de las abscisas a los dólares, en el eje vertical o eje de las ordenadas a los pesos; por lo tanto, un punto coordenado o una coordenada es representada con un valor del eje “x” dólares y otro del eje “y” pesos. Piensa si esta situación es de proporcionalidad directa e identifica en la gráfica lo que te permita realizar tu afirmación.
- La primera coordenada mostrada en la gráfica es el punto "A" (40, 820).
- La segunda coordenada ubicada en la gráfica es el punto "B" (100, 2050).
Ya ubicados las coordenadas, traza una línea que pase sobre los puntos identificados, como se muestra en la siguiente imagen.
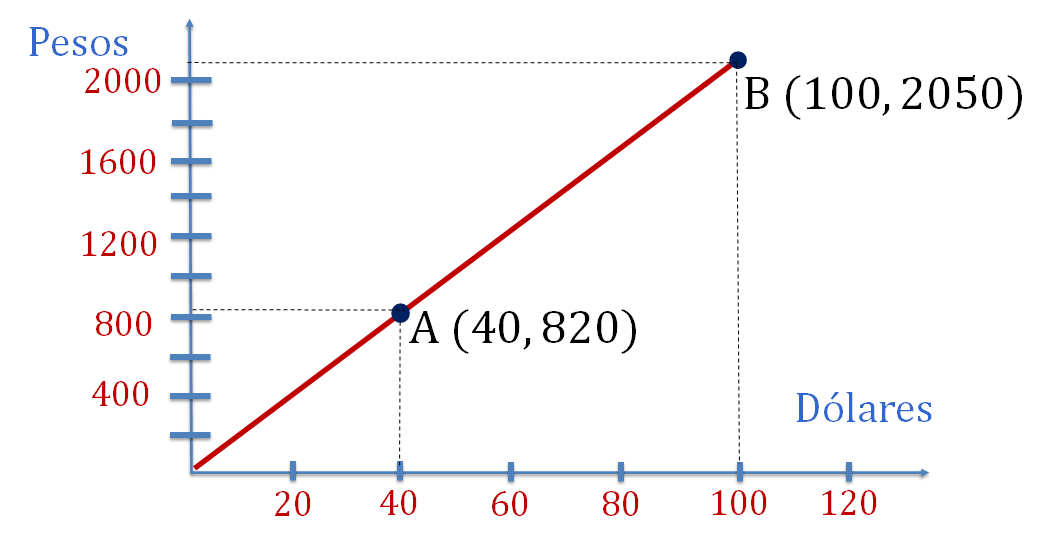
Ya tienes la representación gráfica de una proporción pesos-dólares.
Ahora, analiza las siguientes preguntas:
¿Qué datos se pueden obtener a partir de esta gráfica, viendo sus características?, ¿puedes decir si corresponde a una situación de proporción directa?, ¿sería posible encontrar una expresión que modele esta situación?
Al realizar la división de la ordenada entre la abscisa con cualquiera de las dos parejas de valores (coordenadas), se obtiene un valor. ¿Qué representa el cociente obtenido?
Como lo has estudiado, si se divide un número de la segunda magnitud “y” entre su correspondiente en la primera magnitud “x”, se obtiene la constante de proporcionalidad, en este caso, el costo de un dólar.
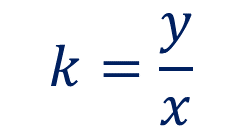
Tomando en cuenta las dos coordenadas, lo primero que harás será completar una tabla de la siguiente forma: coordenada "A" (40, 820), el primer valor de la coordenada representa los dólares y el segundo valor su equivalencia en pesos, por lo tanto, cuarenta dólares equivalen a ochocientos veinte pesos.
Para la coordenada "B" (100, 2050), el primer valor de la coordenada representa los dólares y el segundo valor su equivalencia en pesos, por lo tanto, cien dólares equivalen a dos mil cincuenta pesos.

La constante de proporcionalidad se calcula dividiendo el número de la segunda magnitud, “y”, entre su correspondiente en la primera magnitud, “x”.
Empieza con la sustitución de los valores de la primera fila
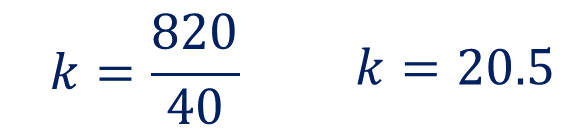
Por lo tanto “k” es igual a 20.5
Continúa con la segunda fila
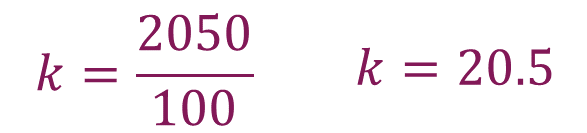
Se obtiene el valor: “k” igual a 20.5.
De este modo, se puede afirmar que los valores de la gráfica representan un problema de proporcionalidad directa ya que al dividir cada número de la segunda magnitud “y” entre su correspondiente en la primera magnitud “x”, se obtiene el mismo número, es decir, los cocientes son constantes.
Reflexiona:
¿Cuál es la expresión algebraica o fórmula que permite convertir los dólares a pesos mexicanos?
Al tomar en cuenta la constante de proporcionalidad que se obtuvo en el inciso anterior, “k” es igual a 20.5 y recordando que en las sesiones anteriores se estableció la expresión para calcular la segunda magnitud en una proporcionalidad directa como:
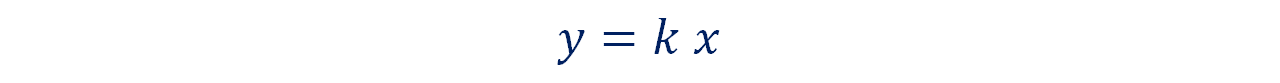
Se puede afirmar que la expresión algebraica que corresponde a esta situación es:
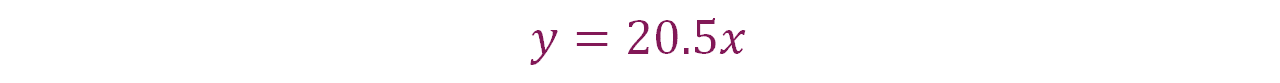
Donde:
y: es la cantidad en pesos.
x: la cantidad en dólares.
Después de haber obtenido la expresión algebraica para convertir los dólares americanos a pesos mexicanos, ¿cuántos pesos mexicanos equivalen a trescientos veinte dólares americanos?
Tomando en cuenta la expresión algebraica, “y” es igual a 20.5 por el valor de la primera magnitud, se puede calcular la equivalencia de los trescientos veinte dólares a pesos mexicanos.
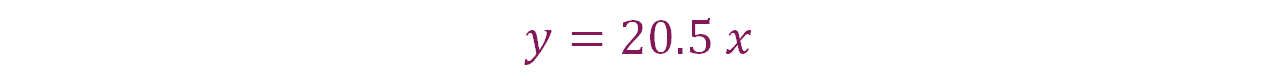
Sustituye los datos:
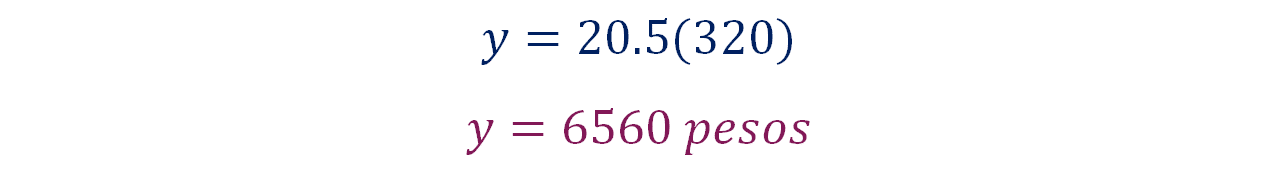
Por lo tanto, se obtiene que “y” es igual a 6,560 pesos.
Entonces, ¿esta situación es de proporcionalidad directa?
La relación pesos mexicanos y dólares americanos, están relacionados a través de la proporcionalidad directa.
Has finalizado. En esta sesión, analizaste situaciones de proporcionalidad directa, a partir de sus representaciones algebraica, tabular y gráfica para la resolución de problemas. Ejemplo de ello fueron: a mayor volumen, mayor masa, el radio de un círculo después de que choca una piedra en el agua y la conversión de dólares a pesos mexicanos.
El reto de hoy:
Resuelve algunos de los problemas o ejercicios sobre proporcionalidad directa de tu libro de texto de Matemáticas, de segundo grado.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion