Propiedades de la igualdad

Aprendizaje esperado: resuelve problemas mediante la formulación y solución algebraica de sistemas de dos ecuaciones lineales con dos incógnitas.

Énfasis: dar sentido y significado a las propiedades de la igualdad.

¿Qué vamos a aprender?

Profundizarás en la resolución de problemas mediante sistemas de dos ecuaciones lineales con dos incógnitas. En esta sesión, identificarás las propiedades de la igualdad; como la propiedad uniforme, la propiedad cancelativa y la propiedad simétrica; y las aplicarás.

¿Qué hacemos?

Para iniciar, reflexiona en las siguientes preguntas:

¿Qué es una igualdad?

¿Qué relación hay entre una ecuación y una igualdad?

¿Qué es una propiedad?

¿Cuáles son las propiedades de las igualdades?

¿Cómo puedes aplicarlas con sentido y significado en la resolución de problemas?

Las definiciones son un punto de partida, pues, es natural que si alguno de los términos que se mencionan en los planteamientos matemáticos son desconocidos, generalmente se busca su significado en un diccionario de matemáticas, en el libro de texto o en otro medio electrónico o impreso considerado una fuente confiable. Pero al resolver problemas es cuando se puede dar sentido y significado a estas.

Por ello, analiza la información, comprende los procedimientos y busca respuesta a las dudas o dificultades.

Para resolver ecuaciones, es necesario aplicar las propiedades de la igualdad para obtener el valor de la o las incógnitas involucradas. El signo de igualdad representa una relación entre números y expresiones matemáticas. Toma esto como base del conocimiento.

Retomando la reflexión sobre qué es una igualdad, se puede decir que una igualdad es una relación de equivalencia donde dos expresiones matemáticas representan el mismo valor.

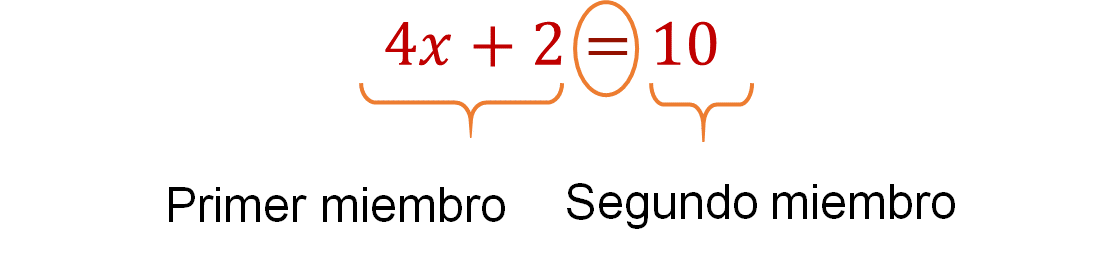
Hay una relación de equivalencia entre la expresión 4x + 2 y diez, establecida por el signo de igual, que divide en dos miembros a la igualdad, al de la izquierda se le denomina primer miembro y al de la derecha segundo miembro de la igualdad.

Para operar los términos de una igualdad, debes considerar el tipo y los efectos de las operaciones que se establecen entre las expresiones matemáticas, éstas pueden ser aditivas o multiplicativas, es decir: adiciones, sustracciones, multiplicaciones o divisiones, entre otras.

Las operaciones mencionadas son inversas una de otra: la suma y la resta son operaciones inversas, ya que una contrarresta el efecto de la otra. Lo mismo sucede con la multiplicación y la división.

¿Para qué sirve conocer las operaciones inversas?

Conocerlas es útil para resolver una ecuación, ya que debes dejar en un sólo miembro de la igualdad al término que contiene a la incógnita. Analízalo con la ecuación planteada anteriormente.

Como puedes observar, en el primer miembro de la igualdad (además del término que contiene a la incógnita “x”), también se encuentra el número dos, que en este caso está afectado por la operación suma, se sabe que la operación inversa a la adición es la sustracción.

Una manera de eliminar este término del primer miembro es aplicar la propiedad de la igualdad denominada, Propiedad uniforme, que establece que, si se suma o se resta la misma cantidad en ambos miembros, la igualdad se conserva. Por ejemplo:

Aplicando esta propiedad de la igualdad a la ecuación planteada, como en el primer miembro hay un dos que está sumando, se utiliza la operación inversa a la adición, teniendo presente la propiedad uniforme que se acaba de mencionar. Para mantener la equivalencia en la expresión, hay que restar el número dos en el primer miembro, y también hacerlo en el segundo miembro. Por lo tanto:

Ahora tienes una expresión equivalente a la ecuación anterior, que se lee, 4 “x” es igual a ocho. La incógnita “x”, sigue estando afectada por un número, el cuatro.

¿Qué operación efectúa el 4 a la “x”?

La está multiplicando.

Aplicando nuevamente la propiedad uniforme de la igualdad, se utiliza la operación inversa a la multiplicación para simplificar el número cuatro; por ello, en ambos miembros de la igualdad se divide por cuatro, manteniendo así la igualdad.

Como la cuarta parte de 4x es “x” y la cuarta parte de ocho es dos, entonces el resultado de las operaciones es la igualdad: x = 2. Has encontrado el valor de la incógnita de esta ecuación.

Como ya sabes, debes comprobar que el valor de este resultado se cumpla en la ecuación inicial. La comprobación es un paso importante en la resolución de problemas, pues brinda la oportunidad de verificar los cálculos.

Realiza la comprobación.

Diez es igual a diez, se comprueba satisfactoriamente el valor de la incógnita que se encontró.

Continúa con otro ejercicio, ahora tienes la igualdad:

En ambos miembros de la igualdad existe el término “3y” que está sumando, para eliminarlo de la igualdad utiliza la propiedad cancelativa de la igualdad. La cual establece que, si en ambos miembros existen términos iguales, éstos pueden suprimirse y la igualdad se mantiene.

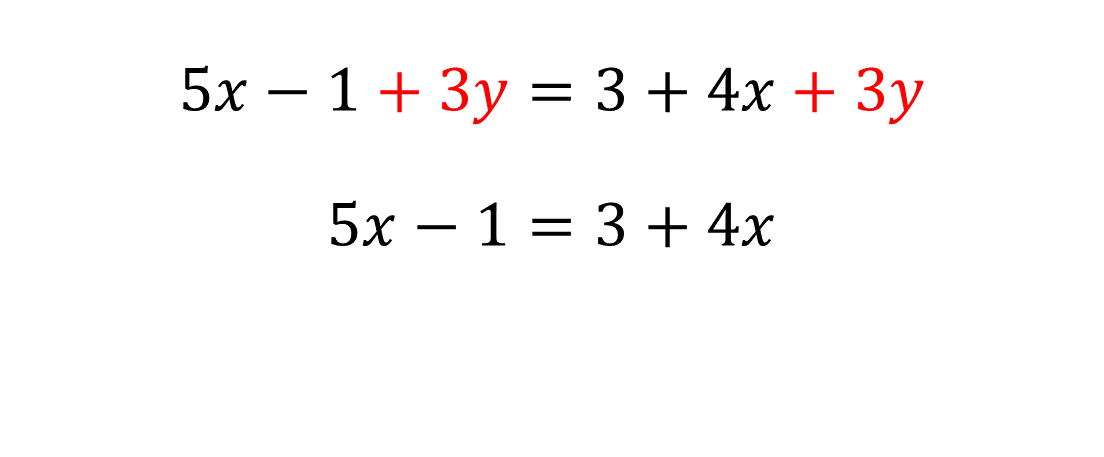
Después de obtener la expresión resultante, se puede notar que, en ambos miembros existen términos que contienen la incógnita, además de otros términos.

El siguiente paso en la solución de esta ecuación es acomodar en un sólo miembro de la igualdad a los términos que contienen la incógnita.

Convencionalmente se trasladan al primer miembro de la igualdad y los que no la contienen, al segundo miembro; aunque las incógnitas también se pueden acomodar en el segundo miembro, debido al sentido de equivalencia.

Para lograrlo, debes observar qué operación está realizando el término de la incógnita en el segundo miembro; en este caso, 4x se está sumando. Para suprimir ese sumando, debes restar el mismo valor, teniendo presente la propiedad uniforme de la igualdad. Por lo tanto, resta en ambos miembros de la igualdad el término cuatro equis.

Quedando la expresión equivalente, x - 1 = 3.

Siguiendo el mismo procedimiento, basado en la propiedad uniforme de la igualdad, puedes observar que la incógnita está afectada por el número uno en el primer término de la igualdad, el cual está realizando la operación resta, esto nos lleva a plantear la operación inversa, que es la suma.

Debes entonces, sumar en ambos miembros de la igualdad a uno, para suprimir en el primer miembro el término que no contiene a la incógnita:

Has encontrado el valor de la incógnita. “x” es igual a cuatro.

Ahora, realiza la comprobación y corrobora que con este número se satisface la igualdad.

Para manipular los términos de una igualdad, debes tener presentes las propiedades de la igualdad, las que has visto hasta ahora son: la propiedad uniforme y la propiedad cancelativa, para aplicarlas hay que considerar las operaciones inversas, pues gracias a ellas se puede ir dejando únicamente al término que contiene a la incógnita en uno de los miembros.

Quizá, has escuchado la expresión “lo pasamos al otro lado” cuando se resuelven problemas de este tipo, ya que es una expresión usada comúnmente, y hace referencia a la abreviación del procedimiento que se acaba de realizar, pues, cuando hay un número sumando en un miembro de la igualdad, al hacer la operación inversa, pareciera como si el mismo término, “pasara del otro lado del signo igual” efectuando la operación contraria, para el caso de la suma, la resta. En el caso de la multiplicación y la división, parece que lo que se pasa de un miembro a otro son factores.

La expresión “pasa del otro lado”, se escucha frecuentemente al trabajar la manipulación de términos. Y se emplea tanto para los términos que se suman y se restan, así como para los factores que se multiplica y dividen.

Continúa con el siguiente ejemplo.

Tienes ahora la ecuación:

En este ejemplo, en el primer miembro se tienen dos términos, el que contiene la incógnita y el cinco que está restando, para suprimirlo del primer miembro, debes sumar en ambos miembros cinco; pues eso indica la propiedad uniforme.

De manera abreviada, el cinco del primer miembro que está restando, “lo pasamos” al segundo miembro realizando la operación inversa, es decir, sumando.

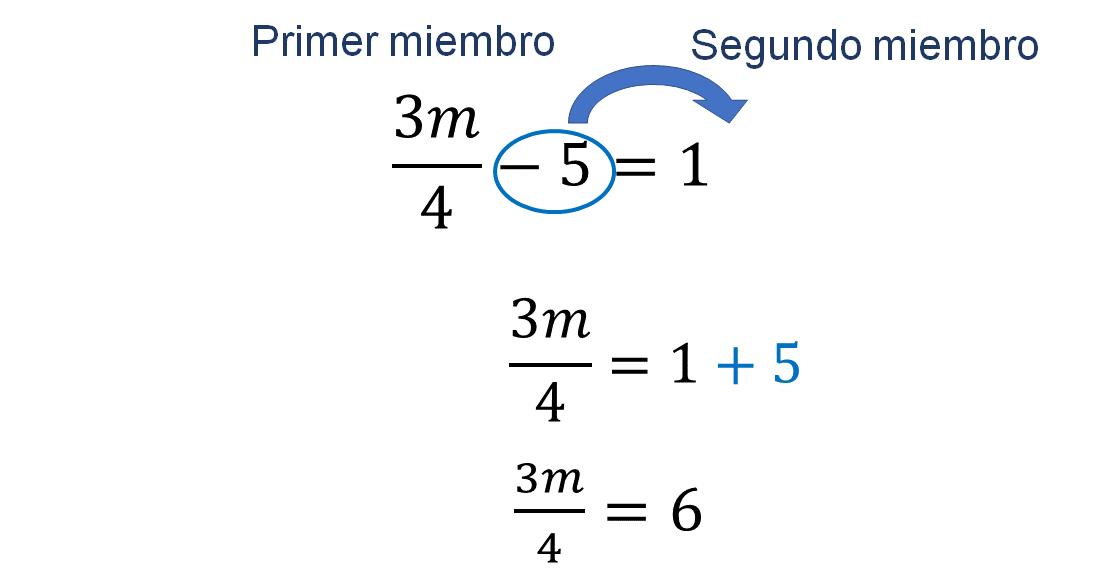
Ahora tienes una nueva expresión equivalente a la primera. Observa que la incógnita “m”, aún está siendo afectada por los números cuatro y tres.

El siguiente paso es quitar el cuatro del primer miembro, la operación que realiza es la división, por lo tanto, para simplificarlo del primer miembro, debes multiplicar por cuatro, teniendo presente la propiedad uniforme de la igualdad, multiplica por cuatro ambos miembros para conservar la igualdad.

Se podría expresar de manera abreviada como, el cuatro que está realizando una división en el primer miembro “pasa al segundo miembro” multiplicando al seis, lo que da como resultado tres “m” es igual a seis por cuatro, que equivale a veinticuatro.

Tienes ahora la expresión 3m = 24.

La incógnita sigue estando afectada, ahora por el factor tres, por lo que, debes dividir en ambos miembros de la igualdad por tres, para poder simplificar del primer miembro el factor tres.

Dicho de otra manera, el tres que multiplica a la incógnita en el primer miembro pasa al segundo miembro de la igualdad dividiendo, en este caso, el tres divide al veinticuatro, teniendo como resultado “m” igual a ocho.

Has resuelto la ecuación.

Como has podido observar, la frase “pasa del otro lado” es, efectivamente, una abreviación de realizar la operación inversa de un término en ambos miembros de la igualdad.

Es importante notar que, en la ecuación anterior, se denominó a la incógnita con la letra “m” y no con la “x” como tradicionalmente se hace. En el trabajo algebraico, y en general en las matemáticas, pueden existir variantes y no siempre se te presentarán las mismas literales o expresiones cuando debas resolver ecuaciones.

Observa que en el caso de las ecuaciones debes interpretar a la literal como una incógnita, es decir, tienes que obtener mediante las propiedades de la igualdad, su valor.

Aplica las propiedades de la igualdad resolviendo el siguiente problema.

Problema Sofia

Sofía necesita colocar una barda en su terreno que es de forma rectangular, sabe que tiene un área de 285 metros cuadrados y tiene un lado que mide diecinueve metros, ¿cuántos metros medirá la longitud de la barda?

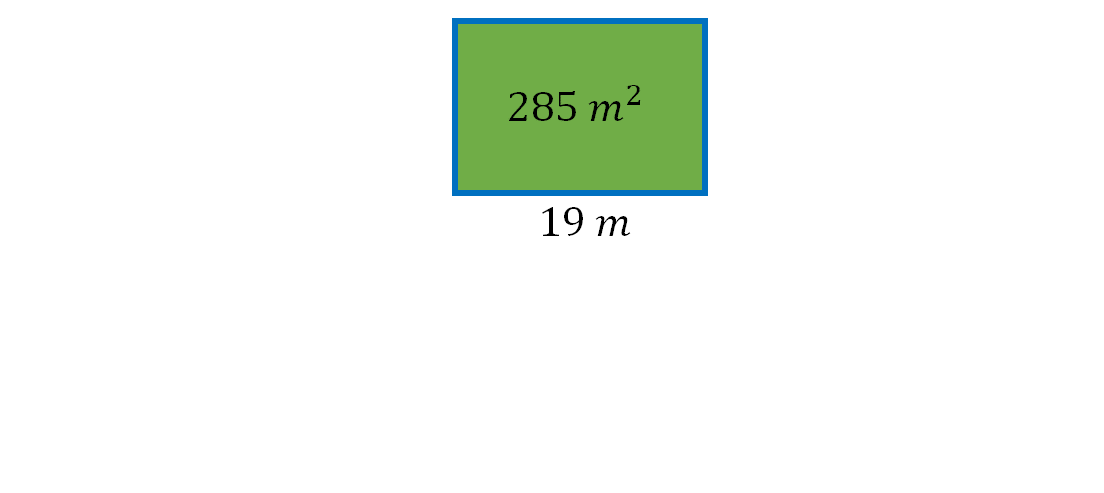
Para dar solución a este problema, debes analizar los datos que conoces, en este caso, la forma del terreno es rectangular, su área es de 285 metros cuadrados y tiene un lado de diecinueve metros.

Entonces, necesitas conocer la longitud de la barda, que es equivalente al perímetro del terreno.

Con los datos que tienes no puedes calcular el perímetro, pues necesitas la medida del otro lado del terreno.

La medida del lado desconocido se encuentra planteando la fórmula del área del terreno rectangular, ya que como sabes, el área del rectángulo está dada por el producto del largo, por el ancho. En este caso, considera la medida de diecinueve metros como la medida del largo.

Establece ahora con los valores conocidos, la fórmula del área.

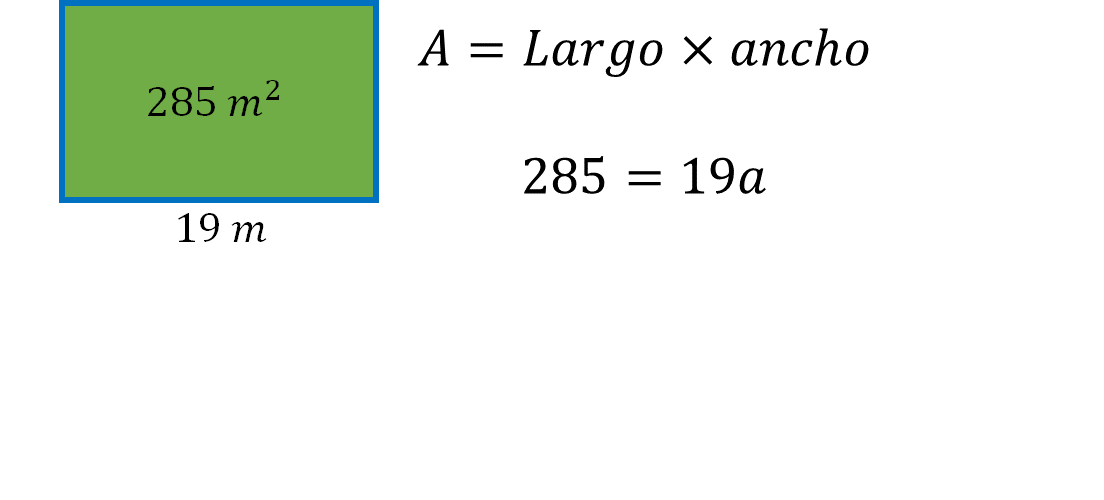
Al escribir el planteamiento para calcular el área, tienes una incógnita en el segundo miembro de la igualdad, convencionalmente como se dijo anteriormente, se trasladaron las incógnitas al primer miembro de la igualdad, por ello, vas a utilizar otra propiedad de la igualdad denominada propiedad simétrica, la cual establece que, los miembros de la igualdad pueden cambiarse de orden sin que se afecte la igualdad, en este caso tienes que:

Ahora tienes a la incógnita “a” (que representa el ancho del terreno), en el primer miembro de la igualdad.

El paso siguiente es manipular los factores para dejar sola a la incógnita, que en este caso está siendo afectada por el diecinueve con la operación multiplicación.

Realizando el procedimiento, debes dividir ambos miembros de la igualdad por diecinueve. Dicho abreviadamente debes “pasar” el diecinueve, que en el primer miembro está multiplicando, al segundo miembro de la igualdad dividiendo.

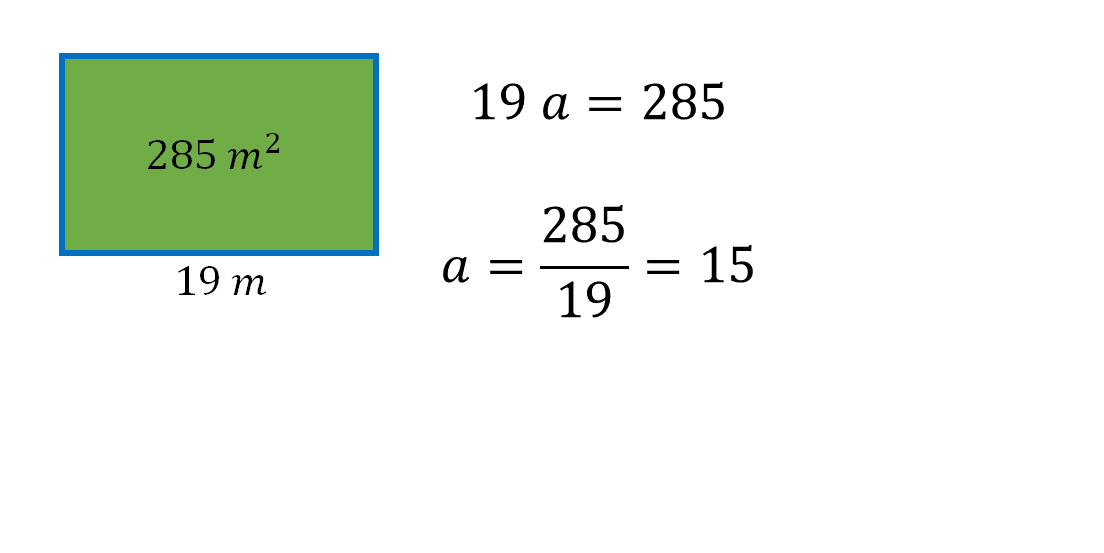
De esta manera, tienes que la medida del ancho del terreno representado por la incógnita “a”, es de quince metros.

Estás cerca de resolver el problema, ahora sólo debes calcular el perímetro del terreno, pues es la medida de la longitud de la barda.

El perímetro se calcula sumando todos los lados del terreno, en este caso:

La medida de la longitud de la barda es de sesenta y ocho metros.

Utilizar las propiedades de la igualdad ayuda a resolver ecuaciones. Identifícalo con la siguiente situación problemática.

Situación-problema, Grados

Pablo trabaja en el departamento de alimentos de un supermercado, le han explicado que para que la carne se conserve en buen estado, debe mantenerse en refrigeración, a una temperatura de entre cuatro y siete grados centígrados. Sin embargo, observa que el selector de temperatura en la cámara de refrigeración, indica la temperatura en grados Fahrenheit.

¿A qué temperatura en grados Fahrenheit debe colocar Pablo el selector, para mantener la carne en buen estado?

Pablo observa que, en el instructivo de la cámara de refrigeración, se encuentra una nota con la siguiente expresión: grados centígrados es igual a la diferencia de la temperatura expresada en grados Fahrenheit menos treinta y dos, multiplicado por cinco y dividido entre nueve, la cual permite encontrar la temperatura en grados centígrados, a partir del valor de la temperatura en grados Fahrenheit.

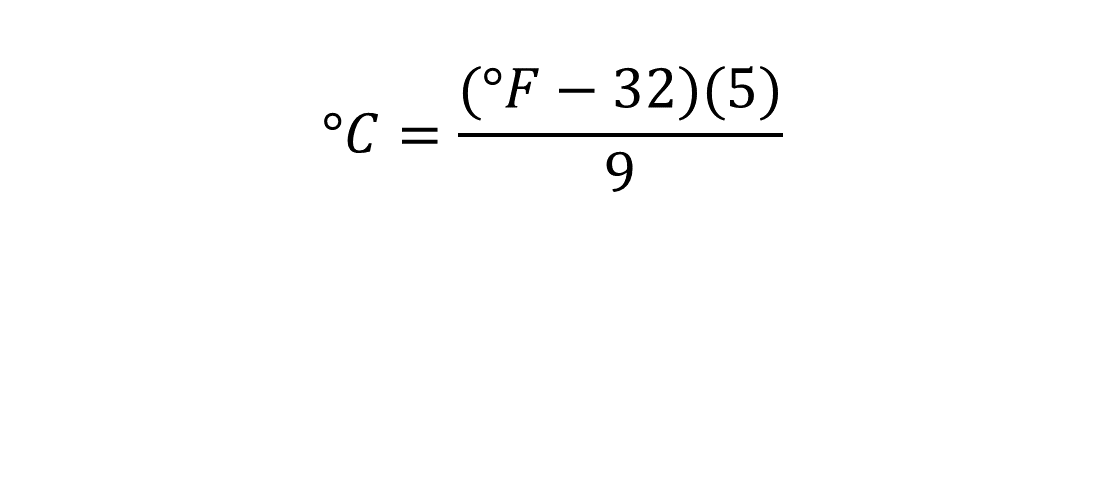
Pablo puede utilizarla para encontrar la equivalencia de grados Fahrenheit a grados centígrados, sólo debe dejar sola la variable grados Fahrenheit.

Para resolver esta situación, Pablo sabe que puede echar mano de lo que ha aprendido en sus clases de matemáticas con relación a las propiedades de la igualdad, y decide aplicarlas para encontrar la equivalencia de grados Fahrenheit, conociendo los grados centígrados.

Como se puede ver, la variable que se desea despejar es grados Fahrenheit, que se encuentra en el segundo miembro de la igualdad, por lo que se aplica la propiedad simétrica para establecerla en el primer miembro de la igualdad.

En la fórmula anterior, se puede observar que está siendo afectada por el número nueve, que está dividiendo, por lo que, para suprimirlo del primer miembro, lo “pasamos al segundo miembro” realizando la operación inversa a la división, que es la multiplicación.

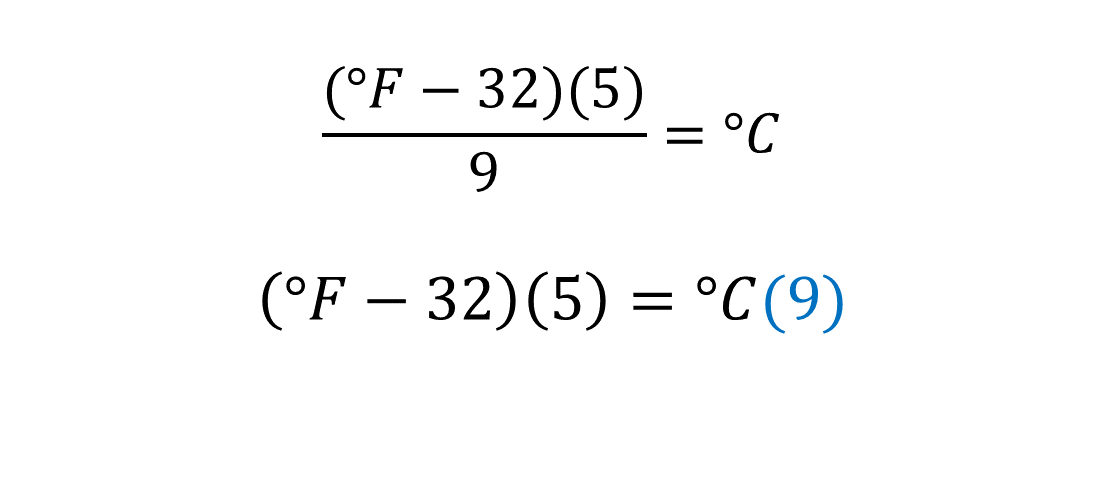
Tienes ahora la expresión que representa la resta grados Fahrenheit menos treinta y dos, afectada por el factor cinco, es igual a los grados centígrados, afectados por el factor nueve.

Para suprimir del primer miembro de la igualdad el factor cinco, aplicando la propiedad uniforme y las operaciones inversas, se tiene que, el factor cinco, pasa al segundo miembro de la igualdad dividiendo.

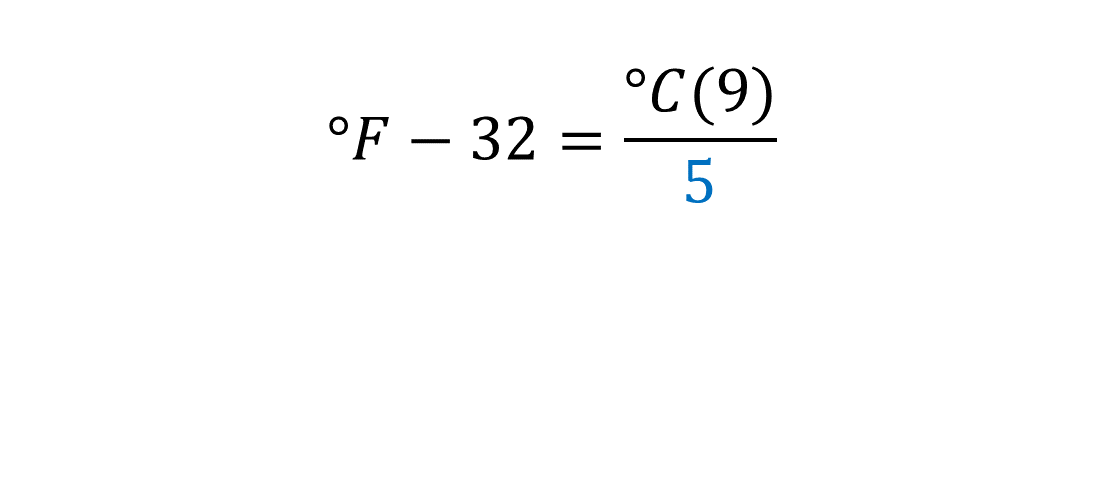
Ahora tienes la expresión grados Fahrenheit menos treinta y dos, es igual a grados centígrados por el factor nueve, sobre cinco.

Observa que el término que representa los grados Fahrenheit aun está afectado en el primer miembro por el número treinta y dos que se está restando.

Para quitarlo del primer miembro, lo cambias al segundo miembro con la operación contraria, sumando.

Ahora la expresión resultante es: grados Fahrenheit es igual a los grados Centígrados multiplicados por nueve y divididos por cinco, y a dicho resultado se le suma treinta y dos.

Utilizando esta relación, Raúl podrá calcular la equivalencia en grados Fahrenheit de una temperatura expresada en grados Centígrados para seleccionar la temperatura adecuada y conservar en buen estado el producto cárnico del supermercado.

Retomando la pregunta inicial, ¿a qué temperatura en grados Fahrenheit debe colocar Pablo el selector, para mantener la carne en buen estado?

Debes sustituir los valores cuatro y siete grados centígrados, uno a la vez, para conocer el rango de temperatura que Raúl debe seleccionar.

Realiza los cálculos en casa.

La reflexión y utilidad de los aprendizajes que adquieras en esta y otras asignaturas, sin duda te serán de ayuda para resolver alguna problemática que se te presente.

En esta sesión te enfocaste en identificar las propiedades de la igualdad; como la propiedad uniforme, la propiedad cancelativa y la propiedad simétrica; y las aplicaste.

El reto de hoy:

Busca en tu libro de texto el material que corresponde a esta sesión, y resuelve lo que se plantea, con la información que aquí estudiaste.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/

Descarga tu clase dando clic aquí