Producto de potencias de la misma base
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:07
Producto de potencias de la misma base
Aprendizaje esperado: resuelve problemas de potencias con exponente entero y aproxima raíces cuadradas.
Énfasis: elaborar, utilizar y justificar procedimientos para calcular productos de potencias enteras de la misma base.
¿Qué vamos a aprender?
En el libro “Álgebra recreativa”, del autor Yakov Perelmán, dice que con frecuencia se denomina al álgebra la «aritmética de las siete operaciones», y en ese sentido, hasta el momento has estudiado 4 operaciones: adición, sustracción, multiplicación y división con diferentes tipos de números y expresiones algebraicas.
En esta sesión, iniciarás con el estudio de la quinta operación matemática: la elevación a potencias. Para ello, analizarás diferentes planteamientos con la finalidad de construir un sentido y significado sobre el producto de potencias de la misma base.
¿Qué hacemos?
Para comenzar, analiza la siguiente situación.
Situación-problema, galletas en repisas
Sandra y Luis hornean galletas para vender y en cada paquete ponen cinco galletas. Cuentan con un anaquel con cinco repisas, para la exhibición y venta del producto, deciden acomodar los paquetes en cada repisa con cinco filas de cinco paquetes cada una.
De acuerdo con el planteamiento:
- ¿Cuántas galletas se exhiben en cada repisa?
- ¿Cuántas galletas hay en total para la venta?
- ¿Cómo se representaría la situación anterior?
Analiza las preguntas y busca responderlas.
Para obtener la cantidad de galletas por fila se multiplica: cinco galletas por cinco paquetes, es decir: 5 x 5
Cada repisa tiene cinco filas, por lo que se multiplica: 5 x 5 x 5. Si se realiza la operación, el producto es 125. Es decir, en cada repisa hay 125 galletas, con ello se ha dado respuesta a la primera pregunta.
Para saber cuántas galletas hay en total para la venta, considera que hay cinco repisas. Para obtener el total realiza la operación:
125 x 5 = 625
En total son 625 galletas para la venta.
Y, para responder la tercera pregunta:
¿Cómo se representaría la situación anterior?
Se puede decir que los datos se han representado a través de multiplicaciones.
Reflexiona:
¿Cómo se puede representar la o las operaciones anteriores de manera abreviada?
Considera que los elementos de la multiplicación son los factores, que son los números que se multiplican. Y el producto es el resultado de la multiplicación.
625 = 5 x 125
125 = 5 x 5 x 5
625 = 5 x 5 x 5 x 5
En esta multiplicación los factores son iguales, la multiplicación la puedes expresar de manera abreviada, como una potencia, en donde:
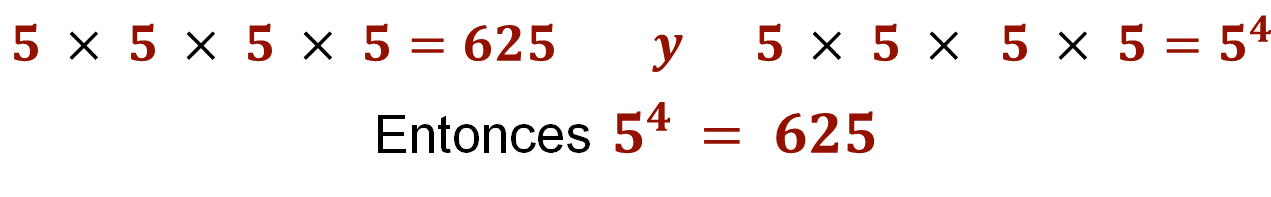
En el cual el número cuatro representa el número de veces que se multiplica a 5 por sí mismo.
Considera que al escribir en forma abreviada las multiplicaciones con factores iguales, al número que se repite como factor se le llama base. Y el número que se escribe arriba y a la derecha de la base se llama exponente.
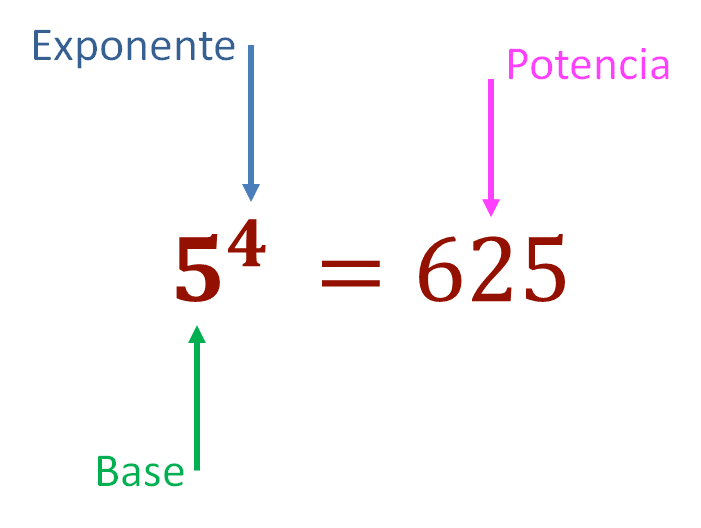
De la expresión cinco elevado al exponente cuatro, el número cinco corresponde a la base porque es el factor que se repite, cuatro es el exponente, indica que la base se multiplica cuatro veces por sí misma y seiscientos veinticinco es la potencia.
Continúa con el tema de los productos de las potencias con una misma base. Ahora resolverás el siguiente planteamiento.
Situación, carpintero
Un carpintero tiene que cortar piezas de madera de forma cuadrada con diferentes medidas. Necesita programar la máquina para realizar los cortes, para ello requiere una expresión que permita programar la máquina.

Se sabe que el área de un cuadrado se calcula multiplicando lado por lado, en este caso se utiliza una literal que permite representar la medida de cada lado que es variable. La expresión es:
Área = b x b
¿Cómo expresarías de manera abreviada la multiplicación?
Como ya has analizado, tienes una situación similar a la del problema anterior; es decir, se cuenta con un factor que se repite, en este caso b.
Esta literal es la base, y para indicar que se repite dos veces la multiplicación, anota como exponente el número dos, es decir:
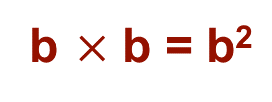
Así, el área es igual a “b” elevada al exponente dos. Esta es la expresión que permitirá al carpintero programar la máquina. Al tener la expresión, “b” al cuadrado, te puedes dar cuenta de que también las literales pueden expresarse como potencia.
Ahora resuelve otro problema utilizando el volumen de un cubo como referencia.
Situación-problema, cubo
Para calcular el volumen de un cubo, como el que se muestra en la siguiente imagen, se necesita aplicar la fórmula correspondiente. La medida de cada arista está representada con la literal “a”. El volumen se obtiene multiplicando las tres dimensiones del cuerpo geométrico.
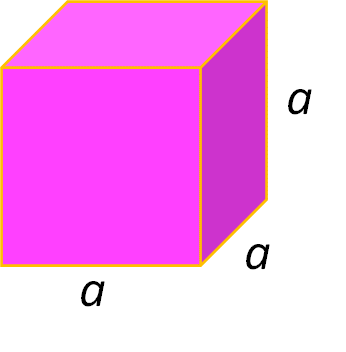
La fórmula para obtener el volumen de un cubo es arista por arista por arista. Aplicando los conocimientos aprendidos tienes que esta expresión puede representarse de manera abreviada; es decir: a x a x a, lo que es igual a la literal a elevada al exponente tres. Entonces el volumen es igual a “a” elevada al exponente tres.
Es importante que consideres que la operación de multiplicación se puede representar de la siguiente manera:
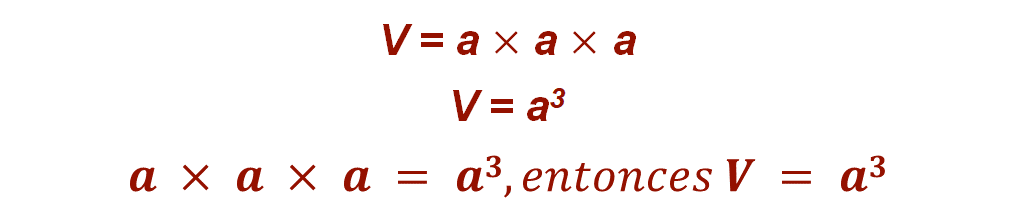
Reflexiona acerca de la forma general para representar el producto de factores iguales, ya sean números o literales. La forma general es:
“a” elevado al exponente “n”, donde “a” corresponde a la base y “n” se refiere al exponente.
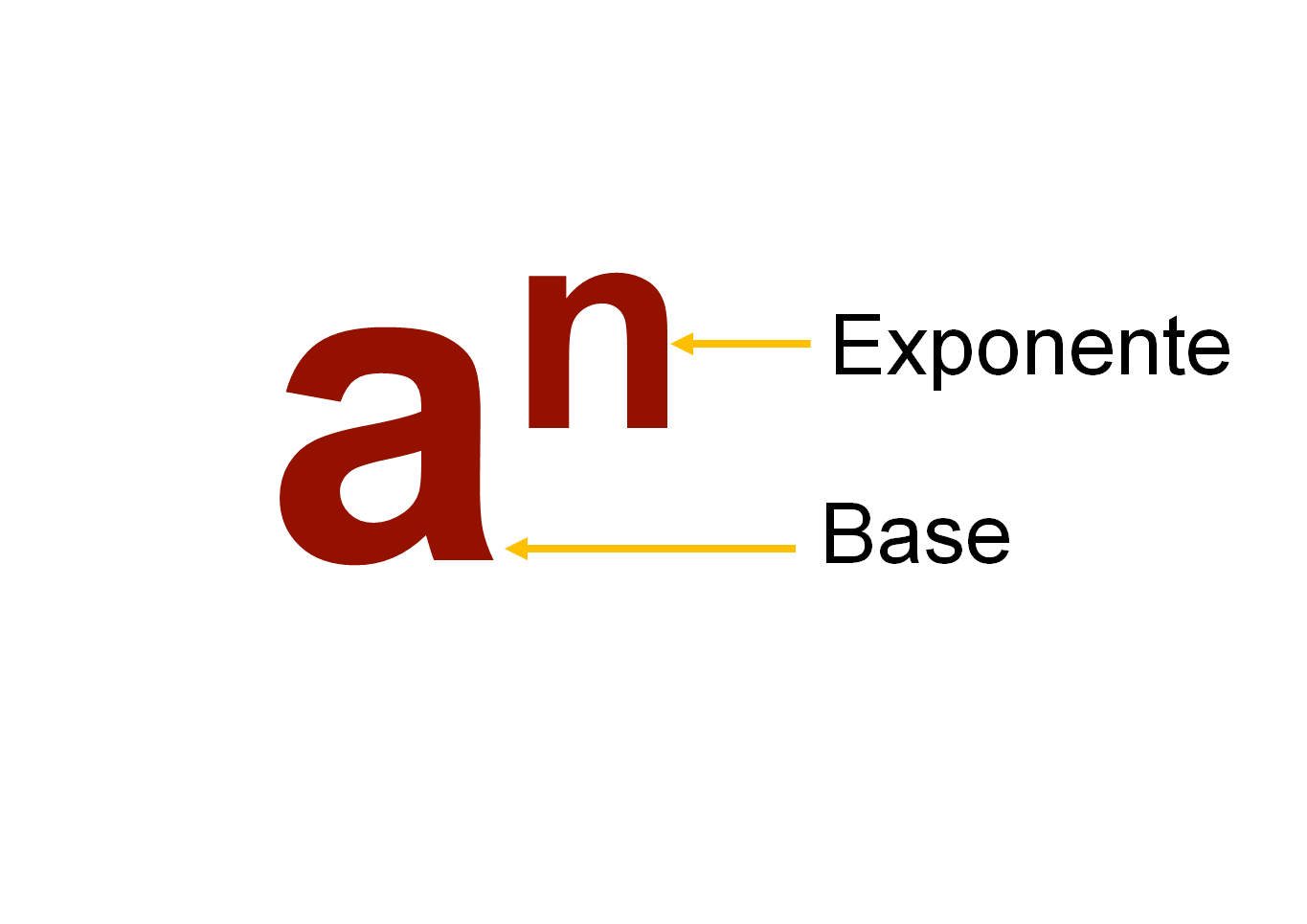
Todo número elevado a un exponente implica la multiplicación de la base tantas veces como indica el exponente, siempre y cuando “n” sea un entero positivo.
Para aplicar lo aprendido, reflexiona acerca del cálculo del volumen de un paralelepípedo, en este caso una caja de cartón.
Situación, caja de cartón
Observa la siguiente imagen. Cuentas con las medidas de cada una de las dimensiones de la caja de cartón que corresponde a un prisma rectangular.

Las dimensiones de la base son:
Largo: 3 x 3 x 3 x 3 x 3
Ancho: 3 x 3
La altura del prisma: 3 x 3 x 3
¿Cómo se calcula el volumen?
Para calcular el volumen del prisma de base rectangular necesitas multiplicar las tres dimensiones: largo, ancho y altura.
Al utilizar lo que acabas de aprender, identificarás que el largo de la base se expresa de la siguiente manera:

El ancho de la base se expresa:
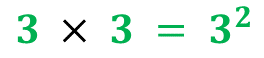
La altura del prisma la puedes escribir de la siguiente forma:

Aplicando la fórmula para calcular el volumen tienes dos formas de representarla:

Al expresar lo anterior de forma abreviada tienes que:
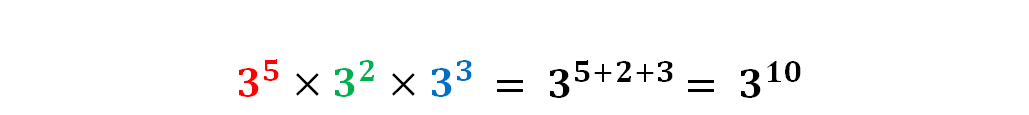
Como te habrás dado cuenta, la operación anterior corresponde a una multiplicación de potencias con la misma base, para obtener el resultado se sumaron los exponentes.
Por lo tanto, obtuviste el mismo resultado de la operación que realizaste de forma desarrollada.
Como conclusión, se puede decir que: cuando se multiplican dos o más potencias de la misma base, el resultado es una potencia con la misma base y el exponente es la suma de los exponentes de los factores. Para expresarlo de manera general tienes lo siguiente:
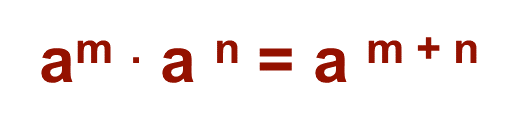
Donde “m” y “n” representan números enteros positivos.
A continuación, aplica lo aprendido y resuelve lo siguiente.
Utiliza la regla de la multiplicación de potencias con la misma base para resolver lo siguiente:
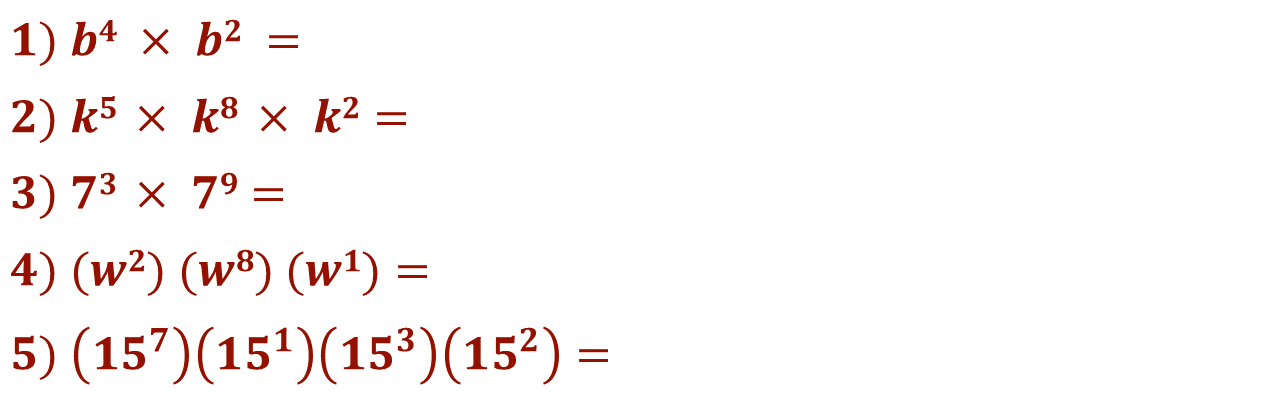
Aunque el exponente uno en una potencia generalmente se omite, en este caso, lo anotarás para que lo tengas presente.
Después de resolver lo anterior, verifica tus respuestas.
Para el inciso 1, se identifica que tiene la misma base, “b” y los exponentes 4 y 2 se suman. El resultado es:

En el inciso 2 tienes la misma base, que es “k”. Realiza la suma de los exponentes de los factores; en este caso, 5 más 8 más 2. Por lo tanto:

En el inciso 3 tienes la misma base, que es 7. Realiza la suma de los exponentes de los factores; en este caso, 3 más 9:

En el inciso 4, la base es “w” y los exponentes de los factores se suman, es decir, 2 más 8 más 1:

En el último inciso (5) tienes cuatro factores con la misma base. Procede de la misma manera, 15 es la base de la potencia y el exponente lo obtienes sumando 7 más 1 más 3 más 2:

Es importante que anotes las operaciones y trates de resolverlas con el conocimiento que vayas adquiriendo a lo largo de la sesión. Ahora presta atención al siguiente planteamiento.
Reflexiona acerca de situaciones como la siguiente:
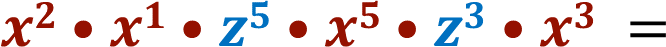
¿Puedes sumar los exponentes de las “x” y las “z”?
No, la regla sólo aplica a potencias con la misma base, y en este caso, tienes a factores con bases distintas.
En color rojo se identifican las potencias cuya base es “x”, y con azul las potencias cuya base es “z”. El producto indica que “x” está elevada al exponente 11, y “z” elevada al exponente 8; a estos factores no se les aplica la regla debido a que no tienen la misma base, entonces se deja expresado el producto.
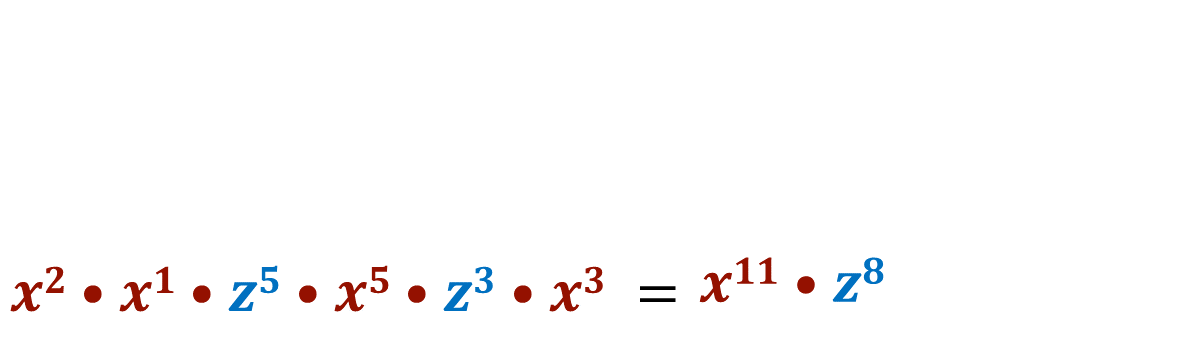
La potencia resultante es “x” elevada al exponente once por “z” elevada al exponente ocho.
Después de la información anterior, resuelve los siguientes productos:
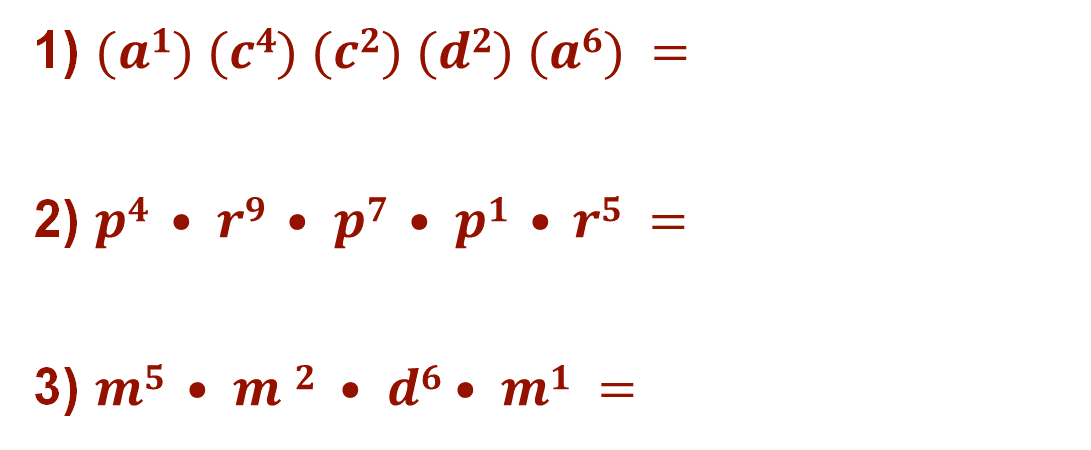
Para el inciso 1, debes identificar aquellos factores con la misma base, de preferencia en orden alfabético; sin embargo, no debes olvidar la propiedad conmutativa de la multiplicación que dice: en una multiplicación, el orden de los factores no altera el producto.
Si comienzas con la literal “a” tienes que sólo dos factores tienen la misma base, “a” elevada a la 1 y “a” elevada a la 6; es decir, el resultado del primer producto será “a” elevada a la uno más seis, de manera abreviada resulta “a” elevada a la séptima potencia.
Para la literal “c” tienes dos factores cuyos exponentes son 4 y 2, de esta manera, al operar estos factores obtienes la potencia “c” elevada al exponente 6.
Queda un solo factor: d elevada a la 2, como no hay otro factor o factores con la misma base lo recorres al resultado.
Para finalizar el ejercicio anota el resultado que es: “a” elevada a la 7, por “c” a la 6 por “d” cuadrada.
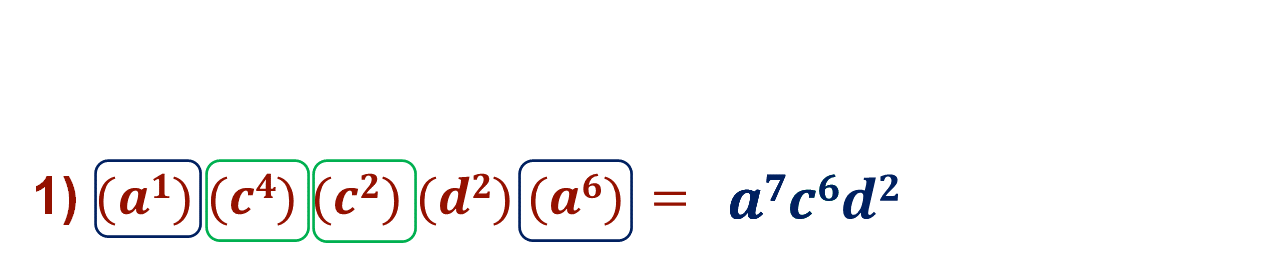
Recuerda que para representar la multiplicación puedes usar un punto, el signo (x), o bien, paréntesis; en el caso de las literales no es necesario representar el signo de multiplicación, es decir, dos o más literales juntas implican una multiplicación.
Continúa con el siguiente producto.
En el inciso 2, los factores cuya base es “p” tienen los exponentes 4, 7 y 1. Por lo tanto, se suman para poder expresar la potencia, la cual queda como “p” elevada a la 12. Los otros factores que tienen la misma base son “r” elevado al exponente 9 y “r” elevado al exponente 5, de manera abreviada se tiene “r” elevado al exponente 14.
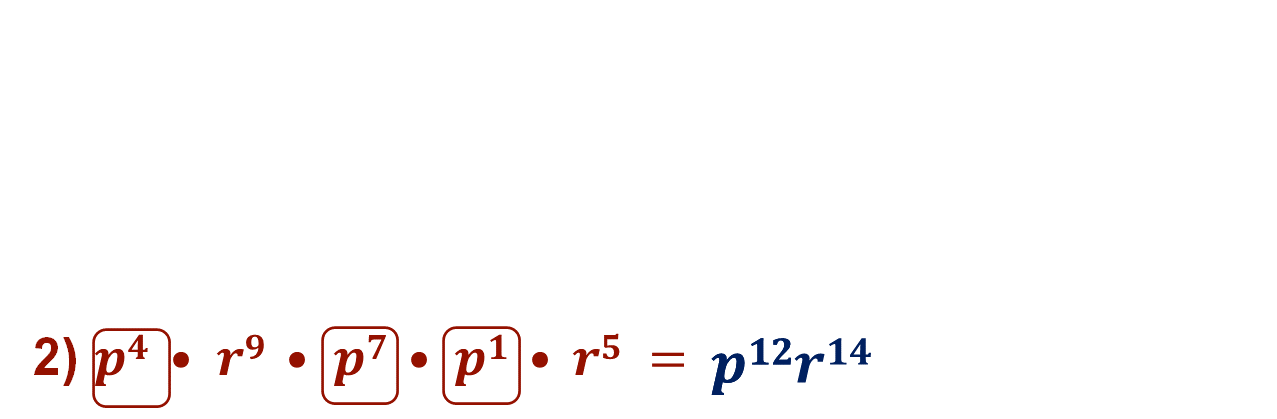
El resultado final es “p” elevado al exponente 12 por “r” elevado al exponente 14.
En el inciso 3, para multiplicar los factores que tienen como base la literal “m”, suma sus exponentes 5 + 2 + 1 y el resultado es “m” a la 8. Luego, se tiene a la literal “d”, que es el único factor con esa base, lo anotas en el resultado, con el mismo exponente.
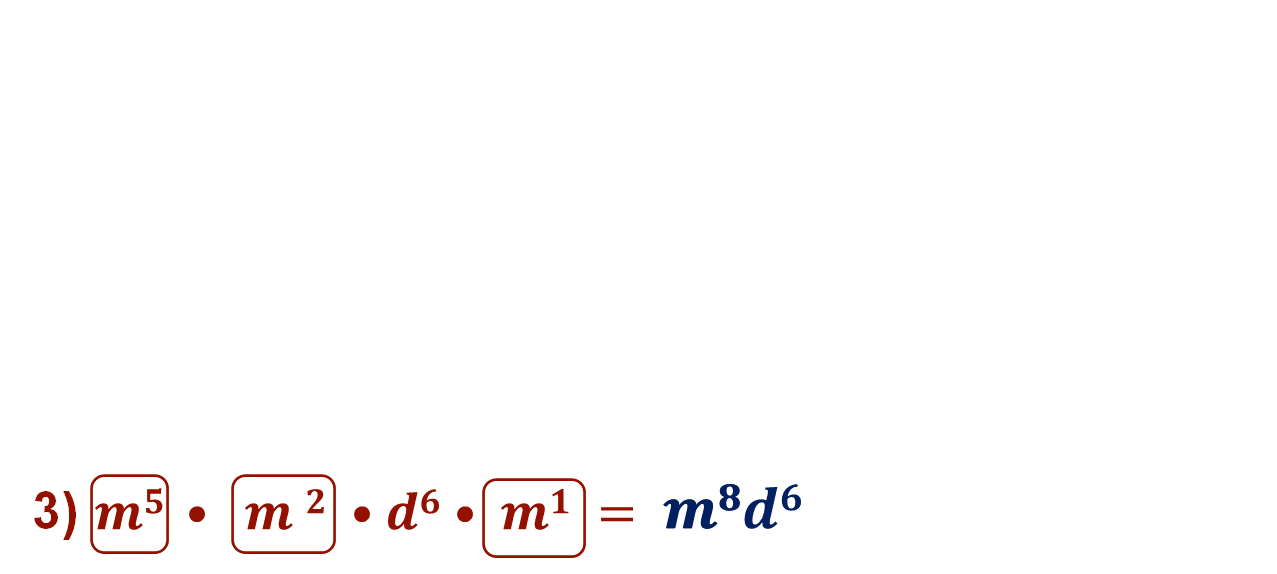
El resultado final es el producto m elevado al exponente ocho y d elevado al exponente seis.
Para concluir esta sesión, resuelve un último problema.
Situación-problema, amibas
Las amibas son protozoos que habitan en la tierra y el agua, se reproducen dividiéndose por la mitad, a este proceso se le conoce como bipartición.
Adrián realiza cultivos en un laboratorio. Suponiendo que se reproducen aproximadamente cada dos días, realiza lo que se solicita.
- Calcula cuántas amibas habrá después de 4 y 12 días.
- Si Adrián contabiliza quinientas doce amibas, ¿cuántos días habrán transcurrido?
- Escribe una expresión que generalice la situación anterior.
Para contestar las preguntas puedes utilizar una tabla con cuatro columnas para representar la bipartición de las amibas cada dos días.
- En la primera columna se anotan los días que han transcurrido; como la bipartición es cada dos días anota los números a partir de la segunda fila, serían dos, cuatro, seis; y así sucesivamente, hasta el número veinte.
- En la segunda columna, anota los periodos de bipartición, como se registró desde el inicio, comienza en el periodo de bipartición cero.
- En la tercera columna anota la operación que permite determinar el número de amibas a través de los periodos de bipartición.
- En la cuarta columna se anota el número de amibas de acuerdo con el número de días que han transcurrido desde el inicio o de acuerdo con el periodo de bipartición.
Observa cómo quedaría la tabla.
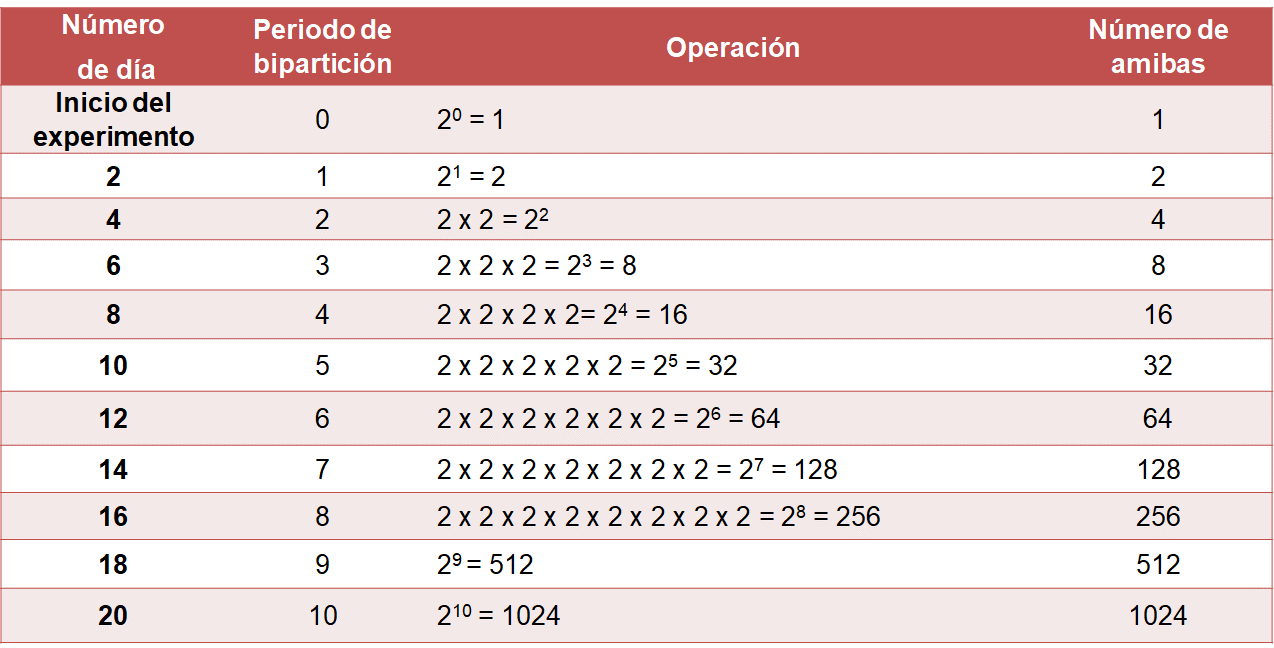
En la primera fila están los datos desde que comenzó el experimento. Por lo tanto, el periodo de bipartición es cero, en la tercera columna se tiene el número uno, refiriendo a que se comenzó con una amiba, y este dato se repite en la cuarta columna.
Para la segunda fila se tiene que ya han transcurrido dos días, eso implica el primer periodo de bipartición; por lo tanto, en la tercera columna, donde se indican las operaciones, se tendrá uno por 2, es decir, una amiba que tuvo bipartición; así, después de dos días se tendrán dos amibas.
En la tercera fila ya han transcurrido cuatro días, es decir, dos periodos, entonces cada una de las dos amibas se multiplicaron por dos, esto se representa en la tercera columna como dos por dos. Si se expresa de manera abreviada, se tiene: dos elevado al exponente dos, que equivale a 4, es decir, 4 amibas, dato que corresponde a la cuarta columna.
La cuarta fila corresponde a seis días transcurridos, es decir, tres periodos de bipartición, lo que se representa como: dos por dos por dos; expresión equivalente a dos elevado al cubo, que es igual a ocho, es decir, ocho amibas corresponden a la cuarta columna.
La fila cinco corresponde el día ocho; es decir, el periodo cuatro de bipartición. Para representarlo se tiene que es dos por dos por dos por dos, y para abreviarlo se anota: dos elevado a la cuarta potencia. Al resolver la potencia es igual a dieciséis, es decir, habrá 16 amibas.
En la fila seis se tiene el quinto periodo de bipartición y se representa como dos por dos por dos por dos por dos, que equivale a decir dos elevado a la quinta potencia, que es igual a 32 amibas.
La fila siete corresponde al periodo seis de bipartición, esto significa dos por dos por dos por dos por dos por dos, es lo mismo que anotar dos elevado a la sexta potencia. Al realizar la operación se obtiene 64, es decir, sesenta y cuatro amibas.
Se continúa con el mismo procedimiento hasta completar los datos de la tabla. En el periodo siete se sabe que la operación es dos elevado al exponente siete y es igual a ciento veintiocho, es decir, ciento veintiocho amibas.
Para el periodo de bipartición ocho se tiene la operación dos elevado a la ocho, que es igual a doscientas cincuenta y seis amibas.
En el periodo nueve la operación a realizar es dos elevado al exponente nueve que es igual a quinientas doce amibas.
De igual manera, para el periodo diez se anota dos elevado al exponente diez, que es igual a mil veinticuatro amibas.
Ahora, para dar respuesta a las preguntas, utiliza los datos obtenidos en la tabla.
Para el inciso “a”:
¿Cuántas amibas habrá después de 4 y 12 días?
Se tiene que después de cuatro días habrá cuatro amibas y después de doce días habrá sesenta y cuatro amibas.
Para resolver el inciso b:
Si Adrián contabiliza quinientas doce amibas, ¿cuántos días habrán transcurrido?
Puedes verificar la tabla y decir que cuando haya 512 amibas habrán transcurrido 18 días.
Finalmente, para encontrar una expresión que generalice el crecimiento de la población de amibas durante los periodos de reproducción, el factor que se repite en las operaciones de la tercera columna, es el número dos, este número corresponde a la base de la potencia.
El exponente corresponde al periodo de bipartición, como este número va cambiando, se puede representar con una letra, en este caso, será la letra “n” para indicar el dato variable. Así se obtiene la expresión general que es dos elevado a la potencia “n”, donde “n” representa el periodo de bipartición, al hacer la operación se encuentra el número de amibas.
Con la actividad anterior has finalizado esta sesión, en la que estudiaste el tema: producto de potencias de la misma base.
Es importante que tengas presente que las actividades que realizaste corresponden a un material de apoyo, y puedes fortalecer lo aprendido resolviendo las actividades del libro de texto de Matemáticas de segundo grado.
El reto de hoy:
Expresa de manera abreviada las siguientes multiplicaciones:
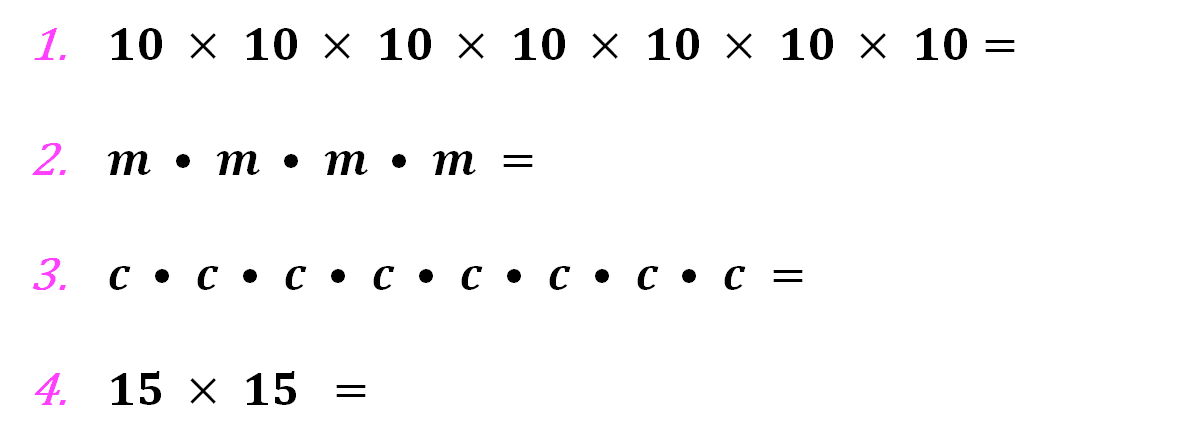
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/





Login to join the discussion