Problemas aditivos con números fraccionarios I
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 16:42Aprendizaje esperado: resolución de problemas aditivos con números naturales, decimales y fraccionarios, variando la estructura de los problemas. Estudio o reafirmación de los algoritmos convencionales.
Énfasis: resolver problemas aditivos con números fraccionarios que tienen diferente denominador.
¿Qué vamos a aprender?
Aprenderás a resolver problemas aditivos con números naturales, decimales y fraccionarios, variando la estructura de los problemas. Estudio o reafirmación de los algoritmos convencionales.
Para explorar más puedes revisar el libro de texto de Desafíos matemáticos de 6º, se explica el tema a partir de la página 15.
https://libros.conaliteg.gob.mx/20/P6DMA.htm#page/15
¿Qué hacemos?
Analiza la información y algunas actividades que te ayudarán a resuelver problemas aditivos con números fraccionarios que tienen diferente denominador.
Aprenderás información que se requiere para poder resolver el primer problema del desafío 6 de nuestro libro de texto.
Seguramente en alguna ocasión has ido a comprar ¼ kg de queso o ¼ kg de jamón, ½ kg de huevo y varios alimentos mas.
Esas cantidades, se llaman fracciones.
¿Qué son las fracciones?
Se podría decir que son partes iguales en las que se dividen los enteros, pero mejor, presta atención:
Observa qué son las fracciones, pero no sólo desde un punto de vista real, sino desde el punto de vista de los números, lo cual te ayudará a entender las operaciones con fracciones.
Una definición dice que las fracciones son una forma de representar las partes de un todo. Por ejemplo, tenemos esta barra rectangular.

Podríamos dividirla en 2 partes iguales.

La parte que está coloreada de verde, se representa como una fracción de esta forma:
Donde el denominador, representa las partes totales en el que se ha dividido el todo.
El número de arriba, el numerador, representa las partes a la que queremos hacer referencia.
Puedes dividir el todo en la partes que queramos; eso sí, las partes tienen que ser iguales.
Ahora divide la barra en 3 partes iguales:

¿Cómo se representa en forma de fracción la parte pintada de verde?
Ahora en el denominador (el número de abajo) tenemos un 3, que son las partes en las que has dividido la barra y en el numerador (la parte de arriba) hay un 2, que son las partes pintadas de verde y a las que queremos hacer referencia.
Si la dividides en 4 partes y pintas sólo 1 parte de verde.
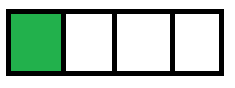
Esta parte se representaría:
Ahora bien, esta definición de qué son las fracciones sólo es válida si el número al que estas representando es menor que 1, ya que estas haciendo referencia a una o más partes del todo.
Sin embargo, también puedes representar en forma de fracción el todo completo, es decir, si divides la barra en 3 partes y quieres hacer referencia a las 3 partes.

Se representaría:
El numerador y el denominador son iguales, porque las partes en las que se divide la barra y a las que haces referencia son las mismas.
De hecho, si realizas la división, te da como resultado la unidad:
Las fracciones son otra forma de representar los números, tanto los decimales como los enteros. Es como dejar la división indicada sin llegar al resultado final.
En el último ejemplo, has representado las 3 partes que forman la barra completa, es decir, el todo. Si realizas la división, te da la unidad:
Las fracciones anteriores, también puedes expresarlas como números decimales si terminas de realizar la división:
Hasta ahora, el numerador siempre ha sido menor o igual que el denominador, pero ¿El numerador puede ser mayor que el denominador? Por supuesto que sí.
En ese caso, las fracciones ya no representan partes de un todo, sino un reparto o, mejor dicho, una división.
Ahora que ya tienes un poco más claro qué son las fracciones desde el punto de vista matemático, ve otro concepto: Las fracciones equivalentes.
Las fracciones equivalentes son aquellas que cuando las dividimos tienen el mismo valor o, dicho de otra forma, representan al mismo número (decimal o entero).
Ve a verlo más despacio con algunos ejemplos:
Tienes una barra dividida en 2 partes iguales y quieres representar en forma de fracción la parte coloreada de verde:

Las 2 partes en la que has dividido la barra serán el denominador y la parte de verde será el numerador:
Si realizas la división, la fracción tiene un valor de:
Ahora quieres representar la misma parte coloreada de verde, pero en este caso la barra estará dividida en 4 partes. Para que la parte de verde sea igual que la parte de verde del caso anterior, le corresponderán 2 partes de la barra.

Las 4 partes en la que has dividido la barra serán el denominador y las 2 partes de verde serán el numerador:
Y esta fracción tiene un valor de:
Como la parte de verde de ambos casos es igual, el valor de cada fracción es el mismo (no podía ser de otra forma). Por tanto, las fracciones:
Son fracciones equivalentes y son dos formas distintas de representar al mismo número.


De la misma forma, si queremos representar la unidad en forma de fracción, tienes infinitas formas de hacerlo, siempre y cuando el numerador y el denominador sean iguales; ejemplos:
 = 1
= 1
 = 1
= 1
 = 1
= 1
El valor de todas estas fracciones es 1
Por tanto, también son fracciones equivalentes y son distintas fracciones para representar una misma unidad.
Por último, es lo mismo repartir 10 unidades entre 4, que 5 unidades entre 2 o que 100 unidades entre 40. El resultado de todos los repartos es el mismo:
Ahora, el asunto es ¿Cómo obtienes fracciones equivalentes? Una forma es la siguiente:
Si tu unidad o entero está dividido en medios y cada fracción la vuelvo a dividir en partes iguales ¿Cuántas partes tienes ahora iluminadas?
| Fracción | Fracción equivalente |
=
¿Qué sucedió aquí?
El 2, que es el numerador, es el doble de 1 y el 4 es el doble de 2.
Seguramente tu ya sabes cómo puedes obtener entonces una fracción equivalente sin tener que dibujarla.
Observa lo que le sucede al numerador esto tiene que sucederle igual al denominador. El resultado es el doble, y una cantidad para que sea el doble puedes multiplicarla por dos. Ve si es verdad.
Muy bien. De esta manera puedes obtener fracciones equivalentes de todas las fracciones; recuerda que puedes multiplicar por cualquier número, la única regla es que lo que le pasa al numerador debe sucederle igual al denominador.
Actividad 1.
Es momento de trabajar con tu libro de texto, en el cual vas a aplicar lo que acabas de recordar.
Abre tu libro en el desafío 6, “Vamos a completar”, que se encuentra en la página 15. Resuelve la siguiente situación.
Para comprar un juego de mesa yo aporté un quinto del total del precio, mi hermana María la sexta parte y mi papá el resto. ¿Qué parte del costo del juego aportó mi papá, si pagamos $90? ¿Cuánto dinero puso cada uno?
Lectura del problema 1.
Observa. Es un problema que solicita dos repuestas, porque tiene dos preguntas.
Así que primero trata la respuesta a la primera pregunta: ¿Qué parte del costo del juego aportó mi papá?
Identifica ¿Cuál es la información que brinda el problema? ¿Qué es lo que la familia a decidido comprar? Bien. Un juego de mesa. ¿Cuánto cuesta el juego de mesa? $90 pesos. Excelente.
El problema dice que el gasto lo hicieron tres personas, pero cada una aportó cantidades diferentes.
Datos:
| Tú | MARÍA | PAPÁ | TOTAL |
| ? | 1 |
El total representa, la unidad, un entero, ahora sí, ¿Cómo haces para saber qué parte del entero aportó el papá?
Para encontrar la respuesta puedes seguir muchos caminos y cada uno puede encontrar uno diferente; para resolverlo, el proceso que tú encuentres quizá sea más fácil que el que vas a ver a continuación o, tal vez, será más fácil para otros, pero al final todos llegan al mismo resultado.
Necesitas juntar lo que tú aportaste y lo de María para saber cuánto del total o entero puso papá, y la oporación que harás es una suma, ¿Qué vaas a sumar?
=
¿Sabes cómo podem hacer la suma de fracciones? Para hacer una suma de fracciones, los denominadores deben ser iguales. ¿Cómo puedes hacer que tengan un denominador igual?
A través de una multiplicación. El mismo número que multiplica al numerador tiene que multiplicar al denominador.
Observa = tienes que buscar un mismo denominador.
5 x ___= ___ qué número daría el mismo resultado que 6 x ___=___
En el resultado los dos deben tener el mismo.
Puedes multiplicar 5 x 6 = 30 Ya que si multiplicas el 6 X 5 también nos da 30.
No olvides que lo mismo que le sucede al denominador le debe suceder al numerador, por lo tanto:
Las fracciones equivalentes quedarían así:
Ahora sí, como ya tienes denominadores iguales puedes realizar la suma.
Ahora, ¿Cómo le haces para saber cuánto puso el papá?
La parte que puso el papá es lo que falta para completar un entero. ¿Cómo lo haces?
Observa:
| TÚ | MARÍA | PAPÁ | TOTAL |
| ? | 1 |
Si estas hablado de 6/30 ¿Qué es lo que indica el denominador?
El denominador indica las partes en que está dividido un entero, o sea 30/30.
Esto significa que el entero está dividido en treintavos. Analiza: si tú pusiste 6/30 y María puso 5/30, ¿Cómo puedes calcular lo que puso el papá?
Observa la siguiente pista.
Lo que puso el papá es lo que falta, María y tú tienen:
El papá puso lo que falta para 30/30.
entonces ¿Cuánto falta para 30/30 si se tienen 11/30?
19/30
El papá puso 19/30 del costo del juego.
Ahora va a ser más fácil encontrar las respuestas que solicita la segunda pregunta:
¿Cuánto dinero puso cada uno?
Recuerda los datos:
| Tú | MARÍA | PAPÁ | TOTAL |
| 1 |
O puedes usar esta información que obtuviste al buscar fracciones equivalentes:
Al observar las tablas, ¿Crees que tienen información que ayude a saber cuánto dinero aportó cada uno para comprar el juego?
Analiza. el juego: Costó $90 pesos. Cada uno de los integrantes puso una parte.
Retomando las fracciones equivalentes que puedes afirmar que el entero esta dividido en 30/30, de los cuales tú pusiste 6/30, María puso 5/30 y el papá 19/30.
Pero, ¿Cómo encontrar lo equivalente o la parte en dinero que puso cada uno?
Si el entero se divide en treinta parte iguales, entonces hay que calcular cuánto dinero representa un treintavo de 90 pesos. Una forma es dividir $90 pesos entre treinta.
Divide 90 entre 30.
Necesitas saber cuánto dinero equivale un treintavo (1/30), para poder saber cuánto puso cada quien.
Divide
$90 entre 30 y nos da 3 pesos
Eso significa que 1/30 representa 3 pesos, por lo tanto ya puedes saber cuánto dinero puso cada quien. Si tú pusiste 6 partes de 30, y cada parte es lo mismo que 3 pesos, entonces es posible multiplicar 6 X 3 = $ 18 pesos, 5 partes X tres pesos = $15 pesos y 19 partes por $3 pesos= $ 57 pesos
| TÚ | MARÍA | PAPÁ | TOTAL |
|
|
|||
| $18 | $15 | $57 | $90 |
Como te diste cuenta, al usar fracciones equivalentes pudiste realizar la suma de fracciones que necesitabas para encontrar la respuesta a la primera pregunta. Con los datos que calculaste del primer problema pudiste llegar más rápido al resultado de la segunda pregunta.
El reto de hoy:
Revisa lo que trabajaste, porque continuaras trabajando dos sesiones más con el uso de fracciones en sus diferentes expresiones.
Si en tu casa hay libros relacionados con el tema, consúltalos. Así podrás saber más. Si no cuentas con estos materiales no te preocupes. En cualquier caso, platica con tu familia sobre lo que aprendiste, seguro les parecerá interesante.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas





Login to join the discussion