Probabilidad y juegos
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:24
Probabilidad y juegos
Aprendizaje esperado: compara la tendencia central (media, mediana y moda) y dispersión (rango y desviación media) de dos conjuntos de datos.
Énfasis: analizar las condiciones necesarias para que un juego de azar sea justo.
¿Qué vamos a aprender?
Los materiales que requerirás son tu cuaderno de apuntes, hojas blancas, lápiz y goma.
En los juegos de azar las posibilidades de ganar o perder están determinadas por la probabilidad de ocurrencia de los eventos favorables y conociste algunos juegos de azar clásicos.
En los siguientes casos determina si las condiciones o reglas permiten que sean juegos de azar justos o de resultados equiprobables.
Rifa: Ganar el premio al comprar tres boletos de 500 posibles.

Lotería instantánea o rapadito: Ganar el premio si raspas consecutivamente tres figuras iguales.

Lanzar un dado: Ganar si sale un número menor que 3.

Ruleta: Ganar un premio al girarla.

Lotería mexicana: Ganar en la primera jugada.

Volados: Ganar si sale sol.

Cuando se participa en juegos de azar y se pierde, por lo general se tiene la sensación de que se está en desventaja o, por el contrario, que el juego no es justo.
¿Alguna vez te has preguntado si las reglas de un juego son justas?
Estudiarás las condiciones necesarias para garantizar que, en un juego de azar, los jugadores tengan la misma probabilidad de ganar.
¿Qué hacemos?
Parte de un ejemplo clásico y sencillo, que te ayudará a identificar de qué se trata el estudio.
Se tiene una moneda cuyas caras son 0 y 1. Por lo tanto, al lanzar una de estas monedas, existe la posibilidad de que caiga 0 o 1, es decir, gane Persona 1 o Persona 2.
Se determina que cuando caiga cero, gana Persona 1 y cuando caiga uno, Persona 2 gana. El juego parece justo, ya que cada uno tiene la misma posibilidad de ganar.
Al ser dos los resultados posibles y asignar un resultado para cada uno de los dos, se puede decir que “está parejo el juego”, o lo que se entiende como “un juego justo”.
Conoce una variante del mismo ejemplo para conocer cómo se modifican las condiciones del juego.
Se realiza el juego con dos monedas para lanzarse de tal manera que, si al caer las dos monedas, sus caras suman cero, gana Persona 1.
Caso contrario, si la suma de las dos monedas es 1, gana Persona 2. Y si la suma de las dos monedas es igual a dos, nadie gana.
Pero ¿Se precisa que el juego sea justo?
Para saberlo, se analiza si en realidad es un juego en donde se tienen las mismas probabilidades de ganar.

Estos resultados se concentran en una tabla de doble entrada: El cero y el uno del primer renglón son los posibles resultados para la moneda uno, y los resultados de la primera columna son para la moneda dos.
Los cuadros en donde se cruzan los resultados de cada moneda corresponden a la suma de los resultados, de tal manera que cero más cero es cero; con este resultado gana Persona 1.
En el segundo cuadro, cero más uno es uno; en el tercer cuadro, uno más cero, el resultado también es 1, que es el resultado con el que gana Persona 2.
También se sabe que cuando ambas monedas caen en uno, el resultado es 2; una situación en la que nadie gana.
De las cuatro probabilidades que hay para las dos monedas, una hace ganar a la Persona 1, dos hacen ganar a Persona 2 y en una, nadie gana.
De este modo, Persona 2 se tiene el doble de posibilidades de ganar y eso no es justo para la Persona 1.
Lo que se necesita para que un juego sea justo, es que las probabilidades sean las mismas para todos los jugadores. Cuando esto ocurre, se dice que los “resultados son equiprobables”, como en el primer ejemplo que se citó, en el que los resultados son iguales para ambos.
Cuando las probabilidades para todos los jugadores son diferentes, se dice que los resultados son “no equiprobables”, como en el segundo ejemplo, en donde los resultados no son iguales para ambos.
Es así como el juego planteado no es justo, porque existe una probabilidad mayor de las otras dos, por lo que el reordenar la forma en que ganaría la Persona 1 o la Persona 2, tampoco mejoraría la situación. Es decir, no es justo porque la probabilidad basada en la suma de los resultados de las monedas no es equiprobable.
Para hacer del juego justo, se deben cambiar las condiciones. Así, si cambia que el maestro Marcial gana al obtener caras iguales en las dos monedas —y yo gano si caen diferentes caras en el lanzamiento de las dos monedas—, ambos tenemos la misma posibilidad de ganar.
Si se observa la tabla con las posibles combinaciones, al lanzar las dos monedas se encuentra que:
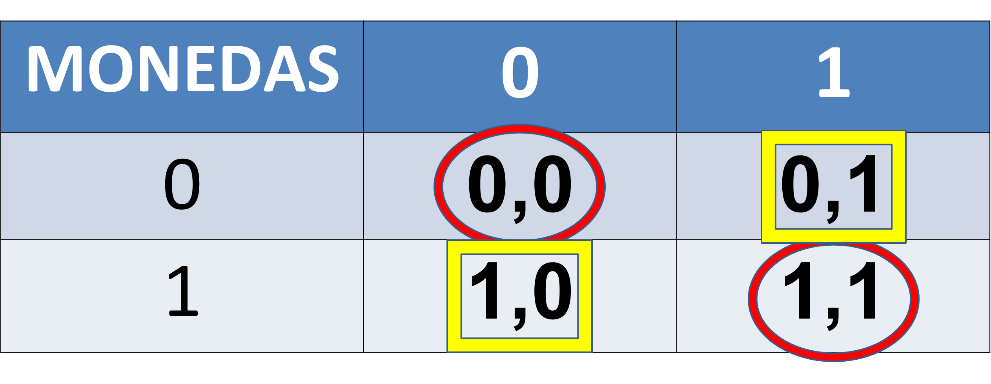
Existen dos opciones en donde las caras de las monedas son iguales.
Sin embargo, hay otras dos opciones en donde las caras de las monedas son diferentes: Son dos posibilidades para cada uno por ganar, lo que hace equiprobable el resultado.
En estas dos situaciones, se distinguió que para que un juego sea justo, requiere de resultados equiprobables. Y que cuando se tienen resultados no equiprobables, por ende, el juego es injusto.
Para comprenderlo mejor, se estudia otra situación en la que se evalúan los resultados de un juego, a saber, si es justo.
Se tienen un par de dados y tres fichas pequeñas. El juego lleva por nombre “Carrera a 10” y las instrucciones son:
- Para jugar se emplea el siguiente tablero.
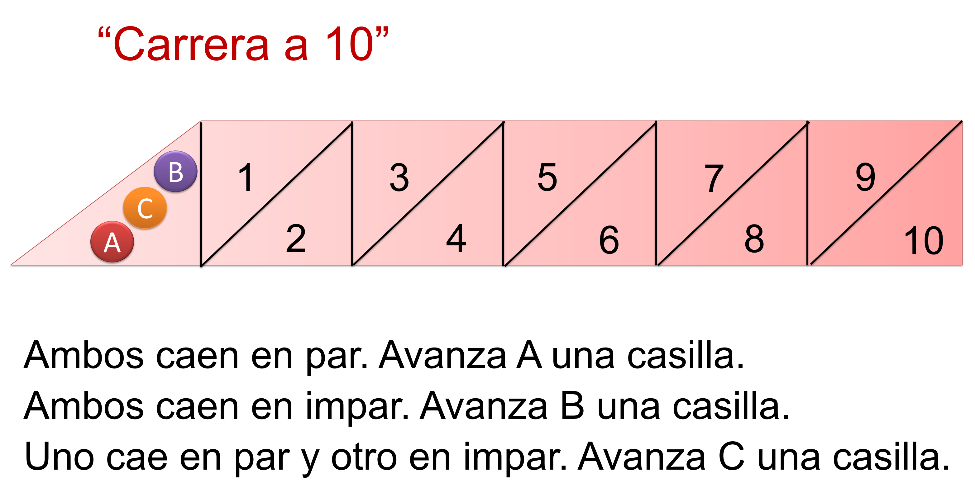
- Los tres jugadores A, B, y C, colocan su ficha en la casilla de salida.
- Uno de los jugadores (no importa quién) lanza los dos dados simultáneamente.
- Después de que avance el jugador al que le haya correspondido hacerlo, se pasan los dados a otro jugador y se repite el procedimiento de la imagen. Gana el que llegue a la casilla 10.
- Se juegan 3 rondas, registrando el resultado durante cada juego.
Con la dinámica del juego explicada, se analizan las siguientes preguntas:

Se plantea la situación para resolver el primer inciso: ¿Alguno de los jugadores tiene alguna ventaja en el juego?
Para responder, se debe calcular las probabilidades que tiene cada jugador de avanzar en el juego.
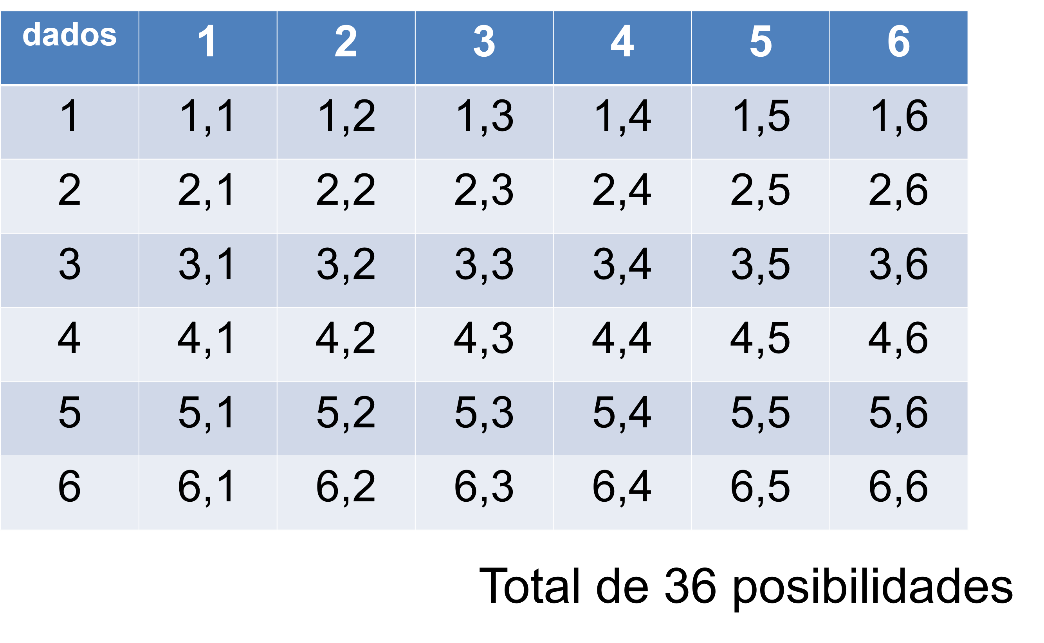
Se emplea una tabla que muestra todos los pares de números que se forman al realizar el experimento de lanzar los dos dados, a partir del cual se pueden calcular las probabilidades de ocurrencia.
Para que el jugador “A” gane, deben caer dos números pares. Entonces: Se le llama “A” a la probabilidad de obtener dos pares.
Parejas de Pares igual a 9
Posibilidades totales igual a 36
P(A) igual a 9 de 36, es decir, 1/4.
Para que el jugador “B” gane, deben caer dos números impares, entonces:
Se llama “B” a la probabilidad de obtener dos números impares.

Parejas de impares igual a 9
posibilidades totales igual a 36
P(B) igual a 9 de 36, es decir, 1/4.
Para que el jugador “C” gane, debe caer un numero par y uno impar. Entonces, se llama “C” a la probabilidad de obtener un par y un impar juntos.
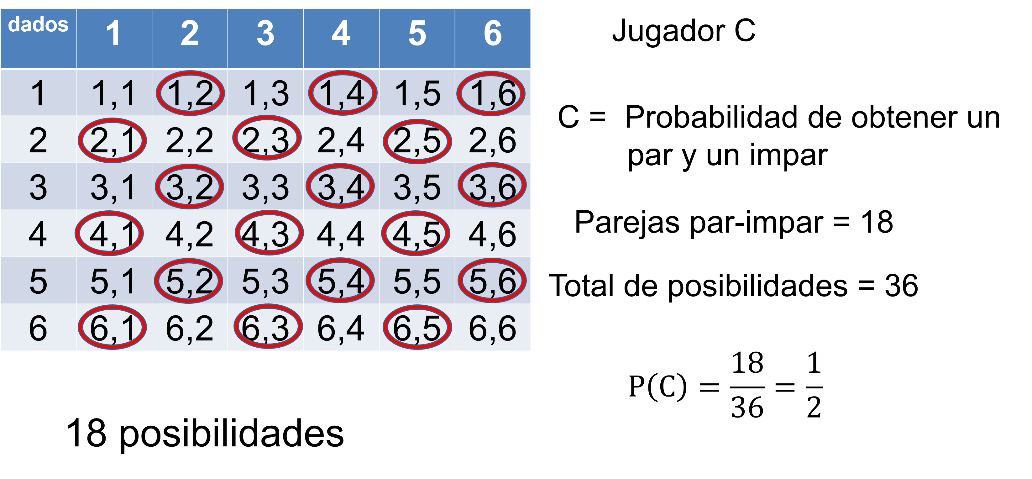
Parejas par-impar igual a 18
posibilidades totales igual a 36
P(C) igual a 18 de 36, es decir,
18/36 que equivale a 1/2.
Aquí se observa que la probabilidad del evento A y del evento B son iguales, por lo que se puede concluir que el jugador “C” tiene ventaja ya que:

Para la segunda pregunta:

En las probabilidades de que cada jugador gane el juego, el que tiene mayor ventaja de ganar es el “C”.
Tercera pregunta. Según las probabilidades de ganar el juego ¿Los resultados son Equiprobables o No equiprobables?
Para responder esta pregunta, se realizó el juego en tres ocasiones para verificar si las probabilidades calculadas se cumplen de forma experimental.
Teniendo los siguientes resultados, se concentraron en una tabla de doble entrada que registra el lugar en el que quedó cada jugador.
Para el primer juego:
El jugador A quedó en segundo lugar.
El jugador B quedó en tercer lugar.
El jugador C en primer lugar.
Para el segundo juego.
El jugador A quedó en tercer lugar.
El jugador B en segundo lugar.
El jugador C en primer lugar.
Para el tercer juego.
El jugador A quedó en segundo lugar.
El jugador B en tercer lugar.
El jugador C en primer lugar.
Lo anterior permite concluir que se cumple la predicción del cálculo de las probabilidades de avanzar y ganar el juego.
Según los resultados, se tiene que el jugador que tiene más probabilidad de ganar el juego es el jugador C, y que los jugadores A y B se alternan el lugar en probabilidad, al tener la misma oportunidad de ganar, aunque esa probabilidad es menor que la del jugador C de ganar.
Por lo tanto, el juego tiene resultados NO EQUIPROBABLES. Es decir, el juego no es justo para todos.
Pero ¿Cómo se puede hacer para que el juego tenga resultados equiprobables?
Para que sea EQUIPROBABLE, se necesita hacer que el juego sea justo para todos con este procedimiento:
Hacer que cada uno de los jugadores, es decir, el jugador A, el jugador B y el jugador C elijan cada uno cualquiera de las siguientes opciones.

Otra opción para que el juego tenga resultados equiprobables es.
Que el juego tenga 6 jugadores con las mismas probabilidades de ganar el juego. Es decir, con cada una de las opciones anteriores, ya que todos tienen 1/12 como probabilidad. Esto también implica el aumento del número de casillas para avanzar, al menos para tres tiradas por personas.
Entonces, si al problema se le ajustan las reglas, se transforma en un juego justo.
En el ejercicio anterior se supo reconocer un juego en el que hay resultados NO EQUIPROBABLES por distintos factores.
De este modo, la forma que se plantea para jugarlo puede reformarse de tal manera que el juego sea justo, no solo para los 3 jugadores, sino también para una mayor cantidad de jugadores. Es decir, plantear nuevas reglas de juego.
Revisa una situación más.
Emilio, Olga, Diana y Jesús, juegan con una ruleta como la siguiente.


Según las condiciones planteadas en el juego, se resuelven las preguntas:

Ante la pregunta: ¿Todos los jugadores tienen las mismas probabilidades de ganar? Se deben calcular las probabilidades de los eventos de cada uno de ellos.
Para Emilio, solo ganará si sale un número par que sea igual o menor que 10.

Con respecto a Olga, ganará si sale un número igual o mayor que 11.
Diana gana si sale un número negro.

En el caso de Jesús, gana si sale un número impar que sea rojo.

Según los resultados obtenidos para cada jugador, todos tienen diferentes probabilidades de ganar, y en el caso específico de Jesús, no tiene ninguna posibilidad de ganar.
Lo anterior obedece a que Emilio tuvo una probabilidad de 25%, Olga y Diana tienen una probabilidad de 50% y Jesús una probabilidad de cero.
La segunda pregunta indica: ¿Quién tiene la mayor probabilidad de ganar?
Son dos los jugadores que tienen mayor probabilidad, y son Olga y Diana, ya que tienen una probabilidad de 50% cada una.
Y para la tercera pregunta, “¿Quién tiene la menor probabilidad de ganar?”, se trata de Jesús, ya que obtuvo una probabilidad de 0%, lo que nos dice que él no tiene ninguna posibilidad de ganar.
Con esto se puede concluir que el juego NO ES JUSTO, debido a la diversidad de los resultados obtenidos, por lo que se dice que esos resultados son “no son equiprobables”.
Para la cuarta pregunta, “¿Cómo se modifican las condiciones del juego para que todos tengan las mismas probabilidades de ganar?”, se tienen varias opciones para hacer que el juego sea justo.
Una de ellas es cambiar las reglas del juego para que todos tengan las mismas posibilidades de ganar.
Otra es cambiar las reglas del juego solo para los dos jugadores que tienen menor probabilidad de ganar, que es lo que aquí se realiza:
Para el caso de Emilio y de Jesús, queda del siguiente modo:
- Para Emilio, que gane si cae un número en rojo.
Así, la probabilidad de ganar para él es:
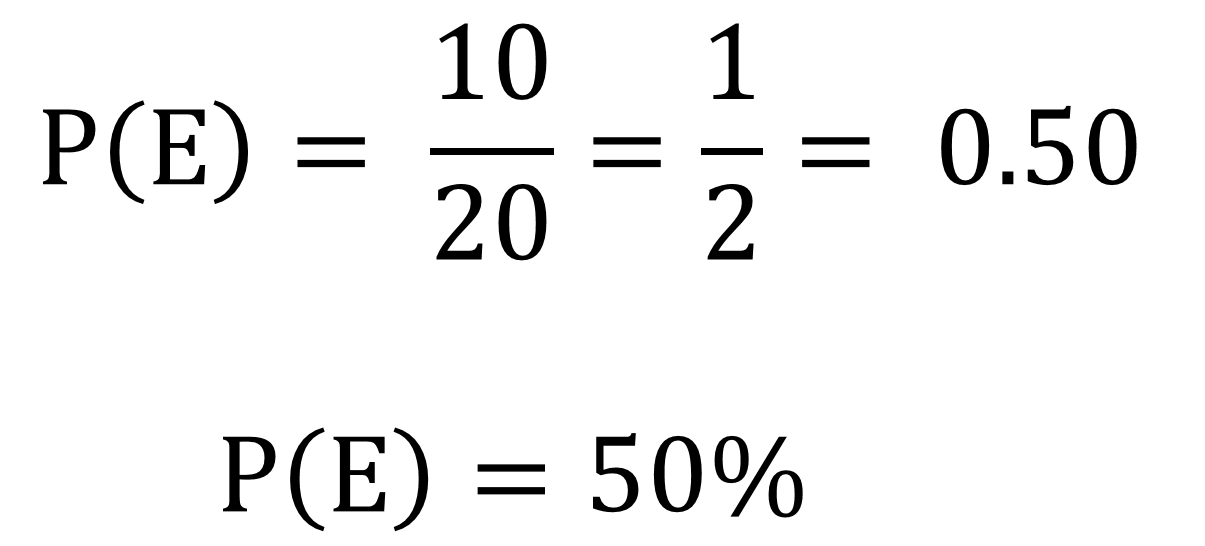
Ahora, para Jesús se necesita que gane si cae un número menor o igual a 10.
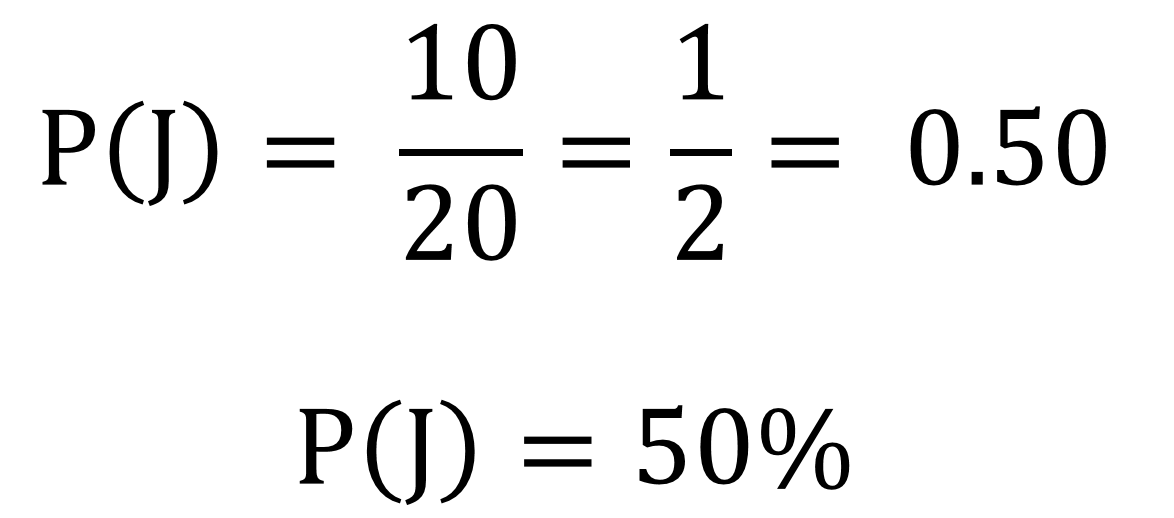
Con estos resultados para Emilio y Jesús, se puede decir que, para los cuatro jugadores, ya existe la misma posibilidad de que gane el juego cualquiera, porque la probabilidad que tiene ahora cada uno de ellos es de 50%.
Por lo tanto, se concluye que ahora sí el juego es justo, ya que los resultados obtenidos para todos son EQUIPROBABLES.
Has aprendido a analizar un juego y determinar cuándo es justo o no para los jugadores. Del mismo modo, aprendiste a modificar las condiciones para que los juegos que no sean justos lo sean.
Para lo anterior, ya sabes que primero se debe determinar si los resultados son equiprobables o no.
El reto de hoy:
Toma un juego de los muchos que existen y jueguen entre varios participantes para analizar si es equiprobable o no.
Si no es equiprobable, determina cómo puedes cambiar las reglas del juego de tal forma que sea justo para todos.
Por ejemplo, la lotería mexicana.

Cada una de las tarjetas cuenta con 9 figuras, y las figuras se repiten en varias de las tarjetas.
¿Alguna vez te has fijado cuáles se repiten más?
Supón que todas las figuras se repiten el mismo número de veces. Cuando no se ocupan todas las tarjetas, algunas se repiten más que otras.
Cuando esto pasa ¿Influye en que tengas mayor o menor probabilidad de ganar?
El juego bajo estas condiciones ¿Es justo? ¿En qué condiciones se puede hacer un juego que no sea justo?
Es un reto para reflexionar y poner en juego lo que has estudiado.
Lee la siguiente apostilla del astrofísico británico Arthur Stanley Eddington: “Es imposible encasillar a la Física moderna en predecir todo con un determinismo perfecto, porque desde su planteamiento ella trata con probabilidades”.
¡Buen trabajo!
Gracias por tu esfuerzo.
*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.







Login to join the discussion