Pensar en reversa
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:57Pensar en reversa
Aprendizaje esperado: determinación de múltiplos y divisores de números naturales. Análisis de regularidades al obtener los múltiplos de dos, tres y cinco.
Énfasis: utiliza estrategias de cálculo mental para obtener múltiplos y divisores de diversas cantidades entre un par de números.
¿Qué vamos a aprender?
Aprenderás a utilizar estrategias de cálculo mental para obtener múltiplos y divisores de diversas cantidades entre un par de números.
¿Qué hacemos?
Antes de iniciar con la sesión de hoy, recuerda algunos conceptos matemáticos que revisaste la semana pasada, por ejemplo: ¿Qué son los múltiplos de un número?
Los múltiplos son todos los números que obtenemos al multiplicar un número natural por todos los números naturales.
Cuando se divide un número natural entre otro y se obtiene como cociente un número entero y el residuo de la división es cero, se dice entonces que, el dividendo es múltiplo del divisor y del cociente.
Actividad 1
Vas a encontrar los múltiplos o divisores de un número natural, pero lo harás en reversa. ¿En reversa?
Sí en reversa, se te presentará un número que es un múltiplo y tu tienes que encontrar de qué números puede ser múltiplo.
Antes tenías dos números y encontrabas sus múltiplos, ahora será al contrario.
Va el primero, ¿De qué números puede ser múltiplo el 56?
Encuentra por lo menos dos números naturales que al multiplicarlos se obtenga 56.
Cuando los hayas encontrado, escríbelos en tu cuaderno.
Puedes intentar con la división. Tendrías que encontrar los divisores de 56.
El 2 y el 28 son divisores del 56, o dicho de otra forma, 56 es múltiplo de 2 y de 28.
¿Crees que la respuesta anterior es correcta?
Hay que comprobarla. Multiplica 2 por 28, lo cual da 56.
2 x 28 = 56
Es correcta, pero ¿Cómo se hizo para encontrarlos?
Tomando en cuenta lo que se ha aprendido en sesiones anteriores, primero reconocer que 56 es un número par, así que todos los números pares se puede dividir entre 2, porque son múltiplos de él.
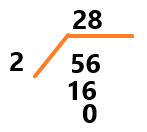
Eso que se hizo fue pensar en reversa. En lugar de multiplicar a ciegas, encontraste dos divisores de 56, sabiendo que es un número par.
¿Puede haber más números que son divisores de 56, o que 56 es múltiplo de ellos?
Es probable que hayas identificado el 14 y 4, o tal vez el 8 y 7
14 y 4
8 y 7
¿Por qué esos números son divisores de 56?
Porque si multiplicas 14 x 4 te dan 56 y también 8 x 7 son 56
8 x 7 = 56
4 x 14 = 56
¿Cómo se puede saber que podían también ser esos números?
Pues una forma sería ir a la tabla de multiplicar de 7 y 8.
Otra, pensar en partir a la mitad el 8, eran 4, pero para conservar el mismo resultado, entonces se tenía que duplicar el 7, eso da 14, luego multiplicar 4 x 14, para ver si resultaba lo mismo y pues sí salió 56.
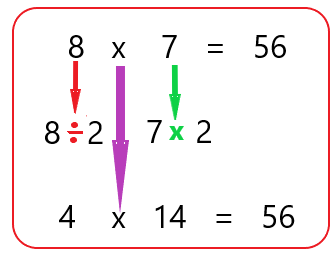
Como puedes observar, las diferentes estrategias que se ponen en juego permiten obtener respuestas. Este ejercicio también muestra que en Matemáticas hay más de una respuesta correcta.
Por eso es importante que simepre que se piense en una respuesta, se compruebe si responde a la pregunta del problema.
Una pregunta más, ¿Estos números serán los únicos divisores de 56?
Si sigues el mismo razonamiento con el 2 x 28, entonces a 2 lo puedes dividir a la mitad, pero entonces tendrías que duplicar el 28.
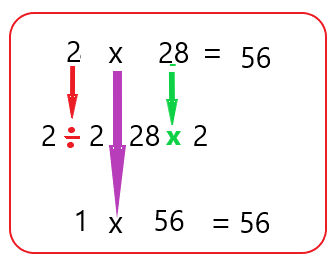
¿Estará bien que 1 x 56, sea 56?
Si porque todos los números multiplicados por 1, dan el mismo resultado, lo que hay que comprobar es que 56 y 1 son divisores de 56, haciendo las divisiones, observa 56 entre 1 es igual a 56 y sobra 0, y 56 entre 56 es igual a 1 y también sobran 0. Ten presente lo siguiente:

Ahora, regresa a los múltiplos y busca los múltiplos del 9 que estén entre 70 y 100.
Los múltiplos de 9 que están entre 70 y 100 son el 72, el 81, el 90 y el 99.
¡Es correcto! porque multiplicar 9 por 8 da como resultado 72, 9 por 9 da 81 y 9 por 10 es 90 y luego si sumas otros 9, obtendrás el 99, que es lo mismo que 9 x 11.
9 x 8 = 72
9 x 9 = 81
9 x 10 = 90
9 x 11 = 99
Los múltiplos de 9
son 72, 81, 90 y 99
¿Cómo se llegó a ese resultado?
Es una estrategia que ya trabajaste en una sesión anterior. Los múltiplos que pidió deben estar entre 70 y 100; así que en vez de estar multiplicando, se dividió 70 entre 9 y no era una división exacta, en cambio, 9 x 7 son 72
63 + 9 = 72, y así se sigue sumando 9 hasta llegar a 90
Lo anterior, es pensar en reversa, porque se buscó el divisor y luego se fue sumando 9
Ahora, resuelve otro desafío. Sabemos que el 4 es múltiplo de 2 y los números 20, 28, 36, 40 son múltiplos del 4, pero ¿Serán o no serán múltiplos del 2?
Los números: 20, 28, 36 y 40 son múltiplos del 4,
Pero, ¿son múltiplos de 2?
Observaste que todos los números naturales que terminan en cifra par o cero son múltiplos del 2.
Los múltiplos de 4 también terminan en cifra par. Entonces ¿Todos sus múltiplos son múltiplos de 2 también?
Entonces todos los números que se pueden dividir entre 4, también se pueden dividir entre dos.
Sí, porque todos los múltiplos de 4 son pares y el 2 divide a todos los números pares.
¿Todos los múltiplos de 2 también son múltiplos de 4?
Ya trabajaste con el 2 y el 4 ahora, analiza otros números. Pon mucha atención, el número 10 es múltiplo de 5, porque 5 x 2 = 10 entonces responde si los múltiplos de 10, serán también múltiplos de 5

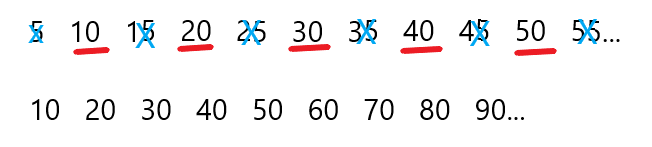
Como puedes observar, se registraron algunos múltiplos de 5 y abajo algunos múltiplos de 10. Lo que se puede encontrar es que todos los múltiplos de 10 están entre los múltiplos de 5 entonces, puedes llegar a la conclusión de que todos los múltiplos de 10 también son múltiplos de 5.
Ahora observa si sucede lo mismo al revés, es decir, si todos los múltiplos de 5 son múltiplos de 10.
Se puede demostrar que los números tachados son múltiplos de 5, pero no están entre los múltiplos de 10, así que se puede decir que no todos los múltiplos de 5 son múltiplos de 10.
Ahora, observa bien ¿5 y 10 son divisores de 80?
5 y 10 sí son divisores de 80, porque al dividir 80 entre 5 toca a 16 y el residuo es 0 luego si dividimos 80 entre 10, toca a 8 y el residuo es 0.

¿Qué otros números serán divisores de 80?
Piensa en la respuesta y anótala en tu cuaderno.
Otro divisor de 80 es el 2 y se puede comprobar haciendo la división de 80 entre 2, lo cual da 40 y sobra cero. La división es exacta.
El 4 también es divisor de 80, porque si divides 80 entre 4, toca a 20 y no hay residuo.
Hay otro más, el uno, porque 80 entre 1 da 80 y el residuo es cero.
Otro divisor de 80 es 80, porque 80 entre 80 toca a 1 y el residuo es 0.
Como pudiste darte cuenta, es muy fácil y divertido aprender a encontrar múltiplos y divisores de un número natural.
El reto de hoy:
Comparte con alguien cercano los ejercicios que hiciste en esta sesión, explícale como obtuviste los resultados y por qué nos números son múltiplos de otros.
Si te es posible, consulta otros libros y materiales para saber más sobre el tema.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/





Login to join the discussion