Operaciones y relaciones
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:24
Operaciones y relaciones
Aprendizaje esperado: concibe las matemáticas como una construcción social en la que se formulan y argumentan hechos y procedimientos matemáticos.
Énfasis: vincular conceptos fundamentales.
¿Qué vamos a aprender?
Los materiales que utilizarás son tu cuaderno de apuntes, bolígrafo, lápiz, goma y colores.
En el momento que consideres necesario, consulta tu libro de texto.
Las Matemáticas son amplias y diversas, con operaciones básicas que ya conoces y emplean desde su educación primaria. Asimismo, cada operación tiene un amplio significado y versatilidad en su aplicación.
Durante la sesión se analizarán características, propiedades y usos de las operaciones básicas conocidas.
¿Qué hacemos?
Comienza con la operación que tal vez, fue la primera que empleaste. Pero ¿Cuál es esa operación?
Desde antes de comenzar tu educación formal, has empleado las operaciones de adición y sustracción, es decir, la suma y la resta.
Estas dos operaciones ya las conoces e incluso, las has utilizado en la solución de diversos problemas.
De este modo, reconocerás desde sus elementos, propiedades y utilidad: Se inicia con los elementos de la adición, en la suma de 3 más 6 más 4, igual a 13. Los números 3, 6 y 4 son los sumandos y el 13 es el resultado o suma.
En el caso de la sustracción, por ejemplo: 73 menos 47 es igual a 26. El número 73 es el minuendo, el número 47 es el sustraendo y el número 26 es la resta o diferencia.
Analiza a continuación otras diferencias entre las dos operaciones:
La sustracción es la operación inversa a la adición; ambas son operaciones complementarias, es decir, cualquier cálculo de resta se puede resolver sumando desde el sustraendo. Por ejemplo:
Se tiene la resta de 10 menos 7, igual a 3; también es posible decir que 10 es igual a 7 más 3.

Incluso se puede afirmar que este proceso es la comprobación de la resta.
Observa así también, las siguientes operaciones:
25 más 30, más 5, es igual a 60
Y que, del mismo modo, se puede calcular:
25, es igual a 60, menos 30, menos 5.
30, es igual a 60, menos 25, menos 5.
5 es igual a 60 menos 25 menos 30.
Al analizar el ejercicio anterior, dos de los sumandos se encuentran restando al resultado o suma, por lo que las igualdades son verdaderas.
Si se tienen dos números restando ¿Cómo se resuelve esta operación? ¿Acaso es la única forma de realizar este ejercicio?
Observa el resultado o suma; a éste se le restan dos números, es decir, los sumandos.

Esto no significa que sean dos restas al mismo tiempo, y para resolverla, se cuenta con dos métodos:
Primero: Restar 60, menos 30, igual a 30 y restarle 5, es igual a 25. Así, solo se tiene un minuendo y un sustraendo para cada caso.
Otra forma de resolverla es sumar los dos números que están restando, es decir: 30 más 5, igual a 35.
Posteriormente, el resultado 35 se resta a 60, es decir, 60 menos 35, es igual a 25.
Como se ha demostrado, los dos procedimientos dan el mismo resultado: En el primero se realizan dos restas y en el segundo, una suma y una resta. Esta fue la comprobación que se realizó para la primera operación.
Comprueba las otras dos operaciones, toma nota en tu cuaderno y reafirma lo trabajado hasta el momento, reflexionando lo siguiente:
¿Ocurre de igual modo con las fracciones?
Para responderlo, se tiene el siguiente ejercicio: Los maestros de Artes y Matemáticas de una escuela van a montar una exposición denominada “La numeración de las artes”. En ella se muestran cuadros mágicos con diferentes series de números.
Completa el cuadrado mágico con la siguiente serie de fracciones: Dos tercios, tres tercios, cuatro tercios, cinco tercios, seis tercios, siete tercios, ocho tercios, nueve tercios y diez tercios.
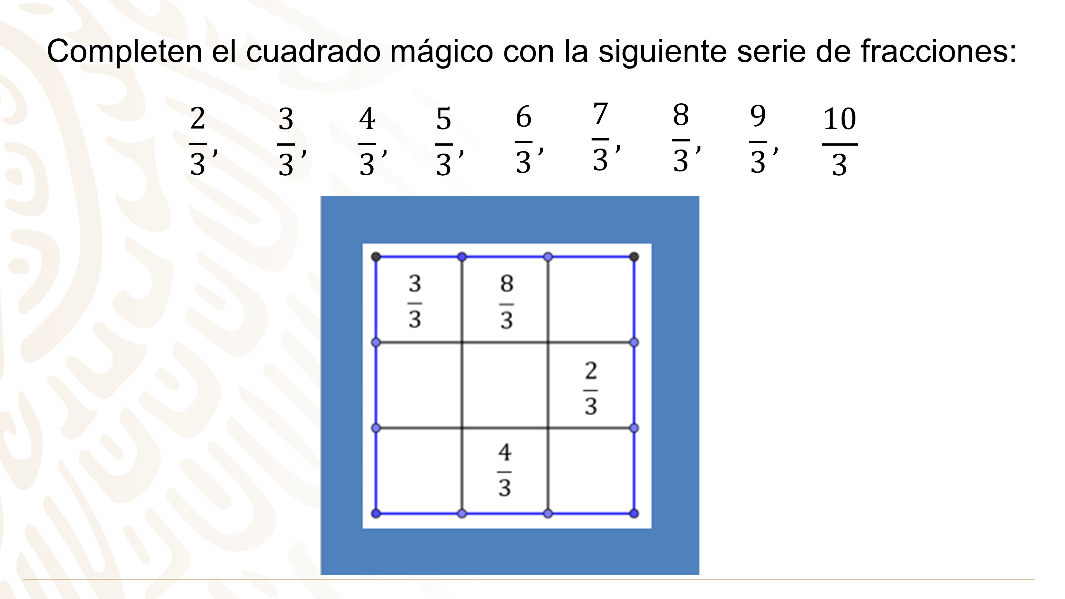
En el cuadro mágico están ubicadas sólo cuatro fracciones y se desean llenar las casillas faltantes con las fracciones indicadas en la serie.
Ya saben que, en el cuadro mágico con fracciones, todas las horizontales, verticales y diagonales suman el mismo valor.
¿Cuál es el valor que debe de sumar el cuadro mágico?
Aunque ese dato no lo proporcionan en el ejercicio, es posible calcularlo porque es una serie numérica de fracciones ordenadas. Es así como el dato central se va a utilizar.
De la serie ordenada se ubica el dato central; al ser nueve datos, el quinto es el central: Seis tercios.

Éste se multiplica por tres porque se sabe que es un cuadrado mágico de tres casillas por tres.
Se obtienen seis tercios por tres enteros, igual a 18 tercios, igual a seis enteros.
Si seis tercios es igual a dos enteros, al multiplicarlo por tres es igual a 6.
En consecuencia, el cuadrado mágico debe de sumar 18 tercios o seis enteros.
Una vez conocido el valor de la suma, es posible llenar las casillas con los números de la serie proporcionada utilizando las operaciones de adición y sustracción.
Inicia con el renglón en donde se conocen las fracciones de dos casillas.
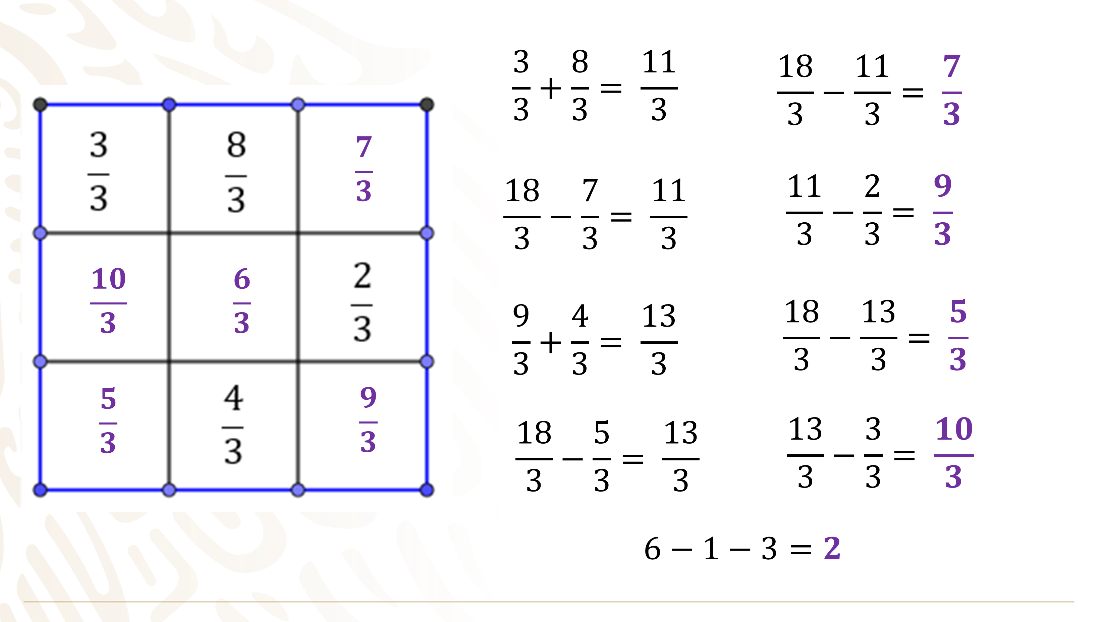
Suma tres tercios más ocho tercios; al tener el mismo denominador se suman los numeradores y el resultado es once tercios.
Se restan once tercios a dieciocho tercios; se obtienen siete tercios y se coloca en la esquina superior derecha.
Por otra parte, en la columna donde se colocó la fracción siete tercios, ya se conocen dos fracciones.
Para encontrar la tercera fracción, se realiza una resta: Dieciocho tercios, menos siete tercios, es igual a once tercios.
A este resultado se resta la otra fracción conocida: Once tercios, menos dos tercios, es igual a nueve tercios; esta fracción se coloca en la tercera casilla de la columna.
La fracción nueve tercios se suma a cuatro tercios, igual a trece tercios. Ésta se resta a dieciocho tercios, igual a cinco tercios, y se registra en la 1° casilla de esa fila.
En esta columna solo se desconoce el valor de la casilla de en medio. Por lo tanto, se resta a dieciocho tercios, menos cinco tercios, igual a trece tercios.
Después se restan trece tercios, menos tres tercios, igual a diez tercios, y la fracción se escribe en la casilla central de la columna.
Solo falta encontrar el valor de la casilla central del cuadrado mágico. Pero ¿qué se hace para completarlo?
Una opción es considerar los números enteros de la diagonal para realizar la operación, es decir: Tres tercios es igual a un entero; nueve tercios es igual a tres enteros.
Realiza mentalmente el cálculo de las operaciones: Seis menos uno, menos tres, es igual a dos. Por lo tanto, la fracción de la casilla central es seis tercios o dos enteros.
Ya completaste el cuadrado mágico. Para encontrar el valor de la última casilla, se pudo encontrar cuál fracción de la serie faltaba por colocar: Seis tercios.
Ya sabes que las operaciones básicas como la adición y la sustracción permiten resolver una gran variedad de retos.
Siguiente caso:

Antes de aplicar una estrategia de solución se deben reconocer los datos proporcionados y los requeridos. Pero ¿cuáles son los términos de una sustracción?
Considera a:

El ejercicio menciona la suma de los términos: “m” más “s”, más “d”, igual a 700; se tiene la primera ecuación.
Para la segunda ecuación toma en cuenta la segunda parte del ejercicio: El sustraendo “s” es igual a la quinta parte del minuendo “m”.
Y por ser de tres incógnitas, falta la tercera ecuación. Ésta se puede plantear por medio de la propiedad de la sustracción, cuyo minuendo es igual a la suma del sustraendo, y la diferencia “m” es igual a “s” más “d”.
De este modo, ya se tiene el planteamiento de las ecuaciones con los términos de una sustracción.
Se sustituye la ecuación 3 en la ecuación 1, es decir: “m” es igual a “s” más “d”; así “m” más “m” es igual a 700.

Al simplificar se tiene “2m” es igual a 700; se dividen ambos miembros entre 2 y “m” es igual a 350.
Con este valor, se calcula el valor de “s” sustituyendo en la ecuación 2; “s” es igual a 350 entre 5, igual a 70.
El valor solicitado del sustraendo es 70.
Ahora, para comprobar los resultados, se emplea la primera ecuación.
El minuendo es igual a 350 y el sustraendo es igual a 70.
La diferencia de “m” y “s” es la resta de 350, menos 70, cuyo resultado es “d” igual a 280.

Al sumar los tres términos de la sustracción: 350 más 70, más 280, es igual a 700, siendo correcta y verdadera la primera ecuación. De igual modo, puedes comprobar las otras dos ecuaciones.
Has resuelto ejercicios con dos operaciones: La adición y la sustracción con diferente grado de complejidad. Sin embargo, estas no son las únicas operaciones conocidas.
Se analiza el siguiente ejercicio que involucra la unión o separación de grupos iguales, es decir, aplicar la multiplicación y la división.

El ejercicio menciona fracciones y dos grupos con diferentes condiciones, además de que están combinadas las condiciones.
Se deben identificar, por tanto, los datos del ejercicio para encontrar la mejor estrategia de solución.

Del total, la fracción de quienes tocan algún instrumento es un cuarto.
Es importante resaltar que son dos tipos de preguntas. Por esta razón, se comienza con el cálculo de la primera.
Para determinar cuántos alumnos hombres tocan un instrumento, se calcula en total cuántos tocan un instrumento.
Estos son la cuarta parte del total de alumnos, por lo que se multiplica un cuarto por 180; se convierte 180 a fracción al colocar un “uno” como denominador.

Al realizar el producto directo, 1 por 180, es 180; 4 por 1, es 4, se divide 180 entre 4 y se obtiene 45.
Son 45 alumnos en total quienes tocan algún instrumento.
Ahora, de los 45 alumnos se deben calcular cuántas son alumnas.
Si ellas son tres quintas partes, se multiplican tres quintos por 45, que se expresa como fracción.
Al realizar el producto directo, 3 por 45 es 135, y 5 por 1, es 5; se divide 135 entre 5 igual a 27.
Entonces, 27 alumnas tocan algún instrumento.
Pero con este cálculo aún no se contesta la pregunta del ejercicio porque se requiere el número de hombres que tocan algún instrumento.
Al total de alumnas y alumnos quienes tocan algún instrumento se le resta el número de mujeres con la misma condición, es decir, 45 menos 27 es igual a 18.
Son 18 alumnos hombres los que tocan algún instrumento.

Para la segunda pregunta del ejercicio, se solicita la fracción de alumnas quienes tocan algún instrumento del total de alumnos del grado.
Se comienza sustituyendo en ese mismo orden, es decir, se dividen 27 alumnas —quienes tocan algún instrumento—, entre 180 que es el total de alumnas y alumnos de tercer grado que conforman el coro de la escuela.
Se simplifica la fracción, dividiendo numerador y denominador entre 9, igual a tres veinteavos.
En el ejercicio anterior se realizaron sustracciones, multiplicaciones y divisiones con números enteros y fracciones. Esto denota la versatilidad del uso de las operaciones básicas.
Además, se utilizaron sus propiedades al simplificar expresiones numéricas o algebraicas que facilitan la solución de los ejercicios.
Asimismo, es importante mencionar que estas propiedades no se aplican a todas las operaciones.
Pero ¿De cuáles propiedades se hablan?
-La propiedad del elemento neutro
-Las propiedades asociativas, conmutativas, distributiva
-Y las leyes de cancelación.
La aplicación de estas propiedades está presentes al despejar la variable en la ecuación.
Además, en la cancelación del número 2 —que multiplica y divide por ser operaciones inversas—, y por encontrarse en el mismo lado de la igualdad.
Como se sabe, las propiedades cambian de una operación a otra, sin embargo, otras no se pueden aplicar a ciertas operaciones.
En el caso del elemento neutro para la suma y resta, se utiliza el cero porque todo número sumando o restado con el cero da el mismo número.
Pero en la multiplicación y la división, el elemento neutro es el número 1, porque no altera la operación y no causa indefinición.
La razón se aplicó al convertir los números enteros a fracciones, colocando el 1 en el denominador para después realizar el producto directo.
Tras esto, se sigue con el análisis de otras propiedades por medio de un nuevo caso:

Tras resolver el ejercicio, a través de la solución se resaltan las propiedades y cómo éstas facilitan el proceso.
El depósito contenía 350 litros de agua y se agrega el flujo de agua de las llaves.
Para ello, se expresa la razón entre los litros y el tiempo en minutos, y se considera como igual la velocidad del agua ingresada o saliente en un minuto.

Para la llave 1, la razón es 120 litros en 8 minutos, es decir, 15 litros por minuto.
Para la llave 2, al verter el líquido, su razón es negativa: Menos 42 litros en 7 minutos, o bien, menos 6 litros por minuto.
Y para la llave 3, es 144 litros en 9 minutos, es decir, 16 litros por minuto.
Se debe calcular entonces, la velocidad por minuto con la cual entra o sale el agua. Es posible calcular cuánta agua ingresa y se vierte en los 50 minutos, indicados en el ejercicio por las 3 llaves.
Para ello, se multiplica: 15 por 50, más 6 negativo por 50, más 16 por 50.
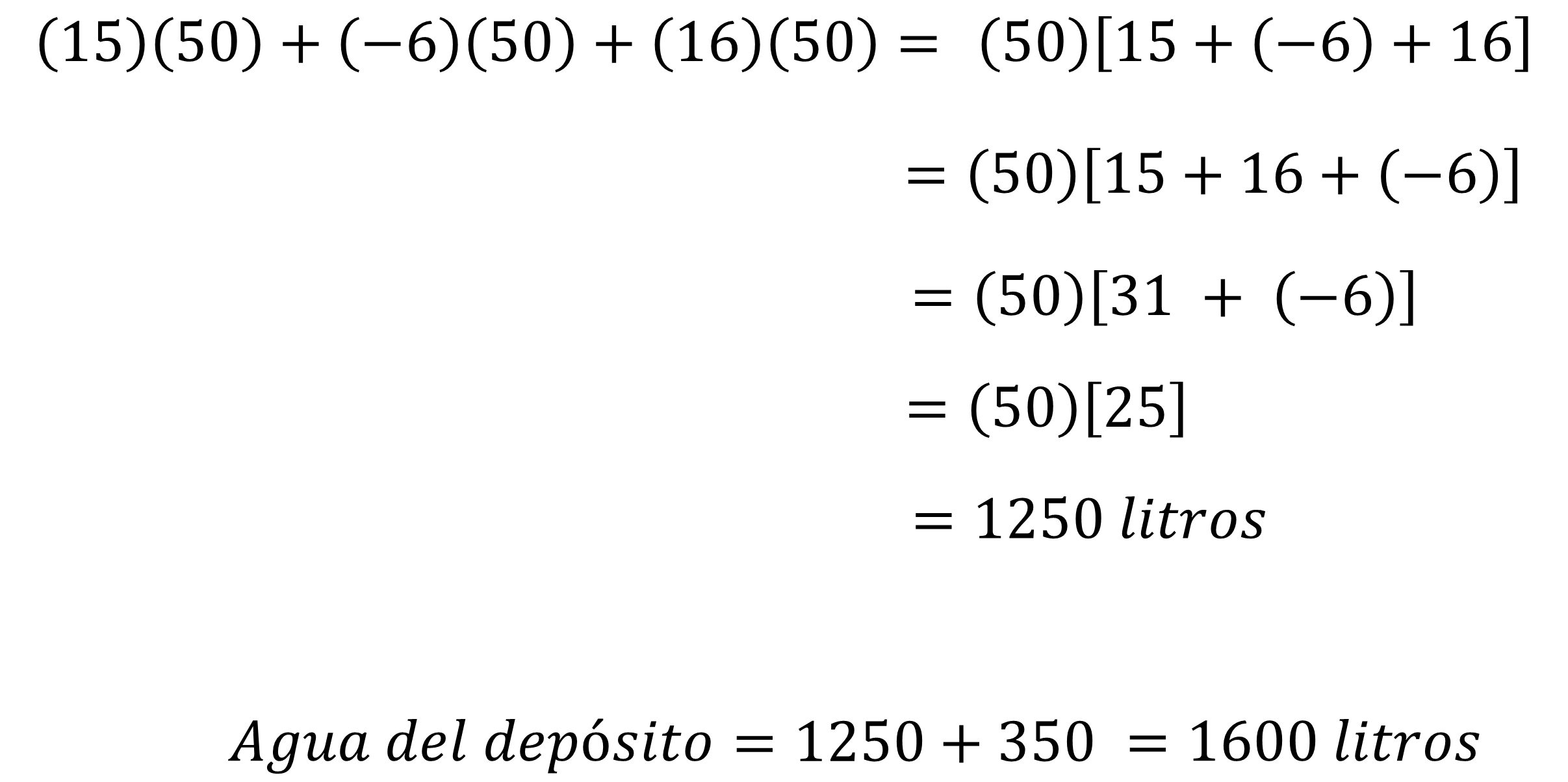
Observa que, en cada sumando, el término 50 es un factor común, por lo cual se puede factorizar.
Se anota el factor común 50, y se abre paréntesis para anotar la suma de cada uno de los tres factores: 15 más 6 negativo, más 16 y se cierra el paréntesis.
Por jerarquía de operaciones se realiza primero la operación indicada en el paréntesis:
15, más 6 negativo, más 16; para agilizar el proceso se suman primero los números positivos y después, el número negativo: 15, más 16, es igual a 31, más 6 negativo, que por ser signos contrarios se restan y su resultado es 25.
Ahora se multiplica 50 por 25, igual a 1 250.
Por último, se suman 1250, más 350 litros de agua que ya están contenidos en el depósito, igual a 1,600 litros.
Analiza algunas partes del procedimiento:
Primero: La razón de la llave 2 al ser desagüe es negativa, y las otras dos llaves al llenar el depósito se consideran con razones positivas.
El factor común identificado permite aplicar la propiedad distributiva de la multiplicación sobre la suma, la cual indica que: El producto de una suma o diferencia es igual a la suma o diferencia de los productos. Esto facilita obtener un solo producto y compactar el procedimiento.
Por último, al momento de efectuar la operación dentro del paréntesis, se aplica la propiedad conmutativa al poner los números positivos, y después el número negativo para facilitar su ejecución.
La práctica te permite desarrollar estrategias de resolución variadas, pero siempre con fundamentos Matemáticos que te faciliten los procedimientos.
Por esta razón, analiza el siguiente ejercicio, donde las potencias de 10 son puntos de referencia importantes del sistema de numeración.
Para facilitar las operaciones, piensen en los números en relación con las potencias de 10.

Analiza el ejercicio, del que se requiere convertir el diámetro de años luz a millas. Ya conoces la equivalencia de un año luz en millas y por lo tanto, se deben de multiplicar los datos proporcionados.
Pero ¿Cuál es la dificultad en este ejercicio?
Que los datos son cantidades muy grandes, incluso en una calculadora sencilla no es posible realizarla. Pero a través del uso de potencias de “base 10” se pueden expresar de una forma sencilla para operar.
Primero, se expresan los datos en notación científica, es decir, con potencias de “base 10”:
Para ello, se considera la parte entera de la cantidad y se cuentan los lugares que se recorre el punto decimal para expresarlo como exponente de la potencia de “base 10”.

Para convertir el diámetro, se multiplica 5.88 por 10 a la doceava potencia por 2 por 10 a la quinta potencia; al realizar el producto de los coeficientes, 5.88 por 2 es igual a 11.76
Las potencias de base 10, al estar multiplicando, se suman los exponentes 12 más 5, igual a 17.
El resultado es 11.76 por 10 a la diecisieteava potencia, pero en notación científica, el coeficiente debe ser mayor o igual a uno y mejor que diez —es decir la parte entera de este—. De este modo, se recorre un lugar el punto decimal y se tiene que el diámetro de la Vía Láctea es de 1.176 por 10 a la dieciochoava potencia millas.
La solución del ejercicio fue ágil gracias al uso de las potencias de base 10.
Durante la sesión se analizaron las operaciones básicas, sus elementos, la relación entre ellas, así como las propiedades y las leyes que facilitan los procedimientos numéricos y algebraicos.
Como ya lo has corroborado, el uso de las potencias de base 10 abrevian las operaciones.
El reto de hoy:
Continúa practicando con ejercicios los conocimientos adquiridos.
Y como decía el matemático y filósofo alemán Gottlob Frege: “Comparo a la Aritmética con un árbol que se desarrolla hacia arriba en una multitud de técnicas y teoremas mientras que la raíz se adentra en las profundidades”, continúa explorando y adentrándote en el mundo de las Matemáticas.
¡Buen trabajo!
Gracias por tu esfuerzo.
*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa*.





Login to join the discussion