Operaciones combinadas con fracciones y decimales

Operaciones combinadas con fracciones y decimales

Aprendizaje esperado: determina y usa la jerarquía de operaciones y los paréntesis en operaciones con números naturales, enteros y decimales (para multiplicación y división, solo números positivos).

Énfasis: usar la jerarquía de las operaciones en la resolución de operaciones combinadas.

¿Qué vamos a aprender?

¿Sabías que Juan de Luna fue el primero que empleó la palabra fractio para traducir la palabra árabe al-Kasr que significa quebrar, romper? De ahí, que las fracciones se conozcan con el nombre de quebrados.

En esta sesión analizarás operaciones combinadas y su correcta resolución en diferentes contextos.

Ten a la mano los materiales para poder seguir la sesión. Cuaderno de la asignatura de matemáticas, en su defecto, hojas de reúso para hacer tus apuntes. Lápiz y goma.

¿Qué hacemos?

Observa la siguiente situación:

“Graciela fue al mercado para hacer las compras para la comida y anotó lo que iba a comprar en una hoja para no olvidar nada. 1.5 kilogramos de pierna de pollo, 0.200 kilogramos de jamón y 0.750 kilogramos de jitomate.”

Graciela preguntó los precios de cada uno de los productos para hacer cuentas y saber cuánto dinero gastaría. Los precios son los siguientes:

La pierna de pollo tiene un costo promedio de 46 pesos el kilogramo.

El jamón cuesta 160 pesos el kilogramo.

El jitomate 24 pesos el kilogramo.”

Con los precios y la cantidad de kilogramos comprados de cada producto, Graciela ya puede establecer la cantidad que debe pagar.

Observa la operación que escribió para encontrar los costos. ¿Ya sabes cuánto tiene que pagar por cada producto? ¿Cuánto tiene que pagar en total?

Primero, ordena la información en una tabla de datos y, posteriormente, escribe las operaciones que permiten obtener el resultado: la pierna de pollo, 46 por 1.5, más el jamón que es 160 por 0.200 y por último sumamos el jitomate 24 por 0.750.

¿Qué pasos se tienes que seguir para resolver las operaciones que se muestran?

Al momento en que Graciela realizó la operación en su casa, resultó una cantidad que no coincidía con el dinero que le habían cobrado. Observa la secuencia de operaciones que realizó Graciela.

Al operar con números decimales puedes omitir los ceros a la derecha y los resultados no cambian, ya que 0.200 es igual a 0.2

Analiza su procedimiento:

Graciela resolvió primero la multiplicación de 46 por 1.5 cuyo producto es 69, procedió a adicionarlo con 160 y su suma resultó 229, lo que multiplicó por 0.2 obteniendo un producto de 45.8, este producto lo adicionó con 24 obteniendo 69.8 y por último multiplico 69.8 por 0.75 y obtuvo como producto final 52.35

Los resultados de cada operación que realizó son correctos, pero si la pierna de pollo cuesta 46 pesos y compró un kilogramo y medio no es posible que el precio de todo sea tan solo 52.35 pesos.

Analiza y encuentra el error que hay en el procedimiento que Graciela realizó.

¿Qué te parece si obtenemos primero el costo por separado de cada producto y al final sumas las cantidades?

Observa la imagen y sigue el procedimiento.

Primero obtén el costo de la pierna de pollo que sería 46 por 1.5 obteniendo un producto de 69 pesos; procede a multiplicar 160 por 0.2 que corresponde a lo que pagó por el jamón, su producto es 32 pesos; después el jitomate, multiplico 24 por 0.75 cuyo resultado es 18; finalmente, adiciona los resultados obtenidos: 69 más 32 más 18 que es igual a 119 pesos.

Por el pollo pagó 69 pesos, le sumas 32 pesos del jamón y 18 pesos del jitomate obtienes 119 pesos que fue la cantidad que pagó por lo que compró, si en los dos casos las operaciones están resueltas correctamente, ¿qué ocasionó no llegar al mismo resultado en ambos casos?

Graciela cometió un error al hacer las operaciones de manera consecutiva de izquierda a derecha, sin seguir un orden jerárquico, al hacer operaciones siempre tienes que respetar un orden específico.

Es común pensar que la resolución de operaciones será siempre de izquierda a derecha, debido a que tu lectura es en ese sentido, pero para poder hacer operaciones correctamente hay que visualizar a las matemáticas como un lenguaje, que tiene reglas y hay que respetarlas para interpretarlo correctamente.

Observa la siguiente operación:

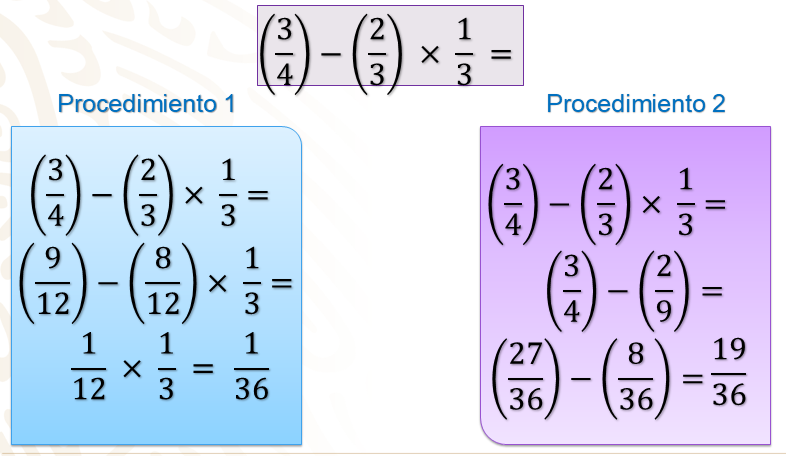
3/4 menos 2/3 por 1/3

Para resolverla, se siguieron dos diferentes procedimientos:

Del lado izquierdo se sigue el siguiente procedimiento:

1. Primero: se obtiene la diferencia entre 3/4 y 2/3, para hacerlo obtienes las fracciones equivalentes 9/12 y 8/12, al tener las fracciones equivalentes ya puedes realizar la sustracción con denominadores en común, obtenemos la fracción 1/12
   Posteriormente: se multiplica el resultado de la sustracción, 1/12 por 1/3, se multiplica numerador por numerador y denominador por denominador obteniendo como producto 1/36
   Ahora, del lado derecho se observa el procedimiento:
2. Primero: se obtiene el producto de 2/3 por 1/3 que es igual a 2/9

Después: haces la sustracción de 3/4 menos el producto anterior, 2/9. Para poder realizar la operación, debes convertir a las fracciones en fracciones equivalentes con igual denominador: 3/4 es igual a 27/36 y 2/9 es igual a 8/36, al resolver la sustracción 27/36 menos 8/36 la diferencia es 19/36

¿Cuál procedimiento es el que tiene la respuesta correcta?

Hay que tener en cuenta que la resta es la operación inversa de la suma, y como en el ejemplo anterior, antes de realizar la suma debiste multiplicar, aquí también deberías de multiplicar antes de hacer la resta.

Al resolver operaciones combinadas, se estableció un orden en su resolución, a esta organización se le conoce como, “Jerarquía de operaciones” y el orden a seguir es el siguiente.

En primer lugar, se realizan las potencias y las raíces, aunque en los casos que estarás trabajando, no vas a considerar todavía este tipo de operaciones.

En segundo lugar, se resuelven las multiplicaciones y las divisiones y, por último, en tercer lugar, las adiciones y las sustracciones.

Cuando las operaciones tienen la misma jerarquía se resuelven de izquierda a derecha.

Ahora observa que Graciela no obtuvo el resultado acertado, porque no siguió la jerarquía de las operaciones, entonces de acuerdo con lo anterior, en el problema de las fracciones, si sigues correctamente la jerarquía de operaciones, el procedimiento correcto es el número 2

En el procedimiento de la izquierda lo primero que se hace es resolver la sustracción obteniendo un doceavo. Al tener una multiplicación, implicada en la operación, significa que debiste resolverla antes de la sustracción.

Y en el procedimiento de la derecha, comenzaste resolviendo la multiplicación y al final realizaste la sustracción, siguiendo adecuadamente la jerarquía de operaciones.

Para estos casos tienes que usar los signos de agrupación: los paréntesis, los corchetes y las llaves, los cuales te permiten modificar el orden de solución de una operación combinada.

Observa una situación que puede ser resuelta utilizando los signos de agrupación.

“Gabriel y Román son joyeros y necesitan fundir 6 piezas de 9.5 gramos de bronce con 20 y media piezas de 20 gramos de plata para hacer una pieza de artesanía.

Al momento de verificar el metal que tenía disponible, Gabriel podía hacer 2 piezas y un tercio de otra, mientras que Román podía elaborar 4 piezas y un cuarto de otra

¿Cuánto metal tienen disponible para sus piezas entre ambos?”

¿Qué procedimiento es el correcto para conocer la masa del metal que tienen disponible para sus artesanías?

Podrías obtener la masa de cada artesanía y posteriormente multiplicarlo por la cantidad de artesanías que pueden hacer.

Primero, para cada artesanía se necesitan seis piezas de bronce de 9.5 gramos, cada una y 20 piezas y media de 20 gramos de plata. Para obtener la masa total de cada pieza suma estos dos conjuntos de datos.

De las artesanías que pueden hacer con el metal disponible, Gabriel tendrá 2 piezas y un tercio de otra, Román 4 piezas y un cuarto; en este caso, habría que sumar para tener el total de piezas y después multiplicarlo para tener la masa total del metal disponible para todas las artesanías.

Podrías hacerlo por separado o podrías expresar en una sola operación todo este proceso, considera que las matemáticas son como un lenguaje y, utilizando los signos correctos, así como el orden adecuado, puedes expresar cualquier operación que desees.

¿Cómo podrías representar en una sola operación todo esto?

Antes de la multiplicación, tienes que resolver la suma del total de artesanías y, por otra parte, la masa de cada una, para que al final se multipliquen entre sí.

Existe una manera y para ello, se utilizan los signos de agrupación como el paréntesis, los corchetes y las llaves.

Agrupa con un paréntesis las operaciones que debes realizar primero.

Pon un paréntesis para delimitar la suma de las artesanías y otro que delimite las operaciones para obtener la masa de cada artesanía, tal como lo muestra la imagen.

A esta secuencia se le conoce como “operaciones combinadas” y hay que tener en cuenta que los signos de agrupación engloban operaciones que se deben resolverse primero.

Es decir que los signos de agrupación se resuelven de adentro hacia afuera.

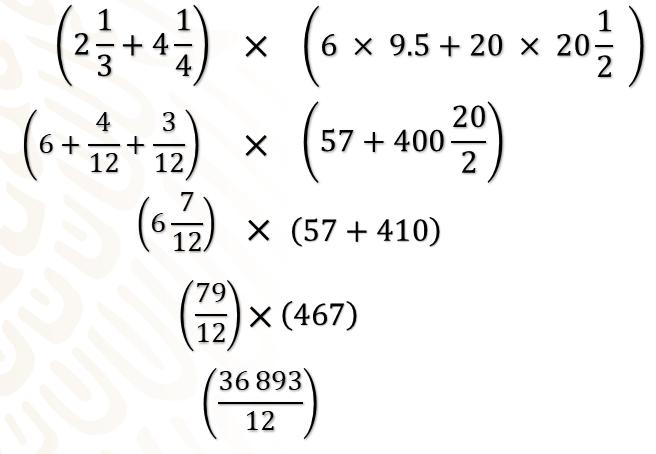
Primero resuelve las operaciones dentro del primer paréntesis: tienes varias sumas, para realizarlas correctamente, sumas los enteros 2 más 4 son seis y la fracción 1/3 y 1/4 los conviertes a fracciones equivalentes con denominador 12; así obtienes la suma 6 más 4/12 más 3/12. En el otro paréntesis: primero resuelves las multiplicaciones: seis por 9.5 es 57, más el producto de 20 por 20 enteros 1/2, que resultaría 400 enteros 20/20

Para continuar, haces la suma de los 6 enteros, más 4/12, más 2/12 obteniendo 6 enteros 7/12. En el otro paréntesis la fracción 400 enteros 20/2 puede reducirse a 410 enteros y obtienes la suma 57 más 410

Para resolver la multiplicación final, convierte 6 enteros 7/12 en fracción impropia, es decir, en 79/12, posteriormente, en el otro paréntesis heces la suma 57 más 410, obteniendo como resultado 467. Finalmente, multiplicas 79/12 por 467 y obtienes 36893/12

El resultado que obtuviste fue de 36893/12, de gramo de cobre y plata para las artesanías.

También pudiste haber encontrado el resultado escrito en forma de número mixto que en este caso sería 3074 y 5/12

Entonces puedes formular la respuesta a este reto, ¿Cuánto metal tienen disponible para sus piezas entre Gabriel y Román?

La respuesta es 3 mil 74 gramos y cinco doceavos.

A continuación, anota la siguiente operación.

El reto será elegir cuál de las opciones de respuesta es la correcta. En el inciso “a”: 12/35 y en el inciso “b”, 15/28

La jerarquía de operaciones determina que estas operaciones tienen el mismo nivel de prioridad

Si realizas la operación de izquierda a derecha, no obtendrías el mismo resultado que si lo haces de derecha a izquierda.

Entonces, cuando se trate de realizar operaciones de este estilo ¿cómo sabrás cuál realizar primero?

Cuando te encuentres este tipo de operaciones con división y multiplicación, siempre se resolverán de izquierda a derecha, y esto se debe a la propiedad conmutativa.

La propiedad conmutativa de la multiplicación dice que el orden de los factores no altera el producto y esto sucede de igual forma en la operación de adición.

Claro, es lo mismo multiplicar 3 por 5 que 5 por 3 o también si sumo 4 más 5 es igual a sumar 5 más 4

Pero la división, así como la sustracción, no son conmutativas, por lo que no podrás variar su orden, y siempre las resolverás de izquierda a derecha, como está escrita en la operación.

Entonces, cuando tienes operaciones del mismo nivel, por ejemplo, multiplicaciones y divisiones, las realizarás siempre de izquierda a derecha.

Siguiendo esta propiedad, debes dividir primero las fracciones, 1/7 entre 1/3; para ello, multiplicas 1/7 por 3, que es el inverso multiplicativo de 1/3; obteniendo el cociente 3/7, y este resultado lo multiplicas por 4/5 obteniendo el producto 12/35, y corresponde al inciso “a”.

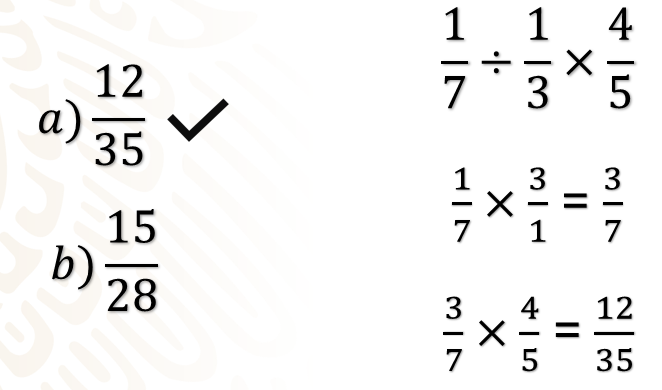
El reto de hoy:

Elabora un organizador gráfico en el que detalles los conceptos e ideas principales, agrega alguna anotación importante, compártela con tu profesora o profesor titular y consulta tu libro de texto en la sección de “Operaciones Combinadas” o “Jerarquía de operaciones”, seguro que encontrarás ejercicios muy interesantes.

El tema es “operaciones combinadas”, y sabes que son expresiones aritméticas que tienen varias operaciones.

Para resolverlas, tendrás en cuenta: primero la jerarquía de operaciones que indica el orden a resolver, primero las potencias y raíces, en segundo lugar, las multiplicaciones y divisiones y al último las sumas y restas. Hay que tomar en cuenta los signos de agrupación: los paréntesis, los corchetes y las llaves y siempre se resuelven las operaciones de adentro hacia afuera.

Por último, considera que, si las operaciones se encuentran en el mismo nivel que marca la jerarquía de operaciones, se resolverán de izquierda a derecha

¡Buen trabajo!

Gracias por tu esfuerzo. 

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html