Oca numérica

Aprendizaje esperado: resolución de problemas que impliquen una división de números naturales con cociente decimal.

Énfasis: analizar los pasos que se siguen al utilizar el algoritmo usual de la división.

¿Qué vamos a aprender?

Analizarás los pasos que se siguen al utilizar el algoritmo usual de la división.

El día de hoy vamos a analizar los pasos que se siguen al utilizar el algoritmo usual de la división y a resolver divisiones hasta obtener como residuo cero.

Necesitas tener a la mano tu cuaderno y tu lápiz, para que vayas resolviendo las divisiones.

¿Qué hacemos?

La primera división que vamos a resolver es: 25 entre 1832

Para empezar, divides 183 entre 25, el cociente es 7 y sobran 8, agregamos el 2, ahora dividimos 82 entre 25 el cociente es 3, sobran 7 enteros, para poder seguir dividiendo lo convertimos a decimal y tenemos que agregar el punto al cociente, entonces es 70 entre 25, el cociente es 2, sobran 20 décimos para poder dividir lo convertimos a centésimos y son 200 entre 25 el cociente es 8 y el residuo es cero y el cociente es 73.28

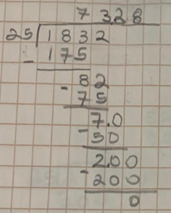
Recuerda que el número que está adentro es el dividendo, el que está afuera divisor, el resultado es el cociente y la cantidad que sobra es el residuo.

Ahora te voy a explicar paso a paso, como obtuvimos el residuo de 0 al dividir 1832 entre 25, primero tomamos la unidad de millar y la centena del dividendo; comparamos que sea igual o mayor al dividendo, en este caso, 18 no es mayor a 25, consideramos ahora la decena, es decir 183 y sí es mayor a 25 buscamos un número que multiplicado por 25 se aproxime a 183 y es el 7, multiplicamos 25 por 7 igual a 175 y lo restamos a 183, sobran 8 y bajamos el 2 de las unidades, para dividir 82 entre 7.

Ahora buscamos un número multiplicado por 25 que se aproxime a 82, sería 3, multiplicamos 3 por 25 es 75 y lo restamos a 82, sobran 7.

Como ya no tenemos números en el dividendo y nuestro residuo no es cero, convertimos los 7 enteros a decimal y agregamos el punto decimal en el cociente. Entonces: 7 enteros son lo mismo que 70 décimos, que los vamos a dividir entre 25.

Buscamos un número multiplicado por 25 que se aproxime a 70 y es el 2, multiplicamos 25 por 2, da 50, le restamos eso a 70 y sobran 20 décimos.

Para dividir los 20 décimos, los convertimos a centésimos, son 200 y, luego, lo dividimos entre 25.

Buscamos un número multiplicado por 25 que se aproxime a 200 y es el 8, multiplicamos 25 por 8 son 200, lo restamos a 200 y ahora sí, el residuo es 0.

Ahora vamos a dividir 2703 entre 12

Primero, tomo el 27 y lo divido entre 12, el cociente es 2 y sobran 3, le agrego el 0, ahora divido 30 entre 12 el cociente es 2, sobran 6 le agrego el 3, divido el 63 entre 12 el cociente es 5 y sobran 3; lo convierto a decimal y agrego el punto en el cociente, entonces es 30 entre 12 el cociente es 2. Sobran 6 décimos, lo convierto a centésimos y son 60 entre 12, el cociente es 5 y sobran 0.

El resultado de 2703 entre 12 es 2.25

La siguiente división es 1921 entre 25

Vamos a dividir 192 entre 25, el cociente es 7 y sobran 17, agregamos el 1 ahora dividimos 171 entre 25 el cociente es 6, sobran 21 enteros. Para poder seguir dividiendo lo convertimos a decimal y tenemos que agregar el punto al cociente.

Entonces es 210 entre 25, el cociente es 8, sobran 10 décimos; para poder dividirlo, convertimos a centésimos y son 100 entre 25, el cociente es 4 y el residuo es cero.

El resultado es: 76.84

Vamos a resolver la división 1791 entre 12

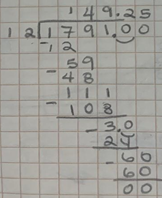
Primero dividimos 17 entre 12 el cociente es 1 y sobran 5, le agrego el 9. Ahora divido 59 entre 12, el cociente es 4, sobran 11 y le agrego el 1. Divido el 111 entre 12, el cociente es 9 y sobran 3; lo convierto a decimal y agrego el punto en el cociente.

Entonces es 30 entre 12 el cociente es 2, sobran 6 décimos, lo convierto a centésimos y son 60 entre 12, el cociente es 5 y sobran 0.

El resultado de 1791 entre 12 es 149.25

La siguiente división es 1067 entre 20

Vamos a dividir primero 106 entre 20, el cociente es 5 y sobran 6. Agregamos el 7, ahora dividimos 67 entre 20, el cociente es 3 y sobran 7 enteros. Para poder seguir dividiendo lo convertimos a decimal y tenemos que agregar el punto al cociente. Entonces es 70 entre 20, el cociente es 3 y sobran 10 décimos. Para poder dividir lo convertimos a centésimos y son 100 entre 20 el cociente es 5 y el residuo es cero, el resultado es 53.35

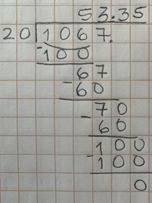
Vamos a dividir 2189/25

Primero divido 218 entre 25, el cociente es 8 y sobran 18. Le agrego el 9 ahora divido 189 entre 25 el cociente es 7, sobran 14. Lo convierto a decimal y agrego el punto en el cociente; entonces, es 140 entre 25 el cociente es 5, sobran 15 décimos; los convierto a centésimos y son 150 entre 25, el cociente es 6 y sobran 0.

El resultado de 2189 entre 25 es 87.56

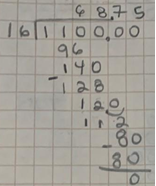
Vamos a dividir 1100 entre 16

Primero voy a dividir 110 entre 16, el cociente es 6 y sobran 14, agregamos el 0 ahora dividimos 140 entre 16, el cociente es 8 y sobran 12 enteros. Para poder seguir dividiendo lo convertimos a decimal y tenemos que agregar el punto al cociente, entonces es 120 entre 16, el cociente es 7. Sobran 8 décimos para poder dividir los convertimos a centésimos y son 80 entre 16, el cociente es 5 y el residuo es cero.

El resultado es 68.75

La siguiente división es: 1722 entre 24

Empezamos dividiendo 172 entre 24, el cociente es 7 y sobran 4. Le agrego el 2, ahora divido 42 entre 24, el cociente es 1 y sobran 18. Ahora convierto a decimal y agrego el punto en el cociente, entonces es 180 entre 24, el cociente es 7. Sobran 12 décimos, los convierto a centésimos y son 120 entre 24, el cociente es 5 y sobran 0.

El resultado de 1722/24 es 71.75

Vamos a dividir 2901 entre 12

Primero divido 29 entre 12 el cociente es 2 y sobran 5, le agrego el 0. Ahora divido 50 entre 12, el cociente es 4 y sobran 2; le agrego el 1, divido el 21 entre 12, el cociente es 1 y sobran 9.  Lo convierto a decimal y agrego el punto en el cociente, entonces es 90 entre 12 el cociente es 7, sobran 6 décimos. Los convierto a centésimos y son 60 entre 12, el cociente es 5 y sobran 0.

El resultado de 2901/12 es 241.75

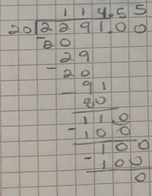
Ahora vamos a dividir 2291 entre 20

Primero divido 22 entre 20 el cociente es 1 y sobran 2; le agregamos el 9, ahora divido 29 entre 20, el cociente es 1; sobran 9, le agrego el 1; divido el 91 entre 20, el cociente es 4 y sobran 11. Convierto el 11 a decimal y agrego el punto en el cociente; entonces es 110 entre 20, el cociente es 5, sobran 10 décimos. Los convierto a centésimos y son 100 entre 20, el cociente es 5 y sobran 0.

El resultado es 114.55

Vamos a resolver la división 1823 entre 16

Primero divido 18 entre 16, el cociente es 1 y sobran 2; le agrego el 2. Ahora divido 22 entre, 16 el cociente es 1 y sobran 6; le agrego el 3, divido el 63 entre 16, el cociente es 3 y sobran 15.  Convierto el 15 a decimal y agrego el punto en el cociente, entonces es 150 entre 16, el cociente es 9 y sobran 6 décimos; los convierto a centésimos y son 60 entre 16, el cociente es 3 y sobran 12.

Para que tengas como residuo 0 es necesario convertir los centésimos a milésimos.

Entonces vamos a dividir 120 centésimos entre 16, el cociente es 7 y nos sobran 8 milésimos. Como todavía no tenemos residuo 0 debemos continuar la división; así que convertimos a diezmilésimos. Entonces dividimos 80 entre 16, el cociente es 5 y el residuo 0.

Este procedimiento: el de analizar los pasos que se siguen para utilizar el algoritmo de la división, es un ejercicio mecanizado que sirve únicamente para analizar los pasos a seguir.

Desde luego, la práctica te permitirá memorizar estos pasos, habrá ocasiones en que necesitemos hacer una división y sólo tengamos a la mano hoja y lápiz, sin embargo, es importante aclarar: el uso del algoritmo de la división es uno de muchos procedimientos o técnicas que ya hemos visto para resolver problemas de división. Por lo que el algoritmo se convierte en una especie de resumen o simplificación de las otras estrategias que hemos usado para la resolución de problemas de división.

En las primeras clases vimos la aproximación o estimación de las cifras del cociente. Buscar la decena o centena más cercana es otra estrategia; o la búsqueda del cociente que al multiplicarse por el divisor, más el residuo, nos da como resultado el dividendo.

Todos estos recursos o procedimientos son tan importantes, o más, que el uso del algoritmo. De lo que se trata en las clases de matemáticas es de resolver problemas de la vida cotidiana, y para ello estamos empleando muchos recursos, herramientas, técnicas y procedimientos.

El día de hoy resolvimos divisiones con decimales utilizando el algoritmo de la división, es importante que en casa sigas practicando estos pasos para resolver operaciones y problemas, recuerda que en el caso de que tengamos un residuo diferente a cero es necesario seguir repartiéndolo y para poder hacerlo se requiere pasar a la unidad siguiente inferior agregando un cero al residuo.

El reto de hoy:

Te invito a resolver el desafío número 25 “Repartir lo que sobra”, que se encuentra en la página 60 de tu libro de Desafíos Matemáticos.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Consulta los libros de texto en la siguiente liga.

https://www.conaliteg.sep.gob.mx/primaria.html

Descarga tu clase dando clic aquí