Números positivos y negativos

Números positivos y negativos

Aprendizaje esperado: consolida contenidos del eje: número, álgebra y variación.

Énfasis: integrar los contenidos de los temas: número y adición y sustracción.

¿Qué vamos a aprender?

En esta sesión consolidarás el aprendizaje esperado, que es Consolida contenidos del eje: número, álgebra y variación.

Se te recomienda que para el desempeño de tus actividades tengas a la mano tu cuaderno u hojas reutilizables, lápiz, goma y sacapuntas. Así como tu libro de texto de la asignatura. En caso de tener una discapacidad visual, prepara hojas leyer, un punzón y una regleta.

Asimismo, prepara todos los aprendizajes adquiridos durante estas sesiones, porque los llevarás a la práctica.

¿Qué hacemos?

Durante esta sesión revisarás una recreación del juego de rally de retos matemáticos con el aprendizaje de la sesión.

En donde imaginarás que hay dos equipos en los cuales participan algunos de tus compañeros.

Primer equipo llamado Coyotes: conformado por: Ana y Julio.

Segundo equipo denominado Jaguares que lo integran Blanca y Alfonso.

Tú en casa puedes imaginar que eres parte de alguno de estos equipos y puedes ir realizando a la par los ejercicios que se les irán presentando a los equipos para que los resuelvan.

Se van a ir dando algunas pistas para los retos, y para que se vaya dando solución.

Cada equipo tendrá un turno de manera escalonada y se tirará un dado para saber cuántas casillas hay que avanzar del tablero, para avanzar en cada casilla cada equipo tendrá que responder a un reto de manera adecuada. El equipo en llegar primero a la meta será el equipo ganador.

Ya elegiste tu equipo. Ahora inicia el juego.

Se comienza y se lanza el dado para saber cuánto se avanza en el tablero. El primer equipo que tira es el equipo de Jaguar. El cual avanza a la casilla 6.

El primer reto que se debe resolver es el siguiente.

Martha preparará un pan, la receta dice que debe utilizar 5/8 de kilogramo de harina. Ella sólo tiene una báscula digital para medir en kilogramos la porción de harina. ¿Cómo podría Martha saber qué cantidad de harina necesita en número decimal?

Blanca dice que, si no se equivoca, debe realizar una conversión de fracción a número decimal y así Martha sólo debe colocar la cantidad adecuada de harina sobre la báscula.

Así es, como dice Blanca, hay que tener presente que un número racional se puede expresar a través de una fracción común, que a su vez se puede expresar como un numero decimal.

Para convertir una fracción a decimal se debe dividir el numerador entre el denominador, es decir, el numerador será el dividendo mientras que el denominador será el divisor.

Del problema anterior, ¿qué números se identifican como dividendo y divisor?

Blanca dice, que si está en lo correcto, para la fracción 5/8, el numerador 5 será el dividendo y el denominador 8 será el divisor. De esta manera se divide 5 entre 8, lo que da como resultado0.625.

Por lo tanto, la expresión decimar de 5/8 es igual al número decimal, 625 milésimos, lo cual quiere decir que la báscula debe marcar 0.625 kilogramos, que es la cantidad de harina que necesita Martha para su pan.

Blanca ha dado solución a este reto de manera acertada. En casa reflexiona sobre la importancia que tiene conocer las dos expresiones de un número racional, tanto la fracción como el decimal.

Ahora, es el turno del equipo Coyote para avanzar. Se tira el dado y avanzan a la casilla 5. El reto de esta casilla es el siguiente:

Jimena fue a la carnicería y pidió 2/3 de kg de carne, al pesar la carne el encargado del lugar le dijo que la báscula marcaba 0.65 kilogramos, que si así se la dejaba. ¿La báscula marcó la cantidad que solicitó Jimena, o fue más o menos carne?

Julio dice, que lo adecuado para este caso sería convertir el número decimal en una fracción, para facilitar la comparación entre los datos del problema.

Como ves, esta es una buena solución, ya que algunas fracciones como 2/3, al convertirlas en un número decimal, resulta un número periódico, lo cual dificulta la exactitud del resultado, por ello, en este caso es mejor realizar la comparación entre fracciones.

Ahora, para convertir un número decimal a una fracción, se colocan las cifras del número decimal sin el punto, en el numerador y como denominador se debe colocar una potencia de diez, que tenga tantos ceros como cifras, hay a la derecha del punto decimal. Por último, se simplifica la fracción a la mínima expresión, siempre que sea posible.

Julio dice, que primero contará el número de cifras decimales de 0.65, de las cuales son 2. Colocará las cifras del número en el numerador, sin el punto, por lo que tiene 65 y como fueron dos cifras decimales, la potencia de 10 de denominador debe tener 2 ceros, por lo que el denominador es 100, quedando la fracción 65 centésimos.

Para simplificar la fracción, se dividirá ambos miembros entre 5, lo cual dará como resultado 13/20, y así queda, porque ya no se puede simplificar más.

Ahora para comparar 13/20 con 2/3 se obtienen fracciones equivalentes para cada una con igual denominador, 13/20 es igual a 39/60 y 2/3 es igual a 40/60.

Entonces, 40/60 es mayor que 39/60, por lo tanto, 2/3 es mayor que 13/20, por lo que la báscula marcó un poco menos de lo que pidió Jimena.

La solución de Julio, ha sido la adecuada. Es importante que, en casa, reflexiones que no todas las fracciones deben convertirse a decimal, por ello es practico también conocer como convertir un decimal a fracción.

Es el turno de los Jaguares. Es momento de saber hasta dónde van avanzar, así que lanzan el dado, esta vez es Alfonso quien lo hace. Han llegado a la casilla 11.

Aquí el reto consiste en que deben encontrar un número de manera que, sumando a 25, dé como resultado el número 14.

Como el resultado es un número menor al sumando conocido, es decir, 14 es menor que 25, entonces se tiene que buscar entre los números positivos y los negativos.

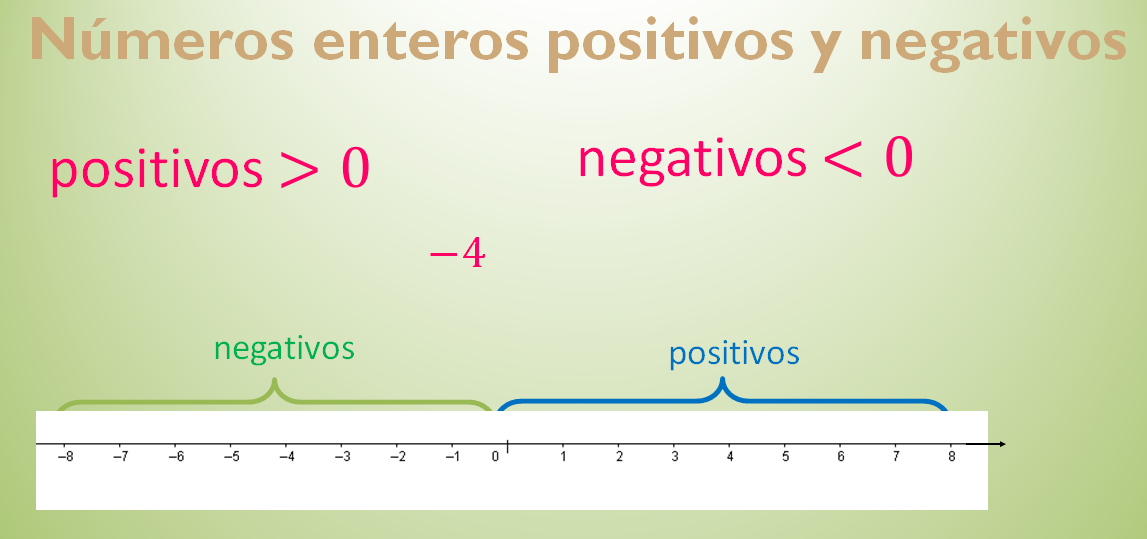
Recuerda que los números enteros se conforman por los números positivos y negativos. Los números positivos son aquellos mayores que cero, mientras que los números negativos son menores que cero y les antecede un signo de menos. Cuando ubicas a los números en la recta numérica, tienes del lado derecho del cero a los números positivos y del lado izquierdo, a los negativos.

Alfonso dice que se le ocurre que puede plantear una ecuación para encontrar la respuesta.

Efectivamente, la ecuación que permite obtener la respuesta es 25 + x = 14.

En casa, ¿ya tienes la respuesta del reto?

Alfonso resuelve la ecuación para responder a este reto.

Para resolver la ecuación se tiene que despejar a la incógnita, en este caso, se resta 25 en ambos miembros de la ecuación, quedando x + 25 – 25 = 14 – 25. Al resolver las operaciones, se tiene que x = 11 negativo.

Para comprobar si la respuesta es correcta, se debe sustituir a la incógnita por el valor encontrado. Pero a Alfonso le parece adecuado en este caso, revisar la regla de la adición de números positivos y negativos.

Cuando se suman dos números positivos o dos números negativos, se suman sus valores absolutos y el resultado conserva el mismo signo de los sumandos, es decir, positivo más positivo es igual a positivo y mientras que negativo más negativo es igual a negativo.

Al sumar un número positivo y uno negativo, se calcula la diferencia entre los valores absolutos y el resultado conserva el signo del número con mayor valor absoluto.

Ahora sí, se puede comprobar el resultado de la respuesta de Alfonso. Si se sustituye a “x” y se tiene la suma 11 negativo más 25.

Al calcular la diferencia entre los valores absolutos, se tiene que valor absoluto de 25 menos valor absoluto de 11 negativo, es igual a valor absoluto de 14 y como 25 tiene mayor valor absoluto, el resultado es un número positivo, es decir, 11 negativo más 25 es igual a 14 positivo.

Excelente respuesta de Alfonso, se espera que, si tú apoyas este equipo en casa, hayas logrado llegar a la misma solución.

Ahora lanzará el dado el equipo de Coyotes. Esta vez el dado cayó y marcó el número 4, es decir, que el equipo llega a la casilla 9.

En este caso Ana es quien resolverá el siguiente reto, que es el siguiente:

Pedro tiene una cuenta de ahorro, y recibió una bonificación por parte del banco de $100. Si su saldo ahora es de $50, ¿cuál era su saldo antes de la bonificación?

Aquí, seguramente te preguntarás, ¿cómo es posible que el saldo de Pedro sea una cantidad menor al bono que recibió?

Pero, debes recordar que, al hablar de saldos a favor o saldos en contra o deudas, se involucran números positivos y negativos. Y si se revisa la regla descrita antes de una operación de números positivos y negativos te permite obtener la respuesta.

Entonces Ana, está buscando un número positivo o negativo que al sumarle 100, de cómo resultado 50 positivo.

Para resolverlo, Ana puede utilizar el siguiente planteamiento donde “x” representa el saldo anterior de Pedro en su cuenta bancaria, a esto se le suman los 100 pesos de bonificación y su suma es igual a 50, que es su saldo actual.

Ahora bien, para encontrar el valor de “x” Ana resta 100 en ambos miembros de la igualdad y obtiene la ecuación x = 50 – 100. Así ella, averigua la cantidad inicial que había en la cuenta.

Únicamente tiene que resolver la resta 50 menos 100, cuyo resultado es 50 negativo. Aplicando las reglas de la adición de números positivos y negativos, se puede comprobar el resultado.

Se calcula la diferencia entre los valores absolutos y como 100 tiene mayor valor absoluto, el resultado es positivo. Por lo tanto 50 negativo más 100 es igual a 50.

Así es, el resultado de Ana al problema es correcta y es conveniente resaltar la importancia del uso de los números enteros positivos y negativos en las cuentas bancarias y la economía.

Bien, es hora de lanzar nuevamente el dado, el turno es de Jaguares, en donde Blanca lanza el dado y cae en el número 6, con lo cual, el equipo se ubica en la casilla 17, están cerca de lograr el triunfo.

El reto es el siguiente:

El filósofo Platón nació 430 antes de nuestra era y murió en el año 349 antes de nuestra era. La pregunta es, ¿a qué edad murió Platón?

Para resolver este problema, hay que reflexionar lo siguiente, ¿qué operación permite calcular la edad de alguien cuando se sabe su año de nacimiento?

Blanca dice que en estos casos suele restar el año actual, al año de nacimiento. Por ejemplo, su prima Norma nació en el año 1985, para saber qué edad tiene, restó 2021 menos 1985, con esta operación sabe que su prima tiene 36 años.

Así es. Pero, en el caso de Platón se puede ubicar en una recta numérica, a los años antes de nuestra era y se representan como negativos, mientras que los años de nuestra se ponen como positivos.

Entonces, el año de nacimiento de Platón se puede expresar como 430 negativo, mientras que el año de defunción se expresa como 349 negativo.

Así, si se aplica lo mismo que hizo para calcular la edad de su prima Norma debe restar 349 negativo menos 430 negativo.

Así es Blanca, para resolver este problema, se tiene que realizar una sustracción de números negativos.

En casa, ¿recuerdas cómo resolver estas operaciones?

Para realizar esta resta se utilizará la regla de la sustracción de números positivos y negativos, la cual dice que restar es lo mismo que sumar por el opuesto o inverso aditivo. Revisa algunos ejemplos.

En la sustracción 11 positivo menos 3 negativo se utiliza el inverso aditivo de 3 negativo que es 3. La adición equivalente a esta sustracción es 11 positivo más 3 positivo y para ambos casos el resultado es 14 positivo.

Para la resta 6 negativo menos 2 negativo, la adición equivalente es 6 negativo más 2 positivo igual 4 negativo.

Y finalmente, 5 positivo menos 4 positivo, cuyo inverso es 4 negativo, su adición equivalente es 5 positivo más 4 negativo, quedando como resultado 1 positivo.

Entonces, para realizar la sustracción de 349 negativo menos 430 negativo, se resuelve la suma 349 negativo más 430, y utilizando la regla de la adición se obtiene 81 positivo. Por lo tanto, Platón murió a los 81 años.

Estos tipos de problemas te ayudan a ver la importancia de la sustracción de números enteros.

Ahora, el equipo de Coyotes, lanza el dado, en este caso Julio es quien lo lanza, y llegan a la casilla 15.

El reto es:

Luis tiene 22 años y su papá 40. ¿En qué momento la edad del papá de Luis fue o será el doble de su edad?

Las dificultades para plantear y resolver este problema en particular. Surgen cuando te enfocas únicamente en que ambos sujetos involucrados cumplirán al año siguiente y así sucesivamente, es decir, el tiempo los afecta por igual. Así que se recomienda ampliar un poco más esta visión.

Julio dice que lo tendrá en cuenta, al momento de buscar la solución, apoyándose en la siguiente tabla.

En la primera columna se encuentra la edad de Luis, en la segunda columna se encuentra el doble de la edad de Luis, mientras que en la tercera columna está la edad del papá. De esta manera se puede comparar cada una de las edades con el paso de los años, tanto los años que están por transcurrir como los años ya transcurridos.

Dice Julio, que conforme pasan los años no encuentra alguna coincidencia que cumpla con la condición del reto.

Es decir, para ninguna edad de Luis la edad de su papá es el doble. Pero, como se pregunta cuándo fue o cuándo será, se regresó algunos años y hay una coincidencia cuando Luis tenía 18 su papá tenía 36 años.

Esa es la solución correcta al problema, aunque es importante que tú conozcas al igual que Julio el planteamiento que da solución a este problema. Pon atención.

Se interpreta la edad de Luis con la ecuación 22 + x, debido a que “x” es el número de años que deben de transcurrir, toda la expresión algebraica será multiplicada por dos, debido a que se necesita que la edad represente el doble.

Para completar la ecuación, del otro lado se representa la edad del papá con 40 + x.

Para resolver la ecuación, primero se va a aplicar la propiedad distributiva en la edad de Luis al multiplicar 2 por 22, y 2 por “x”, así se obtiene 44 + 2x después se agrupan los términos semejantes, del lado izquierdo se encuentran las incógnitas.

Aplicando la propiedad uniforme de la igualdad se tiene 2x -x +44 – 44= x -x +40 -44, al simplificar se obtiene la ecuación 2x-x =40 -44 ahora sólo debes de reducir los términos semejantes. Restando 2x-x igual a “x”, y restado 40 menos 44 igual a 4 negativo.

De esta manera, se comprueba el resultado de la ecuación con el obtenido por Julio y es el mismo. Es decir, hace 4 años, cuando Luis tenía 18 años, la edad de su papá era el doble, 36.

Nota: Los problemas mostrados sobre números enteros forman parte de una investigación realizada por Gallardo en 1994, pionera en México en el estudio de los números negativos.

Bien después de revisar esta información, el equipo de Jaguares, representado esta vez por Alfonso tira el dado y llega a la última casilla que es el número 18. Así que solo falta resolver el reto de esta casilla.

El reto es: un submarino sigue una ruta de exploración; primero desciende 1.3 metros, posteriormente desciende 2.47 metros, por último, asciende 2.91 metros. ¿A qué profundidad se encuentra el submarino?

Alfonso tiene la inquietud de que, si cuando se menciona que el submarino está descendiendo, se hace referencia a un número negativo, cuando se habla del nivel del mar se hace referencia al 0 y si los positivos, están por encima del nivel del mar o de un ascenso.

Lo cual, es tal como lo describe. Tanto Alfonso como tú, deben tener presente que, al momento de operar con números decimales, se aplican las mismas reglas de la adición de números enteros positivos y negativos.

Así que, siguiendo las indicaciones, Alfonso primero identificó los números positivos y negativos.

Primero descendió 1.3 representado como 1.3 negativo, posteriormente vuelve a descender 2.47 metros, es decir, 2.47 negativo, por último, asciende 2.91 metros, es decir, 2.91 positivo. Ahora, hay que representar la adición. Primero se suman los números negativos.

Al sumar 1.3 negativo y 2.47 negativo da como resultado 3.77, al ser ambos negativos el resultado también es negativo. Ahora, para sumar 3.77 negativos más 2.91, obtuvo la diferencia entre los valores absolutos de los sumandos, y como el número con mayor valor absoluto es 3.77 negativo, quiere decir que el resultado es 0.86 negativo. Por lo tanto, la profundidad del submarino es de menos 0.86 metros.

Con esta solución que dio Alfonso, se ha logrado la victoria de Jaguares.

El reto de hoy:

Para ampliar la información que viste en esta sesión, puedes revisar más sobre el tema en tu libro de texto o consultar con tu profesora o profesor a distancia.

Asimismo, concluye tus ejercicios que se realizaron en el desarrollo de la sesión, en caso de que te hayan quedado pendientes.

¡Buen trabajo!

Gracias por tu esfuerzo.

*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html