Números decimales en la recta numérica y su equivalencia con una fracción decimal
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 16:42Números decimales en la recta numérica y su equivalencia con una fracción decimal
(Clase de repaso)
Aprendizaje esperado: convierte fracciones decimales a notación decimal y viceversa. Aproxima algunas fracciones no decimales usando la notación decimal. Ordena fracciones y números decimales.
Énfasis: ubicar números decimales en la recta numérica, comparar números decimales y determinar la equivalencia de cualquier fracción con una fracción decimal.
¿Qué vamos a aprender?
En esta lección analizarás cómo ubicar números decimales en la recta numérica, compararás números decimales entre sí, para determinar cuál de ellos es mayor, menor o si son iguales y verás cómo establecer la equivalencia de una fracción común con una fracción decimal.
¿Qué hacemos?
A propósito del tema de hoy, es increíble lo rápido que crecen los adolescentes. Seguramente lo has notado. Si
no, haz la prueba de medirte semana a semana y registra las medidas que vas obteniendo, para que observes cómo vas creciendo.
Un recurso que puedes utilizar para llevar el registro es el de anotar tus medidas en una recta numérica. Sin embargo, el crecimiento de una semana a otra será apenas de unos milímetros, así que tendrás que aprender a ubicar números decimales en la recta numérica, ya que posiblemente obtendrás medidas como: uno punto cincuenta y tres metros, uno punto sesenta y un metros, etcétera.
Para ayudarte a realizar dicho registro de una manera adecuada pon atención al siguiente ejemplo:
Para ubicar el número decimal siete décimos (0.7) en la recta numérica se puede seguir el siguiente procedimiento:
- Dado que siete décimos nos indica por su expansión decimal que en una unidad hay diez décimos. Para ubicarlo en la recta numérica podemos dividir la unidad en diez partes iguales.
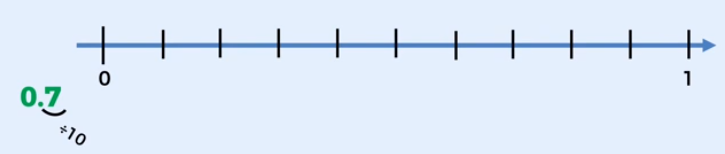
- Ya sabes que hay números positivos y negativos, y cómo ubicarlos en la recta numérica
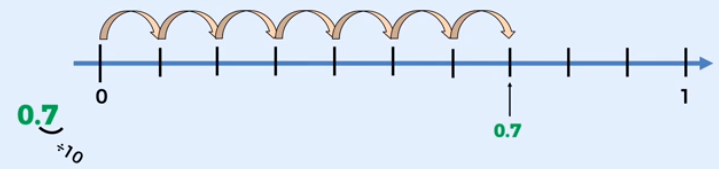
En este caso, siete décimos es un decimal positivo, y se ubica a la derecha del cero. - Para ubicar siete décimos en la recta nos vamos a mover a partir del cero siete posiciones a la derecha, empezando con uno, dos, tres, cuatro, cinco, seis, siete; como observas siete décimos se ubican en este punto de la recta numérica.
En el caso del número sesenta y tres centésimos (0.63) identificamos que es un número decimal del orden de los centésimos, esto significa que la unidad está dividida en cien partes iguales.
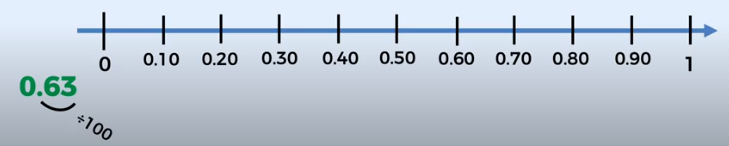
En este ejemplo, como en el anterior, no hay un número entero, es decir estamos entre cero y uno. Vamos a dividir en cien partes iguales la distancia entre cero y uno, primero dividiremos en diez segmentos iguales y a su vez cada segmento resultante también lo subdividimos en diez partes iguales.
Así que partiendo del cero tenemos que llegar al cero punto sesenta y tres centésimos. Es decir, nos movemos uno, dos, tres, cuatro, cinco, seis posiciones y ahora tres centésimos está entre seis décimos y siete décimos es decir el cero punto sesenta y tres centésimos se encuentra en este lugar.
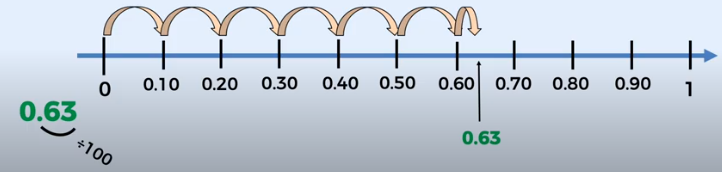
¿Te diste cuenta por qué, en la recta numérica, del cero al uno se dividió en diez partes iguales?
Repasemos el nombre que recibe cada número después del punto decimal de acuerdo con su posición. Para recordar esto, observemos la siguiente imagen:

En esta imagen se muestra el nombre de los números decimales de acuerdo a su posición, en este caso:
- La primera posición a la derecha del punto decimal, donde está el número 5 corresponde a los décimos.
- Siguiendo el mismo orden, en la segunda posición, donde está el número 3, corresponde a los centésimos.
- En la tercera posición, donde está el número 7, corresponde a los milésimos.
- En la cuarta posición, donde está el número 1, corresponde a los diezmilésimos.
- En la quinta posición, donde está el número 6, corresponde a los cienmilésimos.
- Y por último en la sexta posición en donde se encuentra el número 4, corresponde a los millonésimos.
Es importante mencionar que hay más posiciones en los números decimales.
Ahora que recordamos estos nombres, vayamos con un ejemplo de cómo ubicar los registros que vayas obteniendo de tu estatura en la recta numérica; cuyos valores corresponden a números decimales. Por ejemplo: Uno punto cincuenta y dos metros (1.52 m )
La estatura corresponde a un número decimal que significa: un entero con cincuenta y dos centésimos.
Para ubicar este número decimal debemos trazar una recta numérica, que en nuestro caso está dividida del 0 a 10, e identificar entre qué números enteros se encuentra el número 1.52.

Seguramente ya te disté cuenta que “un entero cincuenta y dos centésimos” se encuentra entre el uno y el dos.

De acuerdo con este ejemplo, para ubicar los 52 centésimos debemos dividir en 100 partes iguales la distancia entre 1 y 2, en donde cada división corresponde a una centésima parte de esa distancia.

Contemos centésimo por centésimo a partir del uno hasta llegar a cincuenta y dos centésimos. Por lo tanto, el número decimal uno punto cincuenta y dos queda ubicado en este punto.
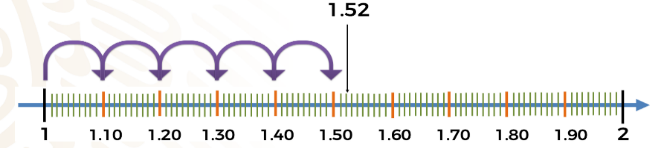
Intentémoslo una vez más, ahora con un metro con setenta y tres centímetros (1.73m). Usemos la recta numérica para ubicar este punto. Recuerda que uno punto setenta y tres es un número decimal que significa: un entero con setenta y tres centésimos. Para ubicar este número en la recta numérica, primero debemos observar entre qué números enteros se encuentra. Al igual que en el ejemplo anterior: un entero con setenta y tres centésimos es mayor que uno, pero menor que dos, por eso se encuentra entre el uno y el dos en la recta numérica.

Siguiendo con este ejemplo, para ubicar los 73 centésimos debemos dividir en cien partes iguales la distancia que hay del uno al dos, en donde cada división corresponde a una centésima parte. Ahora contemos centésimo por centésimo a partir del uno hasta llegar a 73 centésimos. Por lo tanto, el número decimal uno punto 73 queda ubicado en este punto.

Un entero con setenta y tres centésimos es mayor que uno, pero menor que dos. Esto significa que podemos hacer una comparación entre ambos números, para entenderlo mejor, pon atención al siguiente ejemplo:
Para comparar números ya sean enteros o con decimales se tiene que verificar digito por digito empezando con el de mayor orden en su posición decimal, es decir el que se encuentra hasta la izquierda. Así es como se puede saber qué número es mayor, menor o igual con respecto a otro.
Entonces en este ejemplo se están comparando los números 1.40 y 1.04, así que comparando sus dígitos de izquierda a derecha empezando con 1.40 se tiene al 1 y en 1.04 también. Así que por tener el mismo dígito son iguales hasta el momento.
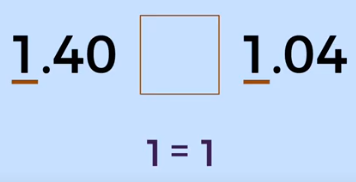
Luego se compara el siguiente dígito a la derecha, en 1.40, es el 4, y en 1.04, es el 0, aquí se sabe que 4 es mayor que 0, y ya encontramos una diferencia entre los dígitos que estamos comparando.
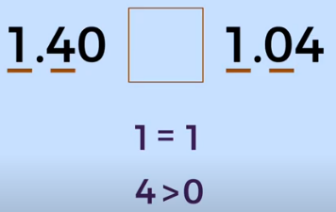
Entonces se sabe que 1.40 es mayor que 1.04.
Podemos hacer comparaciones entre números, por ejemplo: uno entero treinta centésimos 1.30 es mayor que un entero tres centésimos 1.03.
¿Te diste cuenta de que entre los dos números decimales se empleó la frase: mayor que para comparar estos dos números?
A esa frase le corresponde un símbolo que nos sirve para comparar dos cantidades.

La apertura más grande indica el número mayor y la unión indica el número menor. Con lo que acabas de ver, ahora realiza la comparación entre los dos números que ubicamos al principio en nuestra recta numérica: “1.73 metros y 1.52 metros”
1.73 es mayor que 1.52, “un punto setenta y tres es mayor que uno punto cincuenta y dos”.
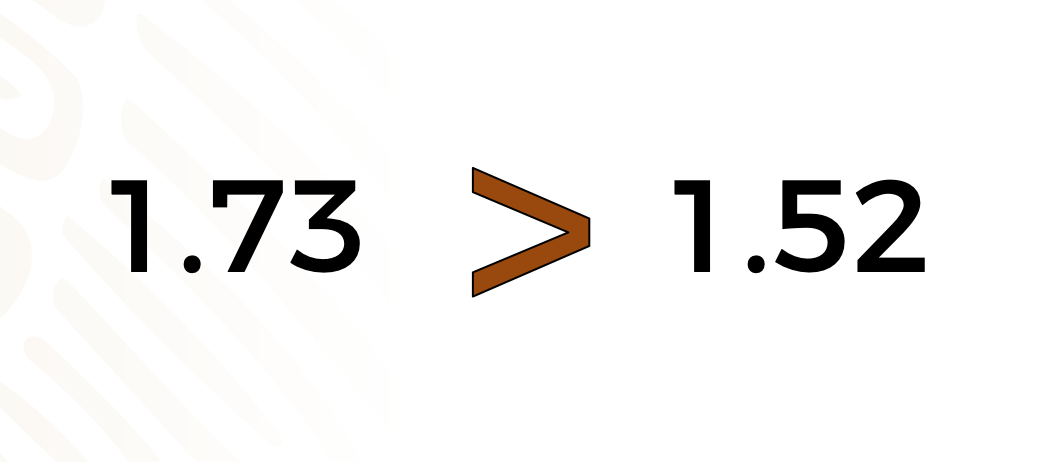
¿Qué pasaría si cambiamos el orden de los números y los comparamos nuevamente?
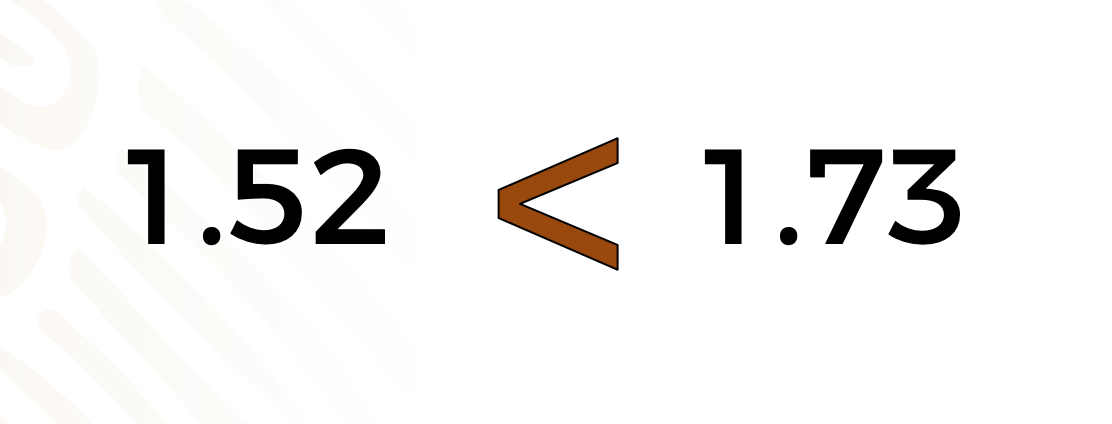
Al comparar estos números, el de la izquierda es de menor orden de magnitud con relación al de la derecha. Entonces podemos afirmar que: “uno punto cincuenta y dos es menor que uno punto setenta y tres”.
¿Y, entonces, cómo distinguimos que dos números son iguales?
Vamos a comparar a 0.320 con 0.32, Observemos que la parte entera únicamente tiene un dígito y es cero. Entonces empezando a comparar dígitos de izquierda a derecha tenemos a cero de un lado y cero del otro lado, donde cero es igual a cero.
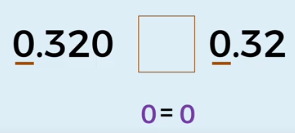
Luego pasamos a la parte de los decimales, aquí está el punto decimal y comparando la primera posición a la derecha del punto decimal se tiene en el primer número un 3 y en el segundo también, llegando a otra igualdad.

Ahora pasamos a la siguiente posición, en el primer número se tiene un 2 y en el otro también, así que continuamos con las igualdades entre los dígitos.
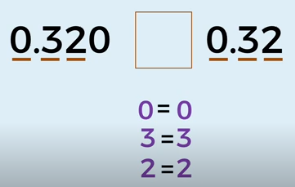
Finalmente, en la tercera posición del primer número se tiene un dígito cero, pero se observa que en la del segundo número no tenemos dígito, en estos casos hay que agregar un cero para tener la misma cantidad de dígitos en la parte decimal y así poder comparar los números.
Una vez que tengamos nuestra tercera posición decimal en el segundo número podemos compararlos de nuevo.

Llegamos nuevamente a una igualdad ya que cero es igual que cero y se concluye después de comparar todos los dígitos de ambos números que: son iguales.
Analizando todo lo anterior, podemos concluir que hay tres símbolos que nos permiten comparar dos números.
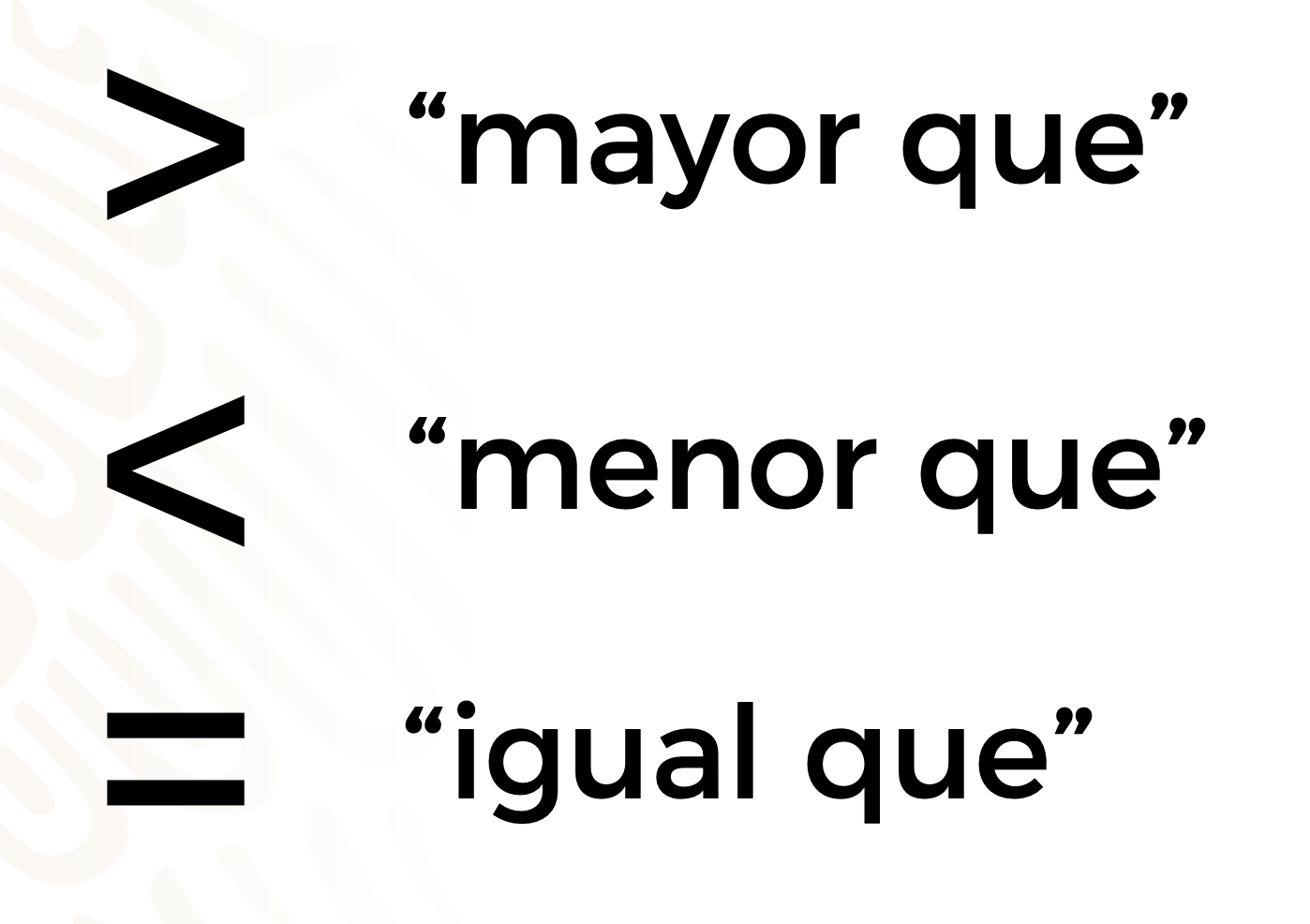
Recuerda que, al comparar dos números decimales, estos deben tener la misma cantidad de cifras antes y después del punto decimal.
En caso contrario, podemos agregar tantos ceros sean necesarios a la izquierda o a la derecha del número, esto no cambiará su valor.
Veamos un ejemplo de la vida cotidiana en el que, sin darnos cuenta, invariablemente, realizamos comparaciones entre cantidades que representan un número decimal.
Te has fijado que los productos alimenticios deben tener una tabla de información nutricional, la cual refiere al valor energético y los nutrientes que contienen, como proteínas, vitaminas, grasas, etc.
Aprovechemos esta información para comparar productos similares y determinar cuál es el que más nos beneficia. Veamos ejemplo de estas tablas:
En esta tabla se muestra la composición nutricional de dos productos: el arroz integral y el refinado.
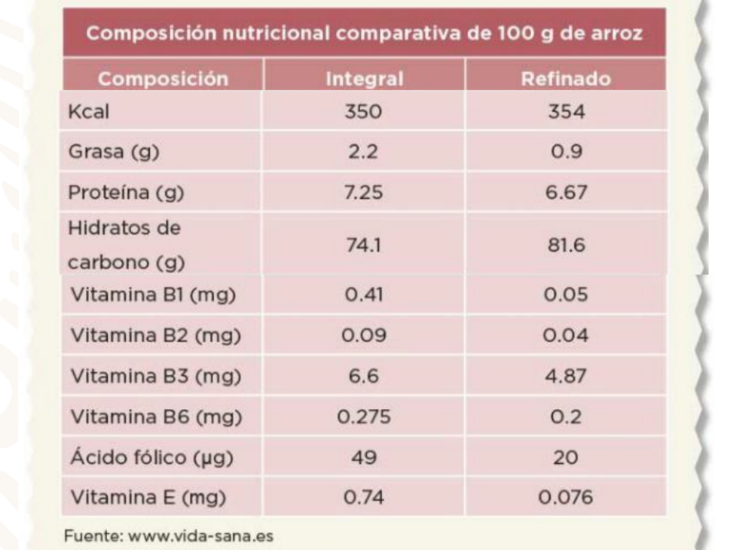
Como todos los productos, estos contienen varios nutrientes, entre los más importantes podemos destacar las vitaminas, ácido fólico y las proteínas.
De acuerdo con la tabla, podemos comparar los nutrientes entre el arroz refinado y el arroz integral, por ejemplo:
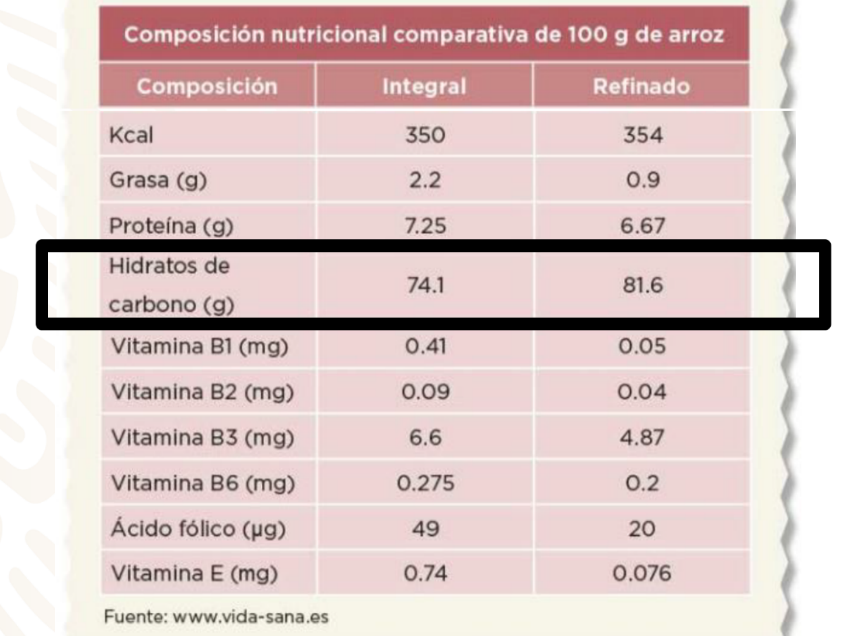
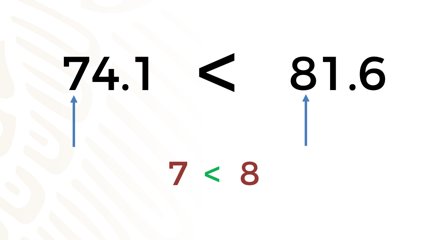
Los hidratos de carbono que contiene el arroz integral son 74.1 gramos y del arroz refinado son 81.6 gramos. Ambas cantidades están representadas con números decimales, por lo tanto, podemos determinar cuáles productos tienen mayor, menor o igual valor, de acuerdo con lo que hemos visto.
En este caso la cantidad de dígitos que tienen los dos números en la parte entera y decimal es la misma, por lo que únicamente comenzaremos a comparar de izquierda a derecha, comenzando con los números: 7 y 8, observen que 7 es menor que 8, por lo que ya no es necesaria otra comparación y se determina que 74.1 es menor que 81.6.
Ahora, si comparamos la Vitamina B6 de ambos productos, ¿el arroz integral tendrá mayor, menor o igual cantidad de este nutrimento?
De acuerdo con los datos de la tabla, el arroz integral contiene 0.275 miligramos y el arroz refinado contiene 0.2 miligramos.

En este caso los dígitos en las dos cantidades no son los mismos, de acuerdo con lo visto anteriormente, se deben complementar agregando dos ceros a la derecha del segundo número para poder hacer la comparación.
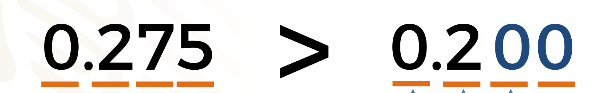
Comencemos a comparar de izquierda a derecha. Analizando los números que están en la posición de las unidades. Vemos que en los dos números hay un cero, por lo que son iguales.
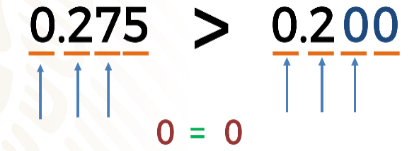
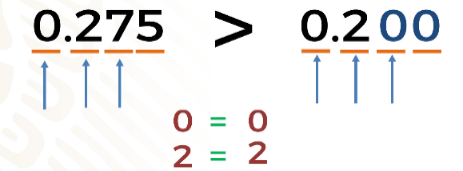
Ahora analicemos los números que están en la posición que corresponde a los décimos el cual es el mismo número, dos.
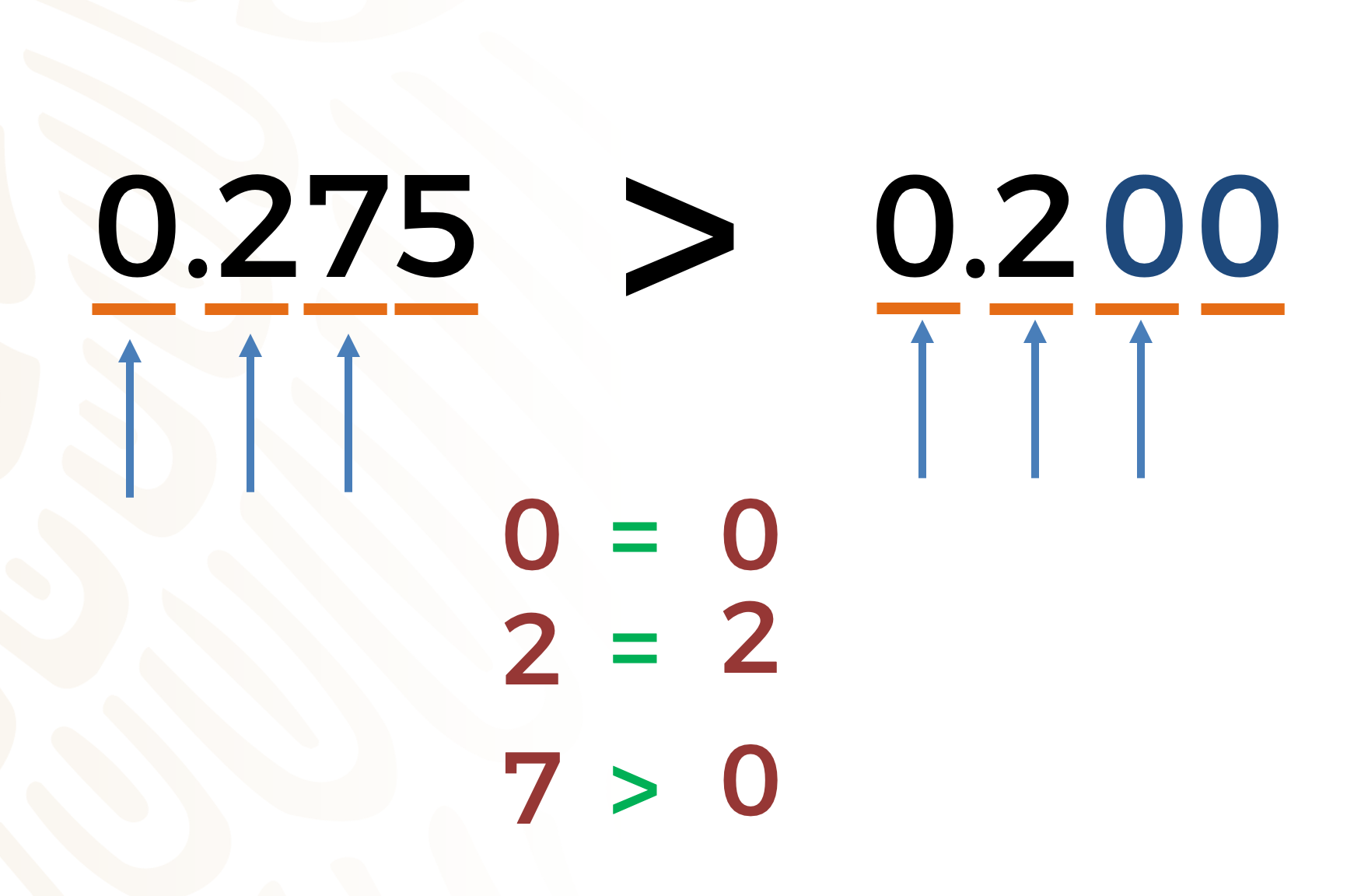
Al ser iguales continuemos con la comparación de los centésimos, donde siete es mayor que cero, concluyendo que: cero punto doscientos setenta y cinco es mayor que cero punto dos.
Así como hicimos la comparación del valor nutricional, con estos dos ejemplos, te invitamos a que lo hagas con otros productos que tengas a tu alcance.
En tu libro de texto de Matemáticas I podrás encontrar otros ejemplos similares a este tipo de comparaciones.
A propósito de los productos que comparamos, ¿te has fijado que cuando has ido a comprar tortillas y pides, por ejemplo, medio kilogramo, el despachador coloca en la báscula quinientos gramos? Esto es porque medio kilogramo es equivalente a quinientos gramos.
Lo mismo sucede si pedimos un cuarto de kilogramo de tortillas, el despachador coloca la báscula en doscientos cincuenta gramos. Al ser equivalentes, podemos emplear dos representaciones distintas para referirnos al mismo valor.
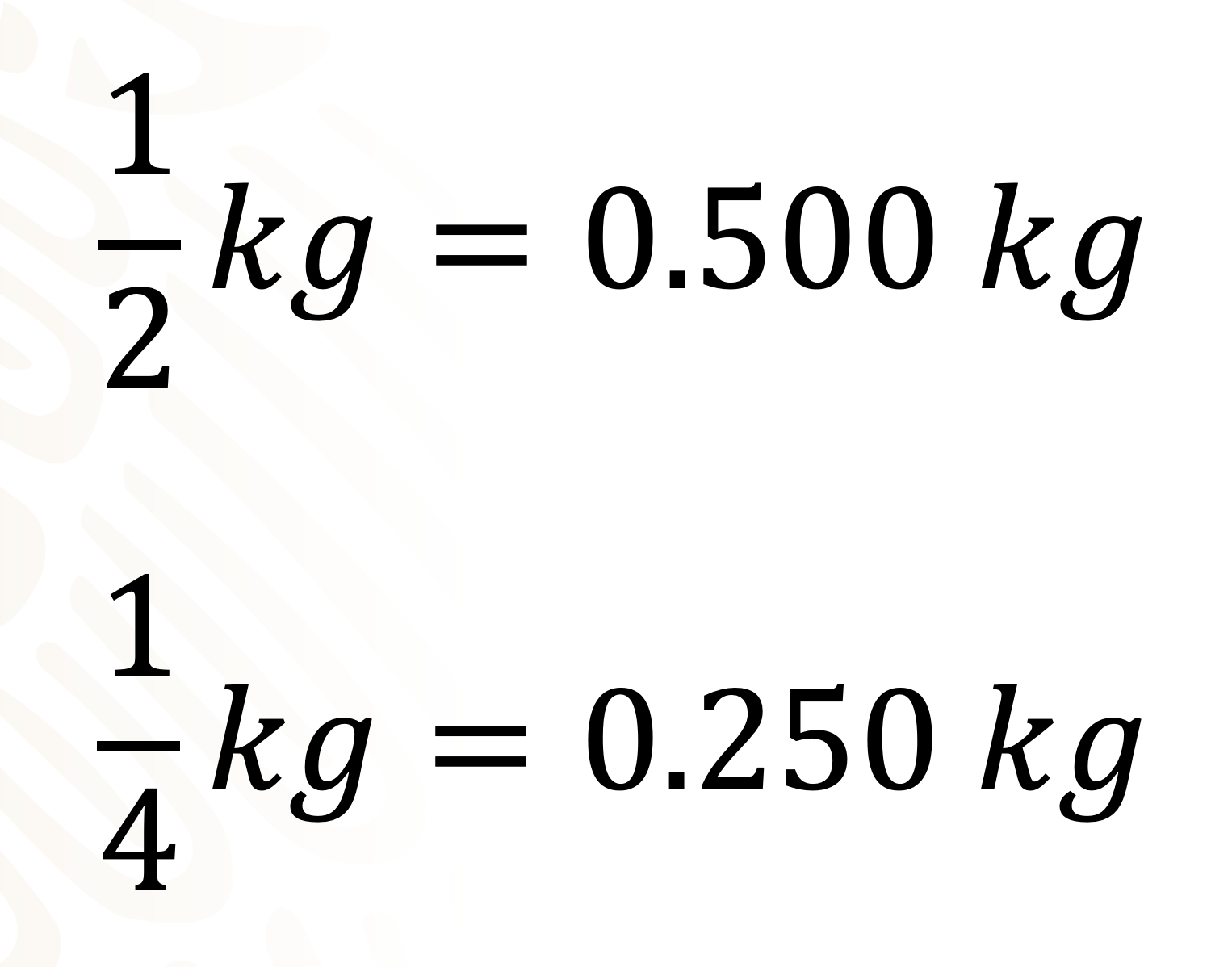
Esto quiere decir, que medio kilogramo es equivalente a cero punto quinientos kilogramos y un cuarto de kilogramo a cero punto doscientos cincuenta kilogramos. Al ser equivalentes, podemos emplear dos representaciones distintas para referirnos al mismo valor.
Existe equivalencia entre números decimales y fraccionarios, y también entre fracciones. Como observarás en el siguiente video del minuto: 03:01 a 03:59
- De fracción común a fracción decimal y viceversa
https://www.youtube.com/watch?v=ygMXQCQlBg8&feature=youtu.be
Las fracciones comunes son equivalentes a una fracción decimal. Estas fracciones se caracterizan porque al dividir el numerador entre el denominador, en algún momento se obtiene un residuo de cero.
Como observamos en el ejemplo, tres cuartos es equivalente a cero punto setenta y cinco, y este número decimal se lee: “setenta y cinco centésimos”, y esto nos da la clave para escribir en el numerador el setenta y cinco y en el denominador el cien.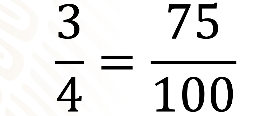
Así, tres cuartos es equivalente a setenta y cinco centésimos. Entonces, setenta cinco centésimos es una fracción decimal, porque el denominador es una potencia de 10.
Esto quiere decir que todas las fracciones que tienen un denominador representado con una potencia de 10 son una fracción decimal.
Por ejemplo: 3 décimos, 12 centésimos, 345 milésimos, 69 diez milésimos, etc.
Entonces, ¿podremos afirmar que cualquier fracción es equivalente a una fracción decimal? Para resolver esta duda observa el siguiente video del minuto: 03:49 a 04:36 - Tipos de fracciones y decimales
https://www.youtube.com/watch?v=CDnq-63F_Tg&feature=youtu.be
Hay fracciones que no tienen equivalencia con una fracción decimal porque al dividir el numerador entre el denominador, el resultado es un número decimal infinito, en consecuencia, no se obtiene un residuo de cero. Por lo que podemos concluir que las fracciones que se representan con un número decimal finito tiene una fracción decimal equivalente.
El reto de hoy:
Te proponemos un juego, que servirá para fortalecer uno de los temas que revisaste hoy: comparación de números decimales.
El juego se llama: “¿Quién forma el número más grande?
Este juego es para dos personas y es necesario que tengas un dado de seis caras, tu cuaderno o una hoja donde puedas escribir.
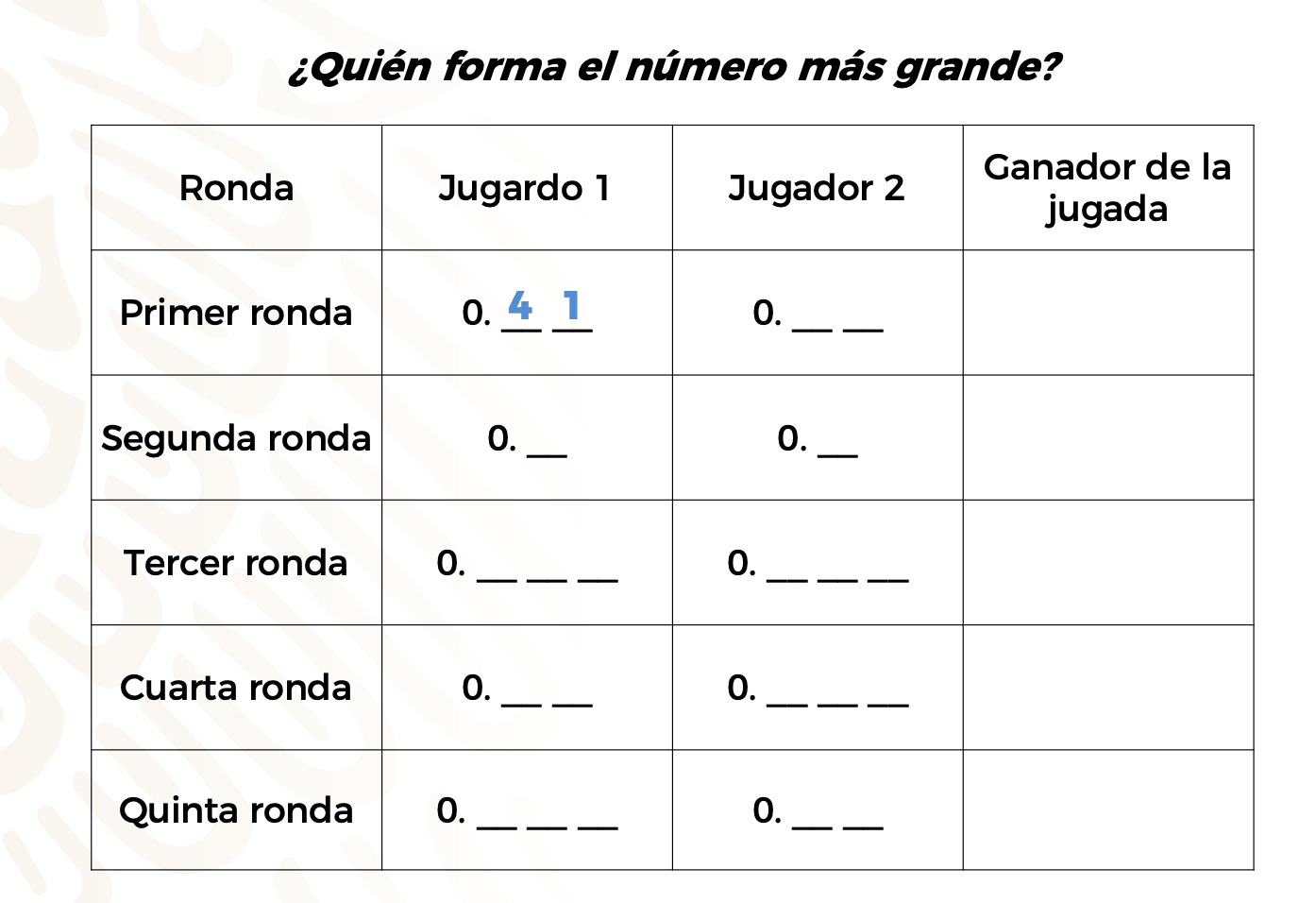
Ahí dibujarás una tabla similar a la que se muestra en la siguiente imagen:

En la que podemos observar cuatro columnas y seis renglones, en la primera columna tenemos de la primera a la quinta ronda, en la segunda columna está el primer jugador con sus respectivas rondas, de igual manera en la tercer columna, para el segundo jugador con sus respectivas rondas y en la última columna debemos ubicar al ganador de cada jugada. Es necesario aclarar que en la segunda y tercera columna tenemos unos espacios que debe llenar cada jugador.
Observa que hay un cero y un punto, seguidos de uno, dos o tres espacios.
Tiren el dado tantas veces como espacios haya y anoten el número que caiga en el espacio que corresponde conforme realizan cada lanzamiento para que cada quien forme un número decimal. Después deberán comparar ambos números y gana la ronda el que forme el número decimal mayor.
Por ejemplo, el jugador 1, en su primer lanzamiento de dado cae cuatro, este número lo debe anotar en el primer espacio.

En su segundo lanzamiento el dado cayó con el número uno, este se anota en el segundo espacio, formando el número 0.41
Después el jugador 2 en su primer lanzamiento el dado cae en el número cuatro, y en el segundo cae en seis; forman el número 0.46, y se registra en la tabla.
Ahora comparamos los números:

Como puedes observar el número que formó el jugador 2 es mayor que el del jugador 1, por lo que el jugador 2 es el ganador de la primera ronda.

Anímate a seguir con el juego y ganará quien más rondas gane.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más.
Lectura





Login to join the discussion