Número

Número

Aprendizaje esperado: concebir a las matemáticas como una construcción social en donde se formulan y argumentan hechos y procedimientos matemáticos.

Énfasis: vincular conceptos fundamentales.

¿Qué vamos a aprender?

Los materiales que necesitarás son tu cuaderno, lápiz y goma.

Anota en tu cuaderno cualquier idea o inquietud que surja al resolver las situaciones que se estudian.

Alguna vez te has preguntado, ¿cómo y cuándo surgieron las matemáticas?, es decir, ¿quién inventó las matemáticas, ¿cómo y por qué aparecieron los números?, ¿siempre se han representado igual?

Además, sabes que hay diferentes tipos de números como los números naturales, los enteros, los racionales e irracionales.

Conocerás el origen de las matemáticas a través de la historia de los números.

¿Qué hacemos?

La idea de número aparece desde que el ser humano tuvo la necesidad de contar, lo que significa que relacionaba los objetos que tenía, por ejemplo, algunas frutas o pieles de animales, con un concepto en su mente que le permitiera representar cantidades. Por ello comenzó a utilizar diferentes símbolos para representar a los objetos y así facilitar su manejo y comprensión.

Uno de los descubrimientos arqueológicos relacionado con el origen de la actividad de contar y su representación, se encontró en África, en 1960. Se trata del peroné de un babuino.

El babuino es un primate cuyo hábitat natural es la sabana africana. Este peroné de babuino es un hueso largo de la pata. A este descubrimiento arqueológico se le conoce como el hueso de Ishango, y su importancia radica en lo siguiente:

El hueso mide unos 14 centímetros de largo, y presenta una serie de rayitas talladas divididas en tres columnas. Algunos científicos piensan que esas rayitas son la prueba contundente del inicio de la actividad de contar. Así cada una de las muescas o rayas representaba un objeto, probablemente cuántos animales habían cazado o el número de integrantes de una tribu determinada que vivió hace 20,000 años. A lo mejor y cada raya representaba los días que transcurrían entre una salida de Sol y otra consecutivamente.

Entonces ese hueso de Ishango era una herramienta para contar.

Aunque, no todos los científicos piensan que sólo era una herramienta para contar, otros han sugerido que las agrupaciones de rayitas indican un conocimiento matemático más complejo.

Los historiadores de las matemáticas piensan que los números naturales surgen en esas épocas y que cada grupo de personas los representaba de muy diferentes formas usando rayitas o algún otro símbolo.

Hoy a los números naturales, que son los números que se utilizan para contar, se les representa con los símbolos que la cultura árabe aportó y que, como sabes, se escriben de la siguiente manera.

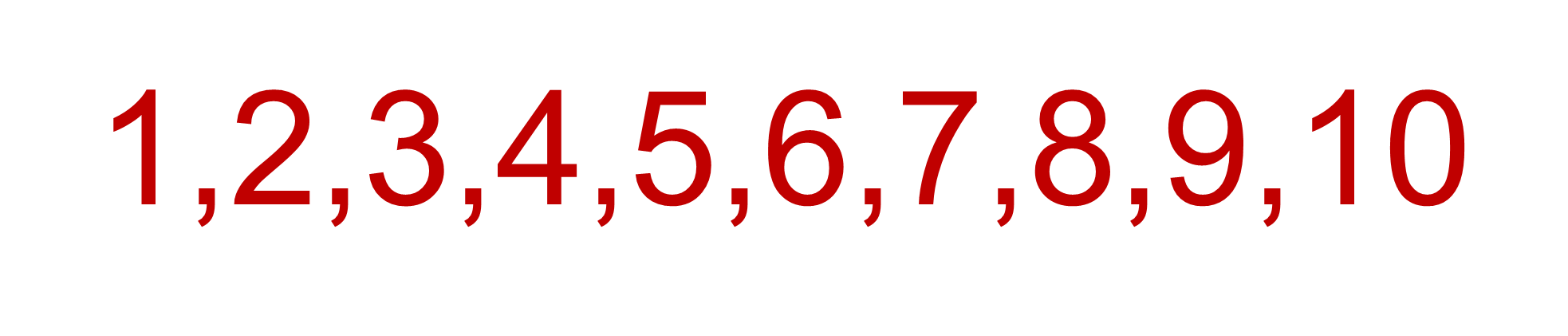
En esta representación de los números naturales no aparece el cero como número natural individual.

El cero no aparece como número natural, aunque esto no significa que no existiera desde aquellos tiempos, es sólo que, en particular, los árabes no lo incluyeron, pues no lo consideraban natural.

Cada cultura creó sus propios símbolos para representar números. Algunos sistemas de numeración son:

El sistema de numeración maya, el sistema de numeración romano, el chino, el indio y el egipcio.

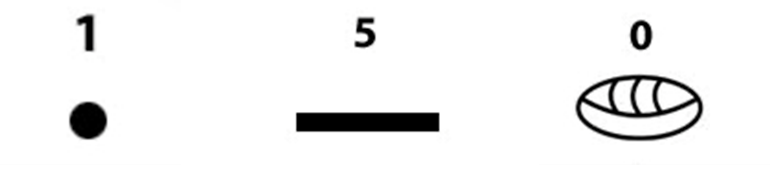
El sistema de numeración maya forma parte de nuestra cultura, por lo que es muy importante conocer alguna de sus características. Es un sistema posicional que utiliza rayas, puntos y una especie de concha. ¿Recuerdas el valor de cada uno de estos símbolos?

El punto representa a la unidad, la rayita horizontal representa al número cinco y la concha es el número cero

Ahora conoce el sistema de numeración romano, el cual utiliza algunas letras mayúsculas como símbolos para representar ciertos valores. Está basado en un sistema posicional y aditivo, lo que significa que cada signo representa un valor que se va sumando al anterior. Posteriormente también restó algunos signos, en lugar de sumar.

Por ejemplo, el número once que se representa con una equis y con una “i” latina. Y aunque parece que ya casi no se utilizan, los puedes ver a diario en la carátula de un reloj.

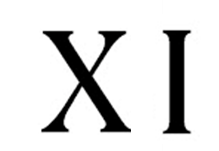
El sistema de numeración egipcio es interesante saber que esta milenaria cultura, desde el año dos mil antes de nuestra, resolvieron problemas cotidianos como la distribución del pan, la construcción de las pirámides o las medidas utilizadas para estudiar la Tierra mediante operaciones que implican fracciones.

Entonces, además de los números naturales, también conocían y utilizaban números fraccionarios.

Uno de los documentos más antiguos que contiene problemas matemáticos es el papiro de Ahmes. En él se encuentran 87 problemas matemáticos, varios de ellos de operaciones con fracciones.

Los antiguos egipcios hicieron cálculos usando fracciones unitarias como un medio, un tercio, un cuarto, un quinto, es decir, fracciones que tienen como numerador el uno, pero en aquella época se representaban de otra manera.

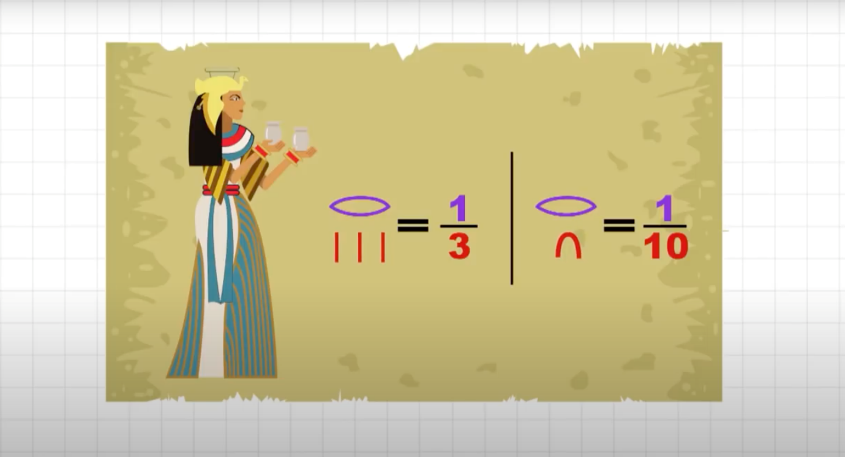
Los egipcios tenían una escritura basada en jeroglíficos, el que tenía forma de boca abierta era el numerador y un jeroglífico numérico escrito debajo de la boca abierta era el denominador de la fracción.

Pero antes de continuar con el desarrollo de los números en su forma decimal, termina de revisar a los números naturales.

Una vez que aparecieron los números naturales, las personas además de contar ya podían realizar cálculos. Con los números naturales ya se podían realizar operaciones básicas como suma, resta, multiplicación o producto y división.

Los números naturales son un conjunto ordenado e infinito de números que cumplen, con respecto a las operaciones básicas de suma y multiplicación o producto, una propiedad muy importante llamada propiedad de cerradura.

La propiedad de cerradura nos dice que:

Y que:

Eso significa que si sumas, por ejemplo, el número natural treinta y cinco más el número natural cuarenta, el resultado es setenta y cinco, que también es un número natural.

Y que, si realizas el producto de veinte, que es un natural, por cuatro, que también es un natural, el producto es ochenta, y también es un número natural.

¿Por qué en los números naturales la propiedad de cerradura no funciona para las operaciones de resta y división?

La respuesta será a través de un ejemplo, resuelve la siguiente resta:

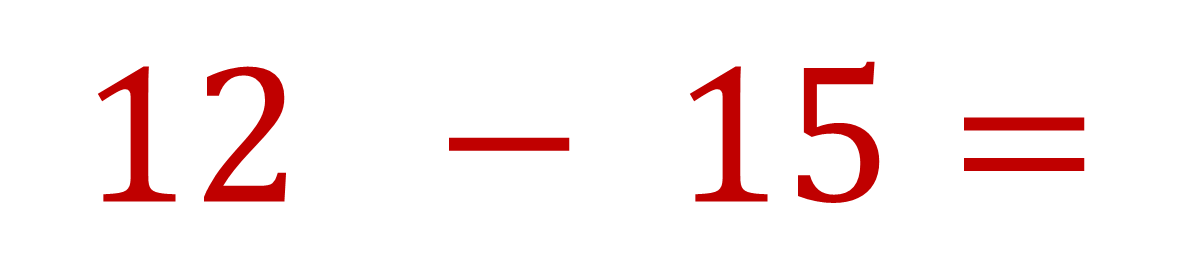
El resultado es negativo tres.

Ahora piensa, negativo tres, ¿es un número natural?

Por supuesto que no, negativo tres es un número, es un número entero negativo.

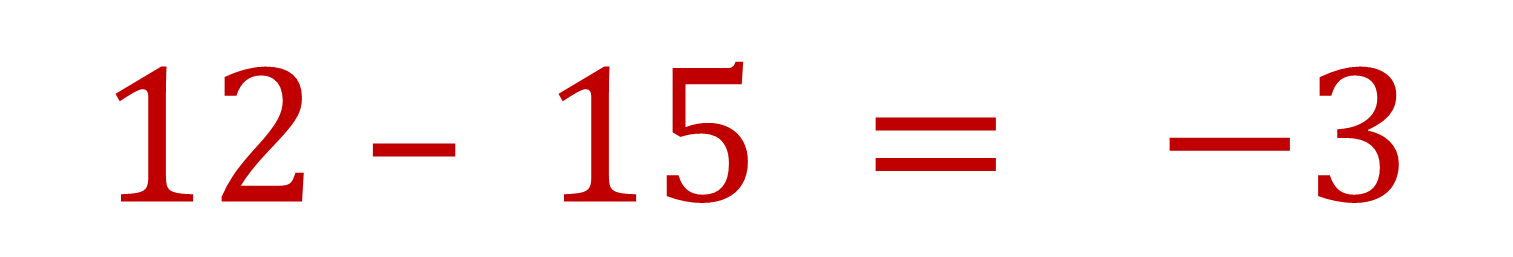
Y por lo tanto la propiedad de cerradura no se cumple en la resta de números naturales.

Ahora revisa la operación de división. Comprueba que la propiedad de cerradura no se cumple para la división en los números naturales.

Por ejemplo, el número natural nueve, entre el natural doce, da como resultado cero punto setenta y cinco, que no es un número natural, es un número decimal.

La división no cumple con la propiedad de cerradura en todo el conjunto de los números naturales.

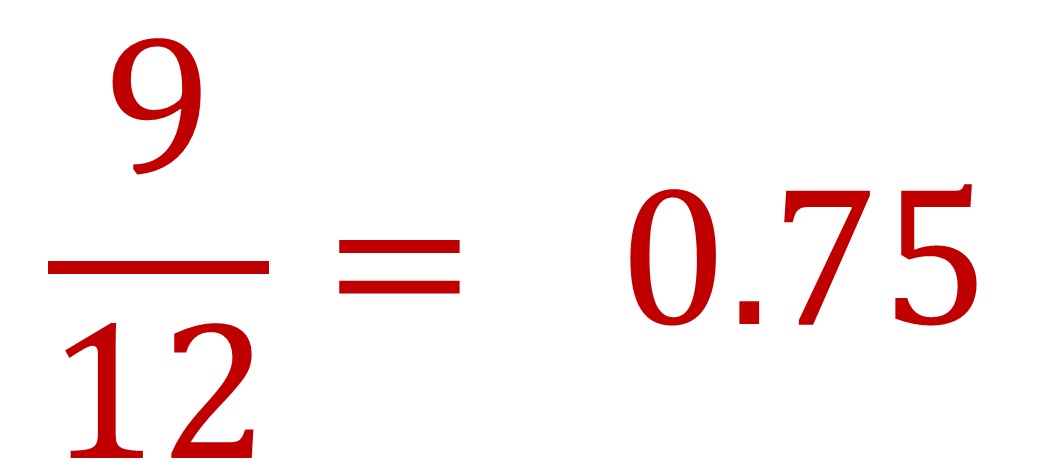
Revisa los sistemas de numeración chino e indio, y al mismo tiempo, su aporte a la representación de los números negativos, los cuales forman parte del conjunto de los números enteros.

Observa el siguiente video, pero antes piensa ¿hasta cuándo se utilizó el signo de negativo para representar a los números negativos? La respuesta la obtendrás en el siguiente video del inicio al minuto 02:00.

• Origen de los números negativos

https://www.youtube.com/watch?v=0pFOxPb458U

Ahora ya sabes lo que son los números naturales y lo que es el conjunto de los números enteros que incorporan a los números negativos.

Ya puedes continuar con los números decimales.

Que al igual que los números naturales, los números enteros y las fracciones, los usas todos los días. Por ejemplo, cuando dices que tu altura es de 1.59 cm o que tu temperatura corporal es de 36.5 grados Centígrados.

En la actualidad parece común utilizar números decimales y representarlos con un punto decimal para separar los enteros de la parte fraccionaria.

Por ejemplo, seis enteros veinticinco centésimos.

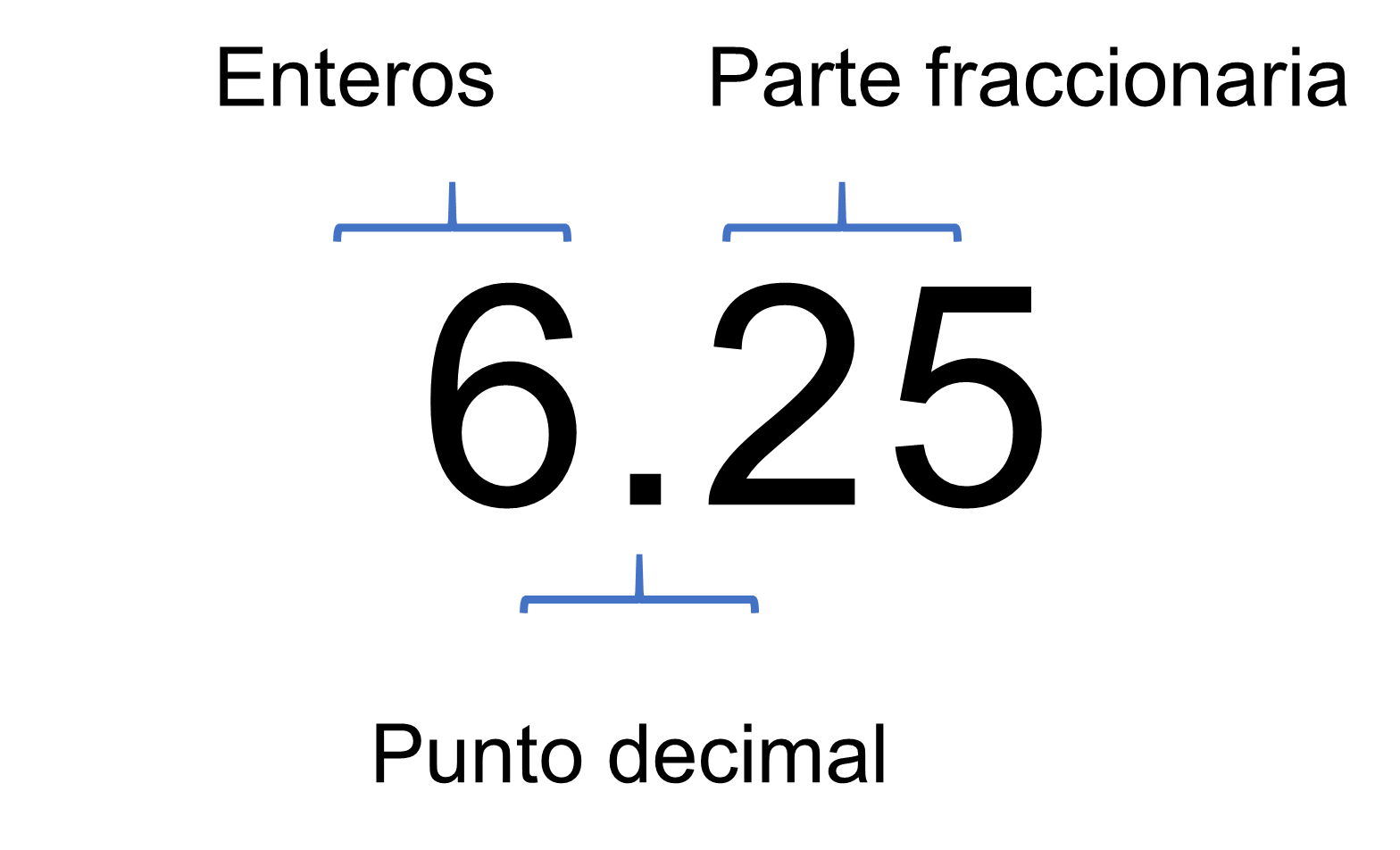
O como tú altura, en metros que se escribe 1 entero con cincuenta y nueve centésimos. Pero no siempre fue así, revisa un poco sobre su historia.

En el siglo diez, un matemático árabe llamado Ya Al Uqlidisi, usaba en sus escritos las fracciones decimales y una notación parecida a la que empleas actualmente, separando la parte entera de la fraccionaria del número mediante una coma.

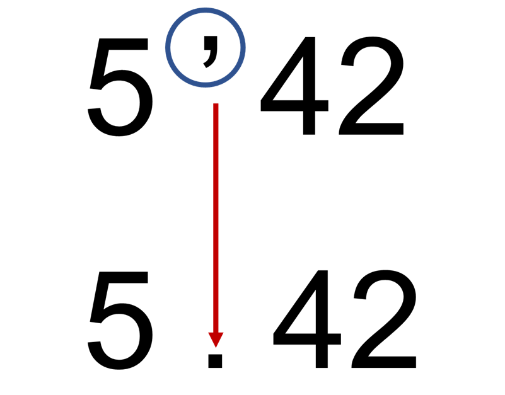
Observa un ejemplo.

Este número se leía cinco unidades y cuarenta y dos de cien.

Lo cual sería equivalente al punto decimal que utilizas.

Ahora, lee dicho número como 5 enteros 42 centésimos.

Al Qasi, otro matemático árabe que vivió a principios del año 1400 introdujo las fracciones decimales a las que llamó décimas, segundos decimales, terceros decimales así creó un sistema para que las operaciones con decimales se efectuaran como se hacía con los números enteros, pero el ingeniero belga Simón Stevin, que vivió en el siglo 16 y principios del 17 dijo:

Stevin, escribió un libro llamado La Dism, que se publicó en 1585 y en el cual propone lo siguiente, “A todo número entero se le llama principio y su signo es, una especie de cero”

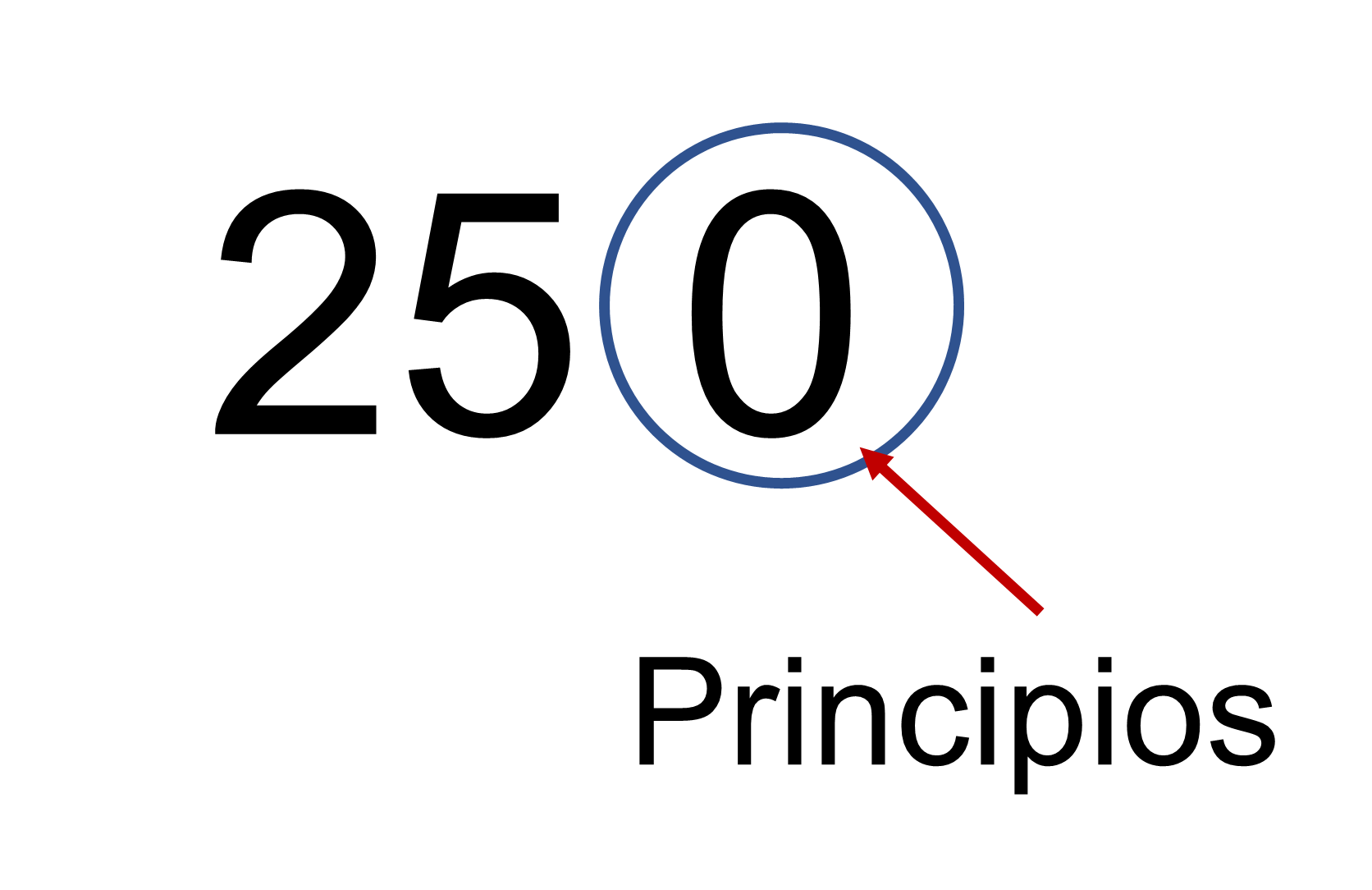
Por ejemplo, este número se lee veinticinco principios. Stevin utilizó este signo para separar la parte entera del número de las fracciones.

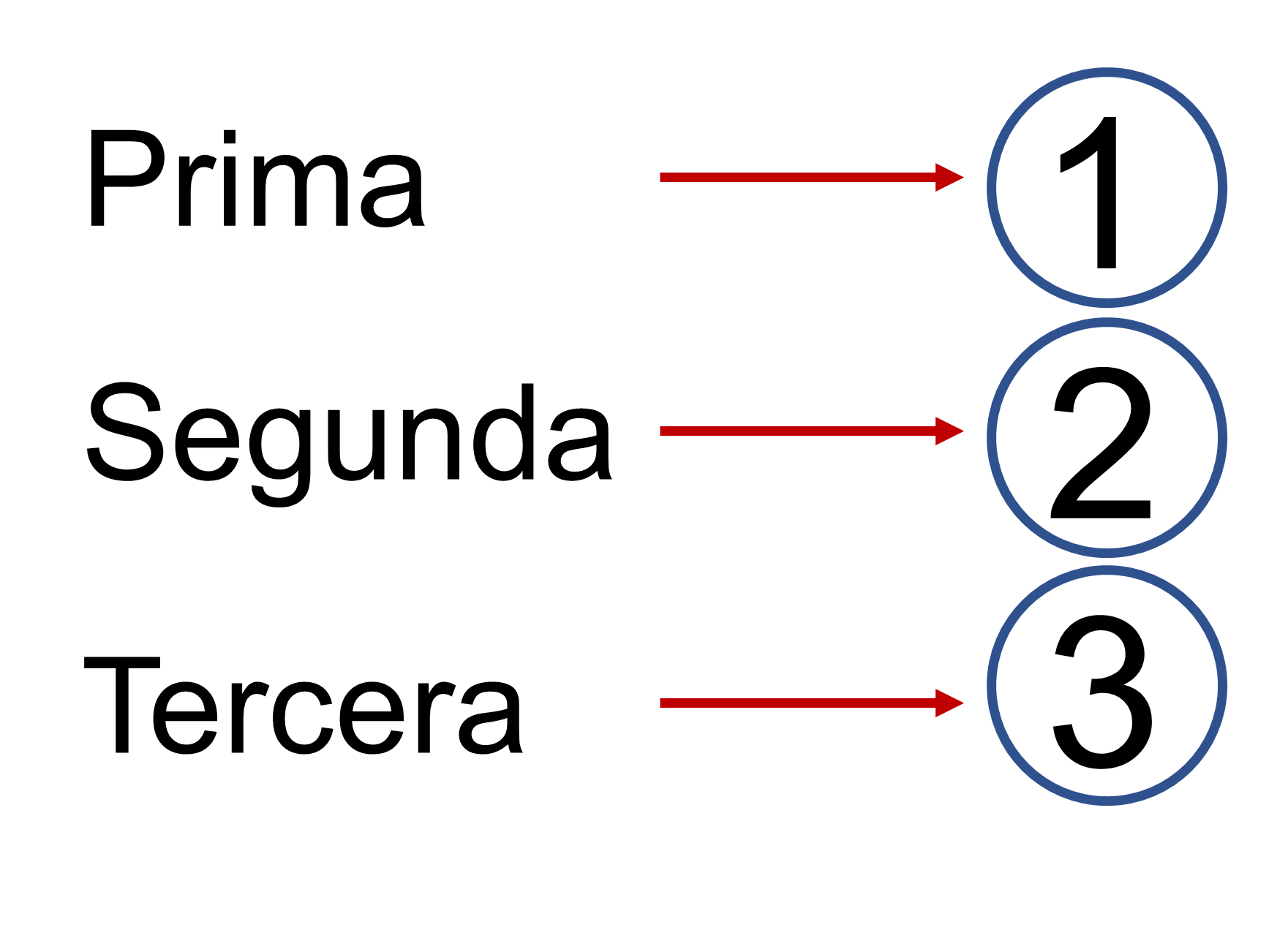
Cada décima parte de la unidad del principio se denomina prima y su signo es uno; la décima parte de una prima se conoce como segunda y su signo es dos; la décima parte de una segunda se llama tercera y su signo es tres, y así sucesivamente.

Este es un ejemplo de ello: tres principios y dos primas ocho segundas y una tercera que equivale a tres enteros dos décimos ocho centésimos y un milésimo. El signo ideado por Stevin se convirtió en el punto decimal que utilizas actualmente. Te imaginas, ¿cuántos signos había que usar para escribir y entender un número decimal?

Son muchos los aportes de las diferentes culturas y de personas en el desarrollo de la forma de representar a los números y sus operaciones.

Todas las culturas han aportado algo de su conocimiento al concepto de número.

Ya conociste una de las propiedades de los números naturales, es decir, revisaste la propiedad de cerradura, pero falta la propiedad de densidad de los números fraccionarios y decimales.

Observa ahora una de las propiedades más importantes de los números fraccionarios y de los números decimales, la propiedad de densidad.

Eso no necesariamente sucede con cualquier número. Lo revisarás a través de algunos ejemplos.

Por ejemplo, piensa algún número natural que esté entre 6 y 7

La respuesta es ninguno, no hay un número natural entre seis y siete.

Ahora revisa un ejemplo con números decimales.

¿Qué decimal está entre 4.3 y 5.3?

La respuesta es:

Siguiente ejemplo: Dos decimales que tengan cifras decimales subsecuentes, por ejemplo.

¿Qué número decimal está entre seis punto cinco y seis punto seis?

Es decir, ¿qué sea más grande que seis punto cinco, pero más chico que seis punto seis?

La respuesta es:

Cualquiera de ellos y muchos más. Así podrías seguir encontrando más números, por eso entre dos números decimales siempre existe otro.

¿Cómo encuentras una fracción que esté entre dos fracciones que tienen el mismo denominador?

Por ejemplo, entre dos quintos y cuatro quintos.

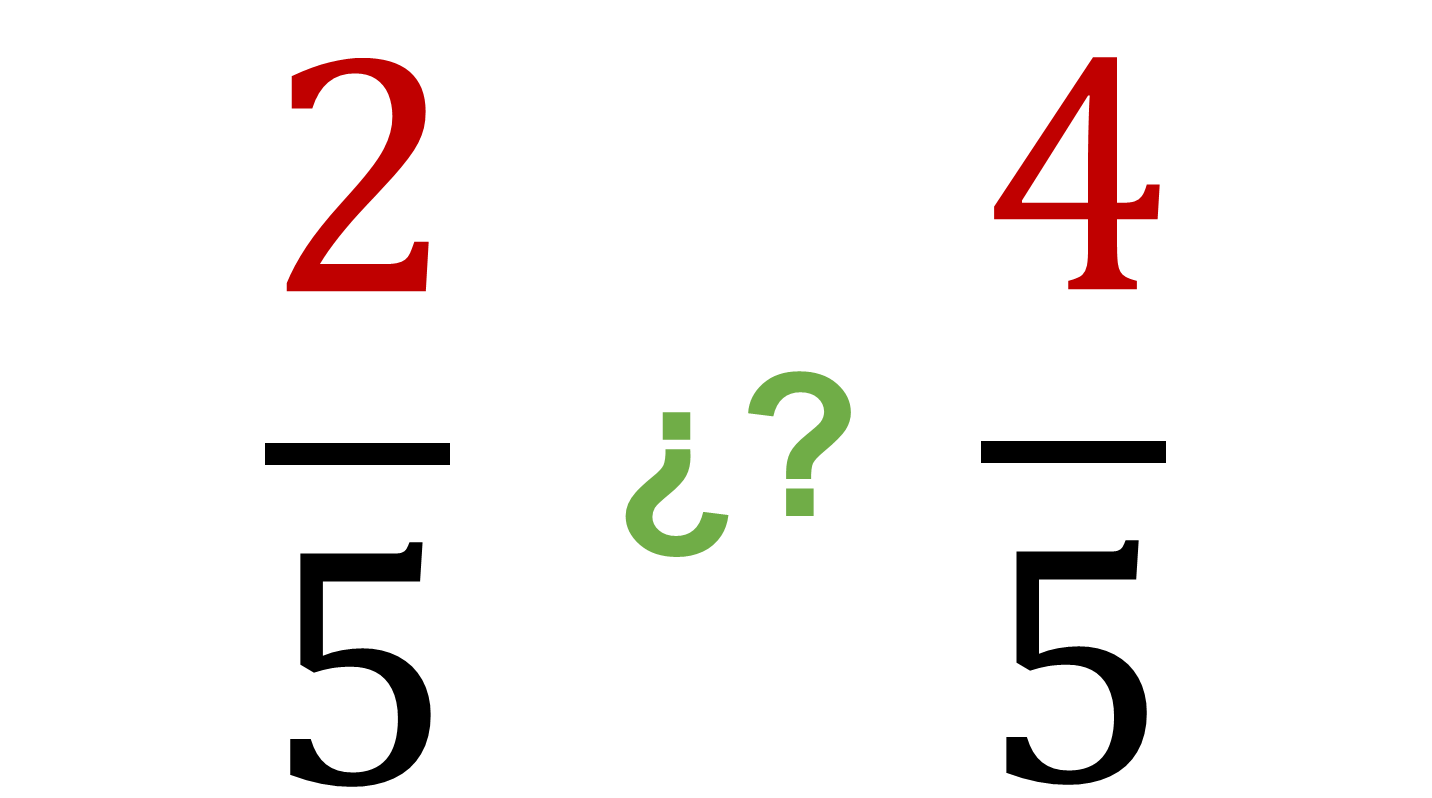
La respuesta es:

Pues tres quintos es mayor que dos quintos y menor que cuatro quintos.

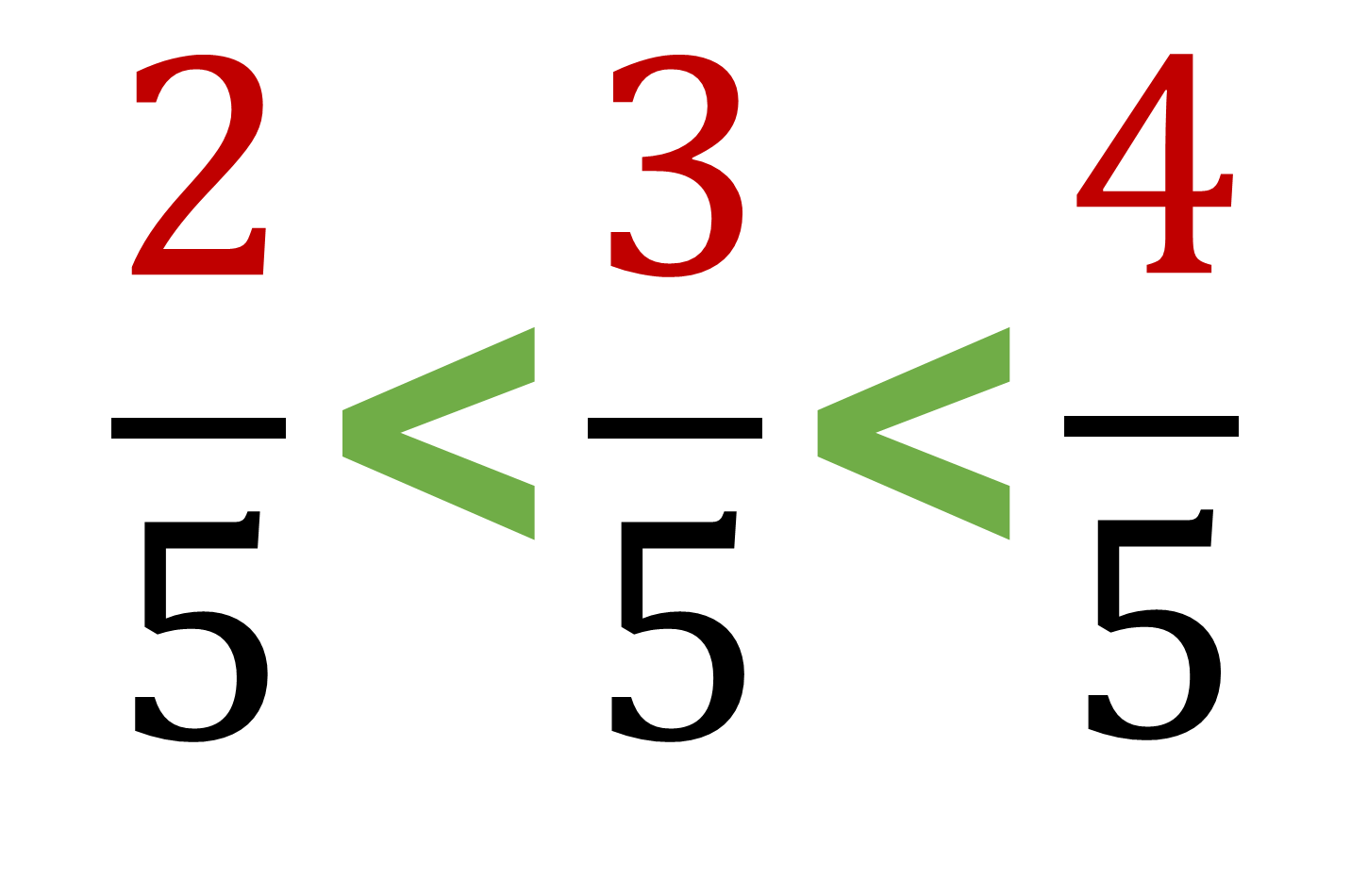
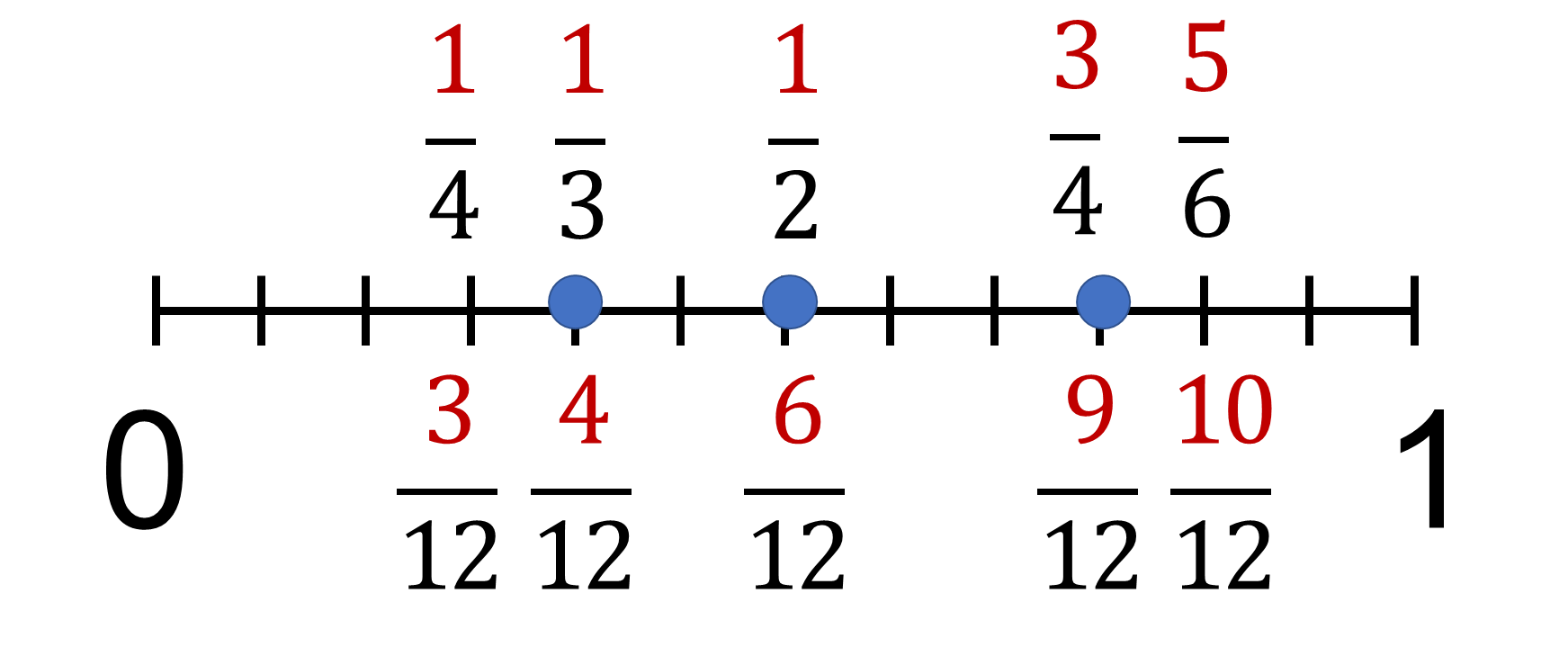
Otro ejemplo; busca una fracción que esté entre un cuarto y cinco sextos, es decir, que sea mayor que un cuarto y menos que cinco sextos.

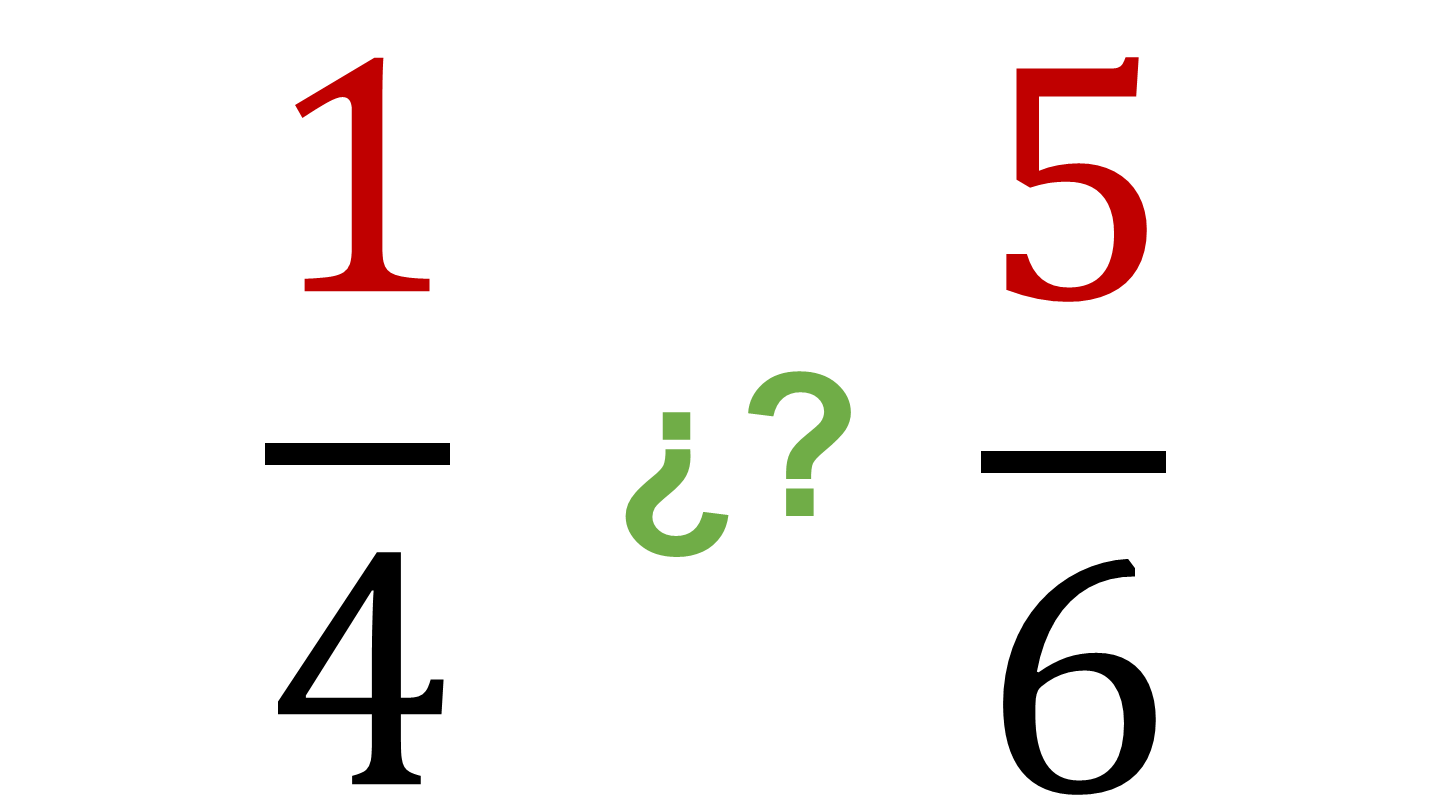
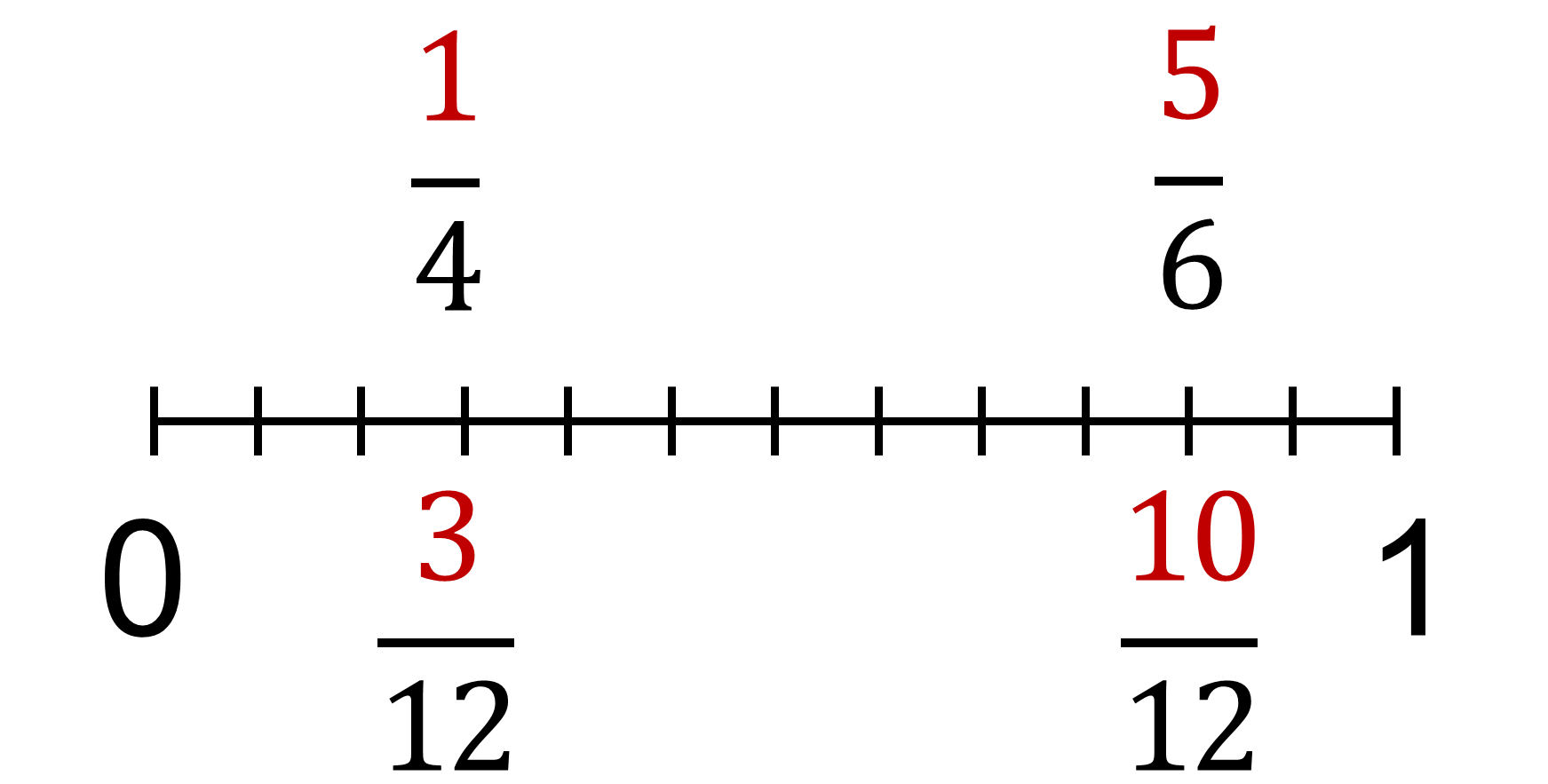
Para encontrar la respuesta puedes trazar una recta numérica para ubicar los dos números como son fracciones propias ambas están entre cero y uno.

Si el común denominador es doce, un cuarto equivale a tres doceavos y cinco sextos equivale a diez doceavos, entonces hay varias fracciones entre ambas.

Por ejemplo, cuatro doceavos es igual a un tercio o nueve doceavos que es igual tres cuartos.

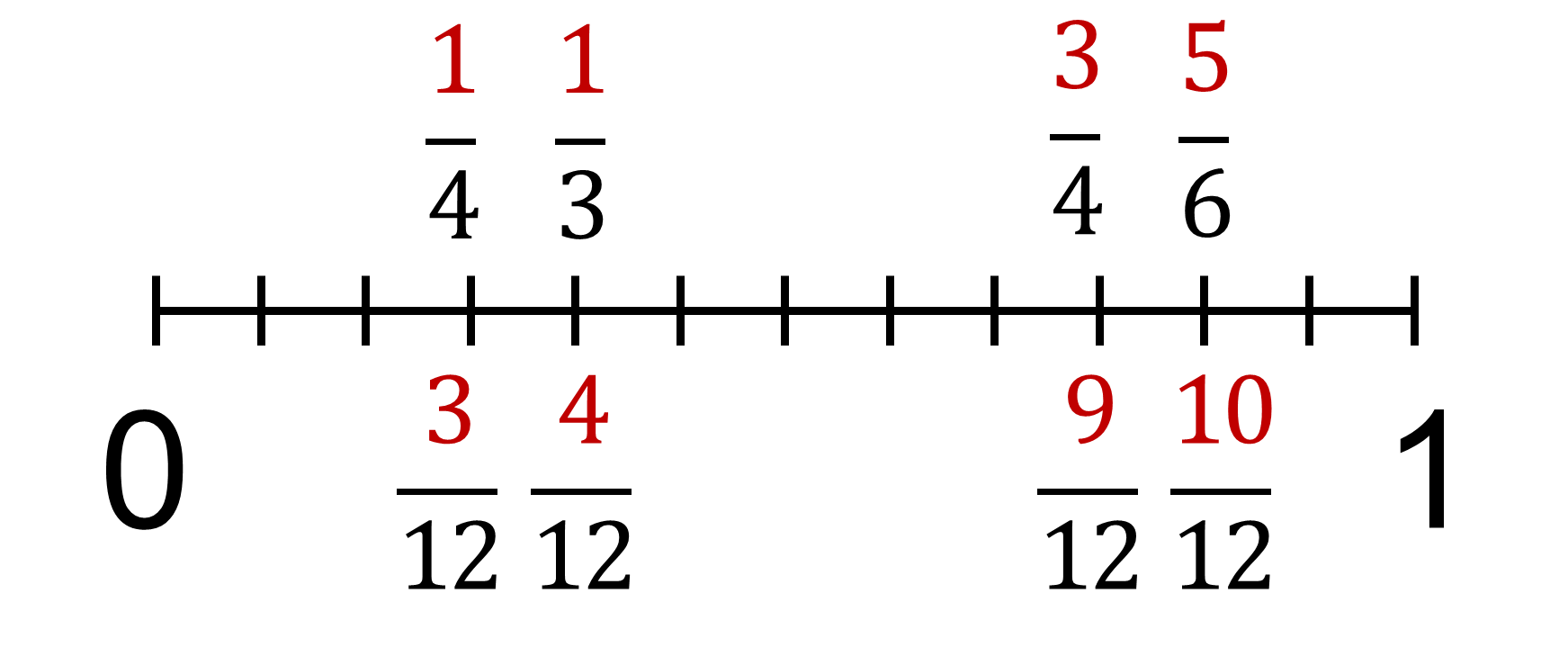
También podrías mencionar seis doceavos que equivale a un medio.

Ahora otra más difícil, encuentra una fracción entre dos quintos y tres quintos.

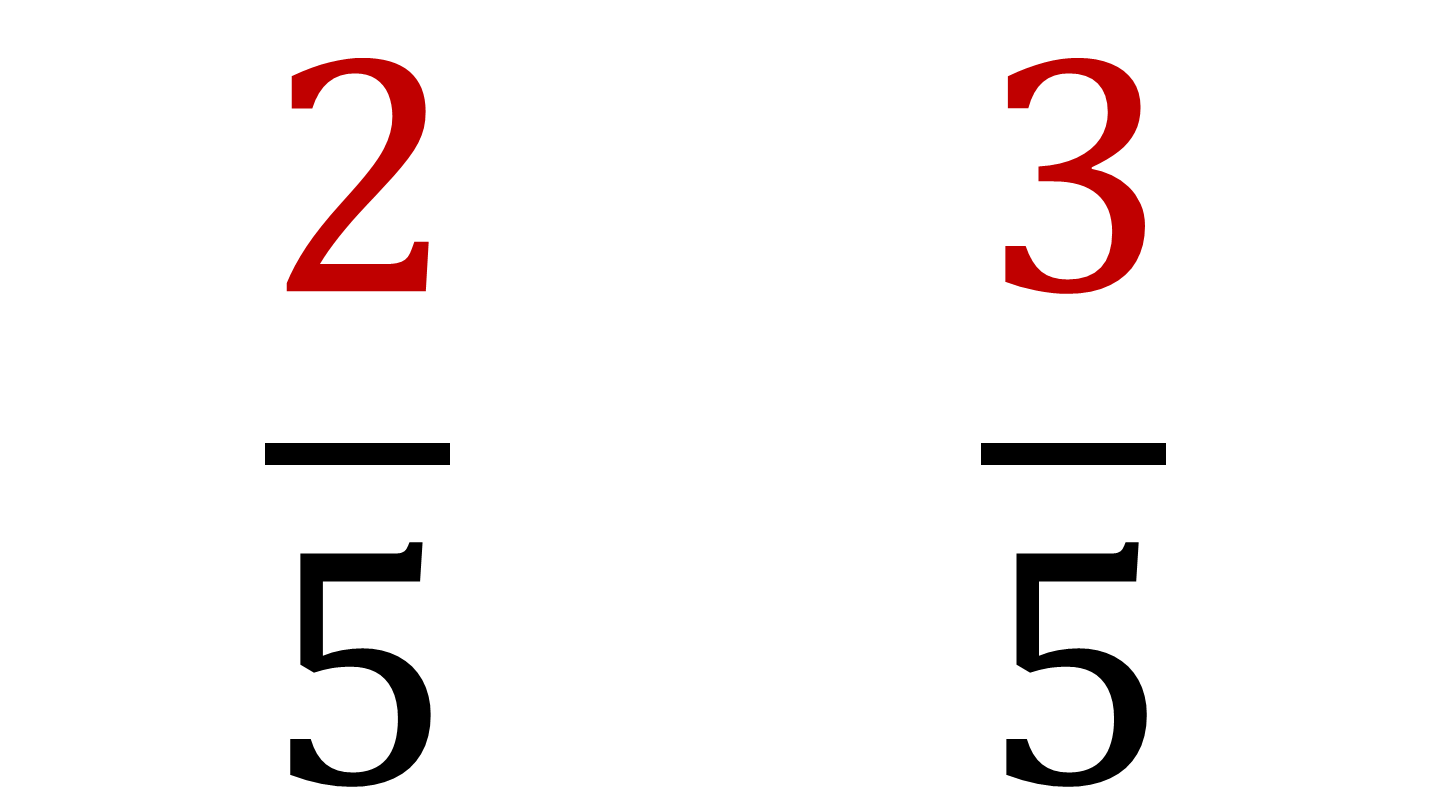
De nuevo trazas una recta numérica y ubica dos quintos y tres quintos, luego la fracción que esté a la mitad, pues esa es la que buscas.

Pero ¿cómo sabes que fracción es?

En este caso, para encontrar la solución hay que buscar otra pareja de fracciones equivalentes a dos quintos y a tres quintos, con un denominador mayor que cinco, por ejemplo, con denominador diez. Entonces, dos quintos es equivalente a cuatro décimos y tres quintos es equivalente a seis décimos.

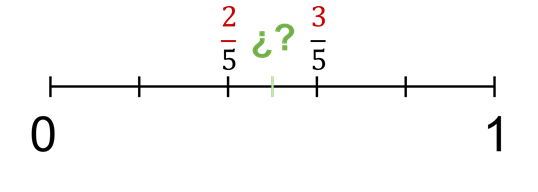
Entonces entre ellas está cinco décimos.

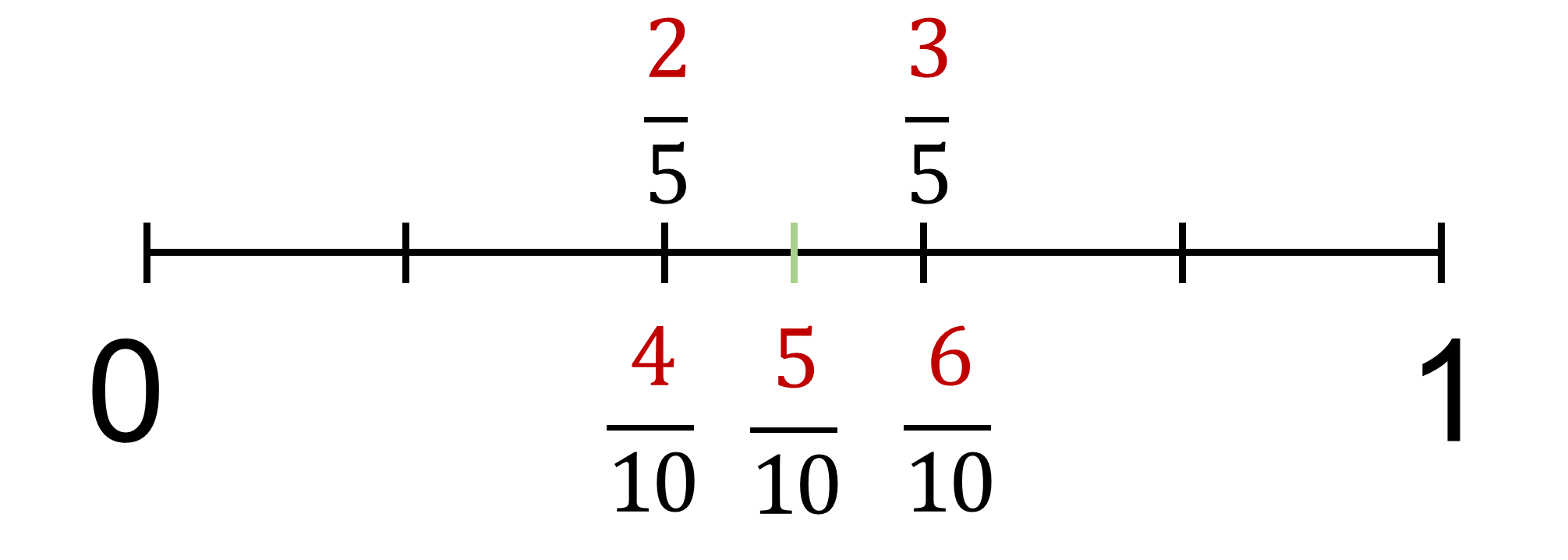
Entre dos fracciones siempre existe otra, o mejor dicho entre dos fracciones hay infinidad de fracciones. Cada vez puedes encontrar algún punto que esté a la mitad de dos fracciones y luego otro que esté de nuevo a la mitad y así sucesivamente.

El reto de hoy:

Incluye fracciones y decimales negativos.

Encuentren un número que esté entre menos seis punto uno y menos trece medios.

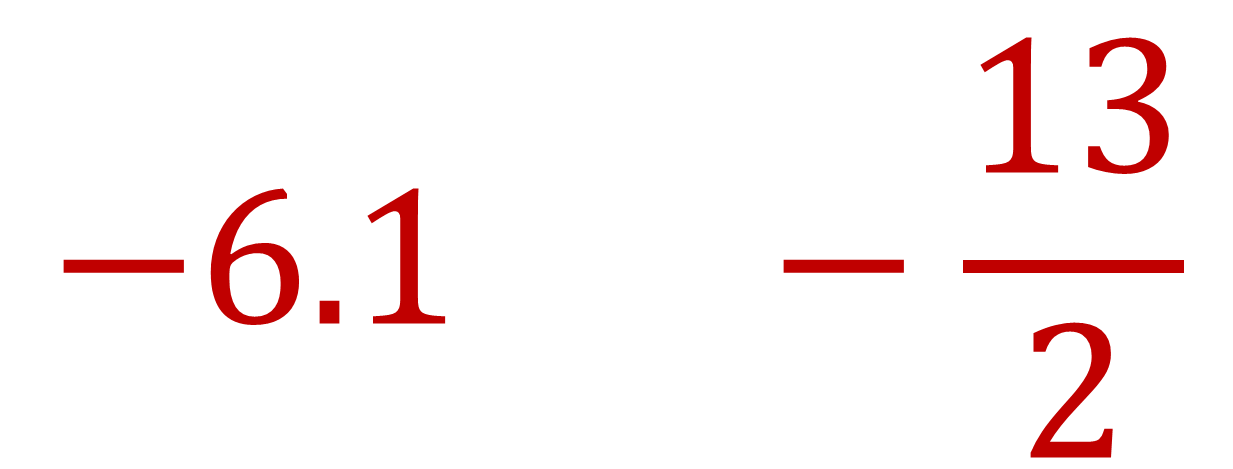
Has revisado cómo las diferentes culturas a lo largo de la historia, en su necesidad diaria de contar, han aportado a la representación de los números y sus operaciones. Así gracias a la representación de los números, las matemáticas proporcionan un lenguaje preciso y conciso para modelar, analizar y comunicar observaciones que se realizan en distintos campos de la vida diaria.

El concepto de número y su notación es la herramienta básica de las matemáticas.

Tu libro de texto de Matemáticas de tercer grado tiene ejercicios similares. Es importante que así practiques lo aprendido.

¡Buen trabajo!

Gracias por tu esfuerzo.

Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.