Multiplico y gano, divido y venzo
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:56Aprendizaje esperado: Resuelve problemas de valor faltante en los que la razón interna o externa es un número natural y, relación del tanto por ciento con la expresión "n de cada 100".
Énfasis: Analiza procedimientos para resolver problemas de proporcionalidad del tipo valor faltante: dobles, triples, valor unitario, suma término a término.
¿Qué vamos a aprender?
Aprenderás a analizar procedimientos para resolver problemas de proporcionalidad del tipo valor faltante: dobles, triples, valor unitario, suma término a término.
¿Qué hacemos?
En la sesión de hoy iremos de regreso en la máquina del tiempo para recordar el tema de proporcionalidad.
Esa región va a ser larga, pues es un tema muy extenso.
Si es amplio el tema de la proporcionalidad, pero no debemos perder de vista algunas cosas.
En primer lugar, todo lo que veamos en esta sesión ya se trató en algún momento, de manera que no será algo que se desconoce.
Y en segundo lugar, este es un viaje para recordar y, por lo tanto, será breve nuestra visita a cada tema. Siempre es interesante y enriquecedor revisar lo que ya sabemos para darnos cuenta de lo que aún nos falta por aprender.
Para empezar, regresemos al ciclo escolar anterior, donde estudiaron y resolvieron algunos problemas de proporcionalidad.

Recuerdas que desde el primer bloque trabajamos la proporcionalidad, con el desafío 17 llamado “Botones y camisas”. Se pedía completar unas tablas y además preguntaban cómo obtuvimos la respuesta.
Efectivamente, se trataba de calcular el valor faltante dado un conjunto de datos que cumplía con una determinada característica.
Te propongo que ejercitemos un poco nuestra memoria y hagamos un ejercicio similar. Observa la siguiente tabla.
¿Cómo podrías saber las cantidades faltantes?
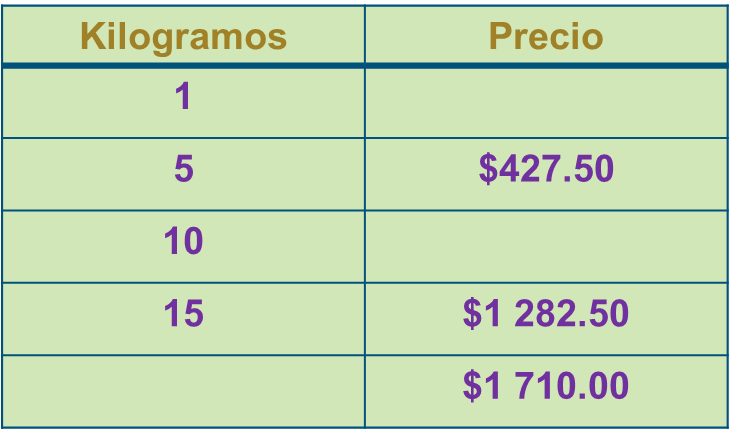
Pues recuerdo que analizamos diversas estrategias. Veamos lo que observo es que son cantidades proporcionales pues si multiplico 5 kilogramos por 3 son 15 y también si multiplico su precio $427.50 por 3 obtengo $1282.50 entonces para saber cuánto cuestan 10 kilogramos, me basta con multiplicar por dos el precio de los 5 kilogramos.
Y para saber las otras dos cantidades faltantes, ¿Qué harías?
Pues si logras saber cuánto cuesta un kilogramo, ya sabrás cuántos kilogramos cuestan 1 710 pesos.

Estás aplicando la estrategia de encontrar el valor unitario y partiendo de ese valor, pues ya es inmediato saber cuánto cuesta cualquier cantidad de kilogramos, o viceversa dada cierta cantidad de dinero, podrás saber mediante el valor unitario, cuántos kilogramos puedes adquirir con ese dinero.
Comienzo a hacer las operaciones, divido 427.50 entre 5 para obtener el valor de un kilogramo; así que eso nos da $85.50. Si un kilogramo cuesta eso, entonces 10 costarán $855.00 por último, saber cuántos kilogramos puedo comprar con $1 710 divido esa cantidad entre 85.50 y el resultado de esa división nos da 20 por lo que puedo comprar 20 kilogramos.
Utilizaste una buena estrategia para obtener los valores faltantes de esa tabla, pero, quisiera proponerte otra posibilidad de conocer la cantidad de kilogramos del último renglón.

Si sumas lo que cuestan 15 kilogramos y 5 kilogramos, te da exactamente 1710 pesos, por lo tanto, habría que sumar 15 + 5 y obtenemos los 20 kilogramos que corresponden a ese precio.
Veamos cómo queda la tabla con los valores que faltaban.

Es verdad, no recordaba que cuando tenemos una tabla de proporcionalidad, podemos analizar la relación entre todas las cantidades para hacer más eficientes nuestros cálculos.
Ves cómo podemos utilizar diferentes estrategias en la resolución de problemas.

Sigamos con nuestro recorrido, en el desafío 55 llamado Un valor intermedio, vimos que cuando varias cantidades están en una relación de proporcionalidad, podemos utilizar una estrategia distinta, por ejemplo, para encontrar los valores faltantes cuando la relación entre las cantidades es de dobles, triples, etcétera.
Analizamos otra forma de encontrar esos valores faltantes, basándonos en que unas cantidades eran múltiplos de otras.

Hagamos un ejercicio de ese tipo para poder recordar esa estrategia, de nueva cuenta, analicemos la siguiente tabla.
Al analizar los datos de la tabla me doy cuenta de que, para obtener el precio de 4 libros, puedo dividir el precio que tenemos de 8 libros entre dos, por lo tanto, cuatro libros cuestan $600 y, además, 12 es igual a 8 + 4 por lo que, para obtener el valor de los doce libros, basta con sumar los dos valores que ya tengo, es decir 1200 + 600 así que los 12 libros cuestan $1 800
Esto se cumple siempre y cuando las cantidades tengan una relación de proporcionalidad. Ve recordado estas útiles estrategias.
Nos disponemos a viajar a otro momento del pasado, ¿Qué visitaremos?
Recordemos cómo se aplicó en la sesión del 25 de marzo esto que acabamos de ver en un problema que nos planteó el alumno Leonardo Ruiz que vive en Guerrero.
- Cuentas claras. Del minuto 03:56 al 09:37
https://www.youtube.com/watch?v=uZdaoZd1NY8
Pudimos ver que se aplicó la misma estrategia de los múltiplos de los números y también nos dimos cuenta que es muy útil tener ordenados los datos en tablas para avanzar sistemáticamente hacia los resultados.
Efectivamente, al analizar la relación que había entre las cantidades, se pudieron encontrar los valores faltantes de una manera más rápida, además, cuando se ordenaron los datos, nos percatamos de esa relación.
Pero ya que estamos con el espíritu de viajar al pasado para recordar las clases que tuvimos sobre la proporcionalidad, viajemos al día 26 de marzo para recordar lo que entendimos como “Ahorro compartido”.
En esa sesión unos estudiantes nos dijeron que resolvieron uno de los problemas planteados de una manera distinta a como hemos estado abordando las situaciones de valor faltante.
Veamos el siguiente video para recordar cómo lo resolvieron ellos.
- La importancia del ahorro. Del minuto 19:40 a 20:30
https://www.youtube.com/watch?v=d5aUZt5uPLE
La estrategia que ellos siguieron es ver qué porcentaje representaban los dólares que enviaban con respecto a los dólares que ganaban.
Sí, y una vez obtenida esa relación, la aplicaron a la cantidad de dólares que les daban como dato, para obtener así cuántos dólares enviaron.
De esa manera estaban haciendo evidente que, si bien las matemáticas requieren práctica, también se necesita comprender el significado de lo que se está haciendo.
Ahora dirijamos visitemos el momento de la clase del 18 de junio en donde seguimos resolviendo problemas de valor faltante.
Esa sesión correspondió al reto 93 “Dinero electrónico”.
No se diga más vamos a viajar hasta ese momento.
- Un detallito. Del minuto 12:30 al 15:50
https://www.youtube.com/watch?v=YifVrW8renY
Al ver cómo calcular el dinero que nos regresan en las tarjetas electrónicas por cada compra que hacemos, podemos armar estrategias y saber cuándo nos conviene hacer o no hacer una compra con esos ganchos publicitarios.
De nueva cuenta se vio otro procedimiento distinto en esa clase que hasta ese momento no habíamos visto.
Estas sesiones de repaso te están ayudando mucho, porque a veces, después de las vacaciones se te olvidan muchos detalles importantes.
Las travesías por sesiones anteriores hacen que retomemos los aprendizajes ya aprendidos, los cuales nos ayudarán a refrescar la memoria y a empezar este nuevo ciclo en mejores condiciones.
Ahora adelantemos un poco nuestro control y vayamos a la clase del 22 de junio.
¿En esa ocasión también vimos problemas de proporcionalidad? Yo recuerdo que la sesión trataba de porcentajes.
Efectivamente, vimos problemas que involucraban porcentajes, pero en cantidades que tenían una relación de proporcionalidad.
Observa el video para recordar esos aprendizajes.
- ¿Cuál me conviene más? Del minuto 06:24 al 08:10
https://www.youtube.com/watch?v=OyrDY1iJQ1M
En esa ocasión comparamos el descuento que ofrecían dos tiendas por productos similares.
Con ayuda de nuestros conocimientos sobre proporcionalidad pudimos determinar qué tienda vendía más barato.
En esta ocasión, estos aprendizajes matemáticos sí tuvieron una utilidad inmediata en mi familia, pues pudimos saber si en verdad los descuentos que nos ofrecían algunas tiendas en las compras que íbamos a hacer nos convenían y también pudimos determinar cuál descuento era mejor.
Nuestro combustible ya está a punto de agotarse y sólo nos queda lo suficiente para visitar una última clase en este recorrido temporal.
Así que vayamos directo a la clase del 23 de junio y recordemos lo que estudiamos en esa ocasión.
El tiempo no perdona y ya casi se nos agota, de modo que viajemos al pasado hasta llegar al 23 de junio.
- Las alfombras. Del minuto 06:45 al 09:08
https://www.youtube.com/watch?v=A2ZmVQFnx9c
En esa sesión vimos lo que significa que descuenten cierta cantidad, de acuerdo con el monto de la compra.
Una vez más, vistes la utilidad de aprender el concepto de proporcionalidad para facilitarnos los cálculos.
Ya con esta última parada, tendremos que dar por concluido nuestro recorrido.
Pues entonces regresemos a nuestra base teniendo la seguridad de que con lo que hemos visto en todos estos viajes nos ayudará a comenzar un nuevo ciclo con la mejor preparación.
Esperemos que con este recorrido al pasado por la región de la proporcionalidad haya sido útil para tener muy frescos estos temas y algunas estrategias de solución.
Estos viajes por el tiempo son alucinantes y me traen a la memoria no sólo los aprendizajes matemáticos, sino todo lo que ha significado el tomar clases de una forma inédita.
Lo que vivimos el año de 2020 ha sido único en la historia de la humanidad, para bien y para mal, además nos permitió explorar formas inéditas de aprendizaje y de convivencia.
Si te es posible consulta otros libros y comenta el tema de hoy con tu familia.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.



Login to join the discussion