Muestreo

Muestreo

Aprendizaje esperado: calcula y explica el significado del rango y la desviación media.

Énfasis: estudiar muestras.

¿Qué vamos a aprender?

En esta sesión, trabajarás el diseño y obtención de información de una encuesta de una población en estudio.

Los materiales que vas a utilizar en esta sesión será cuaderno de apuntes, lápiz y goma. Al final de la sesión o cuando lo consideres necesario podrás consultar tu libro de texto.

Ya sabes cómo aplicar encuestas a una población de estudio para obtener información, y cómo analizar esta información con el uso de las medidas de tendencia central, como son la media, mediana y moda.

Ahora, en esta sesión profundizarás con el análisis, pero no de una población, que es un conjunto de elementos que han sido escogidos para su estudio, sino que se escogerá un segmento con una característica o atributo en común observable, a la cual identificarás como población en estudio.

¿Qué hacemos?

La mayoría de las veces, al realizar una investigación, no se cuenta con el tiempo, los recursos o los medios para la obtención de datos, y esto no permite estudiar una población completa. En estos casos, seleccionarás una muestra de la población de estudio.

El muestreo es una técnica estadística en la que se revisa un subconjunto de una población de estudio y tiene, como principal propiedad, que es representativo del total, o sea, de la población considerada.

El muestreo es el procedimiento que se emplea para extraer una pequeña parte de una población de estudio dentro de un universo o población, a ésta se le llama espacio muestral.

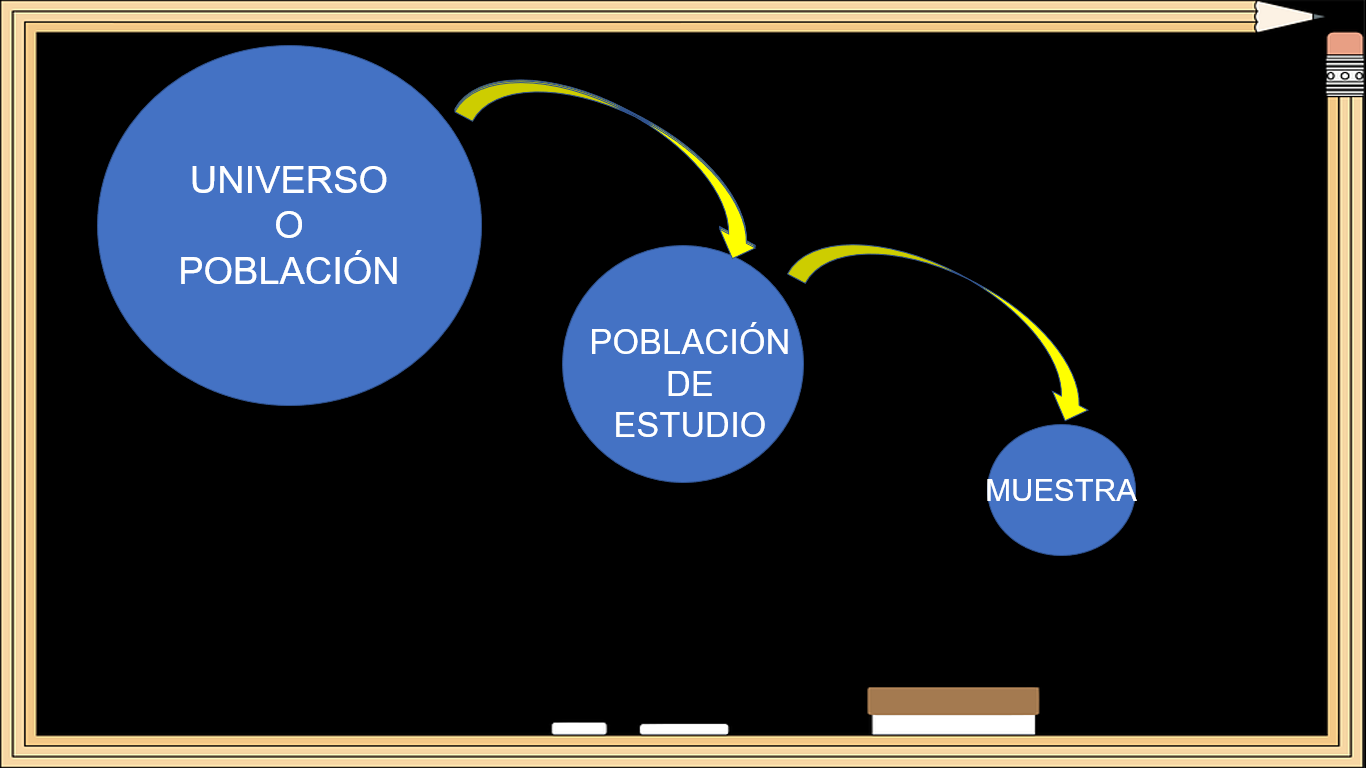
La muestra debe lograr una representación adecuada del universo, en la que se reproduzcan de la mejor manera los rasgos esenciales del mismo y que son importantes para el trabajo. Para que una muestra sea representativa, y por lo tanto útil, debe reflejar las similitudes y diferencias encontradas en el universo o población, es decir, ejemplificar las características de éste. Observa un ejemplo para que quede más claro.

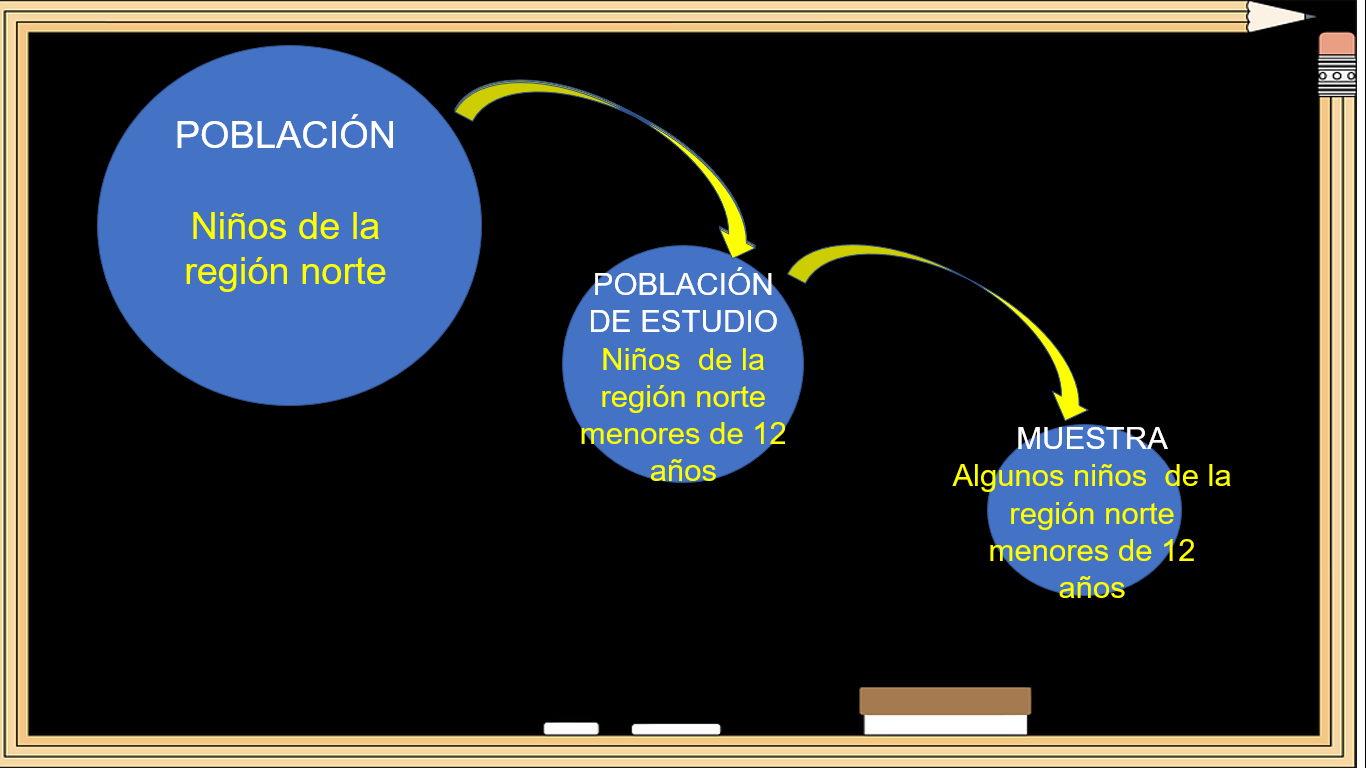
Deseas analizar en qué proporción los niños menores de 12 años de la región norte toman “Dulcileche” en el desayuno.

La población son los niños de la región norte, la población en estudio son los niños de la región norte menores de 12 años, y la muestra serán algunos niños de la región norte menores de 12 años, a los que se les preguntará si consumen “Dulcileche” en el desayuno.

Para aplicar un muestreo puedes utilizar enfoques de muestreo estadístico. El muestreo requiere el uso de técnicas que permitan la formulación de conclusiones sobre una población con una base matemática.

Considera las siguientes preguntas:

• ¿Qué características debe tener una muestra?
• ¿Cuáles son los métodos o técnicas de muestreo?
• ¿Cuál debe ser el tamaño de la muestra?
• ¿Dónde se puede aplicar el muestreo?

Inicia con las características con las que debe contar una muestra para que ésta sea confiable

• Se debe considerar el objetivo específico que se ha de lograr.
• La combinación de procedimientos que tienen mayor posibilidad de alcanzar dicho objetivo, es decir, el método o la técnica a utilizar.
• La relevancia y fiabilidad de la información que se utilizará.
• La elección de un tamaño adecuado de la muestra con precisión, es decir, el margen de error, y un nivel de confianza aceptable.

Ahora, inicia con el análisis de los métodos o técnicas de muestreo que te permitan obtener información fiable de la población; existen varios métodos, analizarás algunos de ellos.

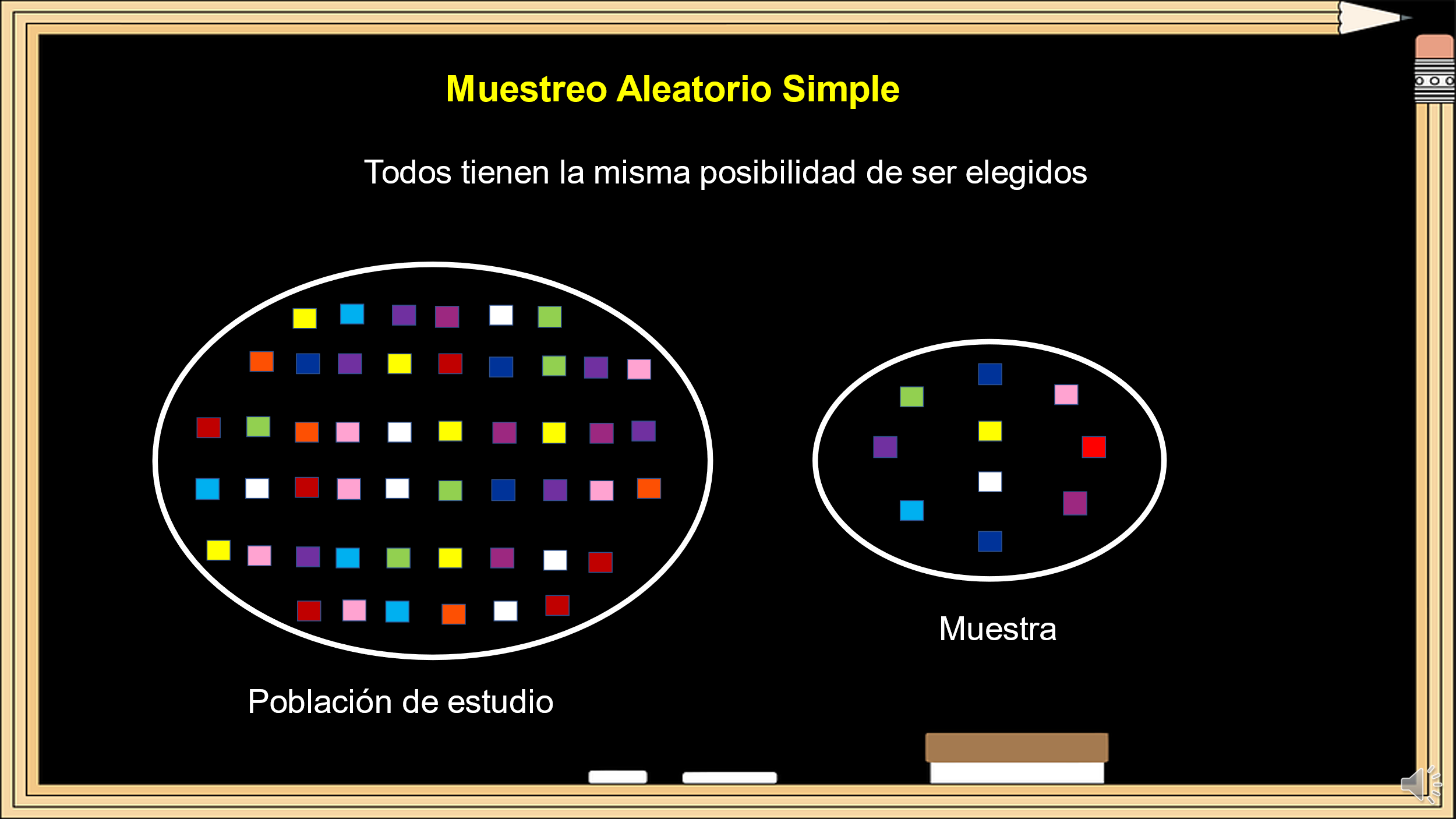
El primero es el Muestreo Aleatorio Simple. Cada elemento de la población tiene la misma posibilidad de ser elegido al azar.

Supón que tienes una población de 50 elementos y quieres estudiar una muestra de 10 elementos que se eligen al azar. Todos tienen la misma posibilidad de ser seleccionados.

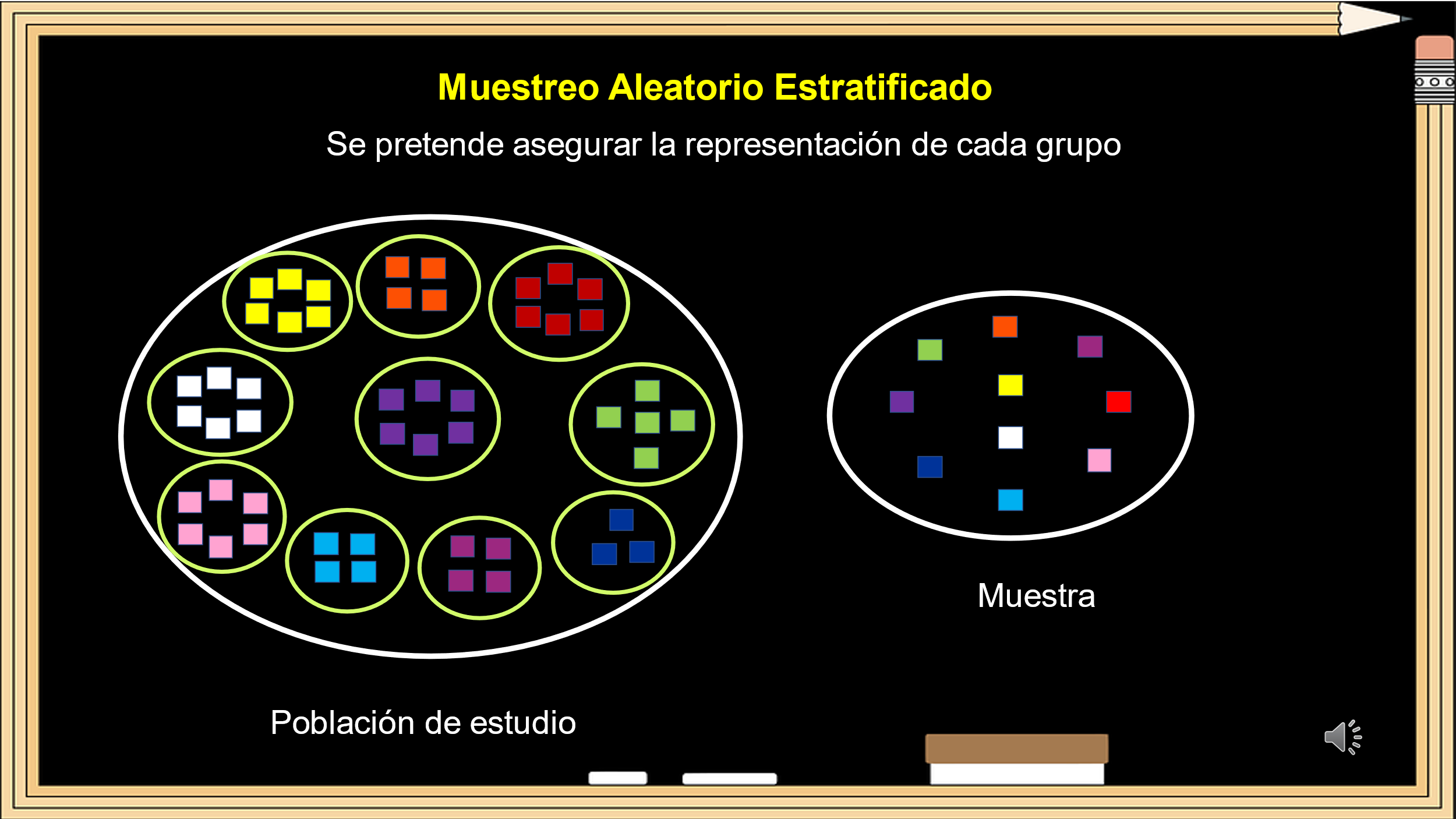
El segundo es el Muestreo Aleatorio Estratificado, cuando se tienen varios grupos o estratos separados y se desea asegurar que todos los estratos están correctamente clasificados, se pretende asegurar la representación de cada grupo en la muestra

La misma población de 50 elementos se encuentra separada por grupos homogéneos, de los cuales se toma un representante de cada estrato para formar la muestra.

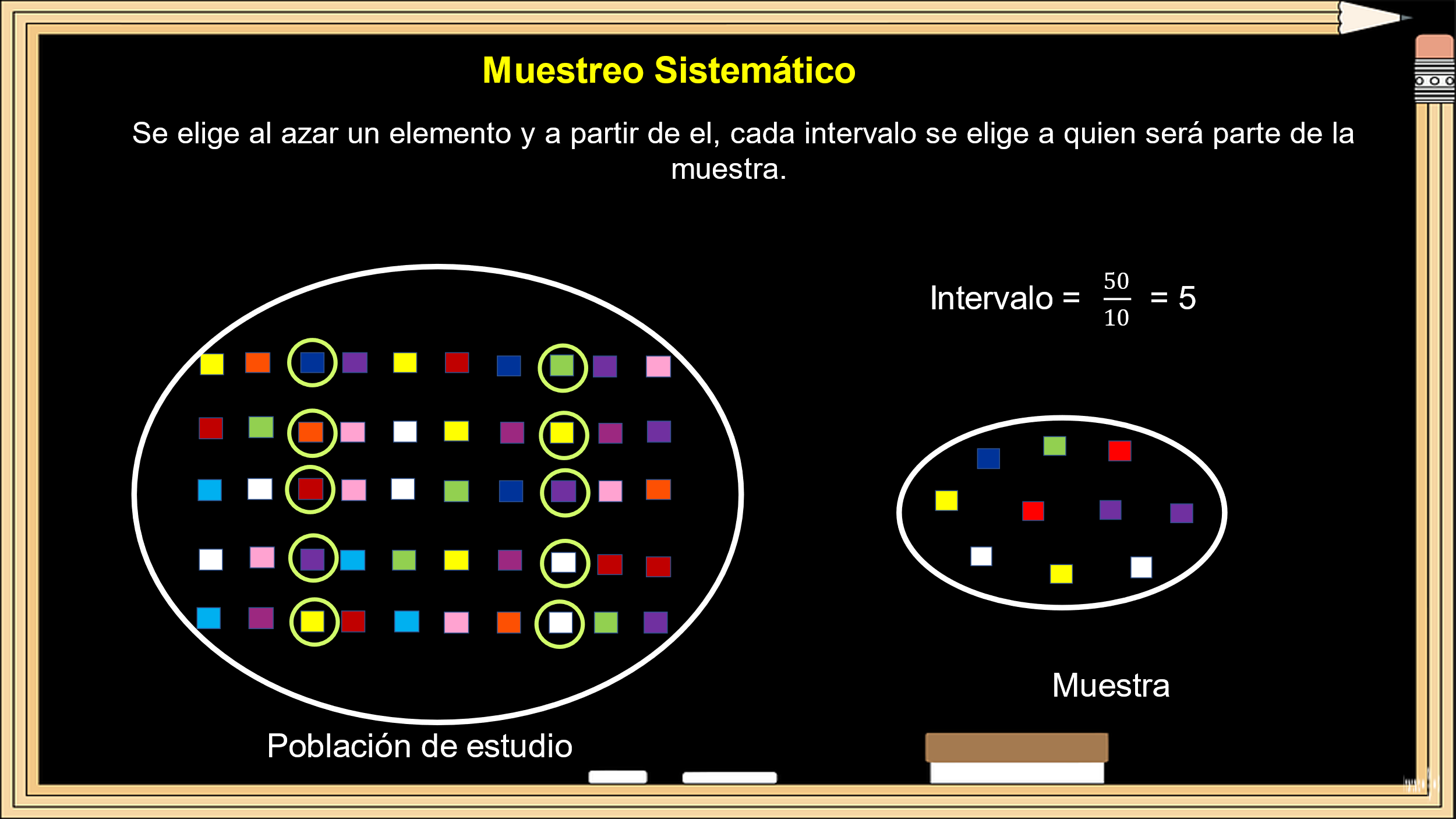
El tercero es el Muestreo Sistemático, aquel donde primero se listan todos los elementos de la población, y después se elige uno de ellos de manera aleatoria y se van escogiendo los siguientes, considerando un intervalo sistemático. Para elegir el intervalo, se divide el total de la población de estudio entre el número de elementos que tiene la muestra.

Se calcula el intervalo, dividiendo 50 de la población entre 10, que es el número de elementos de la muestra, obteniendo 5; posteriormente, se elige al azar un elemento y a partir de él se cuenta cada 5 elementos quién será parte de la muestra.

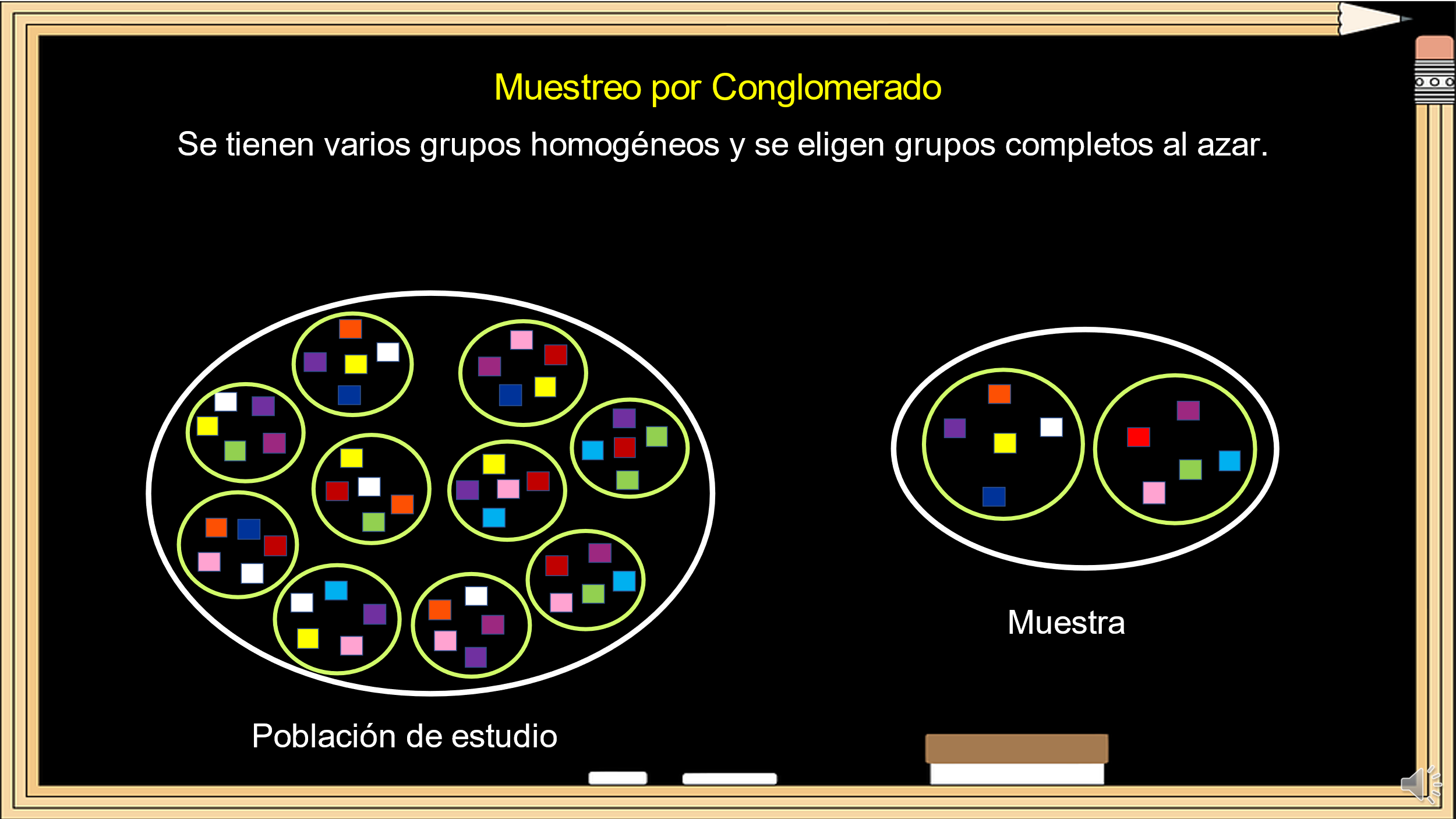
El cuarto es el Muestreo por Conglomerados, cuando los elementos que van a formar parte de la muestra son una colección o conglomerado de unidades de análisis o elementos.

La población de estudio se encuentra conglomerada en grupos, suponiendo que no hay mucha variación entre ellos y se eligen al azar grupos completos, quienes serán parte de la muestra.

Anota en tu cuaderno tus reflexiones, así como posibles dudas, para disiparlas a lo largo de la sesión.

Analiza la siguiente pregunta, ¿qué tamaño de muestra necesitas usar para estudiar cierta población?

El tamaño de una muestra depende del tamaño de la población de estudio y del nivel de error que se esté dispuesto a aceptar. Cuanta más precisión exija, mayor debe ser la muestra que se necesita. Si se quiere tener una certeza absoluta en tu resultado, la muestra tendrá que ser tan grande como la población de estudio.

También es importante considerar que el tamaño de la muestra tiene una propiedad fundamental que explica por qué el muestreo se usa tanto. Esta propiedad podría resumirse como sigue a medida que se estudian poblaciones mayores, el tamaño de muestra que necesitas, cada vez representa un porcentaje menor de dicha población.

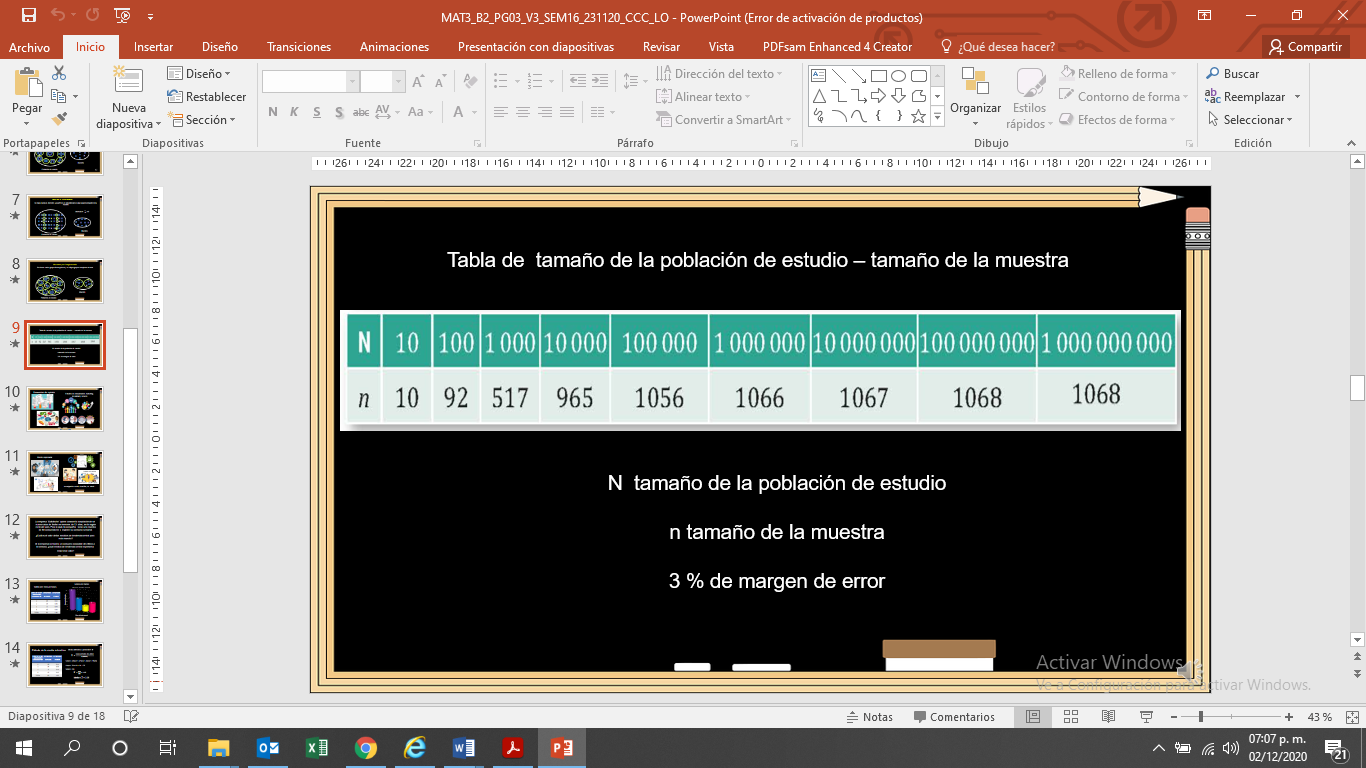
Para que tengas una mejor idea de esta propiedad, observa la siguiente tabla obtenida de un libro de texto de secundaria de tercer grado.

Te muestra a “N” mayúscula, como el tamaño de la población de estudio, y “n” minúscula el tamaño de la muestra con un margen de error de 3%. En la tabla se observa que, conforme crece la población, el tamaño de la muestra crece en menor proporción cada vez.

Para finalizar con el cálculo del tamaño de una muestra, debes tomar en cuenta que se requiere conocer ciertos datos, como son: el nivel de confianza, precisión o error y algunas características de la población.

Ahora, observa la aplicación del muestreo, que es muy amplia, ya que se puede emplear en:

Encuestas de opinión de una población general, sobre temas comunes que suelen afectar a todos los miembros de una misma comunidad, como la economía, salud, política, entre otras.

Estudios de medios de comunicación con respecto a su preferencia, estudios de mercado y marketing para conocer el comportamiento del consumidor, bien o servicio, en estudios de calidad y satisfacción del servicio.

El muestreo es utilizado en la industria, no sólo de forma externa hacia sus clientes o consumidores, también es posible en:

El análisis del diseño empresarial y organizacional para mejorar las estructuras organizacionales

En la investigación social aplicada, tanto a nivel de Ciencias Sociales como de Ciencias de la Salud, Humanidades, entre otras.

El muestreo es un tema muy útil y con una gran aplicación.

Ahora retoma el problema inicial de la sesión, el cual dice:

Sabes que la población de estudio es toda la región norte del país, del cual se nos proporciona una muestra de 80 menores.

La empresa no enlista los resultados, los presenta en forma de:

Tabla de frecuencias con cuatro opciones, con sus respectivas frecuencias, absoluta y relativa, y gráfica de barras.

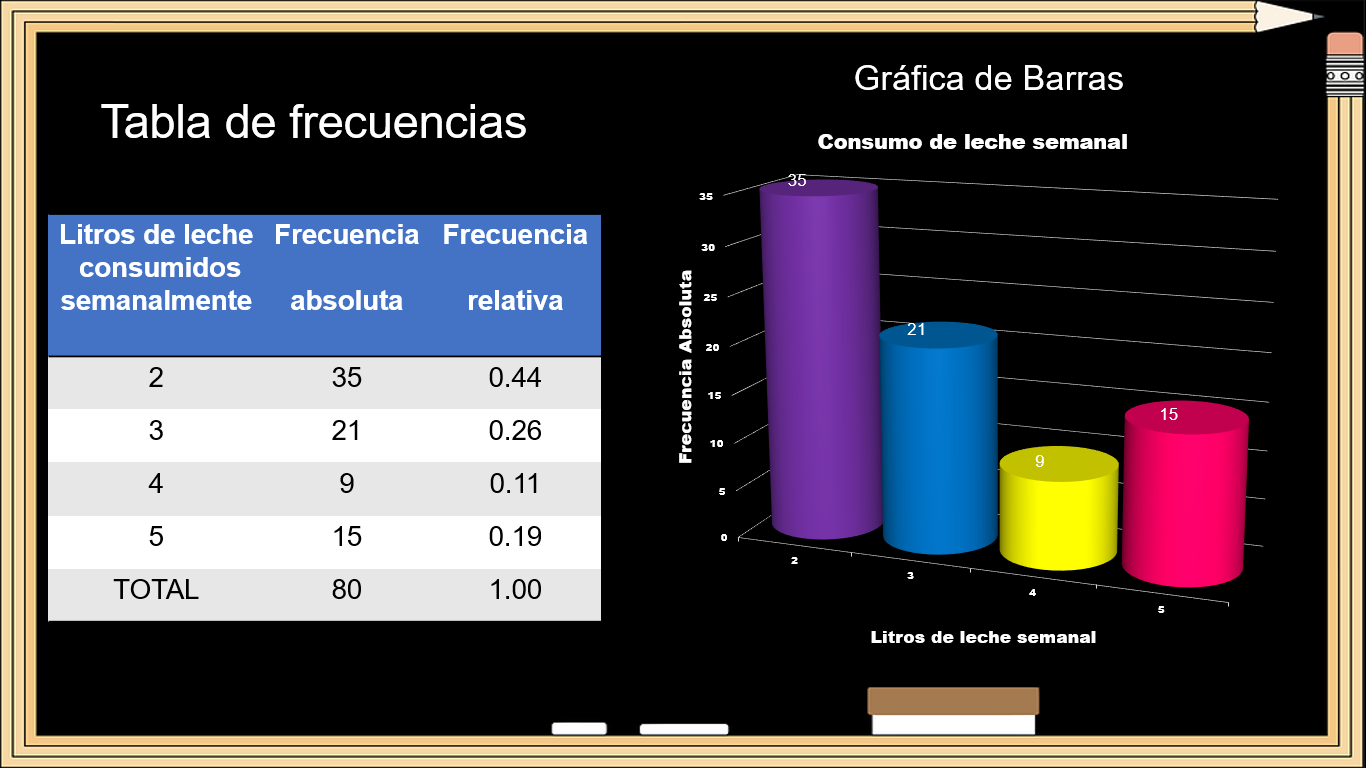
Con la información proporcionada inicia con el cálculo de las medidas de tendencia central.

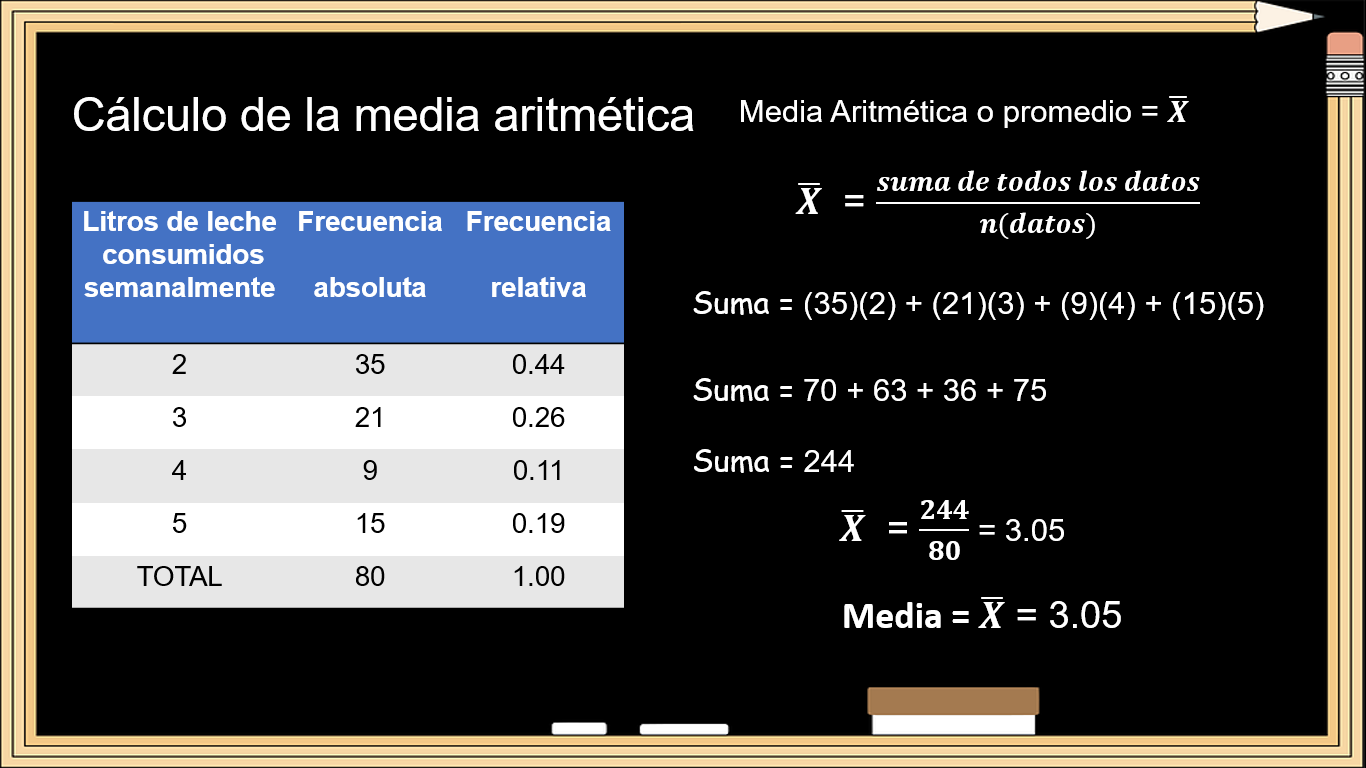
El primer cálculo es la media aritmética, también conocido como promedio. Ya sabes que, para calcular la media aritmética, sólo se deben sumar todos los datos de la muestra entre el total de datos.

Estos son los datos proporcionados en la tabla, no cuentas con los 80 valores de forma individual, pero a través de la frecuencia absoluta multiplicada por cada litro consumido semanalmente, te permite calcular la sumatoria de los datos, es decir, la sumatoria es igual a 35 por 2, más 21 por 3, más 9 por 4, más 15 por 5, igual a la suma de 70 + 63 + 36 + 75, igual a 244. La media aritmética es igual a 244 entre 80, igual a 3.05.

La media aritmética de la muestra es igual a 3.05.

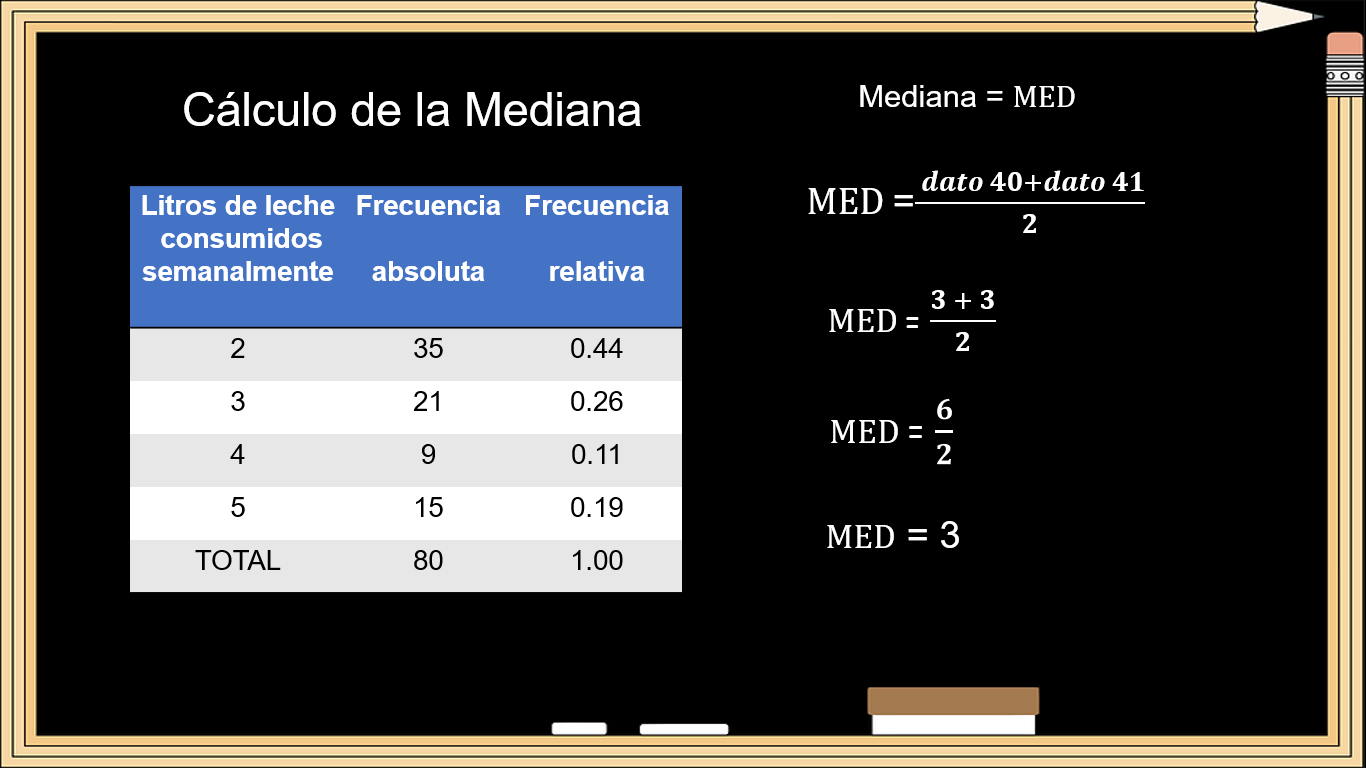
Ahora obtén la mediana del conjunto de datos; para ello necesitas los datos ordenados de forma ascendente o descendente, para considerar el dato que se encuentra a la mitad.

Al estar presentes los datos en forma de tabla, sólo debes ubicar en la frecuencia absoluta, donde se encuentra la mitad.

Si tienes 80 datos, y buscas el que se encuentra a la mitad, son el dato 40 y 41, de los cuales vas a obtener su promedio, es decir, si tienes 35 datos que consumen 2 litros de leche semanalmente, el dato 40 y 41 se localizan en el consumo de 3 litros, ya que son 21 valores en ese dato.

Se suman 3 más 3 entre dos, igual a 6, entre dos, igual a 3.

La mediana de la muestra de datos es igual a 3.

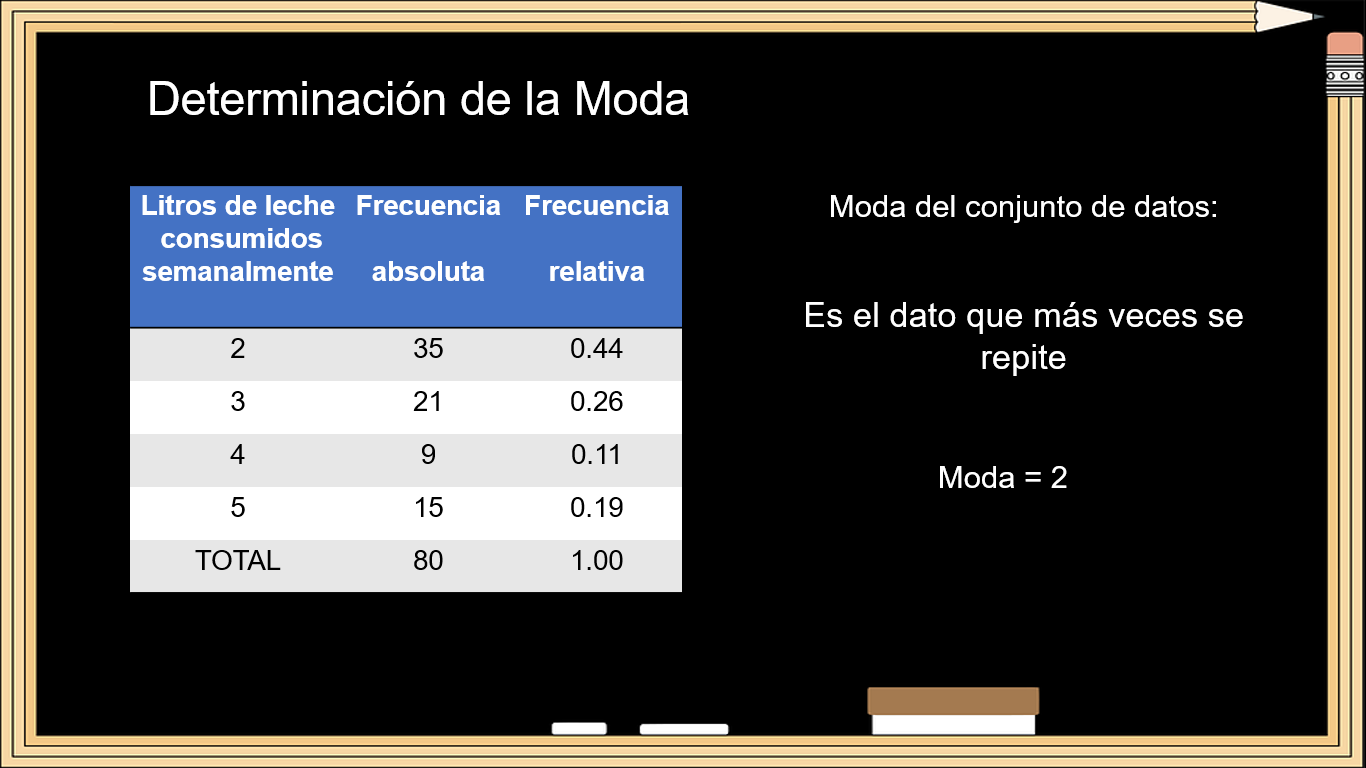
Sólo hace falta calcular la moda de este conjunto de datos. Como ya saben, la moda es el dato que más se repite

Los datos de la tabla permiten ubicar de una forma muy rápida cuál es el valor que más veces se repite, que es el número 2.

Por lo tanto, la moda de la muestra es 2.

Con los cálculos de las medidas de tendencia central, ahora puedes contestar las preguntas de inicio.

¿Cuál es el valor de las medidas de tendencia central para esta muestra?

Para una muestra de 80 menores de 12 años de la región norte del país que consumen “Dulcileche”, las medidas de tendencia central son:

Para finalizar con el ejemplo, si la empresa considera un consumo aceptable de 3 litros a la semana, ¿cuál medida de tendencia central representa mejor este valor?

Observa que, tanto la media aritmética, como la mediana, prácticamente tienen el mismo valor, por lo tanto, la muestra cumple con el consumo esperado de la empresa.

Interesante problema, las medidas de tendencia central calculadas en una muestra tienen una gran aplicación, no sólo en el estudio de mercado, como ya lo analizaste con anterioridad.

Ya sabes que cuando la población de estudio es pequeña, no justifica el tener que tomar una muestra, pero si se va a extraer, debes tener cuidado para que ésta sea confiable.

La muestra debe considerar el objetivo a lograr, que la información sea confiable, los métodos y técnicas de muestreo sea el más adecuado, así como un tamaño de muestra representativo.

No olvides, cuando se generalizan los resultados, es posible cometer errores.

Los errores más comunes que se pueden cometer al estudiar una muestra son:

1.- Hacer conclusiones muy generales a partir de la observación de sólo una parte de la población. A esto se le denomina error de muestreo.

2.- Hacer conclusiones hacia una población mucho más grandes de la que originalmente se tomó la muestra. Se conoce como error de inferencia.

Por último, para reflexionar, como decía el escritor británico H. G. Wells: “El pensamiento estadístico será algún día tan necesario para el ciudadano competente, como la habilidad de leer y escribir”.

El reto de hoy:

Busca en tu libro de texto todo lo relacionado con este tema, y resuelve los ejercicios que ahí se proponen. Así, podrás enriquecer tu conocimiento y tomar notas en tu cuaderno.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/secundaria.html