Método de suma y resta

Aprendizaje esperado: resuelve problemas mediante la formulación y solución algebraica de sistemas de dos ecuaciones lineales con dos incógnitas.

Énfasis: resolver problemas mediante el planteamiento y la solución de sistemas de dos ecuaciones lineales con dos incógnitas utilizando el método de suma y resta.

¿Qué vamos a aprender?

Se te recomienda participar activamente, anotar las ideas principales del tema y las dudas que surjan.

En esta sesión, resolverás problemas que se pueden modelar con sistemas de dos ecuaciones lineales con dos incógnitas. En la resolución de esos sistemas se usará el método de suma y resta.

¿Qué hacemos?

Para comenzar, lee detenidamente el siguiente ejercicio:

La suma de dos números es 30 y su diferencia es 6. ¿Cuáles son los números?

Una vez leído el problema, estima qué números cumplen con las condiciones descritas y anota la estimación en tu cuaderno.

A continuación, se resolverá el ejercicio con base en un sistema de dos ecuaciones lineales con dos incógnitas.

Para eso, primero plantea dicho sistema. Puedes utilizar como guía las siguientes preguntas o consideraciones:

1. ¿Cuáles son las cantidades desconocidas o incógnitas del ejercicio?

2. Asigna una letra o literal distinta a cada una de las incógnitas.

3. Con base en lo anterior, ¿cómo se puede representar algebraicamente el enunciado “la suma de dos números es 30”? ¿Y el enunciado “y su diferencia es 6”?

En la primera pregunta se solicita identificar las incógnitas del ejercicio. Léelo nuevamente:

“La suma de dos números es 30 y su diferencia es 6. ¿Cuáles son los números?”. Se pueden identificar como incógnitas dos números.

En la segunda pregunta, se solicita asignar letras a las cantidades desconocidas identificadas. Aquí, se asignará la letra “x” a uno de los números y la letra “y” al otro número.

En la tercera pregunta, se solicita representar algebraicamente el ejercicio. El enunciado “La suma de dos números es 30”, se puede representar con la expresión “x” más “y” igual a 30. En donde “x” representa un número y “y” representa el otro número.

El enunciado “su diferencia es 6”, se puede representar con la expresión algebraica “x” menos “y” igual a 6. En donde la letra “x” representa un número, y la letra “y”, el otro número, que son los mismos números utilizados en la expresión anterior.

De acuerdo con lo anterior, el sistema de dos ecuaciones lineales con dos incógnitas que resuelve el ejercicio es:

Una vez planteado el sistema, a continuación, se resolverá por el método de suma y resta.

Antes de exponer los pasos de ese método, se estudiarán algunos conceptos para darle un significado a esos pasos.

Observa que el sistema se compone de dos igualdades. Primero, analiza las igualdades por separado.

Comienza por la igualdad: “x” más “y” igual a 30, ¿qué valores de “x” y de “y” hacen de la igualdad un enunciado verdadero?

Por ejemplo, si “x” toma el valor de 30 y “y” toma el valor de cero, se cumple la igualdad “x” más “y” igual a 30, porque 30 más cero da como resultado 30.

Se dice entonces que el par ordenado 30 coma cero hace que se cumpla la igualdad.

Otro par ordenado que hace que se cumpla la igualdad es 29 coma 1, porque 29 más 1 es igual a 30.

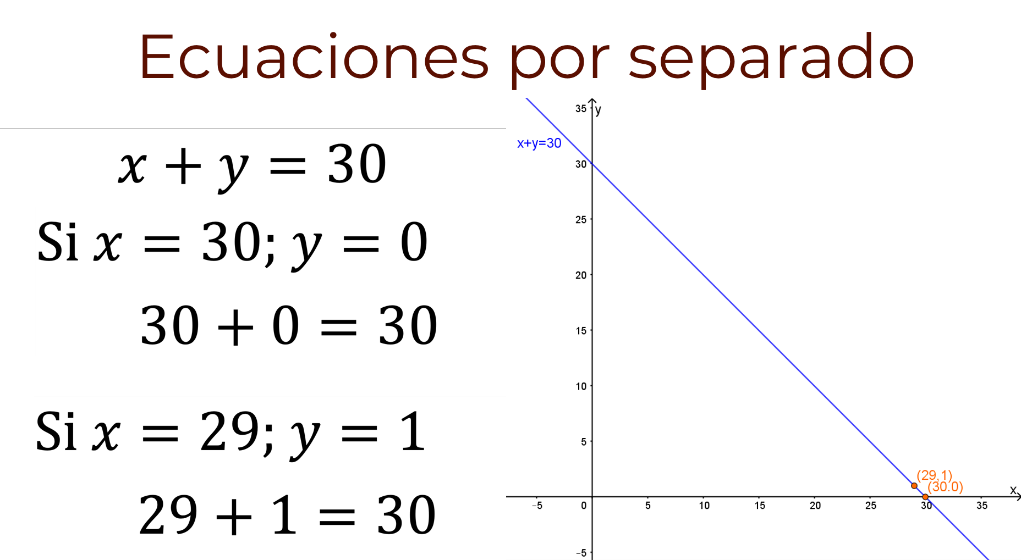
En un plano cartesiano, ¿cómo se pueden representar los valores de “x” y “y” que hacen que se cumpla la igualdad?

En un plano cartesiano, cada pareja ordenada que hace que se cumpla una expresión lineal, se puede representar con un punto.

En el caso de la igualdad “x” más “y” igual a 30, cada par ordenado que hace de la igualdad un enunciado verdadero, se puede representar con un punto sobre la recta “y” igual a 30 menos “x”.

Si se realiza un análisis similar para la igualdad, “x” menos “y” igual a 6, se llega a la conclusión de que los pares ordenados que cumplen con la igualdad se pueden representar como puntos sobre la recta “y” igual a “x” menos 6.

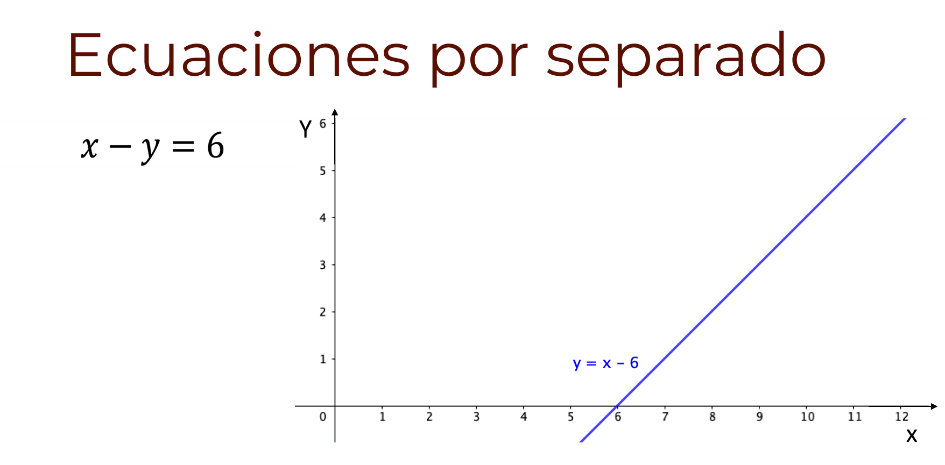
En resumen, si cada expresión lineal se analiza por separado, se pueden encontrar una infinidad de pares ordenados que hacen que se cumpla la igualdad.

Ahora bien, ¿qué es la solución de un sistema de ecuaciones lineales como “x” más “y” igual a 30 y “x” menos “y” igual a 6?

La solución de un sistema de ecuaciones se refiere a los pares ordenados que satisfacen. al mismo tiempo, todas las ecuaciones que lo conforman.

Por ejemplo, ¿el par ordenado 29 coma 1 es solución del sistema “x” más “y” igual a 30; “x” menos “y” igual a 6?

Se advierte que, si se sustituye “x” por 29 y “y” por 1, en la ecuación “x” más “y” igual a 30 se cumple la igualdad porque 29 más 1 es igual a 30.

Sin embargo, si se sustituye “x” por 29 y “y” por 1 en la ecuación “x” menos “y” igual a 6, no se cumple la igualdad porque 29 menos 1 es distinto de 6.

Así, el par ordenado 29 coma 1 no es solución del sistema porque al sustituirlos en las dos ecuaciones, no se verifican todas las igualdades al mismo tiempo.

Cada ecuación lineal del sistema, se representa en el plano por una recta. Todos los puntos de la recta representan los pares ordenados que hacen que se cumpla la igualdad.

Pero, al analizar las rectas como la representación de un sistema de ecuaciones, se buscan los pares ordenados que se encuentren en las dos rectas al mismo tiempo.

Por ejemplo, si se grafica el sistema “x” más “y” igual a 30; “x” menos “y” igual a 6, ¿qué punto o puntos se encuentran en las dos rectas al mismo tiempo?

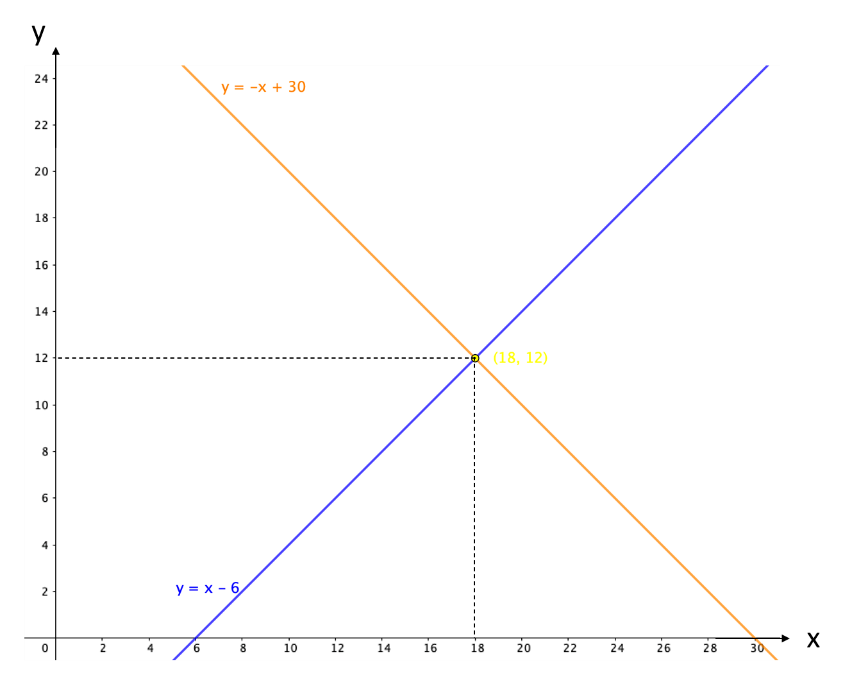
Se observa que, en este caso, las rectas coinciden en el punto 18 coma 12. Por tanto, el par ordenado 18 y 12 es solución del sistema.

Si sustituyes estos valores en las ecuaciones se observa que se cumplen las igualdades de 18 más 12 igual a 30 y 18 menos 12 igual a 6.

¿Cómo se puede encontrar ese punto algebraicamente? A continuación, se expondrá el método de suma y resta, y se le dará significado con base en lo que has aprendido.

En primera instancia, se puede observar que cada ecuación del sistema “x” más “y” igual a 30; “x” menos “y” igual a 6, contiene dos literales de las que se desconoce su valor llamadas incógnitas.

De acuerdo con lo que has estudiado en este grado ¿cómo consideras que se puede resolver el sistema de ecuaciones?

Uno de los métodos además del que acabas de utilizar es buscar un nuevo sistema de ecuaciones de tal forma que una de las ecuaciones sólo tenga una incógnita, pero al mismo tiempo, que tenga las mismas soluciones que el sistema original. Cuando dos sistemas tienen las mismas soluciones, se dice que son equivalentes.

¿Cómo se puede encontrar un sistema de ecuaciones que tenga las mismas soluciones que el sistema “x” más “y” igual a 30; “x” menos “y” igual a 6? En otras palabras ¿cómo se pueden encontrar sistemas equivalentes?

Una opción puede ser multiplicar ambos miembros de una de las ecuaciones del sistema por cualquier número distinto de cero.

Por ejemplo, considera nuevamente el sistema “x” más “y” igual a 30; “x” menos “y” igual a 6. Considera también que su representación gráfica consiste en dos rectas que se cortan en un punto.

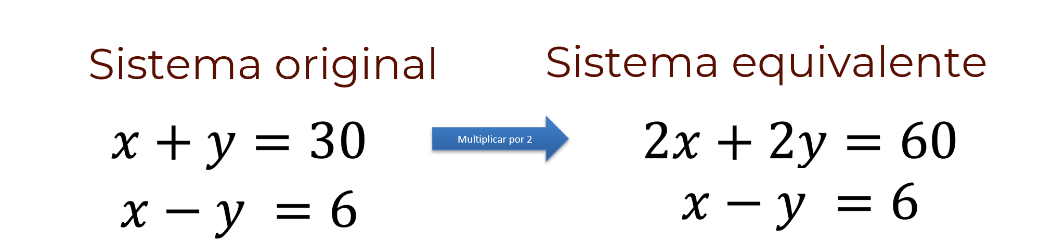
Ahora bien, si en el sistema, la ecuación “x” más “y” igual a 30 se multiplica por dos, se obtiene la expresión 2 “x” más 2 “y” igual a 60.

Aunque algebraicamente, las expresiones “x” más “y” igual a 30 y 2 “x” más 2 “y” igual a 60 puedan parecer dos ecuaciones distintas, los pares ordenados que hacen de las igualdades un enunciado verdadero son los mismos para ambas ecuaciones. Verifica esto para algunos valores.

En la gráfica, se puede observar que se trata de la misma recta y que, por tanto, el nuevo sistema tiene las mismas soluciones que el original, es decir, es equivalente.

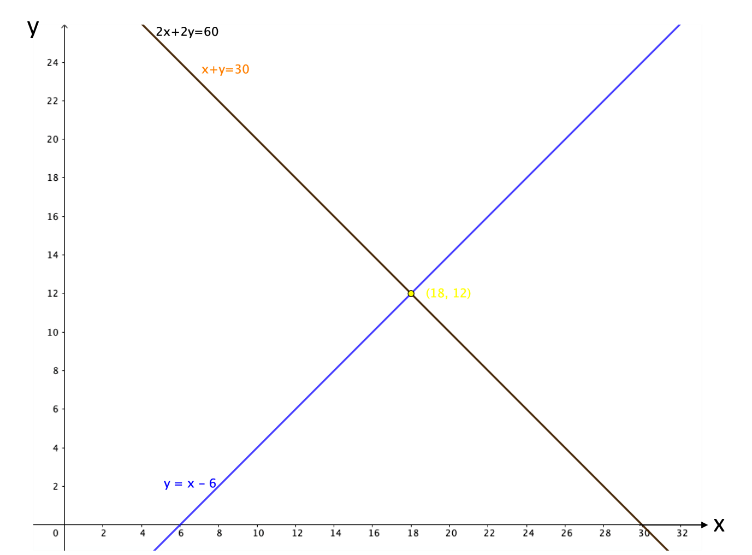
Otra opción consiste en sustituir una de las ecuaciones del sistema por la suma de ella con la otra.

Por ejemplo, en el sistema “x” más “y” igual a 30, “x” menos “y” igual a 6; realiza la suma de “x” más “y” igual a 30 y “x” menos “y” igual a 6.

Operando uno “x” más uno “x” da como resultado 2 “x”. Luego, uno “y” menos uno “y” es igual a cero “y”; por otro lado, 30 más 6 igual a 36. Por lo tanto, se obtiene la expresión 2 “x” igual a 36.

Ahora bien, si en el sistema “x” más “y” igual a 30, “x” menos “y” igual a 6; se sustituye la ecuación “x” menos “y” igual a 6 por la suma de las ecuaciones que se obtuvo: 2 “x” igual a 36; se obtiene el nuevo sistema “x” más “y” igual a 30, 2 “x” igual a 36.

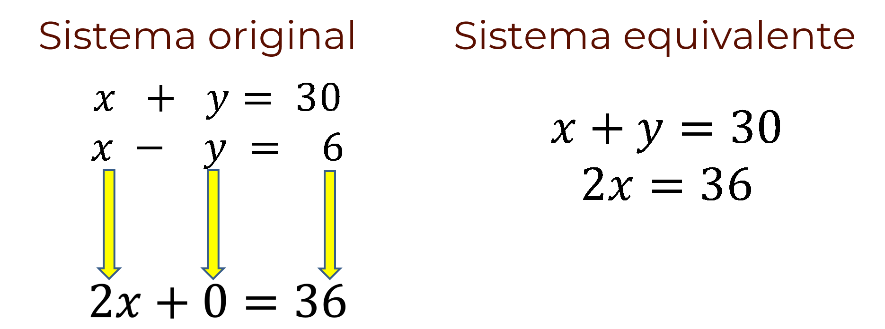
Observa que este nuevo sistema tiene las mismas soluciones que el original, es decir es un sistema equivalente al original. En la gráfica, se observa que las rectas del nuevo sistema se cortan en el punto 18 coma 12, como en el sistema original.

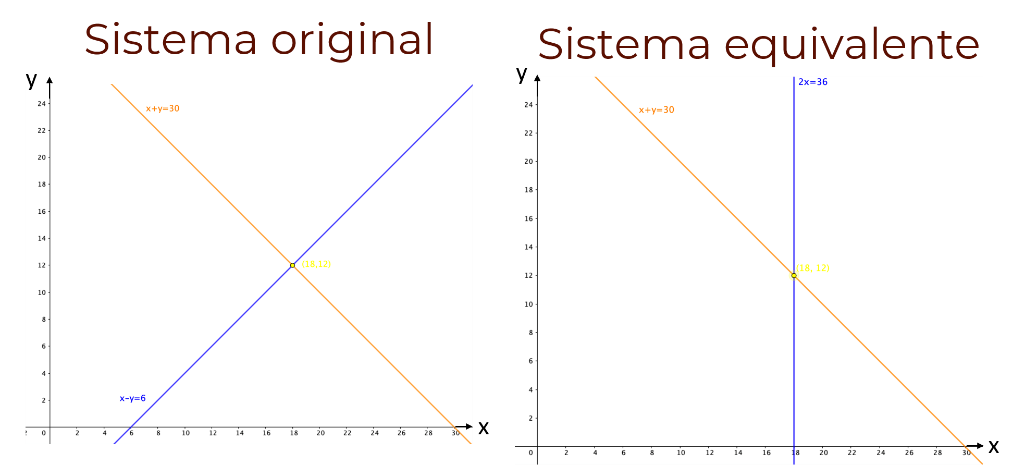
¿Qué ventajas tiene realizar las operaciones antes mencionadas para obtener sistemas lineales con la misma solución o soluciones?

Al elegir de manera adecuada las operaciones permitidas entre las ecuaciones, se puede obtener un nuevo sistema que contenga una ecuación lineal con una sola incógnita.

Esa ecuación se puede resolver con los métodos conocidos.

Por ejemplo, al realizar las operaciones permitidas entre las ecuaciones del sistema original, se obtuvo el nuevo sistema “x” más “y” igual a 30; 2 “x” igual a 36. En ese nuevo sistema, la ecuación 2 “x” igual a 36 se puede resolver con las propiedades de la igualdad:

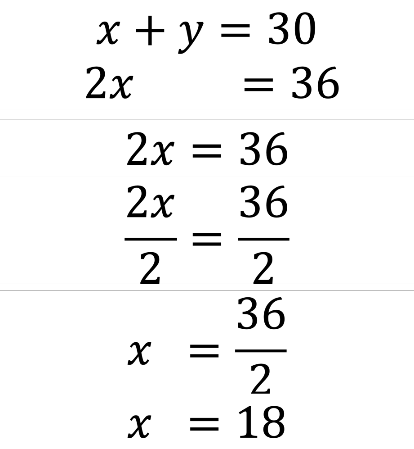
Se dividen ambos miembros de la igualdad entre el coeficiente de “x” que es 2, por lo tanto, se obtiene 2 “x” entre 2 igual a 36 entre 2. Si se realizan operaciones en el miembro izquierdo de la ecuación se tiene 2 “x” entre 2 es uno “x” que es igual a “x”. La ecuación que resulta es “x” igual a 36 entre 2. Si se realizan operaciones en el segundo miembro de la ecuación se divide 36 entre 2 y el cociente es igual a 18.

Así obtienes el valor de “x”, que es igual a 18.

Una vez que se conoce que el valor de “x” es 18, se puede conocer el valor de “y”. Para esto, se puede sustituir ese valor de la incógnita “x” en la primera ecuación del sistema: “x” más “y” igual a 30.

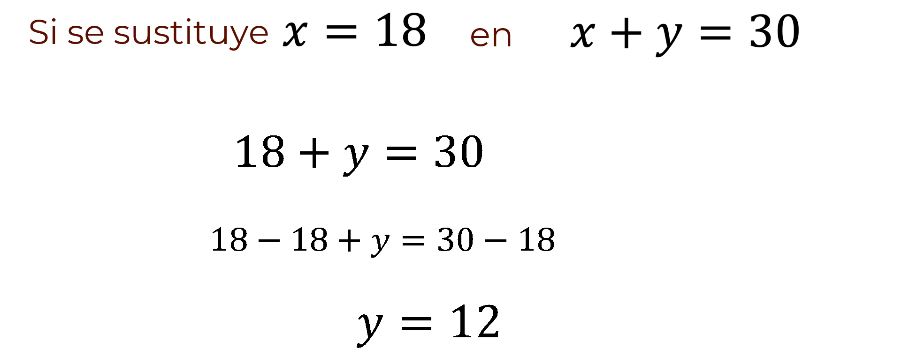
Sustituyendo, se tiene que 18 más “y” es igual a 30.

Por las propiedades de la igualdad, se puede restar 18 en ambos miembros de la ecuación, quedando 18 menos 18 más “y” es igual a 30 menos 18.

Al operar en el primer miembro, se obtiene 18 menos 18 da como resultado cero, más “y”, es decir, se obtiene únicamente “y”. Al operar en el segundo miembro se obtiene, 30 menos 18, es igual a 12.

Así, el valor de la incógnita “y” es igual a 12.

Entonces, la solución del sistema es:

“x” igual a 18 y “y” igual a 12

Por lo tanto, un número es 18 y el otro es 12.

Has aprendido que, se pueden realizar operaciones permitidas entre las ecuaciones de un sistema, de forma que, por un lado, se pueda obtener uno nuevo con las mismas soluciones que el original y que, por otro lado, el sistema obtenido tenga la ventaja de que una de las ecuaciones se encuentre en términos de una sola incógnita.

Al resolver esa ecuación, es posible conocer el valor de una de las incógnitas. Una vez que se obtiene dicho valor, se puede sustituir en la otra ecuación del sistema para obtener el valor de la otra incógnita.

Este método, suele presentarse en forma de pasos:

1. Multiplicar ambas ecuaciones del sistema por números, de tal forma que se tengan términos iguales con la misma incógnita, pero con signos opuestos.

2. Sumar las ecuaciones.

3. Resolver la ecuación obtenida.

4. Sustituir el valor hallado en una de las ecuaciones para obtener el valor de la otra incógnita.

Ahora que ya has dado un significado a esos pasos. Responde, ¿en qué casos utilizarías este método?

Una vez que se hallan los valores de las incógnitas, se sustituirán en las ecuaciones del sistema de dos ecuaciones lineales con dos incógnitas, para verificar que las igualdades se cumplen.

Se sustituye el valor numérico de “x” igual a 18 y “y” igual a 12 en las dos ecuaciones.

Se comenzará sustituyendo los valores numéricos de “x” y de “y”, en la primera ecuación, que es: “x” más “y” igual a 30.

Sustituyendo los valores se obtiene: 18 + 12 = 30. Si se realiza la suma de 18 + 12 se obtiene como resultado 30. Se observa que 30 es igual a 30.

En segundo lugar, se sustituyen los valores numéricos de “x” y de “y” en la segunda ecuación, que es: “x” menos “y” igual a 6.

Al sustituirlos, se obtiene: 18 menos 12 igual a 6. Al realizar la operación se obtiene 6. Se observa que 6 es igual a 6.

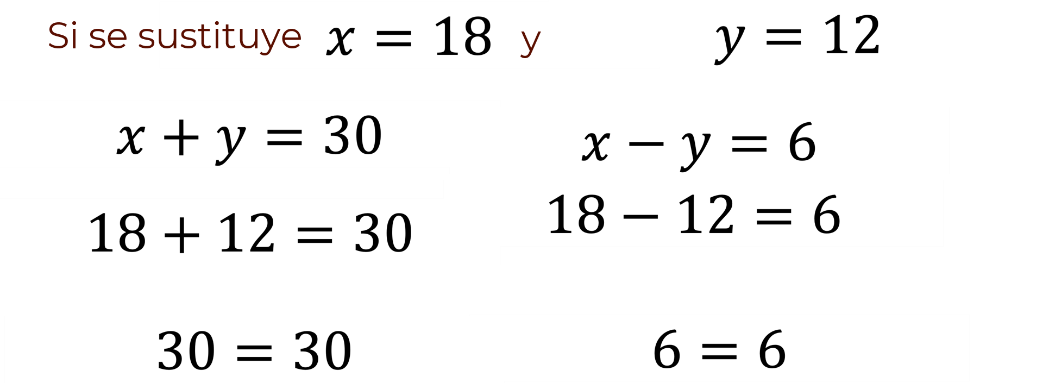
Así, se verifica que los valores numéricos de las literales “x” y “y”, satisfacen ambas ecuaciones del sistema.

A continuación, resuelve el siguiente ejercicio para aplicar lo aprendido.

Primero realiza una estimación: ¿Se llenaron más botellas con una capacidad de 5 litros que de 2 litros?

Ahora, procede a modelar el ejercicio con un sistema de dos ecuaciones lineales con dos incógnitas.

Se asignará la letra “x” al número de botellas con capacidad de 5 litros, y “y” al número de botellas con capacidad de 2 litros.

La primera ecuación del sistema es “x” más “y” igual a 323, donde “x” representa el número de botellas con capacidad de 5 litros, “y” el número de botellas con capacidad de 2 litros y 323 el número total de botellas.

La segunda ecuación del sistema se puede representar como 5 “x” más 2 “y” igual a mil, donde 5x representa la cantidad total de detergente envasada en las botellas de 5 litros, mientras que 2x representa la cantidad total envasada en botellas de 2 litros y 1,000 litros es la cantidad total de detergente.

El sistema de dos ecuaciones con dos incógnitas queda:

La primera ecuación: “x” más “y” igual a 323.

La segunda ecuación: 5 “x” más 2 “y” igual a 1,000.

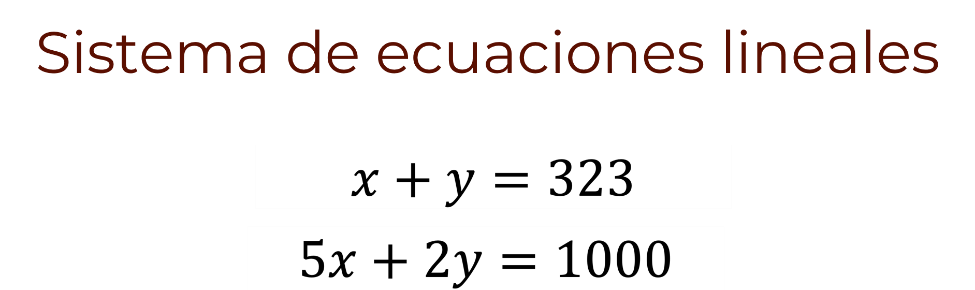
Una manera de continuar con la resolución del problema consiste en encontrar un nuevo sistema de ecuaciones que sea equivalente al original, pero que contenga una ecuación con únicamente una incógnita.

¿Qué operaciones están permitidas para encontrar el sistema equivalente?

Como se dijo anteriormente, una operación permitida consiste en multiplicar ambos miembros de una de las ecuaciones del sistema por cualquier número distinto de cero.

Otra operación permitida consiste en sustituir una de las ecuaciones del sistema por la suma de ella con la otra. Esa otra ecuación se puede multiplicar por cualquier número.

Reflexiona, ¿qué operaciones permitidas pueden realizar entre las ecuaciones del sistema “x” más “y” igual a 323; 5 “x” más 2 “y” igual a 1 000, para encontrar un nuevo sistema de ecuaciones equivalente, pero que contenga una ecuación con únicamente una incógnita?

Una opción es multiplicar la ecuación “x” más “y” igual a 323 por 2 negativo.

Realizando la operación, se obtiene: 2 negativo por uno “x” dando como resultado 2 “x” negativo; luego, 2 negativo por uno “y” da como resultado 2 “y” negativo y al multiplicar 2 negativo por 323 se obtiene 646 negativo.

Así, se obtiene el nuevo sistema conformado por las ecuaciones 2 “x” negativo menos 2 “y” igual a 646 negativo y 5 “x” más 2 “y” igual a mil.

Recuerda que, al realizar las operaciones permitidas, este nuevo sistema tiene las mismas soluciones que el original. Es decir, este sistema es equivalente al original. Pero todavía no se obtiene un sistema en el que una de las ecuaciones contenga únicamente una incógnita.

De acuerdo con las operaciones permitidas, en el sistema conformado por las ecuaciones 2 “x” negativo menos 2 “y” igual a 646 negativo y 5 “x” más 2 “y” igual a 1,000, una de las ecuaciones se puede sustituir por la suma de ella con la otra ecuación del sistema.

Al sumar 2 “x” negativo menos 2 “y” igual a 646 negativo más 5 “x” más 2 “y” igual a 1,000, se tiene que, 2 “x” negativo más 5 “x” da como resultado 3 “x”; 2 “y“ negativo más 2 “y” igual a cero; y 646 negativo más 1,000 es igual a 354. Por lo tanto, se obtiene la ecuación 3x igual a 354.

En el sistema conformado por las ecuaciones, dos “x” negativo menos dos “y” igual a 646 negativo y 5 “x” más 2 “y” igual a 1,000, se puede sustituir la ecuación 5 “x” más 2 “y” igual a 1,000 por la ecuación 3 “x” igual a 354.

Así, se obtiene un nuevo sistema conformado por las ecuaciones dos “x” negativo menos dos “y” igual a 646 negativo y 3 “x” igual a 354. Ese sistema es equivalente al original, pero tiene la ventaja de que contiene una ecuación con únicamente una incógnita.

En ese nuevo sistema, se puede resolver la ecuación 3 “x” igual a 354 aplicando las propiedades de la igualdad:

Se divide ambos miembros de la ecuación entre el coeficiente de “x” que es 3, por lo tanto, se obtiene 3 “x” entre 3 igual a 354 entre 3. Al dividir 3 “x” entre 3 se obtiene uno “x” igual a “x”. Al dividir 354 entre 3, el cociente es igual a 118.

Así, se obtiene el valor de la incógnita “x” es igual a 118.

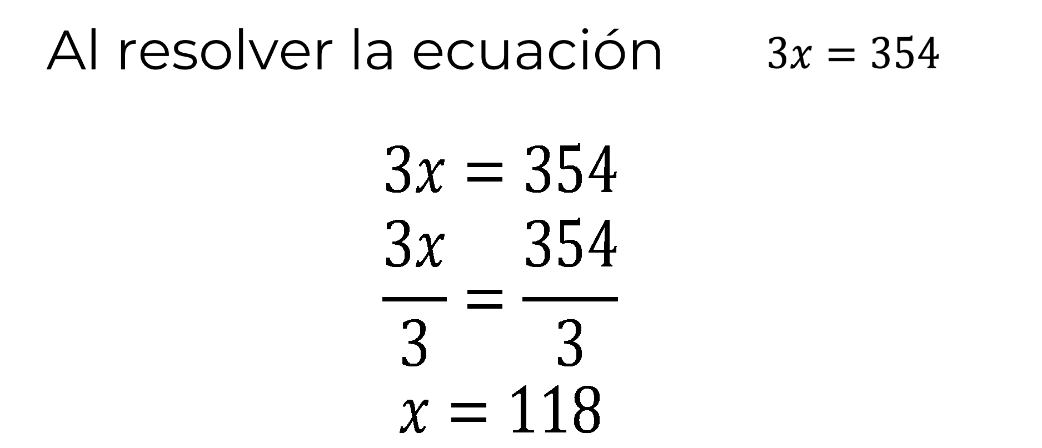
Ahora, una vez que ya se obtuvo el valor de la incógnita “x” se puede calcular el valor de la incógnita “y”.

Piensa ¿qué harías para obtenerla?

Se puede sustituir el valor obtenido para “x” en la otra ecuación del sistema equivalente que es 2 “x” negativo menos 2 “y” igual a 646 negativo o en la ecuación original x + y = 323.

Resuelve la ecuación que resulta para calcular el valor de “y”. Se obtiene “y” igual a 205.

La solución del sistema es:

“x” igual a 118

“y” igual a 205

Esto significa que, el número de botellas de 5 litros que se ocuparon es igual a 118 y el de 2 litros es igual a 205.

Comprueba estos resultados. Observa las ecuaciones originales:

“x” más “y” igual a 323 y 5 “x” más 2 “y” igual a 1,000.

Al sustituir los valores obtenidos para “x” y para “y” se tiene, para la primera ecuación: 118 más 205 igual a 323. 118 más 205 es igual a 323. Observa que se cumple la igualdad.

En la segunda ecuación se tiene 5 por 118 más 2 por 205 es igual 1,000. Al calcular los productos se obtiene que 5 por 118 es igual a 590 y que 2 por 205 es igual a 410. Al sumar 590 más 410 se obtiene 1,000. En esta ecuación también se cumple la igualdad.

Regresa a la estimación que hiciste al inicio de este problema, ¿qué tanto te aproximaste a la respuesta correcta? Ahora, ya sabes que las botellas de dos litros se ocuparon más en el envasado.

Una vez que ya se encontraron los valores de las literales, puedes verificar que, al sustituir esos valores en el sistema de dos ecuaciones lineales con dos incógnitas, se obtienen igualdades.

En ella, se modelaron problemas con sistemas de ecuaciones lineales con dos incógnitas, los cuales se resolvieron por el método de suma y resta.

¡Buen trabajo!

Gracias por tu esfuerzo.

Descarga tu clase dando clic aquí