Medidas de tendencia central

Medidas de tendencia central

Aprendizaje esperado: usa e interpreta las medidas de tendencia central (moda, media aritmética y mediana), el rango y la desviación media de un conjunto de datos y decide cuál conviene más en el análisis de los datos en cuestión.

Énfasis: usar e interpretar las medidas de tendencia central en un conjunto de datos y determinar cuál es la más conveniente para representarlos.

¿Qué vamos a aprender?

En esta sesión, profundizarás en el estudio de las medidas de tendencia central. Para ello, analizarás múltiples casos para determinar cuándo una medida es más adecuada para representar un conjunto de datos.

¿Qué hacemos?

Reflexiona sobre las siguientes preguntas:

1. Fuera del ambiente escolar, ¿alguna vez has contestado alguna encuesta?
2. ¿Has participado de alguna manera en el análisis de datos para que alguien más pueda calcular la media aritmética, la mediana o la moda?

Retomando la primera pregunta, puede que hayas contestado que sí, pues en algunos casos, en los supermercados o en internet, hay personas que realizan encuestas sobre la satisfacción de algún producto, o en otros casos, se realizan llamadas telefónicas para conocer las preferencias sobre algunos servicios o la satisfacción del cliente.

Si tu respuesta fue negativa en la primera pregunta, es probable que sí hayas participado a través de tus interacciones en la recopilación de información por un tercero.

Analiza por qué con la siguiente pregunta: “¿has participado de alguna manera en el análisis de datos para que alguien más pueda calcular la media aritmética o la mediana o la moda?”.

La mayoría de las personas ha participado en la recolección de datos sin darse cuenta. Por ejemplo, si en algún momento del día interactúas con alguna red social o escuchas alguna canción en algún servicio digital de música, ya sea adelantando la canción o escuchándola varias veces, entonces ya colaboraste con la estadística.

Muchos servicios digitales recopilan información cada que se interactúa con ellos, compilando datos que al ser analizados forman parte de una estadística; por ejemplo, el tiempo que se invierte escuchando música diariamente, la canción que más se escucha, el lugar en donde se escucha música. Incluso tienen algoritmos que cuantifican qué canciones no te gustan para evitar colocarlas como sugerencia.

Otro ejemplo es que, al final de cada año existe un servicio digital de música que proporciona información a cada usuario, mostrando en primer lugar el género de música que más escuchó. Observa la siguiente imagen.

En la imagen se muestra que el género que más se escuchó durante el año fue el rock y esta información fue recopilada de un solo usuario.

Reflexiona: ¿qué medida de tendencia central representa el género de música más escuchado por este usuario?

Antes de responder la pregunta, analiza la siguiente situación. Imagina que durante un día otro usuario escuchó 10 canciones que pertenecen a los siguientes géneros:

• Canción 1. Electrónica
• Canción 2. Rock
• Canción 3. Electrónica
• Canción 4. Pop
• Canción 5. Electrónica
• Canción 6. Rock
• Canción 7. Electrónica
• Canción 8. Electrónica
• Canción 9. Pop
• Canción 10. Rock

¿Se puede obtener la media aritmética de los datos anteriores?

Tal y como se presentan los géneros de las 10 canciones que escuchó este usuario, no es posible obtener la media aritmética, ¿te imaginas cuál puede ser la suma de todos ellos?, ¿puedes imaginar cuál es el cociente al dividir esa suma entre 10?

Por no ser datos cuantificables, se puede descartar la media aritmética como dato representativo, dado que ni siquiera se puede calcular.

Al ordenar los géneros de menor a mayor, de acuerdo con la cantidad de veces que fue escuchado, ¿qué dato sería la mediana?, ¿será de utilidad la mediana para encontrar el dato representativo?

Como sabes, para determinar la mediana, se deben ordenar los datos. En este caso, se ordena de menor a mayor el número de veces que se escucharon en el día. Así se ubica el dato o los datos centrales, que en este caso son rock y electrónica. Observa que quedaron 4 datos del lado izquierdo y 4 datos del lado derecho.

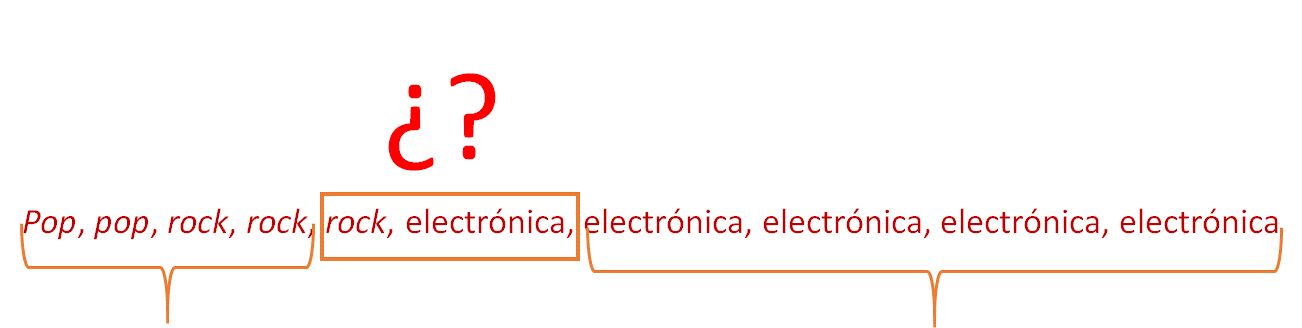
Cuando 2 datos están en el centro del conjunto total, se calcula su promedio para obtener la mediana, pero ¿cuál es el promedio de rock y electrónica?, ¿es posible calcularlo?

Como puedes observar, no es posible obtener un promedio de estos datos y, por lo tanto, tampoco se podría determinar la mediana o usarla como dato representativo.

Entonces, ¿qué medida de tendencia central puede describir el género de música más escuchado en ese día?

La moda es la medida de tendencia central que resulta pertinente para describir este conjunto de datos, ya que indica que la música electrónica fue la que más veces escuchó.

Existen varias maneras de responder encuestas o interactuar para generar datos que posteriormente tú u otras personas analizarán. Al hacer uso de medios digitales, se genera información, por ejemplo, la canción que más se escucha.

Sin embargo, no todas las medidas de tendencia central son de utilidad para describir un conjunto de datos. En el ejemplo anterior no fue posible calcular el promedio y la mediana de los datos, pero la moda permitió identificar el dato representativo relacionado con la mayor frecuencia.

Analiza otra situación.

El rendimiento de Mía Fernanda en la escuela está bajando. La orientadora educativa de Mía Fernanda le pidió escribir las actividades que realizó de lunes a viernes de la semana pasada, así como el tiempo destinado a cada una de ellas.

A continuación, se muestra lo que Fernanda anotó.

Aunque pueden existir múltiples factores que influyan en el rendimiento escolar de Fernanda, la orientadora educativa se dio cuenta de algo y decidió redactar un mensaje a la mamá de Fernanda.

Analiza los datos que faltan en el mensaje y determina qué medida de tendencia central es pertinente para reportar la situación de Fernanda. La nota es la siguiente.

En el renglón que dice: “Su horario de estudio no es constante porque”. ¿Con qué frase consideras más pertinente completar el enunciado?

1. En promedio estudia 2 punto 2 horas al día.
2. En dos días estudió 3 horas.

Al analizar la cantidad de horas que estudió por día, se puede notar que el jueves no estudió y que el viernes dedicó 1 hora a esa actividad. Estos datos se encuentran alejados de lo que estudió de lunes a miércoles, por lo cual no es posible decir que diariamente estudia cierta cantidad de tiempo.

Ordenando los datos de menor a mayor, se tiene que estudió: 0 horas, 1 hora, 3 horas, nuevamente 3 horas y, por último, 4 horas. Observa que tanto la mediana como la moda coinciden en 3 horas. Entonces, ¿qué dato usarías para reportar la situación del horario para estudiar de Fernanda?

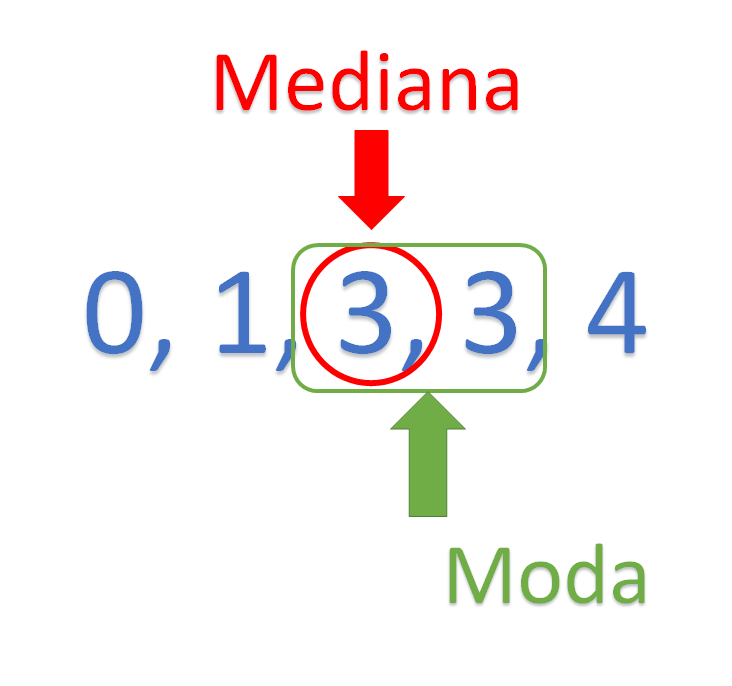
Ahora, completa el renglón que dice: “Veo de manera positiva que contribuya en las labores del hogar, ya que”. Y para ello elige la mejor opción que represente los datos de sus horarios para hacer sus deberes en el hogar.

1. Suele emplear 2 horas al día.
2. En promedio, invierte 1 punto 8 horas al día.

Se puede observar la media, la mediana y la moda de las horas que Mía Fernanda contribuye en las labores de su hogar. Aunque ambas opciones permiten completar el texto, es preferible usar la primera opción, ya que la moda y la mediana representan mejor el tiempo que emplea para hacer sus deberes en el hogar.

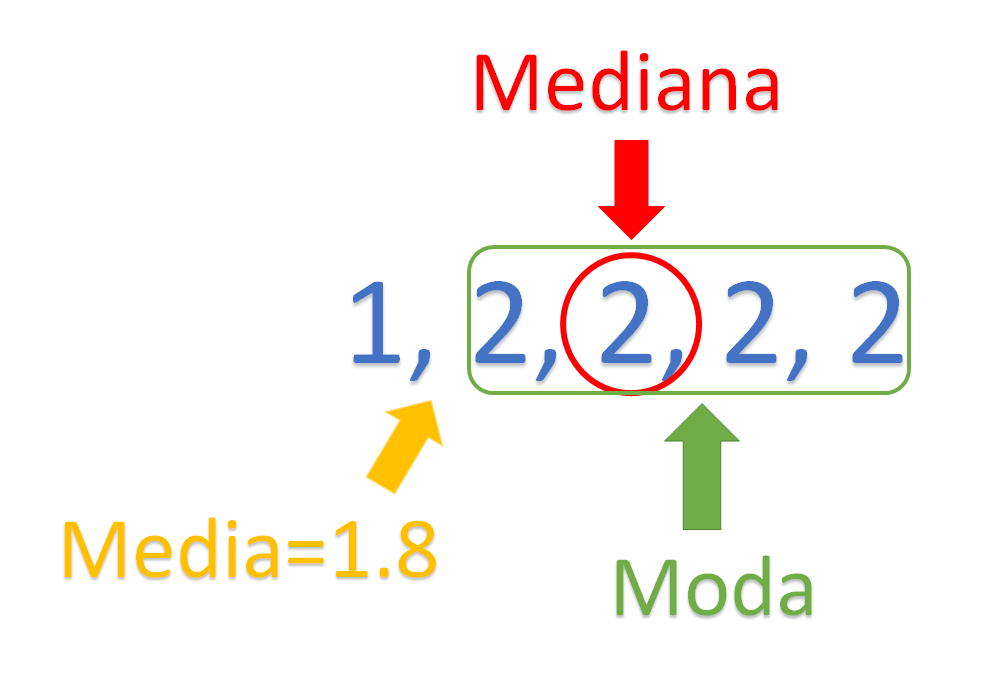
Completa el último renglón: “Es necesario modificar el tiempo que pasa viendo videos en las redes sociales porque”.

1. No existe una moda en sus horarios para ver videos.
2. En promedio invierte 8 horas días viendo videos.

La segunda opción representa mejor los horarios que usa para ver videos en la red social, ya que coincide con la media aritmética y con la mediana.

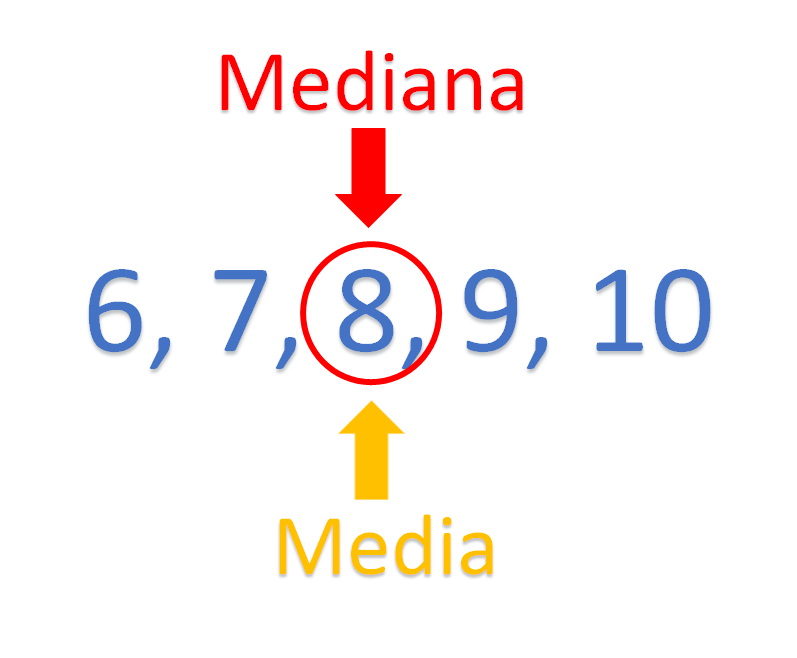
Aunque pueden existir muchos factores para que el rendimiento académico de Mía Fernanda esté bajando, se puede identificar un área de oportunidad en el tiempo que invierte mirando videos en su red social. ¿

En tu caso: ¿cómo distribuyes tu tiempo? Analiza la distribución de tu tiempo y toma decisiones que te ayuden a mejorar tu rendimiento y destina tiempo para cumplir con tus deberes dentro de tu hogar. También considera que el tiempo que pases en las redes sociales no consuma tiempo que puedas destinar a otras actividades más importantes.

Existen ambientes virtuales en donde las personas, por su propia voluntad y conscientes de ello, contribuyen con datos estadísticos que ayudan a más personas.

Observa el siguiente ejemplo.

Maximiliano desea ir de vacaciones con su esposa Gala. Ambos valoran varias opciones de transporte y prestan especial atención a las opiniones que han hecho algunos de los usuarios de los servicios que recibieron por parte de la empresa.

Esta valoración comúnmente se hace eligiendo la cantidad de “estrellas” que se dará por el servicio, donde 1 estrella puede representar un pésimo servicio, 3 estrellas puede representar un servicio regular y 5 estrellas puede representar un excelente servicio.

Observa lo que ellos encontraron.

¿Cuál opción elegirías?

Si no se considera la cantidad de usuarios que valoraron el servicio, se podría pensar que el autobús azul es la mejor opción, ya que tiene 10 estrellas.

Con lo que has estudiado sobre medidas de tendencia central, sabes que es necesario considerar todos los datos, así que analiza a detalle las valoraciones.

Para el autobús rojo sólo se tiene una valoración, por lo que, al ser el único dato, no es posible compararlo con las opiniones de otros usuarios. Una posibilidad es considerar a ese único dato la media, la mediana y la moda. Observa qué pasa en este caso.

Max y Gala decidieron que era conveniente analizar más opciones. Para el autobús verde un usuario calificó con 4 estrellas, 600 con 3 estrellas y 1 con 1 estrella. ¿Cuál es su media, mediana y moda?

Sumando las estrellas, el total es de 1,805 y dividiendo entre el total de los usuarios que valoraron el servicio, la media aritmética es 2.9 estrellas. Asimismo, la mediana y moda son 3 estrellas.

Por otra parte, el autobús azul fue calificado con 5 estrellas por 10 usuarios, 2 estrellas por 200 usuarios y 1 estrella por 300 usuarios.

¿Cuál es su media, mediana y moda?

Sumando el total de estrellas, el resultado es 750, entre el total de usuarios que valoraron el servicio, se obtiene 1 punto 4 estrellas como media aritmética, con una mediana y moda de 1 estrella.

Tomando como referencia lo anterior, las medidas de tendencia central de los 3 autobuses son las siguientes.

Ahora, reflexiona en las siguientes preguntas:

• ¿Qué decidirías?
• ¿Elegirías el autobús rojo porque pareciera que sus medidas de tendencia central son más altas que los demás?
• ¿Elegirías el autobús azul porque tiene más valoraciones de 5 estrellas?
• ¿Elegirías el autobús verde porque tiene más usuarios que han valorado el servicio con una media mayor que el autobús azul?

En ejemplos como el anterior se puede observar la necesidad de contar con el mayor número de datos que permitan obtener mejores referencias, tanto de la opinión de los usuarios del servicio como de la calidad de los servicios.

Maximiliano y Gala deberán elegir una de las tres opciones y ellos eligieron el autobús verde; ¿qué razones consideras que los llevaron a elegir ese autobús? Reflexiona sobre esta pregunta y comparte tus argumentos con tus profesores cuando sea posible.

Es importante conocer el significado de cada una de las medidas de tendencia central. George Bernard Shaw dijo:

“La estadística es una ciencia que demuestra que, si mi vecino tiene dos coches y yo ninguno, los dos tenemos uno."

George Bernard Shaw

¿Qué te parece esa frase?, ¿en qué se basará George Bernard Shaw para afirmar esto?

Como seguramente identificaste, él está haciendo referencia a la media aritmética. Analiza la frase. George hace referencia a dos personas: su vecino y él. Su vecino tiene 2 coches y George, ninguno. No hay moda en este conjunto de datos porque los dos datos tienen la misma frecuencia.

La mediana y la media de estos dos datos se obtiene de la misma manera, adicionándolos y dividiendo la suma entre 2; por lo tanto, cero más 2 es igual a 2, entre 2, es igual a 1. Es por esta razón que George menciona que, si su vecino tiene 2 coches y él ninguno, entonces estadísticamente él también tendrá 1.

Otra frase sobre estadística útil para analizar es la que dijo Eduardo Sáenz de Cabezón. Menciona lo siguiente:

“¿Sabías que tengo más ojos que la media de la población? […] lo que pasa es que el dato ese de la media de ojos no es algo muy descriptivo de la población, de hecho, es un dato inútil."

Eduardo Sáenz de Cabezón

A diferencia del ejemplo de George, donde sólo había dos personas, en el ejemplo de Eduardo hay miles de millones de personas, ya que hace referencia a la población mundial.

¿Por qué afirma que tiene más ojos que la media de la población? Analiza esta situación.

Si hay 5 personas con 2 ojos, la media aritmética será de 2.

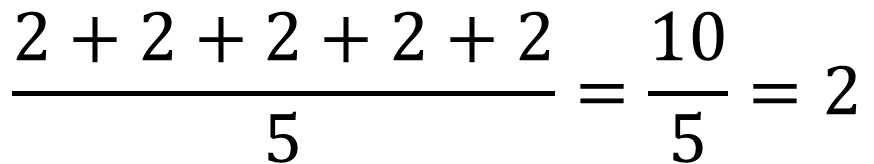
Pero si se agrega 1 persona que por algún accidente haya perdido un ojo, la media aritmética de las seis personas ya no sería 2, sino aproximadamente 1 punto 8.

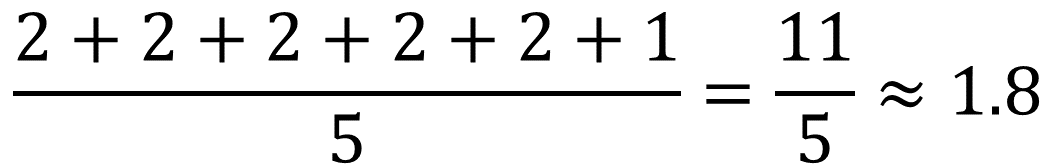
Es entonces que cualquiera de las primeras 5 personas ya tendría más ojos que la media de esas 6 personas.

Con los análisis anteriores se enfatiza que las medidas de tendencia central son de gran utilidad para analizar un conjunto de datos y pueden ayudar a tomar mejores decisiones. Analiza otro ejemplo.

El dueño de una paletería registró los litros de agua que vendió durante una semana, incluyendo el domingo, donde tuvo un caso excepcional, ya que surtió un pedido de 40 litros de agua de horchata y 40 litros de agua de jamaica. En la siguiente tabla se muestra este registro.

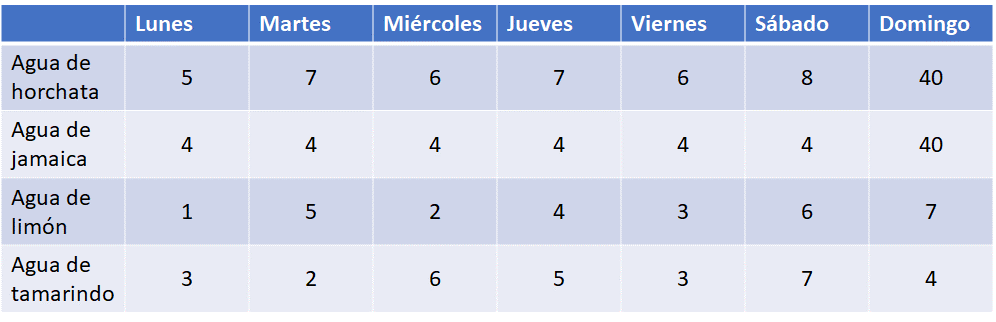
¿Qué medida de tendencia central representará mejor su venta diaria de agua de horchata?

Como puedes observar, el domingo tuvo un caso excepcional, pues surtió un pedido de 40 litros de agua de horchata. Si tú fueras el dueño de la paletería, en una semana donde no hay pedidos especiales, ¿cuántos litros de agua prepararías al día?

Si se calcula la media aritmética de los litros de agua de horchata que vendió en esa semana, se obtienen aproximadamente 11.2 litros.

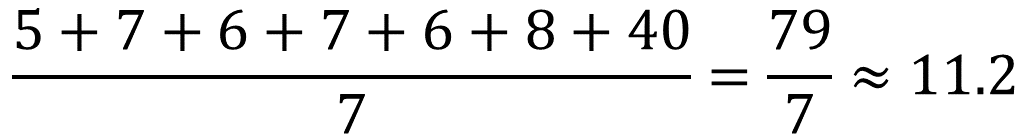
La mediana es 7 litros, mismo que coincide con una de las dos modas.

Es momento de tomar decisiones; ¿alrededor de cuántos litros de agua de horchata prepararías cada día? Ten presente que es un artículo perecedero, es decir, que no es conveniente mantenerlo tanto tiempo almacenado porque pierde la calidad de sus ingredientes o se echa a perder, como comúnmente se dice.

Una sugerencia es considerar la mediana como dato representativo para preparar alrededor de 7 litros, porque si se considera la media aritmética, se puede tener diariamente un excedente de agua que haría perder ganancias, ya que esta medida se ve afectada por los valores extremos, por ejemplo, el pedido especial de 40 litros de agua.

Con respecto al agua de jamaica, ¿qué decisión tomarías?

En los litros que se vendieron de agua de jamaica también se cuenta con un dato atípico, debido al pedido que hicieron el domingo, con lo cual se obtiene una media aritmética aproximada a 9.1 litros.

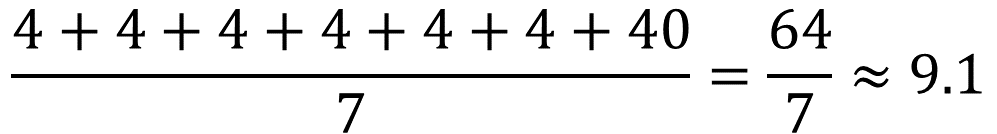
Pero si se analizan los datos de lunes a sábado, es posible observar que tanto la moda como la mediana es de 4 litros, lo que parecería mostrar que diariamente vende esa cantidad de litros; entonces, ¿cuántos litros de agua de jamaica prepararías diariamente?

La mejor opción podrías ser preparar 4 litros diarios.

Respecto al agua de limón, se identifica que no existe un dato atípico y que ningún dato se repite; entonces no hay moda en este conjunto de datos, porque ninguno se repite.

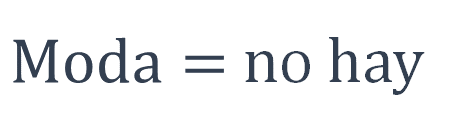
¿Cuántos litros de agua prepararías diariamente? Si analizas las medidas de tendencia central, tendrás más elementos para decidir. Como en la media aritmética, el 4 representa el conjunto de datos, mismo que coincide con la mediana. La mejor opción sería preparar 4 litros de agua de limón.

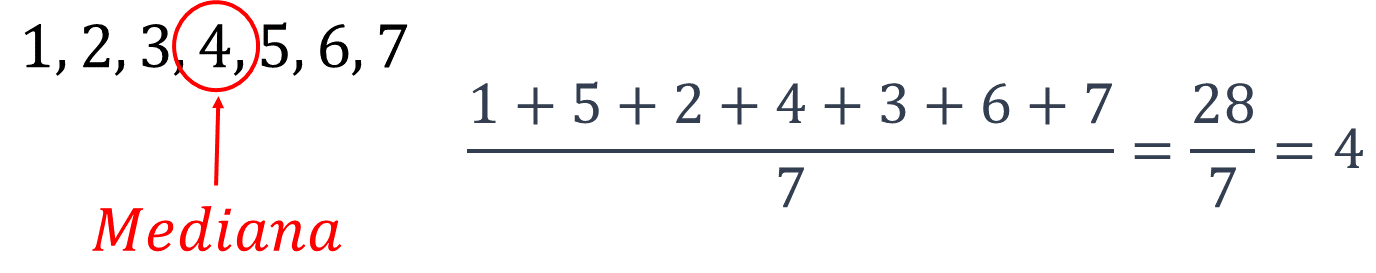
Por último, analiza el caso del agua de tamarindo, donde tampoco existe un dato atípico. A simple vista y sin hacer cálculos, ¿cuántos litros de agua prepararías diariamente?

Calcula las medidas de tendencia central de este conjunto de datos.

Para el agua de tamarindo la media aritmética de los litros de agua vendidos es aproximadamente 4.2 litros.

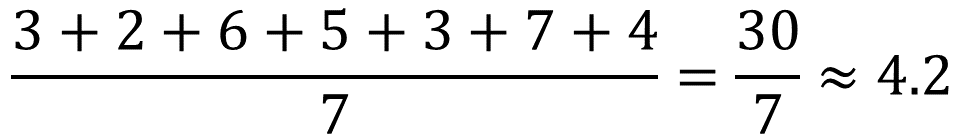
Mientras que la mediana es de 4 litros, y la moda de 3 litros.

Puedes observar que las medidas de tendencia central son diferentes entre sí. ¿Qué dato te resultaría significativo?, ¿cuántos litros de agua de tamarindo prepararías diariamente?, ¿podrías sustentar la decisión en los datos que matemáticamente se calcularon o recurrirías a una apreciación subjetiva basada en lo que se pueda suponer?

La mejor opción podría ser preparar 4 litros de agua, ¿coindices con la respuesta? Arguméntala y, cuando sea posible, compártetela con alguien más.

Haciendo un resumen de lo estudiado en esta sesión, existen múltiples casos donde las medidas de tendencia central pueden no describir de manera adecuada una población o conjunto de datos.

De igual manera, reconociste cuándo una medida de tendencia central es más adecuada para representar un conjunto de datos, como en el caso de los géneros musicales, que se trató de datos cualitativos.

Con esto has finalizado esta sesión. Recuerda que este es un material de apoyo y para complementar lo estudiado, puedes consultar otras fuentes, como tu libro de texto de Matemáticas de segundo grado.

El reto de hoy:

Resuelve algunos de los problemas o ejercicios sobre las medidas de tendencia central. Para ello, consulta tu libro de texto de Matemáticas de segundo grado.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html