¿Mediana o media aritmética?
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:57
¿Mediana o media aritmética?
Aprendizaje esperado: uso de la media (promedio), la mediana y la moda en la resolución de problemas.
Énfasis: reflexionar acerca de cuándo es más representativa la media aritmética que la mediana para un conjunto de datos.
¿Qué vamos a aprender?
Aprenderas a emplear la media (promedio), la mediana y la moda en la resolución de problemas, lo que te permitirá reflexionar acerca de cuándo es más representativa la media aritmética que la mediana para un conjunto de datos.
Vas a necesitar tu libro Desafíos sexto grado, desafío 53, páginas 105 y 106, tu cuaderno u hoja para tomar notas, lápiz, goma, sacapuntas y mucha disposición.

https://libros.conaliteg.gob.mx/P6DMA.htm?#page/105
¿Qué hacemos?
Iniciaremos la sesion revisando la petición de César, un estudiante, que expone dos dificultades que se le presentaron al calcular el valor de la media aritmética y la mediana de un conjunto de datos estadísticos.

Observa qué dice la nota que un alumno presenta los registros que hizo para comprender más sobre la obtención y uso de las medidas de tendencia central.
Hola mi nombre es César Uriel curso el sexto grado en la Primaria Defensores de la República. Debido a la pandemia del COVID 19 he continuado con mi actividad académica desde mi casa a través de la computadora y la televisión y a mis padres les preocupa que no esté dedicando el debido tiempo de estudio, pero yo considero que hasta ha aumentado y cada vez más dedico menos tiempo a actividades no escolares. Para demostrarlo he registrado el tiempo que dedico a actividades escolares durante las últimas dos semanas.

Observa que en la tabla registra, durante diez días, las horas que César ha estado dedicado a actividades escolares, por ejemplo, en la primera semana, el lunes anotó 6 horas, el martes, cuatro horas, el miércoles, seis horas; el jueves registró cinco horas y el viernes otra vez anotó seis horas.
En la segunda semana, el lunes registró ¿cero horas? Es eso posible. Sí, es posible, podemos interpretarlo como un día que no hizo nada o que no tuvo actividad escolar. Es cierto, ya el martes registró cinco horas y el miércoles aumentó a ocho horas, para jueves y viernes registró cuatro y seis horas.
Esos son los diez registró que César hizo, pero qué más nos dice en su carta.
Y de acuerdo con lo que estudiamos en la clase anterior, me dispuse a calcular los valores de la moda, media aritmética y mediana de este conjunto de datos para resumirlo y presentarlo, sin embargo, tuve dos dificultades.
La primera dificultad fue determinar el valor de la mediana porque al ordenar los datos y ubicar la posición central del conjunto, no la encontré.
Y luego, no sabía entre cuál número de datos dividir para calcular la media aritmética porque un día no tuve clases.
César pide ayuda para determinar entre el valor de la mediana y la media aritmética cuál es más representativo del tiempo que dedica a sus actividades de estudio y del tiempo que dedica a otras actividades y mostrar a sus papás que no tienen de qué preocuparse.
César manifiesta un par de dificultades que quizá también tengan otros compañeros y compañeras, pero justamente vamos a analizar con detenimiento la situación que presenta para apoyarle.
Es importante iniciar organizando los datos que César ha registrado y para eso debes elaborar una tabla de frecuencias.

Ahora registrar los datos. Comienza con el 0, porque es el menor valor de todos, solo hay uno y anota en frecuencia 1
Luego, revisa la tabla que envío César. Observa que hay dos cuatros, anotalos y así continua con el par de 5 que hay registrados.
Observa que César registró 6 horas cuatro veces y solamente una vez anotó 8 horas.
En total son los diez datos registrados.
Así es hay diez registros, la frecuencia total es 10
Ya puedes identificar el valor de la moda de este conjunto de datos, es 6
Efectivamente, es el valor de los datos con mayor frecuencia, es decir, es el número de horas dedicas a actividades escolares que más veces Cesar registró.
Recuerda que César no puede determinar la mediana del conjunto de datos. ¿Por qué crees que es?
Porque hay que encontrar la posición central a partir de la que queda dividido el conjunto de datos en dos partes iguales y aquí no queda ninguna posición central. Si consideró la quinta posición quedan cuatro datos antes de ella y cinco datos después. Si considera a la sexta posición, sucede lo contrario, hay 5 datos antes y cuatro después.
Esta situación ocurre cuando el número total de datos es un número par, como este conjunto que tiene 10 datos, es un número par de datos. ¿Y qué hacemos en ese caso?
En ese caso consideramos los valores de las dos posiciones que quedan en el centro, en este caso, los valores de la quinta y la sexta, y sacamos la media aritmética de ambos valores, ese será el valor de la mediana del conjunto de datos, es decir, consideramos a 5 y 6
Mira que coincidencia, tienen el mismo valor que las posiciones, pero no te confundas, debes obtener la media aritmética de los valores que ocupan la quinta y sexta posición, esto es, la media aritmética de 5 y 6
Es cinco más seis entre dos, da cinco con cinco décimos.
Con este cálculo obtienes el valor de la mediana, que en este caso, se ubica entre el valor del 5 y el 6
Y si contamos los datos que quedan antes de 5.5 y después de él, observamos que son 5 en ambos casos, por lo tanto, 5.5 divide a este conjunto en dos partes iguales.
Entonces debemos identificar cuántos datos forman el conjunto para saber de qué manera calcular el valor de la mediana.
Así es, cuando es un conjunto con impar número de datos, solo se identifica a la posición central y ese es el valor de la mediana.
Cuando es un conjunto con un número par de datos, se calcula la media aritmética de los valores de las dos posiciones que quedan al centro.
Debes considerar esto como una característica que tiene la obtención de la mediana de un conjunto de datos.
Con esto hemos atendido la primera dificultad de César. Vamos con la segunda, la que tiene que ver con la media aritmética. Vamos a ver cuál es su dificultad.
Recuerda que pide saber cuál es el número entre el que debe dividir la suma de los datos, si un día no tuvo clase. En este caso, entendemos que se refiere al día que anotó 0 horas, como el día que no tuvo actividad escolar, sin embargo, ese día lo contabilizó dentro de los días que hizo los registros, entonces, a la suma total de los datos, la debemos dividir entre 10 aunque un día tenga el valor de 0
Eso significa que, si se suma, 0+4+4+5+5+6+6+6+6+8, da 50 y eso lo debes dividir entre 10, con lo que obtienes 5 entonces ese es el valor de la media aritmética.
Ya conocemos los valores de las tres medidas que pueden representar a este conjunto de 10 datos.
El conjunto tiene el valor de 6 horas en actividades escolares como el de mayor frecuencia; 5.5 horas como el valor de la mediana y el valor de la media aritmética es 5 es decir, en promedio 5 horas diarias realiza actividades escolares.
Sin duda alguna, observa que regularmente nos referimos a la media aritmética como el promedio pero las tres medidas de tendencia central: moda, media aritmética y mediana, son valores promedio porque nos indican un valor central que es representante de un conjunto de datos.
Ahora, cómo podemos saber cuál es el más representativo, eso depende de analizar los datos y los valores de las medidas, así como del contexto o la situación a la que estamos haciendo referencia. En el caso de César, para poder recomendarle cuál de los tres valores es más representativo, necesitamos conocer también los valores de las medidas de tendencia central del conjunto de datos que corresponden a las horas que dedica a actividades no escolares. Vamos a calcularlos.

A partir de la tabla que Cesar envío, debes integrar una tabla de datos y frecuencias.

Esta tabla organiza y ordena debidamente los datos, vamos a verificar. Observa que el valor de la media aritmética es 5 horas promedio dedicadas a actividades no escolares y es igual al valor de la media aritmética del otro conjunto. Esto es, 5 horas en promedio dedicadas a actividades escolares. Tiene el mismo valor de media aritmética, entonces ocupa el mismo tiempo en promedio para cada tipo de actividad, ¿no? según el promedio, sí, pero veamos los valores de la mediana, ahí sí son muy diferentes, en una es 5.5 y en otra es 3 en ese caso, César podría usar como argumento ante sus papás que pasa en promedio 5.5 horas al día dedicadas a actividades escolares y 3 horas diarias no las dedica a actividades escolares.

Ahora veamos unas notas que enviaron algunos estudiantes sobre las calificaciones que obtuvieron en el primer trimestre, presta atención para saber cómo ayudar a Karla.
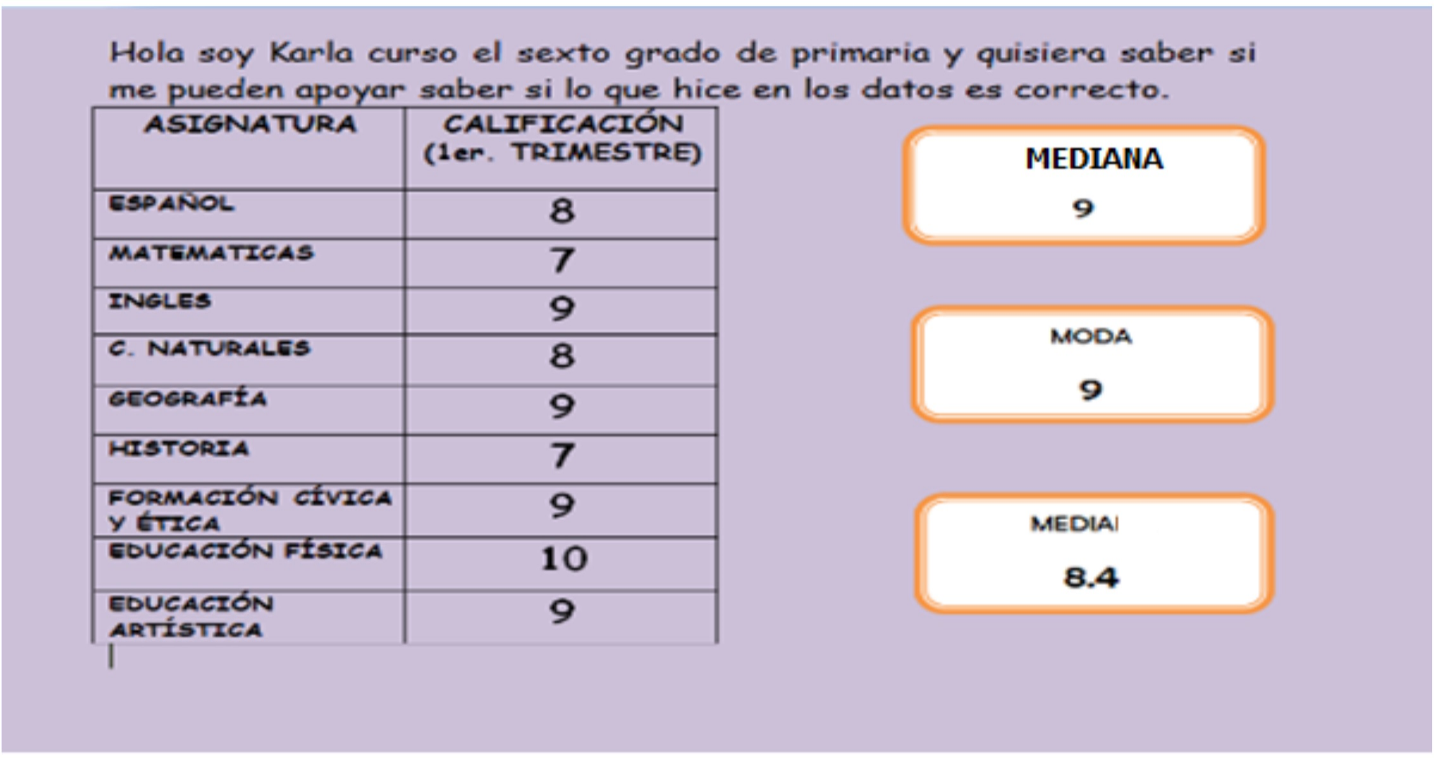
Ayuda a analizar lo que Karla envía y ve si es correcto, por supuesto, empieza por ordenar los números de menor a mayor, los datos quedarían de la manera siguiente:
7 7 8 8 9 9 9 9 10
Ahora es momento de analizar si está en lo correcto en lo de media, moda y la mediana.
El valor de su mediana es:
| Posición | 1° | 2° | 3° | 4° | 5° | 6° | 7° | 8° | 9° |
| 7 | 7 | 8 | 8 | 9 | 9 | 9 | 9 | 10 |
Su moda es:
| 7 | 7 | 8 | 8 | 9 | 9 | 9 | 9 | 10 |
Su media aritmética es:
7 + 7 + 8 + 8 + 9 + 9 + 9 + 9 + 10 = 76 ÷ 9 = 8.44
¡Los resultados de Karla son correctos!
Ahora es momento de empezar con el reto que está señalado en tu libro de texto, desafío 53, páginas 105 y 106
 |
 |
https://libros.conaliteg.gob.mx/P6DMA.htm?#page/105
Realiza las actividades.
Actividad 1
Para un estudio socioeconómico se aplicó una encuesta a 12 familias acerca del número de hijos que tienen y de su consumo semanal de leche.

Son doce familias y menciona que la familia 1 tiene 2 hijos, la familia 2 tiene 4 hijos, la familia 3 tiene 4 hijos, la familia 4 tiene 1 hijo, la familia 5 tiene 10 hijos, la familia 6 tiene 5 hijos, la familia 7 tiene 2 hijos, la familia 8 tiene 3 hijos, la familia 9 tiene 2 hijos, la familia 10 tiene 3 hijos, la familia 11 tiene 12 hijos y la familia 12 tiene 2 hijos. ¿Cuál es la mediana?
Ahora es momento de poner en práctica lo que se ha estado trabajando, ¿Ya sabes que hacer? Primero debes de ordenar los datos de menor a mayor, o de mayor a menor para poder llegar a la respuesta.
| 1 | 2 | 2 | 2 | 2 | 3 | 3 | 4 | 4 | 5 | 10 | 12 |
Lo primero que debemos de hacer para encontrar la mediana, ya con los datos ordenados. Observa que hay 12 datos y al ordenar las posiciones que quedan en el centro son la sexta y la séptima. En este caso, ¿Cómo puedes obtener la mediana? Recuerda que cuando tenemos estos casos, donde es par el número de datos, entonces, se suman los dos valores centrales y se dividen entre dos y eso queda de la manera siguiente.
| 1 | 2 | 2 | 2 | 2 | 3 | 3 | 4 | 4 | 5 | 10 | 12 |
3 + 3 = 6 / 2 = 3
Esto significa que la mediana es 3. La otra interrogante, ¿Cuál es la media aritmética o promedio del número de hijos? ¿Qué debes hacer? Debes realizar la suma de dichas cantidades, quedaría de la manera siguiente:
1+ 2 + 2 + 2 + 2 + 3 + 3 + 4 + 4 + 5 + 10 + 12 = 50
Ahora es tiempo de dividir el total entre 12 que es el número de familias de la encuesta aplicada y queda de la manera siguiente:
1+ 2 + 2 + 2 + 2 + 3 + 3 + 4 + 4 + 5 + 10 + 12 = 50 ÷ 12 = 4.1
Esta explicación servirá para la interrogante que está en el inciso b ¿Cuál es la media aritmética o promedio del número de hijos?
Ahora el inciso c) ¿Cuál de las dos medidas anteriores es más representativa de estas familias? y ¿Por qué?
Todas son medidas de tendencia central, la moda lo que más se repite, la mediana el dato o el promedio de los datos que ordenados todos por su valor, están en medio, pero recuerda que es muy común el uso de la media aritmética y se conoce como el promedio de todos los datos.
Tiene la característica que cuando hay valores muy pequeños, como el cero de la primera actividad o muy grandes, como 12 horas en actividades no escolares, su valor es afectado, en ese caso conviene más usar el valor de la mediana como el más representativo.
Actividad 2
Aquí hay que leer la información de la tabla B sobre el consumo semanal de leche y responder las preguntas.

Son doce familias y menciona que la familia 1 consumió 5 litros de leche, la familia 2 consumió 8 litros de leche, la familia 3 consumió 8 litros de leche, la familia 4 consumió 3 litros de leche, la familia consumió 15 litros de leche, la familia 6 consumió 10 litros de leche, la familia 7 consumió 3 litros de leche, la familia 8 consumió 6 litros de leche, la familia 9 consumió 3 litros de leche, la familia 10 consumió 7 litros de leche, la familia 11 consumió 28 litros de leche y la familia 12 consumió 3 litros de leche.
La interrogante del inciso a es, ¿Cuál es la mediana en el consumo semanal de leche de estas familias? Primero debes ordenar los datos de menor a mayor, quedan de la manera siguiente:
| 3 | 3 | 3 | 3 | 5 | 6 | 7 | 8 | 8 | 10 | 15 | 28 |
La interrogante dice, ¿Cuál es la mediana en el consumo semanal de leche de estas familias? ¿Cómo quedaría la respuesta?
Es momento de prestar atención y reafirmar lo aprendido, una vez que se tiene el registro de los datos se debe de observar y contar con lo que se solicita en la interrogante. La mediana en el consumo semanal de leche de estas familias, ¿Cómo quedaría la respuesta?
| 3 | 3 | 3 | 3 | 5 | 6 | 7 | 8 | 8 | 10 | 15 | 28 |
6 + 7 = 13 ÷ 2 = 6.5
La mediana es 6.5 litros de leche.
Ahora la pregunta del inciso b. El valor de la mediana, ¿Forma parte del conjunto de datos? Por supuesto que no siempre es uno de los valores de los datos, eso ocurre con la mediana de conjunto de número par de datos.
El reto de hoy:
Tu reto consiste en continuar aprendiendo y sobre todo en ponerte tu mismo retos que te permitan favorecer tus conocimientos y habilidades.
Debes de seguir las indicaciones, no olvides comentar lo que aprendiste en este tema, y sobre todo explica cómo pudiste resolver dicho desafío, una vez contestado el desafío, puedes compartir tus respuestas. Socializa tu conocimiento, recuerda que es una manera divertida el aprender, y sobre todo que el aprendizaje se construye entre todos.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas






Login to join the discussion