Lotería al revés
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:27Lotería al revés
Aprendizaje esperado: desarrollo de estrategias para el cálculo rápido de los productos de dígitos necesarios al resolver problemas u operaciones.
Énfasis: usar el cálculo mental para encontrar varias multiplicaciones que dan un mismo resultado. (1/2)
¿Qué vamos a aprender?
Todos estamos en espera de que los científicos logren la vacuna que proteja y permita volver a las actividades habituales. ¿Sabes que hay varios países en los que se trabaja para obtener esa vacuna? Donde han avanzado más es en China, Rusia, Estados Unidos e Inglaterra. De tener éxito podrían comenzar a comercializarla, es decir venderla a otros países, entre ellos México. En cada país se utilizan procesos de investigación diferentes, pero el fin es el mismo, obtener una vacuna que nos proteja contra el COVID-19.
De la misma forma que hay muchos procesos que llevan a obtener el mismo resultado en esto de las vacunas, en matemáticas, hay muchos caminos que nos llevan a un mismo resultado.
Seguirás analizando operaciones con las multiplicaciones y verás con cuáles obtienes el mismo resultado.
Para saber más sobre el tema explora los libros que tengas en casa o en Internet.
¿Qué hacemos?
¿Qué te pareció la relación que se hizo de las vacunas con las multiplicaciones?, hay diferentes caminos que te pueden llevar a un mismo lugar, en este caso a un mismo resultado.
Aprenderás con “La lotería de multiplicaciones”, pero con algunos cambios, se pude decir que ahora es al revés.
¿Cómo será? Observa muy bien cómo se juega y después tú puedas jugarlo en casa con algún miembro de tu familia.
En lugar de registrar las multiplicaciones en las cartas, se pondrán los resultados o productos y en las planillas de lotería, se registrarán las diferentes multiplicaciones que dan un mismo resultado.
Con el resultado que sale en las cartas, se marca en la planilla todas las multiplicaciones con las que se obtiene ese resultado y al llenar la planilla se gritará ¡lotería!,
Este juego se realiza entre varios participantes, pero si no pueden acompañarte a jugarlo puedes hacerlo tú solo, ¿Qué te parece que uses sólo una planilla para jugarlo?
- Participante 1 (P1) toma las tarjetas y dice el resultado y el participante 2, busca en la planilla todas las multiplicaciones que dan ese resultado.
En las multiplicaciones, los dos números que se multiplican se llaman factores y el resultado se llama producto. - Se tienen 15 multiplicaciones y en las tarjetas hay 8 resultados o productos.
| 6 x 3 | 1 x 9 | 2 x 4 |
| 1 x 8 | 2 x 9 | 2 x 1 |
| 4 x 2 | 3 x 3 | 7 x 1 |
| 3 x 6 | 9 x 1 | 1 x 1 |
| 8 x 3 | 1 x 7 | 9 x 2 |
P1: Saco la primera tarjeta y tiene el número 25.
P2: Busca, busca y no encuentra, no hay ninguna multiplicación que dé 25.
Ninguna multiplicación de la tarjeta tiene factores que al multiplicarse den 25.
P1: La segunda tarjeta es el número 2, ¿En alguna casilla hay dos números que multiplicados nos den 2?
P2: Busca, hay una, 2x1.
Hay dos casillas que tienen factores que al multiplicarse dan 2, 2x1 y 1x2.
P1: La siguiente tarjeta tiene el número 9, ¿En alguna casilla están dos números que al multiplicarse den como resultado el número 9?
P2: Busca, tengo una, 1x9, otra, 3x3 y la última 9x1.
Hay tres casillas que tienen factores que al multiplicarse dan 9, 1x9, 3x3 y 9x1.
P1: Toma la cuarta tarjeta y tiene el número 15, ¿En alguna casilla hay dos números que multiplicados den como resultado el número 15?
P2: Busca, busca y no hay ninguna multiplicación que de 15.
Efectivamente, no hay ninguna multiplicación que dé como resultado 15.
P1: La quinta tarjeta tiene el número 36, ¿En alguna casilla hay dos números que multiplicados den el número 36?
P2: Busca, busca y no hay.
¿De acuerdo? No hay factores que multiplicados den 36.
P1: La sexta tarjeta tiene el número 18, ¿En alguna casilla hay dos números que multiplicados nos den el número 18?
P2: Busca, 6x3, 2x9, 3x6, 9x2. Fueron 4 casillas.
Hay 4 multiplicaciones cuyo producto es 18.
P1: La séptima tarjeta tiene el número 12, ¿Hay alguna casilla en donde se encuentren dos números que multiplicados den el número 12?
P2: Busca, busca y no hay.
No hay factores que multiplicados den 12.
P1: Saca la última tarjeta que tiene el número… 8, ¿Hay casillas en donde se encuentren dos números que multiplicados den como resultado 8?
P2: Busca y encuentra 2x4, 1x8 y 4x2…
¿Qué tal te pareció esta dinámica para aprender a multiplicar?
Algo interesante de esta actividad es que había multiplicaciones que eran inversas y daban el mismo resultado como 2 x 4 y 4 x 2.
Esto te ayuda a recordar más fácilmente el resultado de estas multiplicaciones.
También, algo que parece muy sencillo es que todos los números que se multiplican por 1, tienen como resultado el mismo número.
¿Y te fijaste si hay algún número que sólo se pueda representar con una multiplicación?
El 1, ya que su única multiplicación es 1x1 y al revés es igual, por lo que sólo cuenta una vez. Eso mismo sucede con todos los números que se multiplican por sí mismos. Sólo los puedes obtener con una sola multiplicación.
Recuerdas tu cuadro de multiplicaciones, pues ahí puedes darte cuenta de varias cosas. Por ejemplo, si regresas al juego de la lotería, al sacar la tarjeta del 8, rápidamente buscas su mitad y así se sabe que se debe de multiplicar por 2. La mitad de 8 es 4, entonces, si multiplicas el 4 por 2 da el 8 otra vez… Y pasa lo mismo con otros, por ejemplo, con el 18, la mitad es 9 y luego se multiplica por 2 y regresa al 18.
Los números a los que les sacas la mitad y luego esa mitad se multiplica por 2, regresa al número inicial, es bueno retomar la tablita para recordar las multiplicaciones.
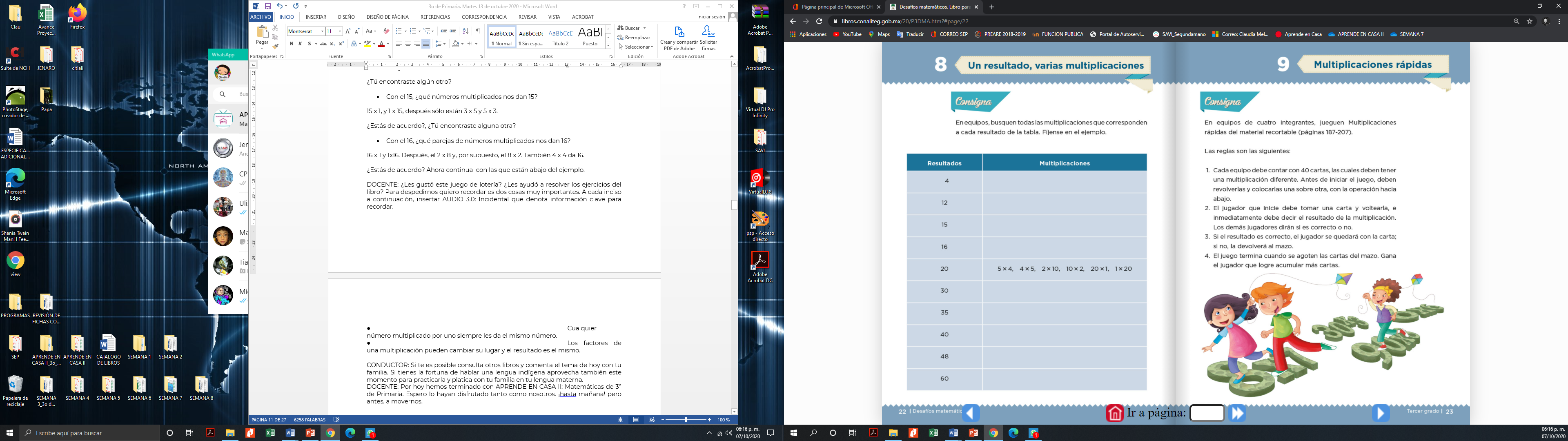
Ahora, resuelve un desafío de la página 22 de tu libro de Desafíos Matemáticos.
https://libros.conaliteg.gob.mx/20/P3DMA.htm?#page/22
Como puedes observar, aquí también multiplicarás para un mismo resultado o producto. Aquí el resultado está escrito y te pide escribir todas las multiplicaciones que den ese producto o resultado.
Te parece bien si vas encontrando las multiplicaciones para los resultados que te dan, ve anotándolos en la tabla.
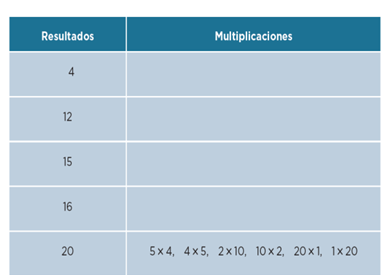
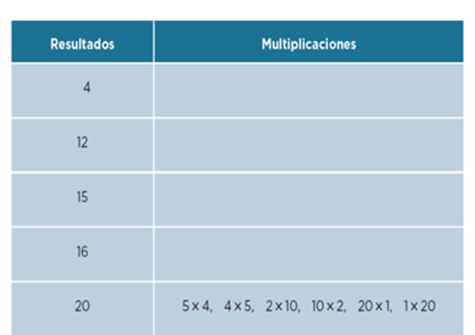
Primero observa el ejemplo que te dan en el libro.
El resultado es 20. ¿Qué parejas de números multiplicados te dan 20? Verifica si no faltó alguna… 5 x 4 es igual a 20 y el también 4 x 5; luego 2 x 10 son 20 y, por supuesto, 10 x 2; finalmente 20 x 1 y claro, 1 x 20. Bien, sí están todas. Ahora anota, las de los otros renglones.
Observa el cuadro:
Con el 4, ¿qué parejas de números multiplicados dan 4?
4 x 1 y al revés 1 x 4, porque son los mismos factores, sólo que cambiaron de lugar. Otro es 2 x 2, porque sacas mitad al 4 y ese número multiplicarlo por 2 y como al revés es el mismo sólo cuenta una vez. Se encontraron tres multiplicaciones.

Sigue el 12, ¿qué parejas de números multiplicados dan 12?
12x1, y al revés, 1x12; luego 6 x 2 y al revés 2 x 6; después sé que en la tabla del 3 hay un 12, es 3 x 4 y también al contrario 4 x 3.

¿Tú encontraste algún otro?
Con el 15, ¿qué números multiplicados dan 15?
15 x 1, y 1 x 15, después sólo están 3 x 5 y 5 x 3.

¿Tú encontraste alguna otra?
Con el 16, ¿qué parejas de números multiplicados dan 16?
16 x 1 y 1x16. Después, el 2 x 8 y, por supuesto, el 8 x 2. También 4 x 4 da 16.

¿Estás de acuerdo? Ahora continúa con las que están abajo del ejemplo.
https://libros.conaliteg.gob.mx/20/P3DMA.htm?#page/22
¿Te gustó este juego de lotería?
Y el ejercicio de la pág. 22 de tu libro, solo practicando puedes memorizar las multiplicaciones.
Recuerda:

Platica con tu familia lo que aprendiste, seguro les parecerá interesante y podrán jugar contigo y aprender a memorizar las multiplicaciones.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:





Login to join the discussion