Losetas cuadradas
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:57Aprendizaje esperado: determina divisores o múltiplos comunes a varios números. Identifica, en casos sencillos, el mínimo común múltiplo y el máximo común divisor.
Énfasis: resuelve problemas que implican determinar divisores comunes de dos o tres números.
¿Qué vamos a aprender?
Determinarás divisores o múltiplos comunes a varios números; identificarás, en casos sencillos, el mínimo común múltiplo y el máximo común divisor; y resolverás problemas que impliquen determinar divisores comunes de dos o tres números.
¿Qué hacemos?
Continúa analizando situaciones que están relacionadas con múltiplos, particularmente, con múltiplos comunes de dos o más números. Recuerda que ya has trabajado este contenido de múltiplos, por ejemplo, en algunos temas posteriores a esa sesión donde relacionaste varios contenidos matemáticos con el uso de los múltiplos de los números, como el cálculo del volumen o en la proporcionalidad.
En algunas de las tablas que completaste había valores que eran múltiplos de otros, recuerda rápidamente algunas características de los múltiplos de algunos números que ya estudiaste.
Relaciona los textos de ambas columnas.
|
Preguntas: 1.- ¿Cuál es una de las características de los múltiplos de 2? ( ) 2.-¿Cuáles son las características de los múltiplos de 5? ( ) 3.-¿Cuáles son las características de los múltiplos de 10? ( )
|
Respuestas:
c) Todos son números pares. |
Verifica tus respuestas.
Es 1 con c, es decir, la característica de los múltiplos de dos es que todos son números pares, efectivamente 2, 4, 6, 8, 10, 12, 14, 16, 18 y todos los demás múltiplos de dos, son números pares, es decir, terminan en cero, dos, cuatro, seis u ocho.
La pregunta 2 va con la respuesta del inciso a) porque los múltiplos de 5 son números que terminan en 0 y 5
Finalmente, la pregunta 3 va con el inciso b) porque todos los múltiplos de 10 son los números que terminan en cero.

Este solo fue un ejercicio para recordar algo sobre el tema de los múltiplos de un número. Ahora ya puedes avanzar más rápido en la sesión, por eso es importante llevar la secuencia de tu trabajo.
Para continuar observa la siguiente tabla sobre un juego de números y de multiplicaciones. Es la historia de las tres hermanas y la venta de las manzanas del huerto de su papá.
Observa con atención la información que muestra una de las tablas que se hicieron para resolver el problema, la cual te permitirá comprender mejor la situación. Vas a fijarte en las columnas centrales que ahora están marcadas con una flecha, ¿Ya las identificaste?
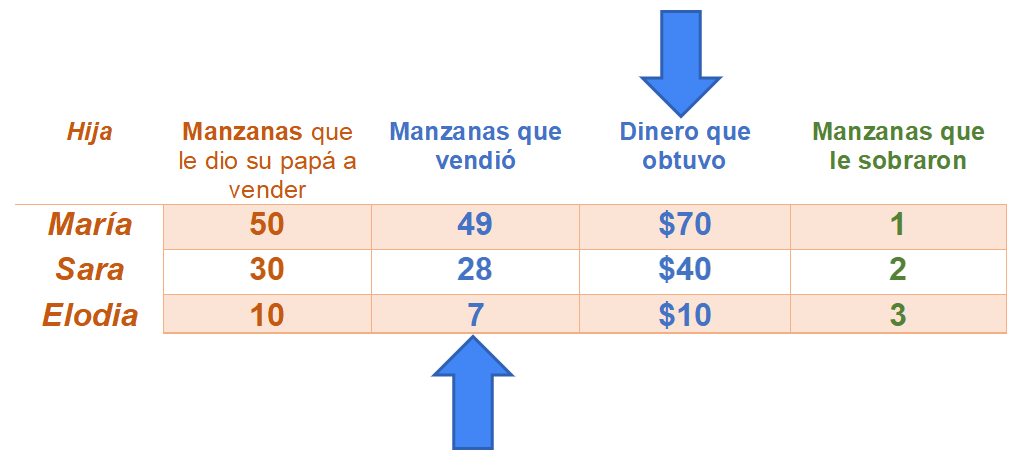
Responde a la pregunta, ¿Qué tienen en común los números que acabas de ver? Parece que son los números de la tabla del 7
¿Estás en lo correcto? ¿Cómo lo puedes comprobar? Puedes buscar el número entero que multiplicado por 7 te da, 7 luego 28 y después haces lo mismo para el 49 así tienes que:
7 x 1 es 7;
4×7 es 28,
7 × 7 da como resultado 49

Exacto, es una manera de comprobar que el 7 el 28 y el 49 son múltiplos de 7 además, 10, 40 y 70 son respectivamente, las cantidades en pesos obtenidos en la primera venta de manzanas que cada hermana hizo y son múltiplos de 10 porque terminan en cero.
Aquí se está usando una de las características de los múltiplos de 10 esa descripción que hace referencia a la característica de los múltiplos de 10 es algo que conoces con el nombre de criterio de divisibilidad, esto es, que se puede decir que un número se puede dividir exactamente entre 10 si termina en cero.
Se dice que todo número que termina en cero se puede dividir exactamente entre 10
Ahora analiza otra situación. Tienes dos rectángulos. Observa los números que hay dentro de cada rectángulo. ¿A qué número corresponden los múltiplos del primer rectángulo?

Son los múltiplos de 2 hasta el 50
Los múltiplos del segundo recuadro, ¿A qué número corresponden? Son los múltiplos de 5 hasta el 50
Ahora, la actividad es cruzar los dos rectángulos, de tal manera que se destaque claramente cuáles son los múltiplos que tienen en común el 2 y el 5 es decir, los múltiplos de 5 que también son múltiplos de 2 y los múltiplos de 2 que también son múltiplos de 5 ¿Cuáles son los múltiplos comunes de 2 y 5?
Identifica a los múltiplos que aparecen en el recuadro de los múltiplos de 2 y que también aparecen en el recuadro de los múltiplos de 5
Piensa, ¿De qué manera puedes acomodar los números que hay en los rectángulos para mostrar cuáles sólo son múltiplos de 2 ¿Cuáles sólo son múltiplos de 5? y ¿Cuáles son múltiplos tanto de 2 como de 5?
Primero, verifica que ya tienes a los múltiplos comunes de 2 y 5 que aparecen en los dos rectángulos, después, acomoda los rectángulos de tal manera que queden empalmados de un lado y se genere el espacio suficiente para anotar los múltiplos que tienen en común el 2 y el 5, son: 10, 20, 30, 40 y 50
En cada recuadro anota los múltiplos de cada uno de los otros números.

¿Por qué crees que se les nombra múltiplos comunes?
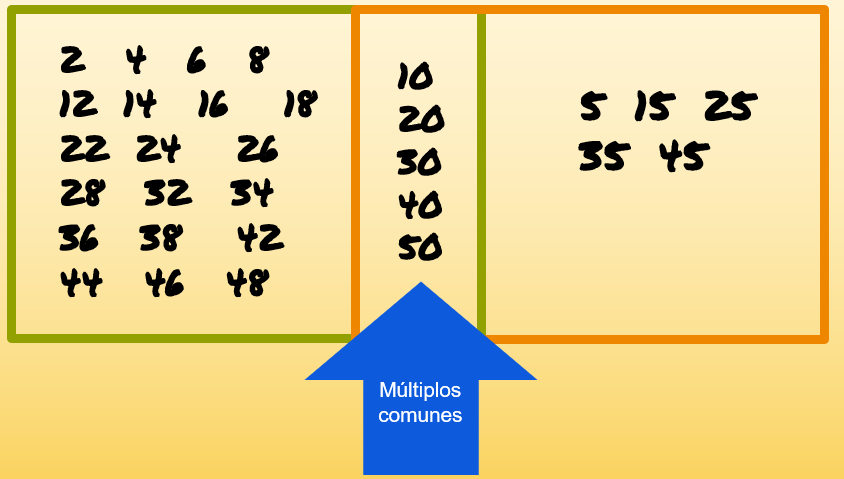
Se llaman múltiplos a los números que son el resultado de una multiplicación de dos números y comunes, porque son múltiplos de los dos números, es decir, se encuentran en los dos rectángulos, exactamente, en el ejemplo, son múltiplos comunes porque los encuentras como múltiplos de 2 y también como múltiplos de 5
Por eso es que 10 es un múltiplo común de 2 y de 5 porque aparece en los múltiplos de 2 pero también lo encuntras en los múltiplos de 5
Los múltiplos pueden ser comunes a dos, tres o más números. Como los que acabas de encontrar, por ejemplo: puedes encontrar que 30 es múltiplo de 2 y de 5 pero también es múltiplo de 3, 6, 10 y 15

Sí, porque cinco por seis es treinta como diez por tres o 15 por 2 en todos los casos el resultado es treinta.
Ahora es momento de que apliques tus conocimientos en el Desafío 74 llamado “Sin cortes”, que se encuentra el pagina 136 de tu libro de texto.
https://libros.conaliteg.gob.mx/P6DMA.htm?#page/136

La consigna 1, problema 1 con su primer inciso dice lo siguiente:
En equipos resuelvan los siguientes problemas:
-
Se requiere cubrir un piso rectangular de 450 cm por 360 cm con losetas cuadradas de igual medida, no se vale hacer cortes, es decir el número de losetas tendrá que ser un número entero.
Inciso a. Escriban tres medidas que pueden tener las losetas para cubrir todo el piso.
¿Se te ocurre alguna forma en que se pueda resolver esto? ¿Cómo crees que puedes encontrar las medidas de la loseta? Tal vez se te ocurre que una opción puede ser hacer líneas en el piso, que formen recuadros y después medirás el tamaño de lo que quedó, si es así, necesitarás un espacio mucho muy grande.
Primero debes analizar más la información que te brinda el problema para cubrir con losetas un piso de forma rectangular que mide 450 cm por 360 cm. No olvides que puedes visualizar en tu mente el rectángulo o también hacer un dibujo para representarlo.

Así es, imagina un piso de forma rectangular, en el cual tienes dos dimensiones: largo 450 cm y ancho 360 cm. Imagina las líneas que propones para trazar cuadros en ese piso, algo así como hacer una retícula.
Los cuadros son las losetas, y las losetas cuadradas las venden de diferentes tamaños, así es, para cubrir un piso con las medidas señalada específicamente y sin que sobren ni se corten piezas, ¿Cuáles serían las opciones con respecto al tamaño de las losetas de forma cuadrada que puedes comprar?
Imagina que el rectángulo es el piso y aquí tienes las medidas de sus dos dimensiones, largo y ancho. Recuerda que los múltiplos de 10 terminan en 0 y date cuenta de que el 450 y el 360 terminan en 0
También imagina colocar losetas cuadradas para cubrir el largo del piso y luego colocar otra franja de losetas para cubrir el ancho.

Para cubrir el largo necesitas 45 losetas cuadradas de 10 cm por lado y, para cubrir el ancho, requieres de 36 losetas, entonces las losetas cuadradas que uses serán de 10 cm de largo y 10 cm de ancho, es decir, 10 por 10
Así es porque, si multiplicas 10 cm de lado que tiene cada loseta por 45 losetas, es igual a 450 cm. Esto te da la medida exacta del largo del piso que vas a cubrir y si multiplicas 36 losetas por 10 cm, tienes 360 cm, que corresponde a la medida de ancho del piso, de esta forma compruebas que los cálculos son correctos.
También puedes intentar con otra medida para las losetas, recuerda que las dimensiones del piso son de largo 450 cm y 360 cm de ancho.
Pensando en que la primera loseta cuadrada mide 10 cm en cada una de sus dimensiones, podrías usar losetas cuadradas de 20 cm por lado, de este modo, al largo le faltarían 10 cm, entonces, no te sirve esta medida de loseta.
¿Qué te parece si continuas con tu estrategia y lo intentas con una loseta cuadrada de 30 cm por lado? Losetas de 30 cm por lado. Si ocupas 10 losetas serían cubiertos 300 cm por largo y si agregas dos losetas más cubrirías 60 cm más; así ya tienes cubierto el ancho del piso, es decir, 360 cm.
De esa manera ocuparías 12 losetas cuadradas para cubrir los 360 cm de ancho del piso. Ahora analiza si ese tamaño de loseta cuadrada te sirve para cubrir el largo del piso.
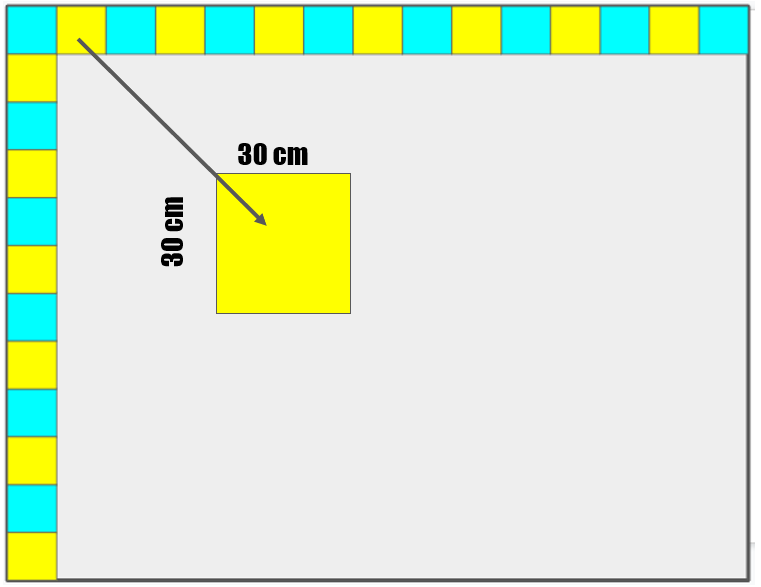
10 losetas cuadradas de 30 cm por lado te permiten cubrir 300 cm de largo, y 5 losetas cubren 150 cm, entonces necesitarías 15 losetas cuadradas de 30 cm por lado para cubrir el largo del piso.
Exacto se requieren 15 losetas cuadradas de 30 cm por lado para cubrir el largo del piso sin que sobre ni falten losetas, por lo tanto, como puedes observar en la imagen, con esas dimensiones se pueden colocar 15 losetas cuadradas para cubrir el largo y 12 losetas para el ancho, 15 por 12 es igual a 180 losetas cuadradas de 30 cm por lado que se requieren para cubrir los 162 000 centímetros cuadrados del piso, ya que mide 450 cm de largo por 360 cm de ancho.
Aquí haz aplicado el concepto de múltiplos comunes. ¿En qué te diste cuenta de eso?

45 por 10 es igual a 450 por lo tanto, 450 es un múltiplo de 45 y 10 pero también lo es de 30 y 15 porque 15 por 30 son 450 entonces 450 es múltiplo común de 45, 10, 15 y 30
El reto de hoy:
Comparte los ejercicios que hiciste con algún familiar cercano y explícale como que obtuviste tales resultados.
Si te es posible, consulta otros libros o materiales para saber más sobre el tema.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas

https://libros.conaliteg.gob.mx/20/P6DMA.htm











Login to join the discussion