Los asientos del teatro
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:27
Aprendizaje esperado : r esolución de multiplicaciones cuyo producto sea hasta del orden de las centenas, mediante diversos procedimientos (como suma de multiplicaciones parciales, multiplicaciones por 10, 20, 30, etcétera).
Énfasis: u tilizar la descomposición de números para resolver problemas que impliquen multiplicar números de dos cifras.
¿Qué vamos a aprender?
Resolverás multiplicaciones cuyo producto será hasta las centenas, mediante varios procedimientos.
Esperamos que esté s con mucho entusiasmo por continuar t us clases después de su descanso de fin de año.
Recuerda que aún continúa la emergencia sanitaria por el COVID-19. Muchas de las actividades cotidianas se encuentran con algunas restricciones y ustedes deben seguir cuidándose para no enfermar.
E l domingo pasado fui al teatro con mis sobrinos y sólo permiten un aforo de una tercera parte del cupo total.
U n aforo de u na tercera parte del cupo total, q uiere decir que no se venden todos los boletos del teatro, sólo se venden poco menos de una tercera parte de los asientos, con el fin de que haya una sana d istancia entre los asistentes, a demás de que al entrar se siguen todas las medidas sanitarias para evitar contagios.

D entro de esas medidas está que no puede haber público en la primera fila, ya que es la que se encuentra más cerca de los actores.
Lo que nos podemos preguntar es , ¿C ómo hacen para contar todos los asientos que hay en el teatro de manera rápida?
Los cuentan por secciones y así es más fácil.

Qué t e parece si checas en in ternet las secciones que tiene un teatro y calcula s el número de asientos.

¿Qué hacemos?
Ya t enemos aquí los datos. Es un mapa que muestra las secciones y lugares que tiene el teatro.
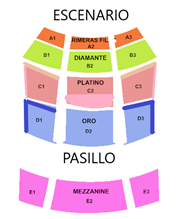
Te parece que primero los organicemos en una tabla para facilitar el trabajo.
Ve haciendo este trabaj o en t u cuaderno.
L a tabla puede tener una columna donde anot emos las secciones del teatro, o tra columna donde anotemos el número de filas, una más con el número de asientos por fila y al final podemos anotar cuántos asientos hay por sección.
|
TEATRO ILUSIÓN |
|||
|
Sección |
No. de filas |
Asientos por fila |
Asientos por sección |
|
A |
18 |
12 |
216 |
|
B |
11 |
42 |
462 |
|
C |
14 |
25 |
350 |
|
D |
20 |
18 |
360 |
|
E |
10 |
30 |
300 |
|
Total de filas: 73
|
|||
|
Total de asientos del teatro: 1688
|
|||
También vamos a anotar el total de filas que tiene el teatro y hasta abajo el total de asientos .
A sí queda muy completa la información de la tabla. Bien, este teatro tiene 5 secciones que las identifican con letras: A, B, C, D, y E.
El número de filas en la sección A es 18 y cada fila tiene 12 asientos.
Ya están anotados, ¿Q ué podríamos hacer para saber cuánto s asientos tiene cada sección? c omencemos con la sección A.
Podríamos sumar 12, que es el número de asientos, 18 veces, que es el número de filas, pero eso es muy largo, mejor hacemos una m ultiplicación de 12 x 18 y son 216 .
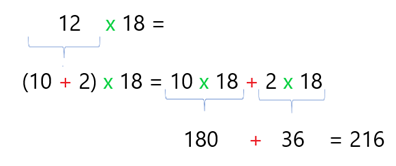
S e podrían sumar los 12 asientos de cada fila 18 veces, pero recordemos que sumar un mismo número varias veces equivale a realizar una multiplicación.
Ahora, hay que obtener el número de asientos de la sección B.
L a sección B tiene 11 filas con 42 asientos en cada fila. Ni modo de sumar once , 42 veces, es muy largo, mejor hagamos una multiplicación , entonces 11 x 42 o 4 2 x 11, me van a dar lo mismo, e ntonces descompuse el once en 10 más uno y los multipliqué por 42, lo que me dio en total 462 asientos en la sección B.
E s importante recordar te que da igual descomponer cualquiera de los dos factores.
En este caso se descompuso el 11, pero veamos qué resultado obtenemos al descomponer el 42.
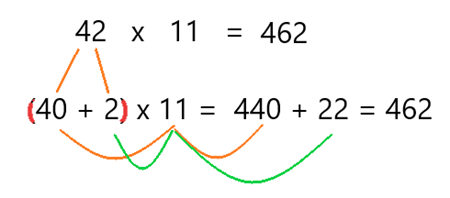
Una forma fácil de descomponerlo es 40 más 2 y estos dos números los multiplicamos por 11, al final sumamos sus resultados.
¿Y si el 42 lo descompongo como 10 + 10 + 10 + 10 + 2 y todos estos números los multiplico por 11, luego sumo sus resultados, me daría el mismo resultado anterior?
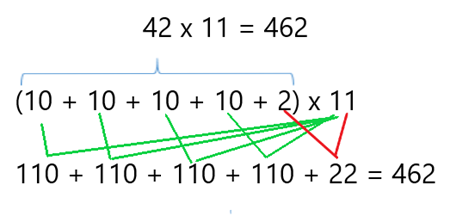
¿Qué crees , dará o no el mismo resultado? vamos a ver , 10 por 11 son 110 y 2 por 11 son 22, sumamos todos y nos da 462 también.
Pero es más sencillo si lo descomponemos sólo en dos sumandos, porque son más cortas las operaciones.
E l chiste de multiplicar es que ahorres tiempo usando un camino más corto. Bien, ahora pasemos a la sección C donde el número de filas es 14 y cada fila tiene 25 asientos.
O tra vez esto se resuelve con una multiplicación de 14 por 25, o bien, 25 por 14, para ahorrarnos tiempo y a mí se me ocurre que puedo descomponer el 14 en 10 más 4, porque me es muy fácil multiplicar por decenas. Entonces tengo 2 5 por 10 más 25 por 4, y me da 250 más 100 son 350.
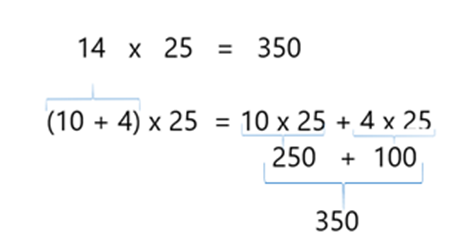
Tú , ¿E stá s haciendo las operaciones para saber el total de asientos por sección? ¿Estás obteniendo los m ismos resultados que nosotros? e spero que sí.
Pasemos ahora a la sección D.
En la sección D hay 20 filas y cada una tiene 18 asientos, por lo que voy a multiplicar 20 x 18. Yo voy a descomponer aditivamente el 18 y queda 10 + 8 y formo dos multiplicaciones, 20 x 10 y 20 x 8, las resuelvo, 20 x 10 = 200, 20 x 8 = 160 y sumo sus resultados, 200 + 1 60 = 360
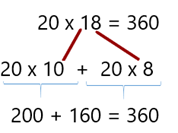
Pero no te acordaste que multiplicar por un número que termina en cero es igual a multiplicar la cifra diferente de cero de ese factor por el otro factor y luego al resultado aumentar los ceros que tenga el primero.
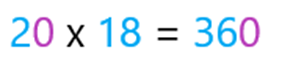
¡ E s verdad, se t e olvidó ese camino, y es más corto!
E se es el chiste de estudiar algo, que podamos usarlo cuando se nos presente la situación, p ero vamos con la última sección.
La sección E tiene 10 filas con 30 asientos cada una. Aquí ya recordé cómo se multiplican los números que terminan con ceros, así que multipliqué 1 x 3 que son 3 y aumenté el cero del diez y el cero del treinta, por lo tanto, el resultado es 300.
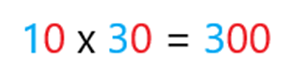
¿Estás de acuerdo? a hora ya sólo nos falta saber cuántas filas y cuántos asientos tienen el teatro.
P ara saber eso só lo tenemos que sumar y nos dan 73 filas. Ahora sumemos la cantidad de asientos por sección y nos da 1688 asientos que tiene el teatro.
|
TEATRO ILUSIÓN |
|||
|
Sección |
No. de filas |
Asientos por fila |
Asientos por sección |
|
A |
18 |
12 |
216 |
|
B |
11 |
42 |
462 |
|
C |
14 |
25 |
350 |
|
D |
20 |
18 |
360 |
|
E |
10 |
30 |
300 |
|
Total de filas: 73 |
|||
|
Total de asientos del teatro: 1688 |
|||
Ahora sólo falta que nos digas cuántas personas tiene permitido aceptar el teatro para una función.
Sólo le permiten aceptar una terce ra parte, que son en este caso 562 personas y como dije al principio, esto con el fin de que haya distancia entre ellas y disminuir el riesgo de contagio.
E so es lo mejor, a hora hagamos un juego de multiplicaciones.
Sacamos una tarjeta y cada uno hace la multiplicación que ahí está indicada, el primero que t enga el resultado dice: ¡alto! y los demás jugadores ya no pueden seguir escribiendo.
|
20 x 14 |
30 x 12 |
50 x 11 |
80 x 12 |
|
15 x 20 |
13 x 30 |
60 x 13 |
90 x 13 |
|
12 x 90 |
15 x 40 |
11 x 90 |
10 x 18 |
|
11 x 80 |
12 x 70 |
11 x 70 |
11 x 90 |
|
11 x 60 |
12 x 20 |
15 x 30 |
13 x 70 |
Si está bien el resultado se anota 100 puntos, si está incorrecto su resultado, se anota cero. Al terminar el juego sumamos y quien obtuvo más puntos, gana.
|
280 |
360 |
550 |
960 |
|
300 |
390 |
780 |
1170 |
|
1080 |
600 |
990 |
180 |
|
880 |
840 |
770 |
990 |
|
660 |
240 |
450 |
910 |
¿J ugamos?
Tú, también juega c on nosotros, al final, verifica si está bien t u resultado, para ver cuántos puntos hace s. ¿Lista/o con t u cuaderno?
Saca una tarjeta tú primero.
-
20 x 14
Realiza la operación, verifica el resultado en la parte posterior de la tarjeta.
Puedes hacer las rondas que quieras , a l final haces t ú conteo de puntos, para decidir quién fue el ganador.
¿ C ómo te fue con estas o peraciones? ¿Qué estrategia usaste para resolverlas? ¿Cuántos puntos hici ste ?
Rec uerda que para realizar multiplicaciones de números de dos cifras donde ninguno termina con ceros, se descompone aditivamente uno de ellos y se form an multiplicaciones conocidas, a l final se suman sus resultados.
También recuerd a que cuando se multiplica por números que terminan con ceros, pueden multiplicar las cifras que no son ceros y al resultado le aumentan los ceros que tengan al final los factores.
Si te es posible consulta otros libros y p latica con tu familia lo que aprendiste, seguro les parecerá interesante y podrán decirte algo más.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más :
Lecturas



Login to join the discussion