Leyes de cancelación
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:22Aprendizaje esperado: resuelve problemas que implican el uso de ecuaciones de segundo grado.
Énfasis: usar las leyes de cancelación al resolver ecuaciones.
¿Qué vamos a aprender?
Analizarás las leyes de cancelación en términos aritméticos y algebraicos.
Los materiales que vas a utilizar es tu cuaderno de apuntes, bolígrafo, lápiz y goma.
En Matemáticas, al simplificar expresiones numéricas o algebraicas, se usan leyes y propiedades que aplican a ciertas operaciones.
Al resolver algunos problemas, posiblemente has aplicado estas leyes sin darte cuenta. Cada una de ellas tiene su nombre y propiedades.
- Las propiedades del elemento neutro,
- Las leyes asociativas, conmutativas, y
- Las leyes de cancelación.
La propiedad del elemento neutro se aplica para la suma y resta, así como para la multiplicación y división.
¿Son diferentes para cada operación?
No propiamente, el elemento neutro de una operación es el número que, operado con cualquier otro número, no altera al número original , es decir, en el caso de la suma o resta, el número cero es el que no cambia el resultado al realizar la operación .
¿Qué hacemos?
Observa algunos casos numéricos y algebraicos para que quede clara la propiedad.
Por ejemplo:

En el caso de la multiplicación y la división, no se puede considerar al cero como elemento neutro, ya que, si partes del mismo principio que debe ser un número que no altere o modifique al original al momento de realizar la operación de multiplicación o división, este número ahora debe ser el uno.
Entonces, todo número o término multiplicado o dividido por uno permanece igual. Observa los siguientes ejemplos:
Si se multiplica: 459.58 por 1, el resultado es 459.58.
Tres décimos por 1, son tres décimos.
Si se divide 459.1 entre 1, el resultado es 459.1
Tres décimos entre 1, se obtiene tres décimos
5x^2 entre 1 es igual a 5x^2
Entonces existen dos elementos neutros, uno aditivo para la suma y resta, que es cero, y otro multiplicativo para la multiplicación y división, que es uno.
Continua con las leyes asociativa y conmutativa.
Pero ¿qué diferencia hay entre las leyes asociativa y conmutativa?
Se diferencian una de la otra en que la ley asociativa permite agrupar o asociar los sumandos o factores y se obtiene el mismo resultado y, en el caso de la ley conmutativa, se intercambian de lugar los sumandos o factores sin cambiar el resultado.
La ley asociativa se aplica en la suma o multiplicación, al agrupar o reagrupar los números, ya sean sumandos o factores, con paréntesis, por ejemplo:

Si se agrupan (12 + 56) + 44, es igual a sumar 68 + 44 con resultado 112.
Al cambiar la agrupación, se tiene 12 + (56 + 44), el resultado es 12 + 100, es decir, 112.
En el caso de la multiplicación, 4 por 10 por 5, se agrupan en 4 por 10 por 5, se tiene 40 por 5 y el resultado es 200.
Otra forma de agrupar es multiplicar 4 por la agrupación (10 por 5), que es igual a 4 por 50 y el resultado es igual a 200.
Es decir, los números se pueden agrupar o reagrupar, a sí como las personas pueden asociarse con otras personas en grupos diferentes.
Es importante resaltar que para la resta y división no se puede aplicar la ley asociativa, en estas operaciones sí importa cómo se agrupen las cantidades al realizar la operación.
La ley conmutativa sólo se puede aplicar en la suma y la multiplicación . Se cambia el orden de los sumandos o en la multiplicación los factores, ambos con el mismo resultado. Por ejemplo:
Si se divide 15 entre 3, su resultado es 5. Si se divide 3 entre 15, el resultado es 1/5.
Se muestran los siguientes ejemplos:
1. Se quiere sumar 28.48 + 100.12, el resultado es: 128.60. La ley conmutativa permite expresar la suma como 100.12 + 28.48 con el mismo resultado 128.60

2. Al multiplicar tres quintos por dos séptimos, el producto es seis treintaicincoavos. Se aplica la ley conmutativa al cambiar el orden de los factores: dos séptimos por tres quintos, cuyo resultado no se altera y es seis treintaicincoavos.

3. Con tres o más factores ocurre exactamente igual, por ejemplo: se multiplica 4x^2 por 10x^3 por 11x.
Al multiplicar 4x^2 por 11x y, el resultado 44x^3 se multiplica por 10x^3, dando 440x^6.
O bien, se multiplica 10x^3 por 11x y, el resultado 110x^4 se multiplica por 4x^2, se obtiene 440x^6.

Al aplicar la ley conmutativa y cambiar el orden de los sumandos y/o factores, no se altera la suma y/o producto. Lo cual facilita resolver las operaciones. No es posible aplicar esta ley en la resta o división, pues, al invertir el orden de las operaciones, cambia el resultado.
Un ejemplo de la ley conmutativa en la vida diaria es: invertir el orden de los pies al colocar los calcetines, es decir, no importa si primero se coloca el derecho o primero el izquierdo.
Pero si se intercambia el colocar primero los zapatos y luego los calcetines, en ese caso es importante el orden.
Ahora, analiza la ley de cancelación, primero para la suma y resta.
En una expresión numérica o algebraica se encuentra el mismo número o término realizando la misma operación de suma o resta en ambos lados de la igualdad, entonces se puede cancelar.
Para que esta ley de cancelación quede más clara, se muestran algunos ejemplos:
Los valores numéricos se representan con literales:

“a” más “x” es igual a “b” más “x”.
El término “x” está en ambos lados de la igualdad, aplicando la misma operación de suma.
Entonces, se cancela el término “x” en ambos lados de la igualdad y el resultado es “a” igual a “b”.
En el caso de la resta, es igual.
“a” menos “x” igual a “b” menos “x”, se cancela el término “x” en ambos lados de la igualdad, el resultado es “a” igual a “b”.
Esta ley de cancelación ayuda a simplificar procedimientos. Observa los dos casos.
Se tiene la siguiente igualdad:
(15 por 2) + 9 = 18 +12 + 9

En ambos miembros de la igualdad, el número 9 está sumando, se aplica la ley de cancelación para eliminar el número 9, se obtiene 15 por 2 = 18 + 12.
Las operaciones de cada miembro, 15 por 2 es 30 y 18 más 12 es 30.
30 igual a 30. Se mantiene la igualdad.
¿Ocurre lo mismo si son términos algebraicos? Para responder se analiza la siguiente igualdad.
10n + 14n – 35m + 8 = 4 por 2 – 35m + 24n

Se observa que en ambos miembros de la igualdad se resta 35m. Se aplica la ley de cancelación y se elimina 35m en ambos términos, el resultado es: 10n + 14n + 8 = 4 por 2 + 24n
Se opera en ambos miembros:
En el primer miembro se suman 10n + 14n, por ser términos semejantes, se obtiene 24n y el número 8 se escribe igual.
En el segundo miembro se realiza el producto de 4 por 2, se obtiene 8 y se repite 24n.
Al final, se tiene: 24n + 8 = 8 + 24n.
En el resultado anterior se observa que no está escrito de la misma forma en la igualdad, se aplica la ley conmutativa y representan lo mismo.
En la siguiente ecuación lineal se puede observar lo útil que es la ley de cancelación.
“x” más 2 por “x” menos 5 igual a, 2x menos 10 más 4

Al operar, se escribe la “x” más el resultado de multiplicar 2 por “x” menos 5.
Dos por “x” es 2x, dos por 5 negativo es 10 negativo. En el segundo miembro, se escribe igual 2x menos 10 más 4.
No se agrupan los términos porque se repiten en ambos miembros de la igualdad.
Se aplica la ley de cancelación para eliminar de ambos lados de la igualdad los términos “2x menos 10”, el resultado es “x” igual a 4. Este resultado es la solución de la ecuación.
Una ecuación que aparentemente se observa larga y compleja, se puede resolver de una forma rápida al aplicar la ley de cancelación.
Falta la ley de cancelación para multiplicación y división. ¿Cómo se puede aplicar?
En este caso, para aplicar la ley de cancelación en la multiplicación, se puede eliminar un número o término que esté multiplicando en ambos lados de la igualdad y que se trate del mismo número o término.
Este número o término se debe considerar que sea diferente de cero para poder aplicar la cancelación.
El siguiente ejemplo precisa esta condición.
Se tiene la siguiente igualdad:

“a” por “x” es igual a “b por “x”. El término “x” al multiplicar en ambos lados de la igualdad, se cancela siempre y cuando “x” sea diferente de cero.
El resultado es “a” igual a “b”.
Para aclarar esta situación, se presenta un ejemplo numérico.
En la igualdad, 20 por 7 es igual a 2 por 2 por 5 por 7, en ambos lados está multiplicando el 7 positivo, se aplica la ley y se cancela, el resultado es 20 es igual a 2 por 2 por 5, al realizar las operaciones se obtiene 20 es igual a 20. Se mantiene la igualdad.

En la igualdad 40 por 0 es igual a 2 por 5 por 0, el resultado es cero en ambos lados. Porque 40 por cero es cero, e igual a dos por cinco por cero igual a cero.
Si se aplica la ley de cancelación al número 0, se altera la igualdad porque 40 no es igual a dos por cinco y el resultado es 40 es desigual a 10.
Al no cumplirse la igualdad, es la razón por la cual no es posible eliminar el cero cuando está multiplicando en ambos lados de la igualdad.
Esta consideración sólo es para el cero en el caso de la multiplicación, pero ¿qué ocurre con la división?
En el caso de la división, cuando en una igualdad ambos lados son divididos por la misma cantidad, se puede eliminar de ambos lados.
Se debe cuidar que el divisor afecte a todo el miembro de la igualdad. Se muestra un ejemplo:
“a” entre “x” igual a “b” entre “x”, tiene el mismo divisor, es “x”, que afecta a todo el miembro en ambos lados. Se elimina la “x”.

Para poder eliminar la “x”, debe ser diferente de cero. En caso contrario, genera una indefinición, es decir, el resultado es “a” igual a “b”.
En la ley de cancelación, tanto para la multiplicación como para la división, el número o término por eliminar no debe ser cero.
Observa un ejemplo numérico para la división, s e tienen las siguientes igualdades.
La igualdad 15 más 10 entre 5 es igual a 5^2 entre 5. El resultado en ambos lados es 25.

El 5 como divisor en ambos lados, permite aplicar la ley de cancelación: en el primer miembro quedan 15 + 10 y en el segundo miembro 5 al cuadrado.
Al realizar operaciones 25 es igual a 25. La igualdad se mantiene.
Otro caso es 24 entre 2 es igual a 5 por 4 entre 2 más 2, en ambos lados, el resultado es 12.
La diferencia con la igualdad anterior es que el divisor 2 no afecta a todo el miembro de la igualdad, si se aplica la ley de cancelación para eliminar el divisor 2, el resultado es:
24 es igual a 5 por 4 más 2. Al realizar operaciones, se obtiene 24 es igual a 20 más 2, es decir, 24 es desigual a 22.
En este último ejemplo, no se cumple la ley de cancelación y se altera la igualdad porque el divisor no afecta a todo el lado de la igualdad.
En situaciones algebraicas, es posible aplicar esta ley de cancelación
Realiza el siguiente ejercicio en donde se aplique lo analizado en una ecuación lineal.
Inicia con una ecuación lineal.
5 multiplica a 2x más 3 más 4x, que es igual a 10 x más 39.

Se realiza la multiplicación para eliminar paréntesis, se obtiene 10x más 15 más 4x igual a 10x más 39.
Se aplica la ley de cancelación con 10x en ambos lados de la igualdad, se tiene 15 más 4x es igual a 39.
Se resta 15 en ambos miembros de la igualdad para eliminarlo del primer miembro, se tiene 4x es igual a 39 menos 15.
Por último, se divide entre 4 ambos lados de la igualdad, se elimina el 4 del primer miembro, se obtiene “x” es igual a 24 entre 4, el valor de “x” es igual a 6.
La ley de cancelación se aplica en diversos problemas.
Ahora realiza otro ejercicio:

El perímetro es la suma de todos sus lados y en ambas figuras es el mismo, entonces, se igualan las expresiones.
El perímetro del triángulo es 3 por 3m menos 6, que es igual al perímetro del rectángulo, 2 por 2 m más 4, más 2 por 2 m menos 9.
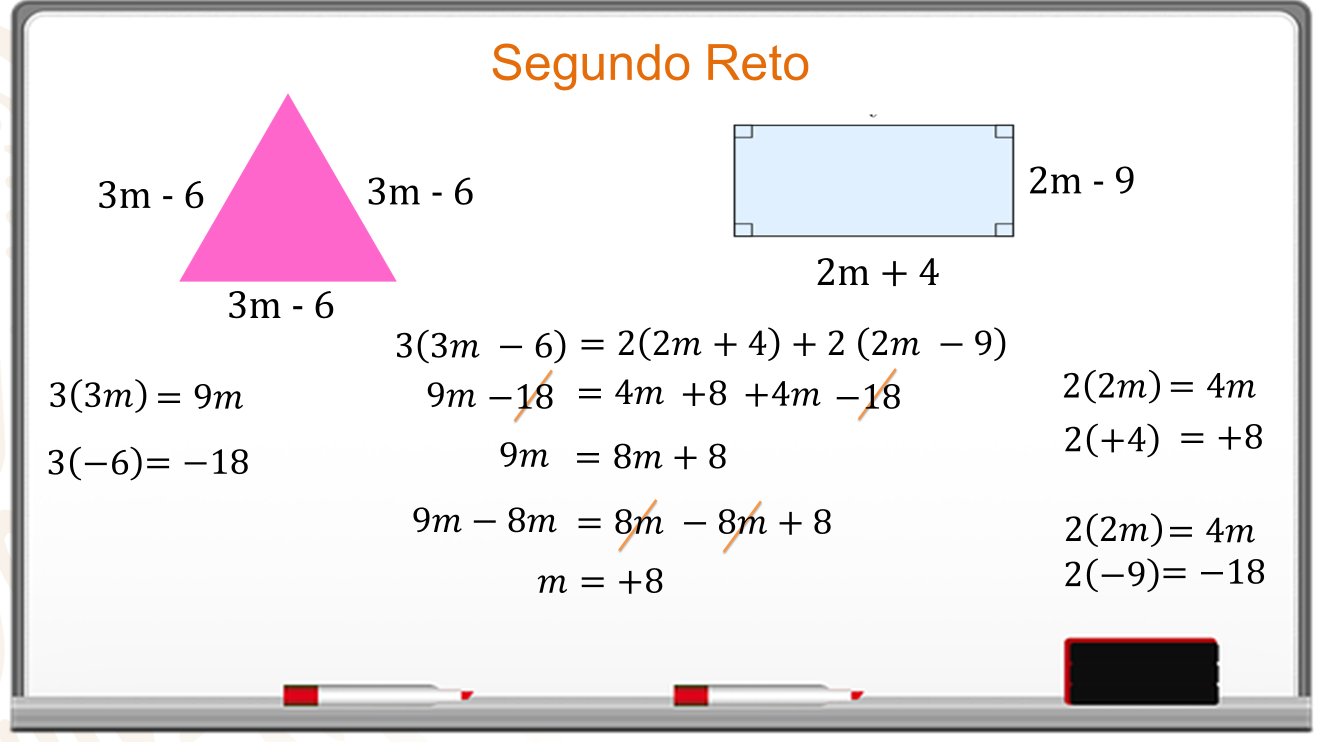
Se realizan los productos y queda:
9 m menos 18 es igual a 4 m más 8, más 4 m menos 18.
Se reducen términos semejantes y se aplica la ley de cancelación para eliminar el 18 de ambos lados, el resultado es: 9 m es igual a 8m más 8.
En ambos lados de la igualdad se resta 8m.
En el primer miembro se reducen los términos semejantes. En el segundo término se cancelan los términos 8 m.
El valor de “m” es 8.
Pero, no se ha resuelto el problema con el cálculo anterior, porque se solicitan las dimensiones de las figuras.
Sólo se sustituye el valor de “m” en las expresiones proporcionadas como medida de los lados de cada figura.
El lado del triángulo es 3 m menos 6, se sustituye el valor de “m”.
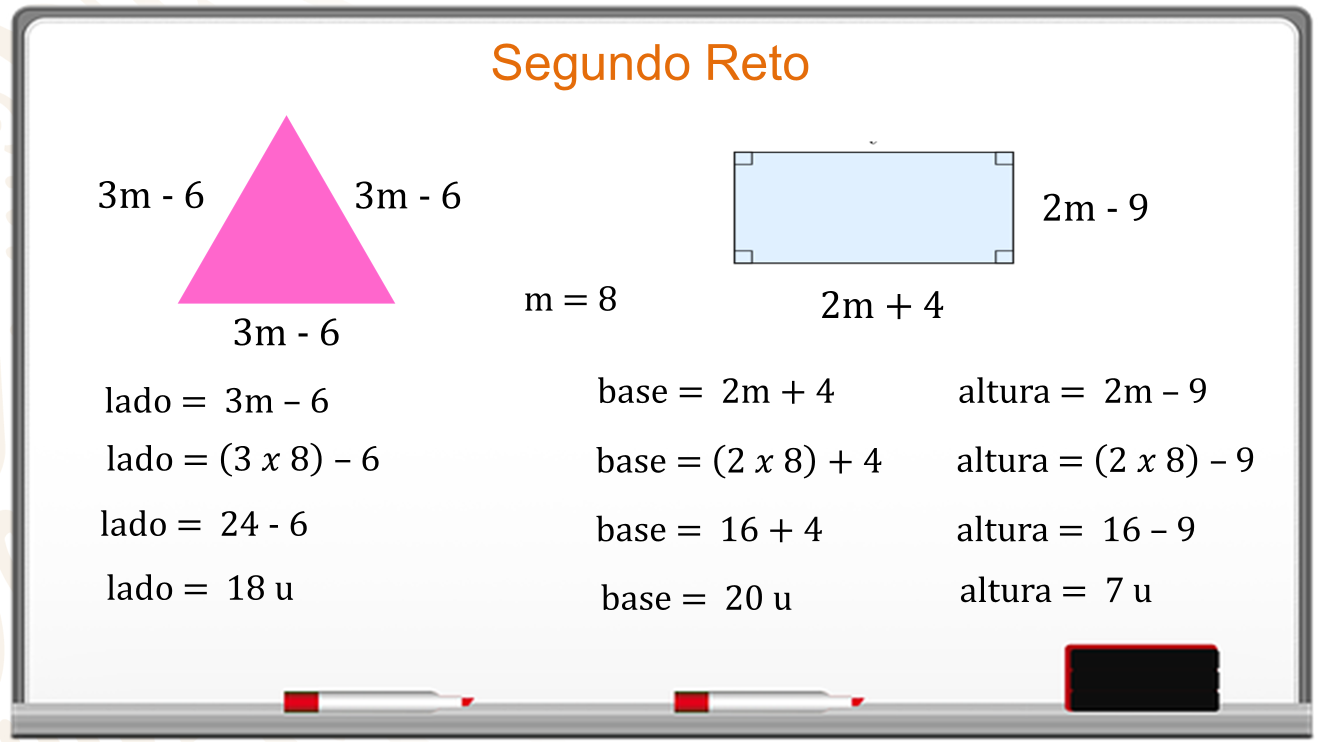
La operación es 3 por 8 menos 6 igual a 24 menos 6 y la medida del lado es de 18 unidades.
El rectángulo tiene como base igual a 2 m más 4, se sustituye el valor es de “m”, es 2 por 8 más 4, igual a 16 más 4. La medida de la base es 20 unidades.
La altura del rectángulo es 2 m menos 9, se sustituye 2 por 8 menos 9, igual a 16 menos 9. La medida de la altura es 7 unidades.
Por último, se comprueba que las dos figuras tienen el mismo perímetro.
Para calcular el perímetro del triángulo se multiplica 3 por la medida del lado que es 18. El perímetro es de 54 unidades.
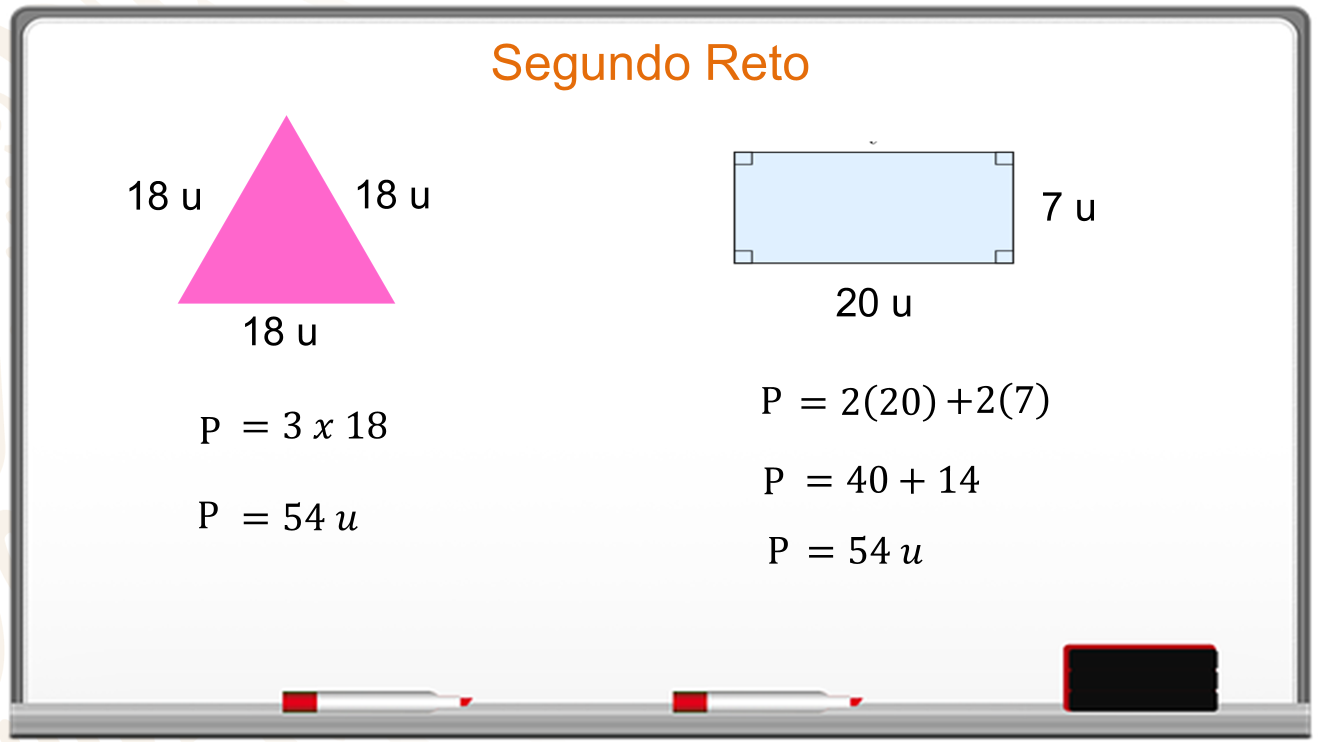
En el caso del rectángulo, su perímetro se obtiene al multiplicar 2 por 20 más 2 por 7. Se hacen las operaciones, 40 más 14 y el perímetro del rectángulo es igual a 54.
Los dos perímetros son iguales.
Las propiedades y leyes facilitan los procedimientos numéricos y algebraicos.
En la ley de cancelación, para todas las operaciones, se deben de considerar dos aspectos:
Para eliminar un número o término, debe de estar en lados contrarios de la igualdad y realizar la misma operación.
Para eliminar un número o término en el mismo lado de la igualdad, la operación del número o término debe de ser inversa para poderla eliminar.
Una reflexión del matemático alemán George Cantor dice: “La esencia de las matemáticas está en su libertad”, en casa, al resolver los problemas y ejercicios aprovecha esa libertad de las matemáticas en tus procedimientos.
El reto de hoy:
Para saber más del tema, busca en tu libro de texto todo lo relacionado y resuelve los ejercicios que ahí se proponen.
Así, podrás enriquecer tu conocimiento y tomar notas en tu cuaderno.
¡Buen trabajo!
Gracias por tu esfuerzo.
Lecturas
https://www.conaliteg.sep.gob.mx/secundaria.html


Login to join the discussion