Las señales de la carretera II
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:46
Aprendizaje esperado: construcción de la fórmula para calcular el área del rombo.
Énfasis: deducir la fórmula para calcular el área del rombo considerando la relación entre sus diagonales y el rectángulo.
¿Qué vamos a aprender?
Aprenderás cómo obtener el área de un rombo.
En esta sesión continuaremos aprendiendo cómo obtener el área de un rombo. Recuerda que en la clase anterior analizamos situaciones que nos pueden ayudar a comprender cómo lograrlo. Vamos a obtener el área del rombo para realizar los señalamientos viales.
¿Qué hacemos?
Recuerda algunas ideas respecto al rombo:
Un rombo se obtiene tomando un triángulo y trazando unas líneas perpendiculares que se cruzan en el centro del rectángulo, luego se unen los extremos de esas líneas y queda un rombo así.

Así es como se traza un rombo, qué es una figura con sus cuatro lados iguales pero que no todos sus ángulos son iguales.
Recuerda que se calcula el área de un rombo utilizando una cuadrícula y contando los cuadritos que están dentro del rombo.
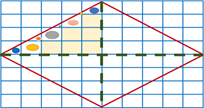
Para calcular el área primero debes contar los cuadritos de uno de los cuatro triángulos que están en cada cuadrante, después multiplicar el número de cuadritos por cuatro, porque el rombo tiene cuatro triángulos iguales y con eso obtienes el área del rombo.
Como recordarás, no es necesario contar cuadrito por cuadrito para obtener el área porque, en cada cuadrante se forma un rectángulo y el triángulo es su mitad, entonces puedes multiplicar la base por la altura de cada rectángulo y dividirlo entre dos.
El triángulo es la mitad del rectángulo de cada cuadrante.

Después de obtener el área de cada triángulo multiplica por cuatro, porque son cuatro cuadrantes, así obtendrás el área del rombo.
Al final sabrás cómo obtener el área de cualquier rombo, como el de los siguientes señalamientos:


Ahora falta calcular el área de los rombos para saber cuánta lámina se debe comprar para elaborarlos, recuerda que en la ferretería la lámina se vende por unidades cuadradas, metros cuadrados, decímetros cuadrados o centímetros cuadrados.
-
¿Tú sabes qué otras cosas se miden con metros cuadrados?
Las losetas para poner el piso en casa y los terrenos también se venden por metros cuadrados.
Recuerda que todas las superficies se miden en unidades de medida cuadradas, metros, decímetros, centímetros.
Los señalamientos no están en una cuadrícula, por lo que debes saber cuántos cuadros tienen.
Tu tarea será descubrir de qué manera puedes obtener el área de los señalamientos o de cualquier otro rombo, aunque no estén en una cuadrícula. ¿Qué podemos hacer?
Recuerdas la sesión anterior donde se veía la cuadrícula y se observa que hay dos triángulos en cada uno de los cuadrantes del rectángulo, entonces quiere decir que de un mismo rectángulo se pueden obtener dos rombos. Para saberlo basta con poner los triángulos sobrantes del rombo.
Observa, para entender mejor.

Observa que si tomas los triángulos color naranja restantes que se formaron al cortar el rombo obtendrás otro rombo así:
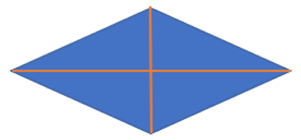
Como puedes ver entonces, un rombo tiene la mitad de área del rectángulo.
Con esto, puedes ver que hay dos rombos con la misma área dentro de un rectángulo, por lo tanto, se podría decir que un rombo tiene la mitad de área de un rectángulo.
Un rombo es la mitad del área de un rectángulo; esto te puede ayudar a calcular el área de un rombo.
Ahora, ve esta imagen para poder descubrir la fórmula para obtener el área de cualquier rombo.
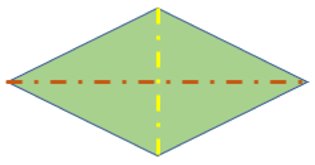
Como puedes ver el rombo tiene dos líneas que lo cruzan, recuerda que esas líneas se llaman diagonales.
Observa que la diagonal naranja es más larga que la amarilla, entonces tiene una diagonal más grande que la otra; llamaré “diagonal mayor” a la naranja, y “diagonal menor” a la amarilla, y como puedes ver en la siguiente figura, la diagonal mayor es la base del rectángulo y la diagonal menor es la altura.
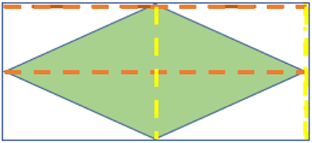
Si las diagonales miden lo mismo que la base y la altura de un rectángulo y todos los rombos tienen la mitad del área de un rectángulo, entonces puedes multiplicar la diagonal mayor por la diagonal menor, lo que te daría el área de un rectángulo, porque sería su base y su altura.
Como el rombo tiene la mitad de área del rectángulo, entonces lo que te resulte de multiplicar las diagonales lo dividirás entre dos y ya tienes el área del rombo.
Así podrás calcular el área de cualquier rombo y para que no se te olvide la podemos escribir como una fórmula. Para hacerlo, primero debes recordar que el rombo no tiene base ni altura, pero tiene “diagonales”, una más grande que la otra, por lo tanto, la fórmula para calcular el área de cualquier rombo será: “Diagonal mayor por diagonal menor entre dos” y la podemos escribir de manera abreviada así:

Lo que significa: “A” es área, la “D” mayúscula es la diagonal mayor, la cruz significa “por” y la “d” minúscula la diagonal menor. La línea debajo de ellos significa “entre”, es decir, dividir entre dos.
Como se ve en la figura la diagonal mayor es la naranja, y la diagonal menor es la amarilla. Puedes ver también que en la formula he marcado con naranja la “D” de diagonal mayor y de amarillo la “d” de diagonal menor.

La fórmula se lee, “El área de un rombo es igual a la diagonal mayor por la diagonal menor entre dos”.
Ya tienes la fórmula, ahora calcula las áreas de los señalamientos y así podrás saber cuánta lámina se debe comprar. Utiliza la fórmula para calcular el área del siguiente señalamiento.
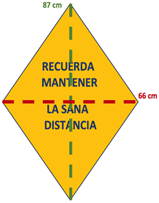
La diagonal mayor, la verde mide 87 centímetros y la diagonal menor, la roja mide 66 centímetros. La fórmula será:
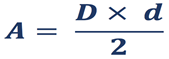
El área es igual a Diagonal mayor por diagonal menor entre dos, entonces sustituye las medidas en la fórmula. Teniendo que diagonal es 87 por diagonal menor que es 66, y ya con números o sea con los valores numéricos del señalamiento, la fórmula queda así:
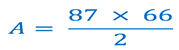
Multiplica 87 por 66, son cinco mil setecientos cuarenta y dos. Ahora te falta dividir 5,742 entre dos.
¿Cuánto te resultó?
R = Dos mil ochocientos setenta y uno.
El área del rombo es de 2,871 centímetros cuadrados. Para que tengas una idea un metro cuadrado tiene diez mil centímetros cuadrados, es decir, diez mil cuadritos de un centímetro.
Ahora calcula el área del siguiente señalamiento.
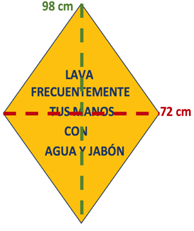
La diagonal mayor mide 98 centímetros y la diagonal menor mide 72 centímetros, sustituye en la fórmula las letras por los valores numéricos del señalamiento.
EL área es igual a diagonal mayor o sea 98 por diagonal menor que es 72, entre dos, ve cómo quedó:

Lo que quiere decir que debes realizar la multiplicación de 98 por 72, son siete mil cincuenta y seis, 7,056.
¿Qué debes hacer ahora?
La fórmula dice diagonal mayor por diagonal menor sobre dos, así que ahora tenemos que dividir 7,056 entre 2, lo que es la mitad, es decir, cuando se divide entre dos resulta la mitad de la cantidad y la mitad de 7,056 es 3,528. Entonces, el área del señalamiento es de 3,528 centímetros cuadrados.
El señalamiento tiene un área de 2,871 centímetros cuadrados y el anterior de 3,520 centímetros cuadrados, de manera que si los sumas en total se necesita comprar 6,391 centímetros cuadrados de lámina.
Ya sabes cómo calcular el área del rombo y porque la fórmula es así. Gracias a los señalamientos ahora sabes que para calcular el área de cualquier rombo se multiplican las diagonales y el producto se divide entre dos y que esa fórmula se escribe así:

Has descubierto cosas sobre el rombo; desde la manera más fácil de dibujarlo, el nombre de las líneas que lo trazan y la fórmula para calcular su área.
El reto de hoy:
Te invito a realizar diferentes rombos con papel y obtener su área.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/



Login to join the discussion