Las funciones

Las funciones

Aprendizaje esperado: consolida contenidos del eje: número, álgebra y variación.

Énfasis: integrar contenidos del tema: funciones.

¿Qué vamos a aprender?

En esta sesión consolidarás algunos conceptos y procedimientos del tema funciones, tales como la variación lineal y la variación proporcional directa e inversa.

¿Qué hacemos?

Una función es una relación entre dos cantidades variables. Existen varios tipos de funciones, pero ahora empezarás por la función lineal, que en este caso está dada por una variación lineal.

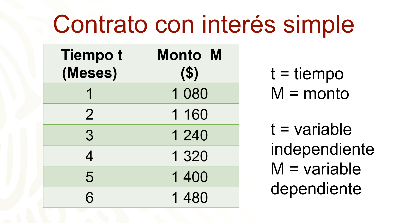
Analizarás una tabla, la cual relaciona dos cantidades variables. Se trata de un contrato mediante interés simple. La primera columna de la tabla exhibe la cantidad referida al tiempo que se invirtió una cantidad de dinero, la segunda es la cantidad llamada monto, que se obtiene por la inversión del dinero.

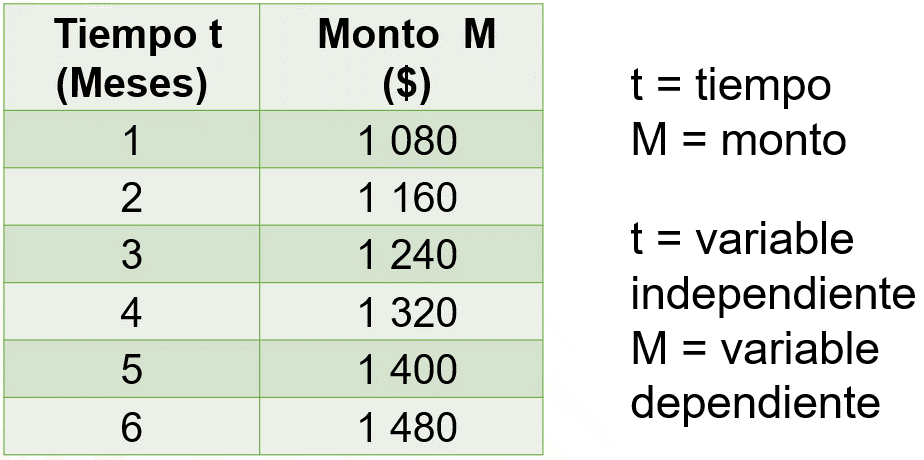
La cantidad “tiempo” es una variable porque cambia de valor, en este caso, entre 1 y 6 meses; la cantidad monto “M” en pesos, también es una variable porque cambia de valor de acuerdo con la variación del tiempo.

A la cantidad “monto” se le conoce como variable dependiente, porque depende del tiempo o los meses que el dinero esté invertido, en cambio a la cantidad “tiempo” se le conoce variable independiente, porque esta no depende del monto.

Se trata de una variación lineal porque su gráfica es un segmento de línea recta. La relación que existe entre estas variables, el tiempo y el monto, se puede expresar mediante una tabla, una gráfica o una expresión algebraica.

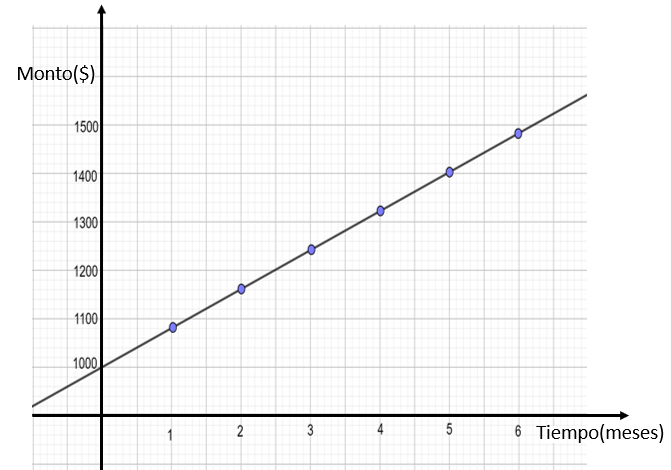
En la gráfica, la variable “tiempo” se encuentra en el eje de las “x” o de las abscisas, mientras que la variable “Monto” se ubica en el eje de las “y” o de las ordenadas. Se han marcado algunos puntos, por ejemplo, la coordenada 5 coma 1 400, indica que, en 5 meses, el dinero invertido se ha convertido en 1 400 pesos.

En un mes la cantidad que se obtiene por la inversión es 1 080 pesos. ¿Qué sucede con esa cantidad cuando el tiempo es cero meses? ¿Cuál es la coordenada del punto por donde la recta cruza al eje “y”?

El tiempo cero meses significa que aún no se ha invertido dinero. En la gráfica, esta situación se representa por la coordenada (0,1000). Observa que la recta cruza por el punto “1000” en el eje “y” y que son 1 000 pesos la cantidad invertida.

La relación entre estas variables también se puede expresar mediante una expresión algebraica. En este caso la expresión es:

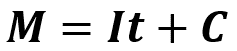
Donde “M” es el monto, “I” es el interés, “t” es el tiempo y “C” es la cantidad invertida. Esta fórmula se utiliza para cualquier cantidad que se quiera invertir.

En cambio, la expresión “M” es igual a 80 “t” más mil, es la fórmula específica para cuando se ha invertido mil pesos, a un interés mensual del 8 por ciento. Esto significa que ganará 80 pesos por cada mes que pase. Por lo tanto, pasados 3 meses se obtienen 1240.

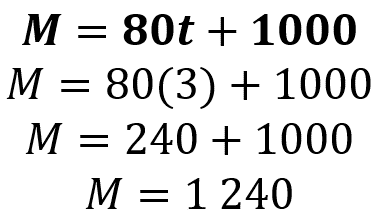
Observa que, si cambiamos las letras de las cantidades variables, y si en lugar de “t” escribimos “x”, y en lugar de “M” escribimos “y”, la expresión algebraica de esta función se reescribe como “y” es igual 80 “x” más 1 000. Pero ¿para qué hacer este cambio?

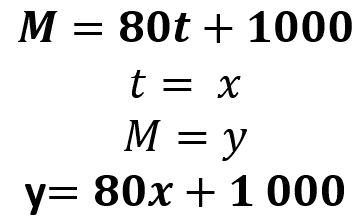
Es importante porque una forma general para una función lineal se puede expresar como:

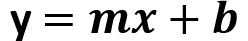
Si comparas está expresión general con la que se refiere a la situación del interés, verás que “x” es el tiempo y “y” es el monto, entonces, ¿cuánto valen los parámetros “m” y “b”?

Observa la siguiente gráfica para estudiar los parámetros “m” y “b” de la forma general. La gráfica representa la relación entre las variables “e” y “p”.

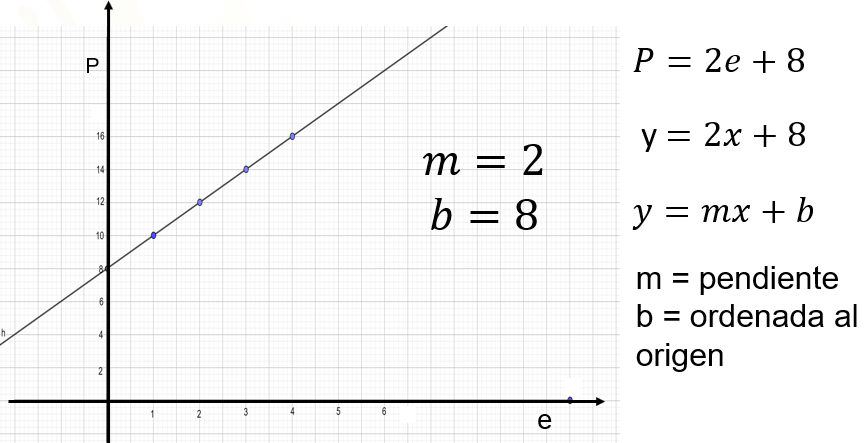
Esta función está dada por la expresión general “p” es igual a 2 “e” más 8. Si cambiamos las variables “p” y “e” por “y” y “x” respectivamente, obtenemos la expresión “y” igual a 2 “x” más 8. Ahora, si la comparas con la forma general “y” igual a “m” “x” más “b”, te podrás percatar que “m” vale 2 y “b” vale 8. El parámetro “b” es 8. ¿Cómo se relaciona esto con la gráfica?

El segmento de recta pasa por el número 8 del eje “y”, entonces el parámetro “b” es igual a 8. A este parámetro se le conoce como ordenada al origen, porque la coordenada de este punto es (0,8), donde la abscisa es 0 y la ordenada es 8. Y el parámetro “m” que en este caso vale 2, ¿cómo se relaciona con la gráfica?

La “m” es la pendiente de la recta, que se relaciona con su grado de inclinación. Una forma de calcular este valor a partir de la gráfica es así: se toman los puntos “L” y “N”. Luego se forma un triángulo rectángulo con líneas punteadas y la gráfica. La idea es obtener el cociente entre las distancias de los lados “N” “O” y “L” “O”.

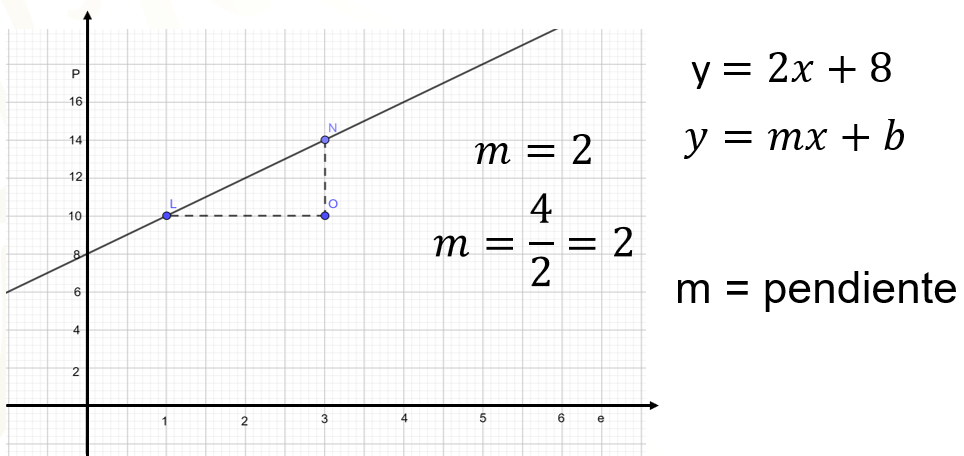
Independientemente de la escala que se use, el segmento “N” “O” mide cuatro unidades, ya que de 10 a 14 hay cuatro unidades, como se ve en el eje “y”; así también se aprecia que el segmento “L” “O” mide 2 unidades ya que de 1 a 3 hay 2 unidades. Ahora, dividiendo la longitud “N” “O” entre “L” “O”, es decir, 4 entre 2, se obtiene 2, que coincide con el valor de la “m”, que es la pendiente de la recta.

La pendiente de una recta es el cociente de la distancia “y” entre la distancia “x” de 2 puntos de una recta. Se le llama también razón de cambio de la función y significa el cambio que hay entre un punto y otro de la recta. Si eliges otros 2 puntos de esta recta y haces lo mismo, te darás cuenta de que la pendiente seguirá siendo 2.

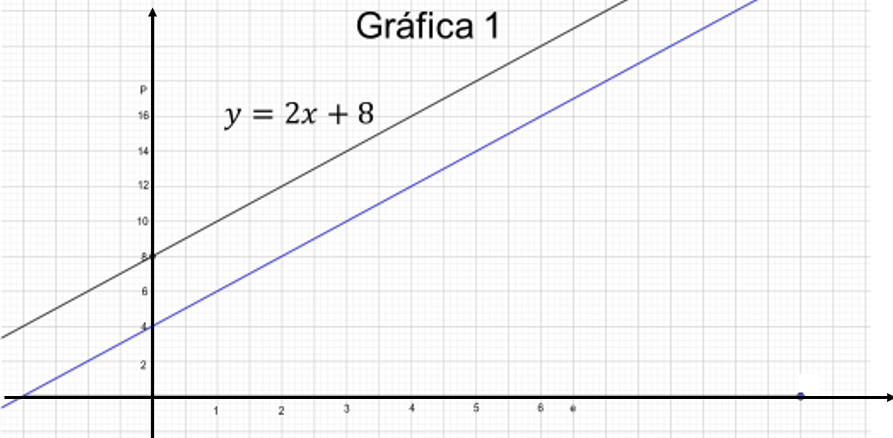
En la gráfica, la recta en color negro representa la función “y” es igual a 2 “x” más 8. ¿Cómo podrías saber cuál es la expresión algebraica que representa la recta azul?

La recta en color azul es paralela a la recta en color negro, por lo tanto, tienen la misma pendiente, o sea “m” debe valer 2. Además, sabemos que en la recta en negro el parámetro “b” es igual a 8 porque cruza al eje “y” en el número 8, por lo tanto, la recta en azul que cruza el eje “y” en el número 4, la letra “b” debe valer 4.

La expresión algebraica de la recta azul es “y” igual a 2 “x” más 4.

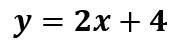
Analiza el siguiente segmento.

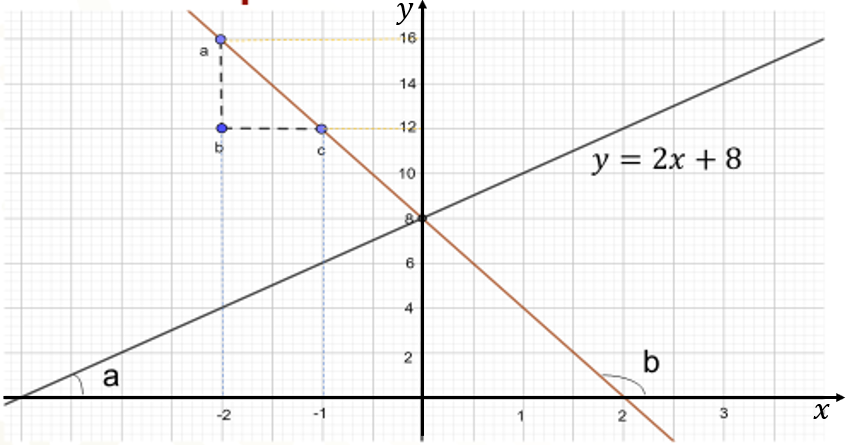
El segmento de recta en color rojo pasa por el mismo punto que el segmento de recta en color negro en el eje “y”, entonces decimos que tiene la misma ordenada al origen, es decir, que la letra “b” vale 8, para ambas funciones. Sin embargo, su pendiente no es igual, porque su inclinación es diferente. Para saber la pendiente, determina el cociente de las medidas de los lados “a” “b” y “b” “c” del triángulo “abc”. La distancia del lado “ab” es 4, como puede verse en el eje “y”, y la del lado “bc” es 1, como puede verse en el eje “x”.

Sin embargo, la pendiente de esta recta no es 4, sino 4 negativo. Al analizar el ángulo “a” que se forma entre la recta en color negro y el eje “x” este es agudo, por ello la recta tiene pendiente positiva. Por el contrario, la recta en color rojo forma el ángulo “b” que es obtuso, y por ello la pendiente es negativa. ¿Cuál es la expresión algebraica de la función que representada por el segmento de recta en color rojo?

La expresión algebraica de la función representada por el segmento de recta roja es:

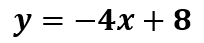
Ahora vas a revisar un tipo de función que además de ser una variación lineal también es una variación proporcional directa entre dos variables.

En el siglo XVII, Robert Hooke promulgó una ley acerca de los resortes; esta ley tiene una explicación más profunda, pero en forma simple, dice que el alargamiento de un resorte se relaciona directamente con la masa que cuelga de él.

En la siguiente tabla se ha denominado con la letra “x” a la masa y con la letra “y” al alargamiento del resorte debido a la masa.

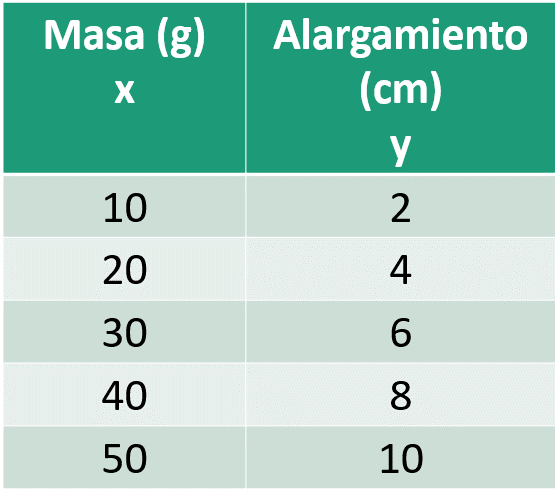
Por ejemplo, para un alargamiento del resorte de 2 centímetros se requiere de una masa de 10 gramos. ¿Es esta una función?

Sí, porque existen dos variables que se relacionan a través de una regla de correspondencia, donde la variable longitud de alargamiento depende de la masa que se requiera para lograr esa longitud. Es, además, una variación lineal porque su gráfica es una línea recta. ¿En que es diferente a la función estudiada antes?

Ambas comparten algunas características. En la presente se puede obtener una constante, representada con “k”. Divide mentalmente las cantidades del alargamiento entre las correspondientes a la masa, tal como 2 entre 10. ¿Cuál es el resultado de las divisiones?

El resultado de todas las divisiones es un quinto, por eso decimos que existe una constante “k” igual a un quinto.

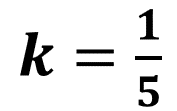
Para obtener la constante se realizó, en general, la división “y”, que representa al alargamiento, entre “x”, que representa a la masa, esto lo podemos expresar como “k” igual a “y” entre “x”.

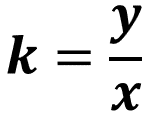
Si despejamos “y” obtenemos la expresión algebraica que designa a la variación proporcional directa, o sea, “y” es igual a “k” “x”.

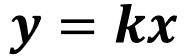
Por otra parte, dado que en esta situación la constante vale un quinto, al sustituirla por la “k” obtenemos “y” es igual a un quinto “x”, expresión que corresponde a la variación proporcional directa de esta situación.

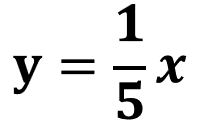
Podemos comparar la expresión algebraica “y” igual a un quinto “x” de la variación proporcional directa con la forma general de una variación lineal. Recuerda que ésta se representa por la expresión “y” es igual a “m” “x” más “b”, entonces, “m” vale un quinto, pero como no está sumada por otro número, entonces “b” es igual a cero.

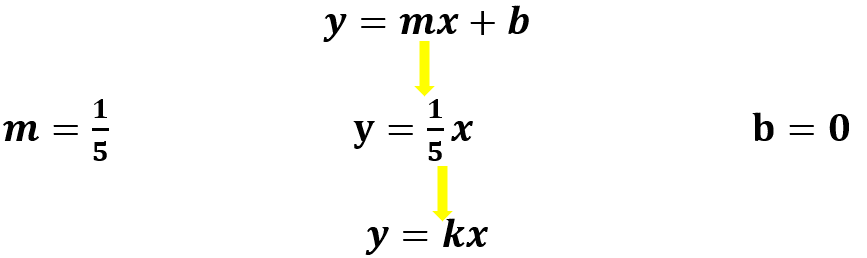
Como la forma general de una variación proporcional directa es “y” es igual a “k” “x”, tanto la pendiente “m” como el valor de la constante “k” coinciden. En el ejemplo de la ley de Hooke, ambas valen un quinto. ¿Podrás prever cómo será la gráfica de esta variación proporcional?

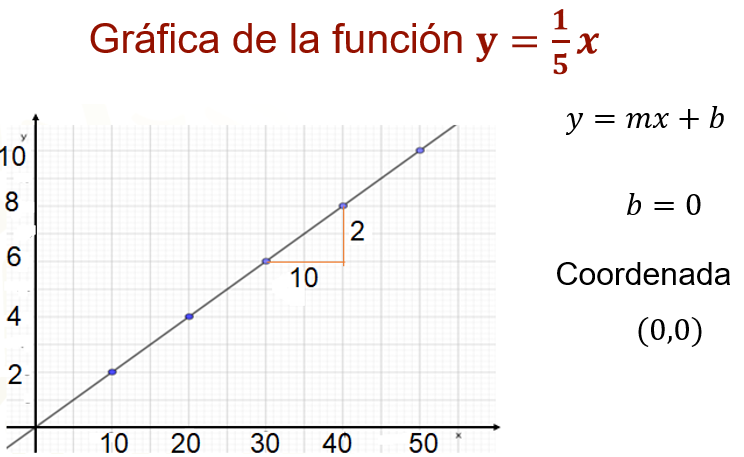
La gráfica de una variación proporcional directa también es una línea recta, sin embargo, observa que esta recta pasa por el origen del plano cartesiano. Comparando la función “y” igual a un quinto “x” con la forma general de la función lineal, se observa que el parámetro “b” es igual a cero, porque, como recordarás, esta letra indica la coordenada del punto en que la recta cruza al eje “y”. Esta coordenada es (0,0). Por lo tanto, la ordenada al origen es cero. Por esto, la recta de una variación proporcional directa pasa por el origen del plano.

Si analizas la pendiente verás que, al hacer la división de la medida de los lados del triángulo rectángulo que se trazó, en rojo, el resultado es un quinto, ya que 2 entre 10 es un quinto. En la variación proporcional directa, la pendiente coincide con la constante, por ello decimos que “m” es igual a “k” igual a un quinto.

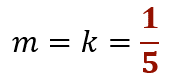
Ahora verás otro tipo de variación entre dos variables, la variación proporcional inversa.

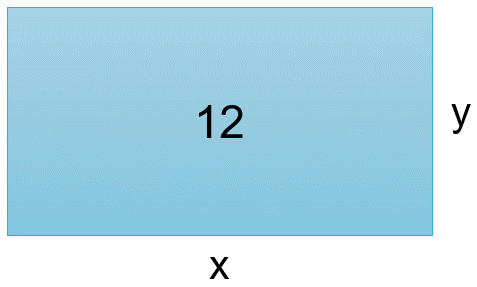
Un rectángulo mide de área 12 unidades cuadradas, y solamente la nombraremos como 12. Llamemos “x” a la base y “y” a la altura de este rectángulo. ¿Cuáles son sus dimensiones? Es decir, ¿cuánto debe medir la base y cuánto la altura para que su área sea de 12?

Tenemos el caso en que la base mide 4 unidades y la altura, 3 unidades, el área del rectángulo se obtiene al multiplicar 4 por 3 que es igual a 12.

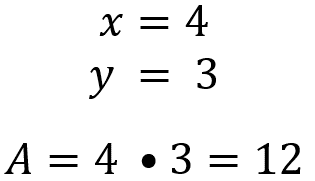
Entonces decimos que las dimensiones del rectángulo son 4 de base y 3 de altura, pero ¿esta es la única solución del problema?, ¿existen otras medidas para la base y la altura que den como resultado el área?

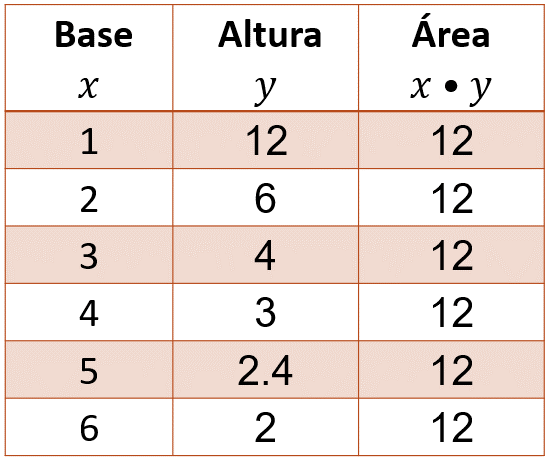
En la tabla se han incluido otras dimensiones que pueden tener la base y la altura del rectángulo todas las cuales dan por resultado un área de 12. Así, si la base mide 2, la altura mide 6, y si la base mide 5, la altura mide 2 punto 4.

Existen otras medidas para la base y la altura, que no se encuentran en la tabla. Podrías preguntarte ¿cuánto debe medir “y” si “x” vale 12? En este caso el valor de “y” es 1.

O también podrías preguntarte ¿cuánto mide “y” si “x” vale 1.5? Se puede buscar un número que multiplicado por 1.5 sea igual a 12, pero esto equivale a realizar la división 12 entre 1.5.

¿Qué otros números podemos asignar a la base?, ¿podemos asignar 1.1, 12.5 o 15? En realidad, es correcto asignar cualquier número real a la base y así calcular la altura para que el área sea 12. Al multiplicar las magnitudes de “x” por las correspondientes de “y” el resultado siempre es 12, por eso se dice que existe la constante 12 y se designa con la letra “k”. En general, en la variación proporcional inversa, para obtener la constante “k” se multiplica “x” por “y”.

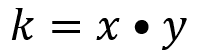
¿Cómo queda la expresión si despejamos “y”?

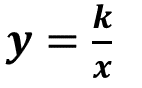
Esta expresión algebraica designa la forma general de una variación proporcional inversa. En el caso del área del rectángulo, sustituimos la “k” por el número 12 obteniendo la expresión:

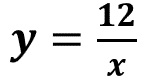
Con esta expresión podemos calcular la altura “y” para cualquier valor de la base “x”.

Observa en la tabla que, mientras los valores de la base aumentan, los de la altura disminuyen. Una característica de la variación proporcional inversa es si los valores de una de las variables crecen, los de la otra, decrecen en la misma proporción.

La siguiente gráfica representa la situación del área del rectángulo, que corresponde a una variación proporcional inversa. En el eje “x” se ubican los valores de la base del rectángulo y en el eje “y”, los de la altura. La gráfica es una curva llamada hipérbola.

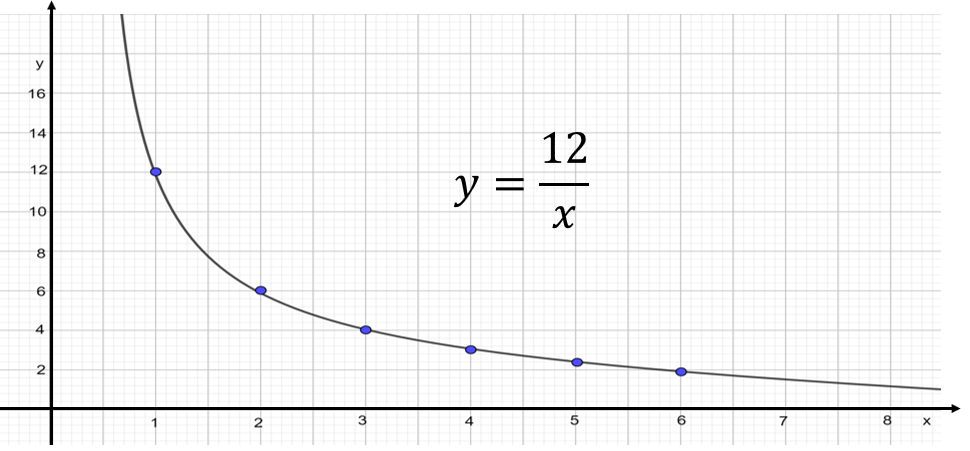
En la hipérbola los puntos en azul corresponden a las dimensiones de la base y la altura que se dieron en la tabla. Sin embargo, es muy importante saber que no sólo estos puntos corresponden a la gráfica, de hecho, ésta se forma por una sucesión de puntos, que corresponden a cualquier número real.

Analiza la hipérbola. ¿La gráfica es creciente o decreciente? Se dice que esta es una gráfica decreciente, porque cuando aumentan los valores en el eje de la “x”, los valores en el eje “y” disminuyen. Por ejemplo, cuando “x” vale 1, el valor de “y” vale 12, en cambio, conforme el valor de “x” va aumentando a 2, 3, 5, etcétera, los valores de “y” van disminuyendo a 6, 4, 2 punto 4, etcétera.

Esta grafica es decreciente, pero existen intervalos en los que la gráfica decrece más rápido que en otros. Por ejemplo, en el intervalo 1 a 3, es decir, en la región de la gráfica que va desde “x” igual a 1 hasta “x” igual a 3, los valores de “y” decrecen muy rápidamente. Para aclararlo compara las unidades en el eje “x” que son sólo 2, de 1 a 3, con las de “y” que son 8, de 12 a 4. En cambio, en el intervalo de 4 a 6, las unidades en el eje “x” son 2, mientras que en el eje “y” es sólo media unidad.

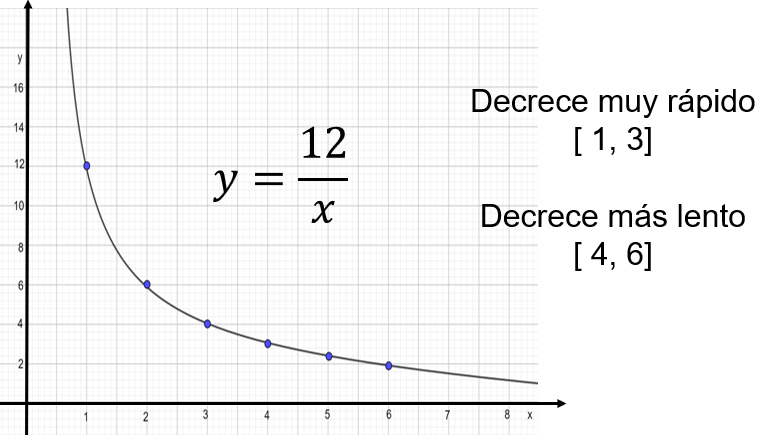
En la gráfica, mientras los valores de la “x” se acercan más a cero, la curva se acerca cada vez más al eje “y”. ¿La variable “x” puede tomar el valor cero?, ¿a qué punto en el eje “y” corresponde este valor? En realidad, esto es imposible, ya que implicaría encontrar un resultado para la división 12 entre cero.

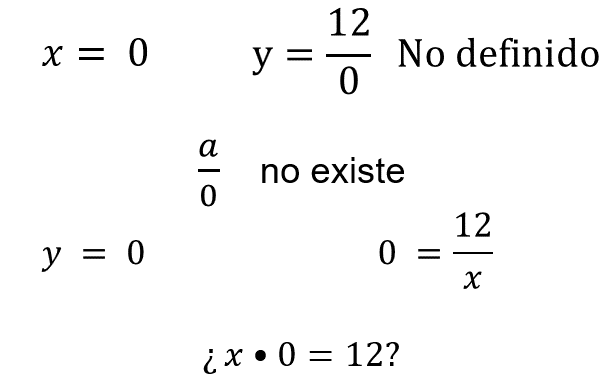
No existe tal valor, porque esa división simplemente no está definida. Es decir, no existe la división entre cero, por ello, lo hemos denotado con la expresión “a” entre cero no existe. Asimismo, “y” no puede tomar el valor de cero, porque esto implica que, al sustituir el valor de “y” en la expresión “y” es igual a 12 entre “x” y despejar “x”, exista un número que, al multiplicarlo por cero de igual a 12.

Entonces, por más que se acerquen los valores de “x” y “y” a cero nunca tomarán este valor, lo que en la gráfica se puede interpretar como el hecho de que la curva se acerca cada vez más a ambos ejes, pero nunca los toca. Por ello, los ejes funcionan como asíntotas de la curva. Las asíntotas son las rectas que cada vez están más cerca de una curva, pero no llegan a tocarla. En el contexto del problema se puede decir que la base del rectángulo no puede ser cero, de lo contrario el rectángulo no existe.

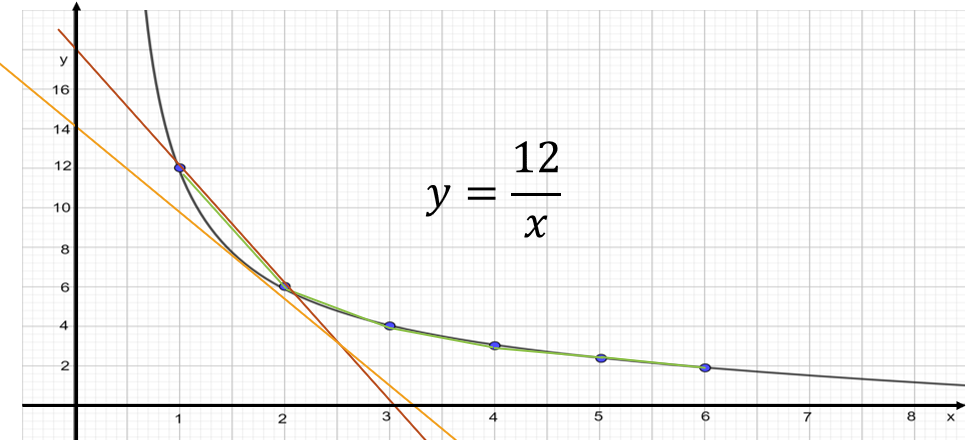
Se comete el error de graficar una curva a través de unir los puntos con segmentos de recta como los que aparecen en color naranja. Esto significaría que la pendiente de la curva es constante, lo cual no es así. Si así fuera, al tomar dos puntos cualesquiera de la curva la pendiente sería la misma, como sucede con las rectas. A simple vista, la pendiente de la recta en azul es diferente a la pendiente de la recta en verde y ambas en el mismo intervalo para valores de “x”.

La pendiente de una curva varía de punto en punto, en cada punto de la curva la pendiente es diferente. Significa que los puntos de los segmentos no son los mismos que los de la curva, por ello, es un error graficar la hipérbola con segmentos de recta. Los extremos de estos segmentos coinciden con los de la curva, pero los demás no, por lo tanto, al sustituir estos en la expresión algebraica no cumplen con la regla de correspondencia.

Para concluir, compara algunos rasgos de dos variaciones trabajadas en esta ocasión.

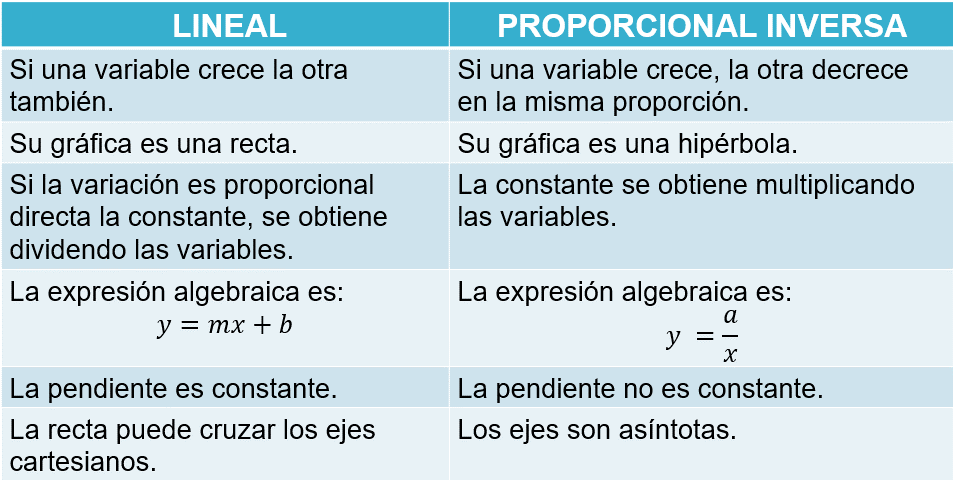
¡Buen trabajo!

Gracias por tu esfuerzo.

* Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html