La subasta de los divisores
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:57Aprendizaje esperado: determina divisores o múltiplos comunes a varios números. Identifica, en casos sencillos, el mínimo común múltiplo y el máximo común divisor.
Énfasis: resuelve problemas que impliquen determinar divisores comunes de dos o tres números.
¿Qué vamos a aprender?
Determinarás divisores o múltiplos comunes a varios números; identificarás, en casos sencillos, el mínimo común múltiplo y el máximo común divisor; y resolverás problemas que impliquen determinar divisores comunes de dos o tres números.
¿Qué hacemos?
Resolverás problemas interesantes a través de divisores comunes de dos o tres números, en la “subasta de divisores”. Pero, ¿Qué es una subasta? ¿En qué consiste?
Una subasta es una forma de vender objetos, ahí las personas deciden cuánto quieren pagar por dicho objeto, hasta que se llega a la cantidad más alta, a partir de la cual ya nadie ofrece más dinero. Para la subasta necesitas recordar lo que trabajaste en el desafío 38. Observa el siguiente video.

-
Video. #AprendeEnCasa III. 6º Primaria. Matemáticas. Una respuesta inesperada 24 de febrero 2021
https://www.youtube.com/watch?v=6mpuuaswjvI
Seguramente recordaste lo que trabajaste en esa sesión, se trató sobre los múltiplos y divisores. Este tema también se abordó en las últimas dos clases. Los divisores son aquellos números que dividen de manera exacta a otro número y su residuo es cero.
Por ejemplo, 3 es divisor de 9
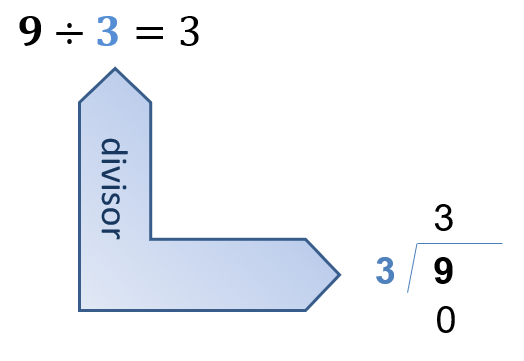
Es cierto, porque 9 entre 3 es igual a 3 y su residuo es cero.
Después del repaso, continúa y juega, ¡La “Subasta de divisores”! Escribe tus propuestas en una hoja o cuaderno. Recuerda, las reglas del juego son las siguientes:

Reglas del juego.
-
Contar con un subastador.
-
Tener el objeto a subastar.
-
Cuando se subasta se indica una cantidad inicial a subastar por el objeto. Sólo podrá ser una cantidad que lo divida exactamente.
-
Jugadores, no pueden hablar hasta el momento en que se abre la subasta y solamente lo harán para dar las cantidades que ofrecen por el objeto de interés.
-
Gana el que ofrezca la máxima cantidad, siempre y cuando no haya un jugador que ofrezca más.
Es un juego fácil, juega ahora. ¡Empieza! Observa la tabla en la cual debes anotar el 60 y 30, los números que se van a subastar.
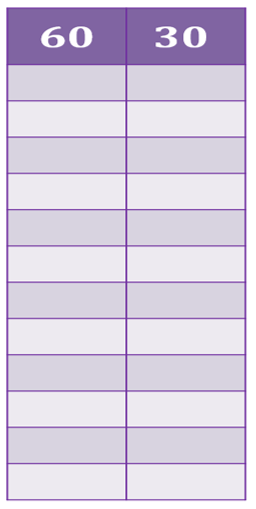
Puedes empezar por el más grande. Registra en la tabla la cantidad que ofrezcas. ¿Cuánto ofreces para comprar el 60? Si es un peso, anota un peso. Si otras personas juegan contigo y ofrecen 5 pesos, registra 5. Tal vez 10, 15, 20, 30 ó hasta 60 que es el máximo pues los divisores no pueden ser mayores que el número que se vende. Anótalos todos.
Vendido el 60 en 60. Han comprado el número 60 ya tienen ese número. Ahora vas a analizar si lo que ofrecieron cumplían con la condición de dividir exactamente al número en subasta.
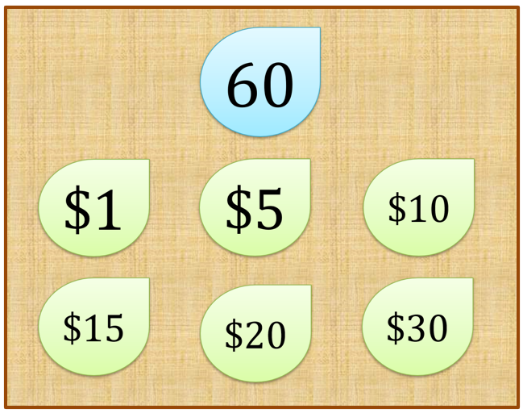
Por el 60 se ofrecieron las siguientes cantidades, 1 peso, 5 pesos, 10 pesos, 15 pesos, 20 pesos, 30 pesos y 60 pesos. ¿Qué relación observas entre las cantidades que se ofrecieron y el 60? Observa detalladamente.
¿Ya encontraste la relación de estos números con el 60? Observa que 30 es mitad de 60 el 15 es la mitad de 30 por lo tanto 15 es la cuarta parte de 60. Bien, pero ¿Cómo puedes comprobarlo? Tal vez puedes utilizar una división.
60 entre 30 es igual a 2 y su residuo es cero
Ahora, 60 entre 15 es igual a 4 y su residuo 0
Como puedes ver el 30 es divisor de 60 ya que lo divide en dos partes iguales y no sobra nada, y si divides 60 entre 2 el cociente es 30 por lo tanto, se comprueba que 2 y 30 son divisores de 60
Entonces debe ocurrir lo mismo con la otra división, cuando 4 divide a 60 el cociente es 15 y tiene como residuo 0. Ahora, si divides 60 entre 15 da 4 y no hay residuo, por lo tanto, 4 y 15 también son divisores de 60
Ya encontraste 4 divisores del número 60, el 2, 4, 15 y 30 ¿Crees que hay más números que son divisores de 60? Observa que el número 60 termina en cero, entonces el número 10 también puede ser su divisor.
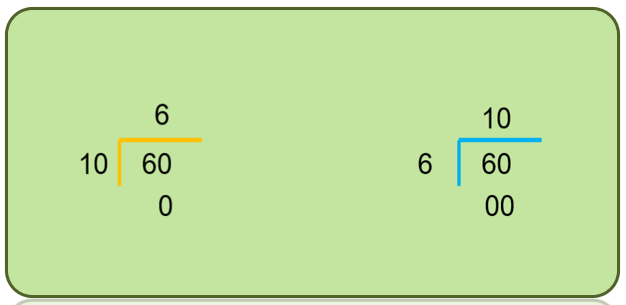
60 entre 10 da 6 y de residuo es 0 y también si divides 60 entre 6 da 10 entonces otros dos divisores son el 6 y el 10. Ahora analiza lo siguiente, la mitad de 10 es 5 ¿5 será divisor de 60?
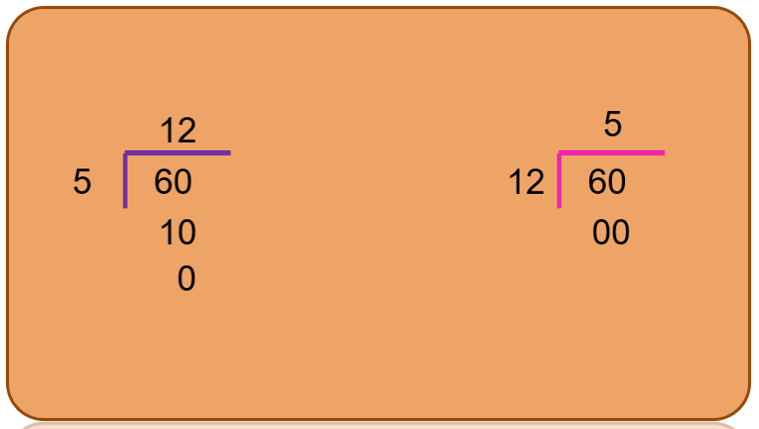
Esto lo puedes corroborar al realizar la siguiente división, 60 entre 5 que da 12 por lo tanto, al dividir 60 entre 12 da 5 y residuo 0
Ahora sólo falta comprobar que 60 y 1 son divisores de 60. Recuerda que todo número dividido entre él mismo da como resultado uno y el residuo es cero, por lo tanto, 60 es divisor de él mismo. También recuerda que cualquier número que se divida entre uno, su resultado es el mismo número y el residuo es cero, entonces también el 1 es divisor de 60
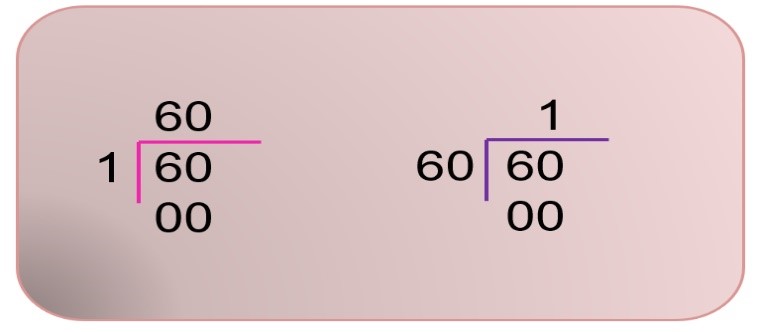
Esto es muy importante, el uno es divisor de todos los números y cualquier número es divisor de él mismo.
Ahora observa al número 30 si lo subastan tal vez lo puedes comprar, porque ya sabes cuáles son todos los divisores de 30

Observa los divisores que están en la tabla. ¿Qué relaciones y características observas entre esos números? Pues que algunos de estos números coinciden en ambas columnas. Obsérvalos.

Todos los divisores de 30 también son divisores del 60 a estos números se les conoce como divisores comunes, porque son divisores de dos o más números, y su residuo siempre es 0
El 1, 2, 3, 5, 6, 10,15 y 30 son divisores comunes de 30 y de 60
También el 60 y el 30 son múltiplos comunes de 1, 2, 3, 5, 6, 10, 15 y 30
¿Qué te parece? Estas relaciones que siempre se encuentran entre los números son interesantes.
Ahora es momentro de pasar al libro de texto, desafío 74 página 137
https://libros.conaliteg.gob.mx/P6DMA.htm?#page/137

La consigna del problema 2, con sus dos incisos, dice lo siguiente:
Problema 2. En la ferretería tienen dos tambos de 200 litros de capacidad. Uno contiene 150 litros de alcohol y los otros 180 litros de aguarrás. Se decidió mandar hacer varios garrafones del mismo tamaño y capacidad para envasar tanto el alcohol como el aguarrás sin que sobre nada de líquido en los tambos.
Inciso a) ¿Es posible que la capacidad de los garrafones sea de entre 10 y 20 litros? ¿Por qué?
Inciso b) Escriban tres capacidades diferentes que pueden tener los garrafones.
Es importante recuperar la información del problema. Tienes 2 tambos de 200 litros de capacidad. Uno tiene 150 litros de alcohol y el otro tiene 180 litros de aguarrás. El Aguarrás es un líquido incoloro que se utiliza como diluyente de pinturas o barnices, es semejante al thinner.
Ahora que ya tienes claridad de los conceptos de los productos que se van a manejar, recuerda que se requieren garrafones del mismo tamaño y capacidad para envasar los líquidos, debes estar atento o atenta, pues no debe sobrar nada.
Analiza la información: Hay dos tambos con 150 litros y 180 litros, respectivamente, que tienes que dividir en garrafones del mismo tamaño, entonces, piensa en buscar un número que divida exactamente al 150 y al 180

Recuerda que estás buscando la capacidad del garrafón que sirva para repartir ambos líquidos.
Nota que el 150 y el 180 terminan en 0 así que significa que las dos cantidades se puede dividir entre 10 por lo tanto, una conclusión es que se pueden utilizar garrafones de 10 litros para envasar ambos líquidos y no sobra nada.
¿Cuántos garrafones necesitarías para cada uno de los líquidos? Para el alcohol, 15 garrafones y, para el aguarrás, 18 ahora comprueba las respuestas. Si tienes 150 litros de alcohol y lo repartes en garrafas de 10 litros, entonces llenarás 15 garrafones porque al dividir 150 entre 10 el cociente es 15
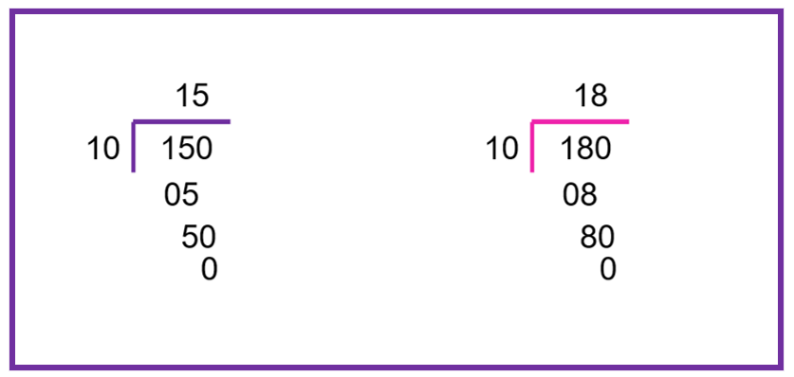
Tienes 180 litros de aguarrás y lo distribuyes en 18 garrafones de 10 litros cada uno, porque 180 entre 10 da como cociente 18
Con esto, sabes que sí puedes utilizar un garrafón de 10 litros para repartir ambos líquidos, pero ¿Has pensado si un garrafón de 20 litros te serviría, así se ocuparían menos garrafones? Bien, pues ve si un garrafón de 20 litros te sirve. Realiza las divisiones.
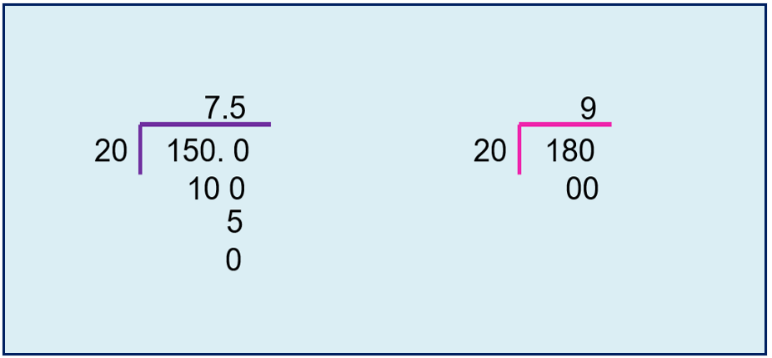
Al hacer las divisiones resulta que no sirve un garrafón de 20 litros. Lo puedes comprobar haciendo las divisiones correspondientes: 150 entre 20 es igual a 7.5 esto significa que necesitas 7 garrafones y la mitad de otro y con eso ya no se cumplen las condiciones del problema, aunque 180 entre 20 es igual que 9 en este caso sí da exacto el número de 9 garrafones, definitivamente, un garrafón de 20 litros no es conveniente, ya que no sirve para envasar ambos líquidos y que no sobre nada.
Con esto, tienes claro que un garrafón de 10 litros te sirve para repartir ambos líquidos y sobra nada, pero busca otras opciones de garrafones, piensa en un garrafón más, que sirva para envasar los dos líquidos.
Necesitas encontrar otro número que divida exactamente al 150 y al 180 y ya comprobaste que 20 no es opción aunque sea el doble de 10 ¿Tal vez lo puedes intentar con 5 que es la mitad de 10?
¿Cómo puedes comprobar si te sirve el 5? Pues haciendo otra división de cada cantidad entre 5. 150 entre 5 es igual a 30 entonces serían aquí 30 garrafones; mientras que 180 entre 5 es igual a 36, 36 garrafones, entonces sí resultó.
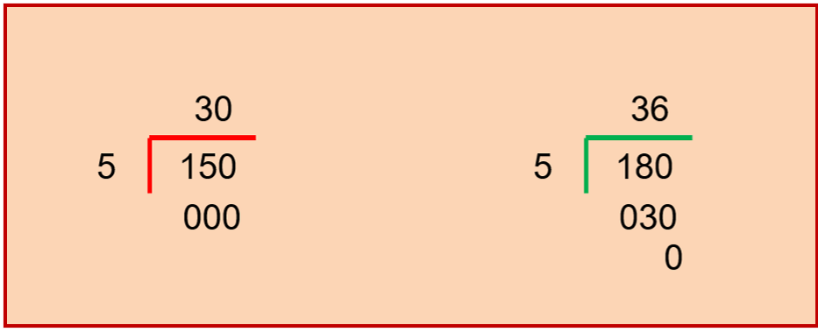
Has encontrado que un garrafón de 5 litros es también una opción para envasar los líquidos sin que sobre nada.
Observa que en el libro dice que llegó un tambo de 105 litros de cloro. ¿Viste que presentación de garrafón te puede servir? Si la capacidad de un garrafón de 5 litros te sirve para repartir los dos primeros líquidos y 105 se divide exactamente entre cinco y no sobra nada, así es pues 105 se puede dividir exactamente entre 5 entonces 105 entre 5 es igual a 21
Entonces para repartir el cloro, necesitas 21 garrafones de 5 litros y nada sobra.
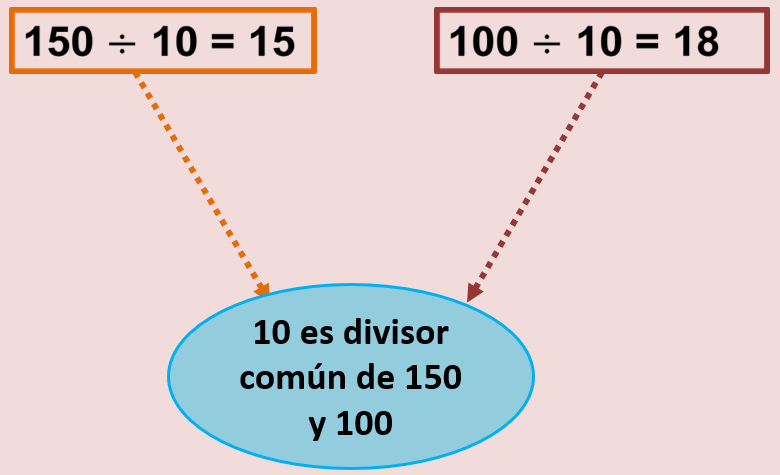
En la primera parte del problema encontraste que un número que divide exactamente a 150 y a 180 es el 10, a este número lo llamamos divisor común.
Después encontraste que el 5 también es un divisor común de 150, 180 además también de 105 porque al dividir cada cantidad entre 5 da en el cociente un número exacto y en el residuo es cero.
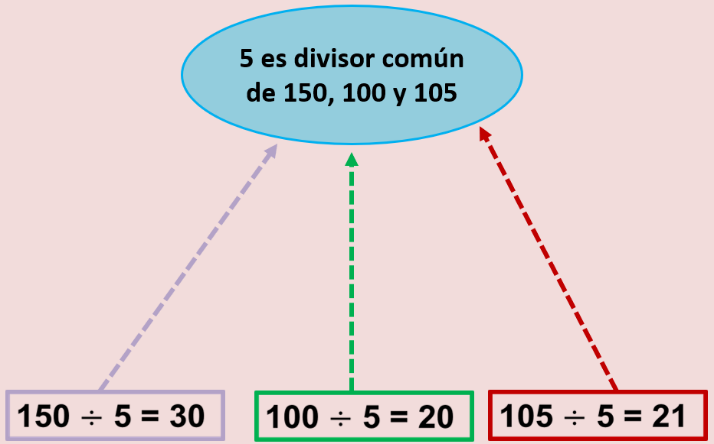
Pensar en los divisores te permite resolver diversos problemas.
Pues aquí tuviste la oportunidad de ver un poco más sobre divisores. Con esta información puedes analizar las situaciones que se te presenten, quizá alguna se resuelva o pueda resolverse con divisores comunes.
El reto de hoy:
Presenta a alguno de tus familiares cercanos alguno de los problemas que hayas resuelto y que haya llamado más tu atención, explícale como lo resolviste y por qué, con seguridad le será muy interesante.
Si te es posible, consulta otros libros o materiales para saber más sobre el tema.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas

https://libros.conaliteg.gob.mx/20/P6DMA.htm











Login to join the discussion