La multiplicación y su relación con la suma iterada
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:06
La multiplicación y su relación con la suma iterada
Aprendizaje esperado: resuelve problemas de multiplicación y división con números enteros, fracciones y decimales positivos y negativos.
Énfasis: justificar la regla de los signos de la multiplicación de números enteros con base en la suma iterada.
¿Qué vamos a aprender?
Profundizarás en las reglas para resolver problemas de multiplicación y división con números enteros y aprenderás a plantear problemas matemáticos. Además, resolverás problemas tanto con números enteros, como con fracciones y números decimales positivos y negativos.
En esta sesión reflexionarás sobre cómo la suma repetida de un mismo sumando, positivo o negativo, se representa también como una multiplicación de números positivos o negativos.
¿Qué hacemos?
Vas a empezar con una lectura de un extracto del libro “A jugar con las matemáticas”, de Lawrence.
¿Cuántos dedos hay?
“… no todo el mundo ha empleado el mismo sistema para contar. Aunque la mayor parte de las civilizaciones que saben hacerlo han tenido como base el diez, hay muchos ejemplos de sociedades que han utilizado bases distintas. Algunas de ellas pueden parecernos sorprendentes. La forma de utilizar nuestro número nos parece tan natural que nos resulta difícil creer que no se haya extendido por el mundo entero. Sin embargo, el sistema decimal es sólo una de las infinitas formas que podíamos haber elegido para sistematizar los números. Si tuviéramos ocho dedos en lugar de diez, por poner un ejemplo, utilizaríamos un sistema de base ocho y nos sentiríamos tan felices como siempre, aunque no podríamos tocar tan bien el piano.
Esto no es una situación hipotética. Aparte del sistema decimal, el sistema numérico más utilizado es el vigesimal o de base veinte. Tanto los mayas como los esquimales tomaron como base el veinte, posiblemente porque contaban utilizando los dedos de las manos y de los pies.”
En la lectura anterior se mencionan algunos ejemplos de cómo en el pasado los seres humanos implementaron procedimientos para resolver problemas de conteo y dieron solución a esta situación haciendo uso de las herramientas disponibles en su contexto.
¿Imaginas cómo en la antigüedad resolvieron el reto de representar el cero? o, ¿cómo se representaban las pérdidas o ganancias?
A continuación, analizarás algunas situaciones de la vida diaria que implican operar matemáticamente con números positivos y negativos.
Empieza por revisar: qué son los números positivos y negativos.

Observa el siguiente ejemplo:
Juan les ganó a sus amigos $15.00 jugando a las canicas.
¿Cómo se representa la cantidad que ganó Juan de manera matemática?
Como Juan obtuvo una ganancia, la cantidad se representa con un número positivo: “quince positivo” y se escribe así: +15 o 15
Ahora, observa el siguiente ejemplo respecto a un caso con números negativos:
Eduardo le debe $20.00 al señor de la tienda.
¿Cómo se puede representar la situación financiera de Eduardo de manera matemática?
Como Eduardo adquirió una deuda, se considera con un número negativo: “veinte negativo” y se escribe así: –20
Después de haber analizado estas situaciones que se pueden representar con números positivos y negativos, reflexiona respecto a lo que se conoce como: suma iterada. Para ello, analiza la siguiente situación.
Retoma el ejemplo anterior de Juan. Ahora, imagina que Juan ganó $15.00 en cada uno de seis juegos consecutivos.
¿Cómo representarías esta situación?
¿Cómo puedes saber cuánto dinero ganó Juan?
Antes de resolver el problema, recuerda que el nombre correcto de la operación matemática que permite agrupar cantidades es “adición” y al resultado se llama “suma”.
Ya que conoces los términos, analiza la situación de Juan:
Si se realiza la adición del número 15, seis veces repetidas.
¿Cuál será el resultado de la suma?
El resultado de la operación es 90, y la operación que representa la situación es:
15 + 15 + 15 + 15 + 15 + 15 = 90
Es decir, al ganar Juan seis veces de manera consecutiva, en total ganó $90.00.
Ahora, analiza cómo la operación matemática de adición que acabas de realizar también puede ser representada de otra manera. Cuando en una adición el mismo número se repite varías veces, esta operación se puede representar y resolver por medio de una multiplicación.
Retoma la suma anterior:
15 + 15 + 15 + 15 + 15 + 15 =
El sumando que se repite en la operación es: 15
Y aparece, 6 veces.
Lo anterior lo puedes representar con una multiplicación de la siguiente manera:
6 veces 15 es igual a:
(6)(15) = 90
Esto representa lo mismo que 6x15
En algunas circunstancias es más apropiado el uso de un par de paréntesis para indicar los factores en una multiplicación, en lugar de utilizar el signo “por”.
Analiza una nueva situación:
Imagina que ahora Juan, en lugar de ganar, pierde $5.00 en cada uno de cuatro juegos consecutivos.
¿Cuánto dinero pierde en total?
¿Con qué operación de adición se puede representar la situación?
¿Qué tipo de números serían los sumandos?
Esta situación implica que los sumandos sean un mismo número negativo, porque se está hablando de una pérdida o deuda.
(–5) + (–5) + (–5) + (–5) = –20
Cuatro veces, cinco negativo
El número que se repite como sumando es: -5
Y este sumando se repite 4 veces.
Lo anterior se puede representar con una multiplicación de la siguiente manera:
4 veces –5 es igual a:
(4) (–5) = –20 que representa lo mismo que 4 x (–5)
El resultado de los ejemplos de adición que acabas de realizar se llama: suma iterada.
La suma iterada es el resultado de la adición de un mismo número o sumando varias veces y se puede representar como una multiplicación.
La multiplicación que representa una suma iterada se forma de la siguiente manera:
- El primer factor corresponde al número de veces que aparece el sumando.
- El segundo factor corresponde al número o sumando que se repite.
Entonces se puede decir que, una multiplicación de números enteros se expresa de distintas maneras.
- Con el símbolo de multiplicación:
4 x (-3) - Sólo con paréntesis:
(4) (-3)
A continuación, realiza la siguiente actividad.
Actividad 1.
Observa los ejemplos de la siguiente tabla, completa el ejercicio de la última fila (donde el resultado es -20) y responde las preguntas.
| Expresión verbal | Adición y suma | Multiplicación y producto |
| Cuatro veces -7 | (-7)+(-7)+(-7)+(-7) = -28 | (4)(-7) = -28 |
| Tres veces -9 | (-9)+(-9)+(-9) = -27 | (3)(-9) = -27 |
| Seis veces -6 | (-6)+(-6)+(-6)+(-6)+(-6)+(-6) = -36 | (6)(-6) = -36 |
| = -20 |
¿Cuál es la multiplicación y producto de -20?
¿Cuál es su adición y suma?
¿Cuál es su expresión verbal?
Ahora, analizarás una situación más.
Esto le pasó a Valeria:

Valeria relaciona la suma iterada con una situación que está en el contexto de dinero: recibir $50 pesos cada domingo durante un mes.
La suma iterada también se puede representar en una recta numérica, que es una herramienta gráfica que permite ubicar números en puntos específicos.
En la recta numérica los números positivos se encuentran a la derecha del cero, y los números negativos están a la izquierda del cero.
Observa los números negativos en el caso del tío de Valeria, se usará una recta numérica.
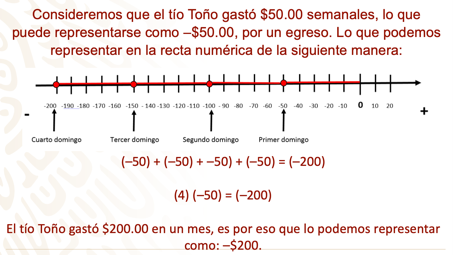
Ahora, analiza la siguiente situación que implica la suma iterada y su representación también como multiplicación.

Producto de dos factores.
Si el primer factor es un número positivo y el segundo factor también es positivo, el producto es un número positivo:
positivo por positivo es igual a positivo
(+) (+) = (+)
Si el primer factor es un número positivo y segundo factor uno negativo, el producto es un número negativo:
positivo por negativo es igual a negativo
(+) (–) = (–)
Observa los siguientes ejemplos sobre el producto de dos factores:
| Tabla del 5 | Tabla del 4 |
| 5 x 2 = 10 | 4 x 2 = 8 |
| 5 x 1 = 5 | 4 x 1 = 4 |
| 5 x 0 = 0 | 4 x 0 = 0 |
| 5 x (-1) = -5 | 4 x (-1) = -4 |
| 5 x (-2) = -10 | 4 x (-2) = -8 |
En esta sesión aprendiste la suma iterada, que te permitió determinar que la adición de un mismo número repetidas veces, puede representarse como una multiplicación.
También reflexionaste sobre la representación de los números positivos y negativos. Así como el producto de dos factores.
El reto de hoy:
Reto 1.
Responde las siguientes preguntas:
¿Cuál es el producto de multiplicar (5) × (–5)?
¿Qué sucede con el signo del producto al multiplicar el primer factor con signo positivo por otro con signo negativo?
¿Cuál es el producto de multiplicar (-3) (20)?
Reto 2.
Piensa en una situación de tu vida cotidiana en la que hayas podido ejemplificar la suma iterada. Escríbelo en tu cuaderno y comparte tus descubrimientos.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/





Login to join the discussion