La fórmula del volumen
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 17:05Aprendizaje esperado: c alcula el volumen de prismas y cilindros.
Énfasis: g eneralizar la fórmula para calcular el volumen de prismas y cilindros.
¿Qué vamos a aprender?
Comprenderás la necesidad de emplear una fórmula general para calcular el volumen de prismas rectos cuya base sea un polígono regular, y para el cilindro. Para ello, realizarás actividades donde observes los cuerpos geométricos, los explores y los compares, con la finalidad de proponer diferentes maneras para calcular su volumen.
En esta sesión, analizarás casos específicos para llegar a la generalización sobre el volumen de los cuerpos geométricos. De esta manera, podrás aplicar las fórmulas a una gran diversidad de problemas.
¿Qué hacemos?
Reflexiona en las siguientes preguntas, mismas que puedes registrar en tu cuaderno e ir respondiendo a lo largo de la sesión.
- ¿Qué se necesita conocer para calcular el volumen de un cuerpo geométrico?
- ¿Cuál es la fórmula para calcular el volumen de un prisma recto y de un cilindro recto?
- Si se conoce el volumen de un prisma y la medida de su altura, ¿qué procedimiento se puede realizar para calcular el área de la base?
Para responder a cada una de las preguntas, realiza el siguiente ejercicio:
Volúmenes de prismas rectos
La imagen que se muestra a continuación representa un prisma recto.
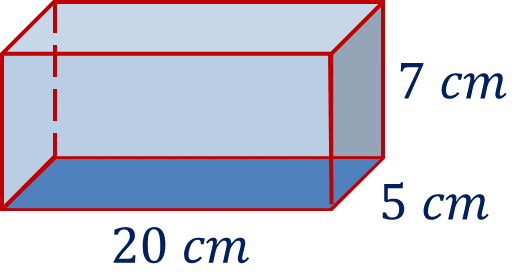
Responde las siguientes preguntas:
- ¿Qué forma tiene la base? El prisma tiene la base de forma rectangular.
- ¿Qué forma tienen las caras laterales del prisma? Las caras laterales del prisma tienen forma rectangular.
- ¿Qué datos se necesitan para calcular su volumen? El ancho y el largo de la base, y la altura del prisma.
- ¿Cuál es la fórmula para calcular el volumen del prisma rectangular?
Volumen es igual al producto del área de la base por la altura del prisma.
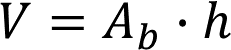
- ¿Cuál es el volumen del prisma?
Para responder, empieza calculando el área de la base rectangular cuya fórmula es base por altura o largo por ancho. Tienes de base un rectángulo cuyas medidas son 20 cm de largo por 5 cm de ancho, sustituye estos valores en la fórmula quedando de la siguiente forma:
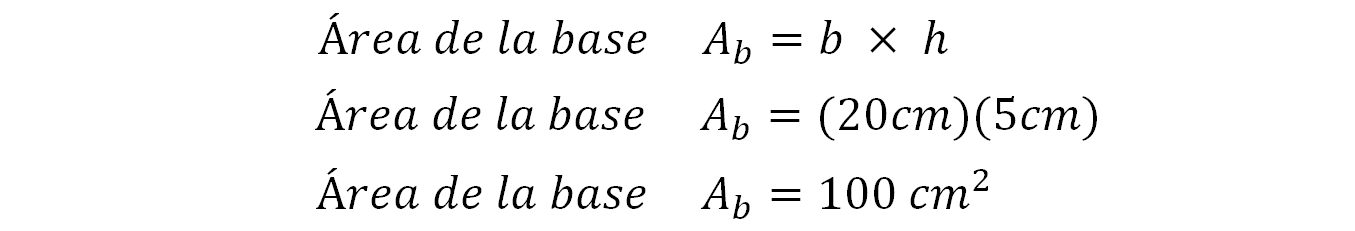
Por lo tanto, obtienes 100 centímetros cuadrados.
Ahora sustituye el área de la base obtenida en la fórmula de volumen. El volumen es igual al área de la base por la altura del prisma.
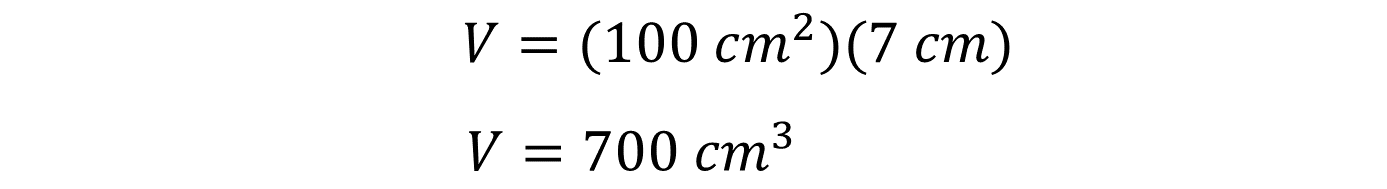
Llevando a cabo el producto, obtienes que el volumen del prisma recto rectangular es igual a 700 cm cúbicos.
Al hacer este ejercicio, se pudo demostrar y aplicar la fórmula para calcular el volumen del prisma rectangular.
Analiza otro cuerpo geométrico:
Observa la imagen de una caja de regalo y su representación como cuerpo geométrico.
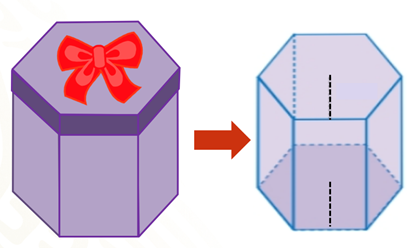
Responde las siguientes preguntas:
- ¿Qué forma tiene la base de la caja? Es una caja que tiene una base con forma de hexágono regular.
- ¿Qué forma tienen las caras laterales de la caja? Las caras laterales tienen forma rectangular.
- Observa detenidamente el prisma de base rectangular y la caja de regalo, ¿en qué son diferentes? Compáralos.

La primera diferencia entre el prisma rectangular y la caja es la forma de sus bases: la caja tiene una base hexagonal, y el prisma tiene base rectangular.
La segunda diferencia es que las caras laterales de la caja son iguales, y las caras laterales del prisma son diferentes.
Ahora, reflexiona:
¿Se utilizan diferentes fórmulas para calcular el volumen de la caja hexagonal y del prisma rectangular?
La fórmula es la misma: área de la base por altura, pero en el caso de la caja, para calcular el área de la base, se usa la fórmula para calcular el área de un polígono regular, es decir, perímetro por apotema dividido entre dos. En cambio, en el prisma rectangular se utiliza la fórmula para calcular el área de un rectángulo: base por altura o largo por ancho. Observa:
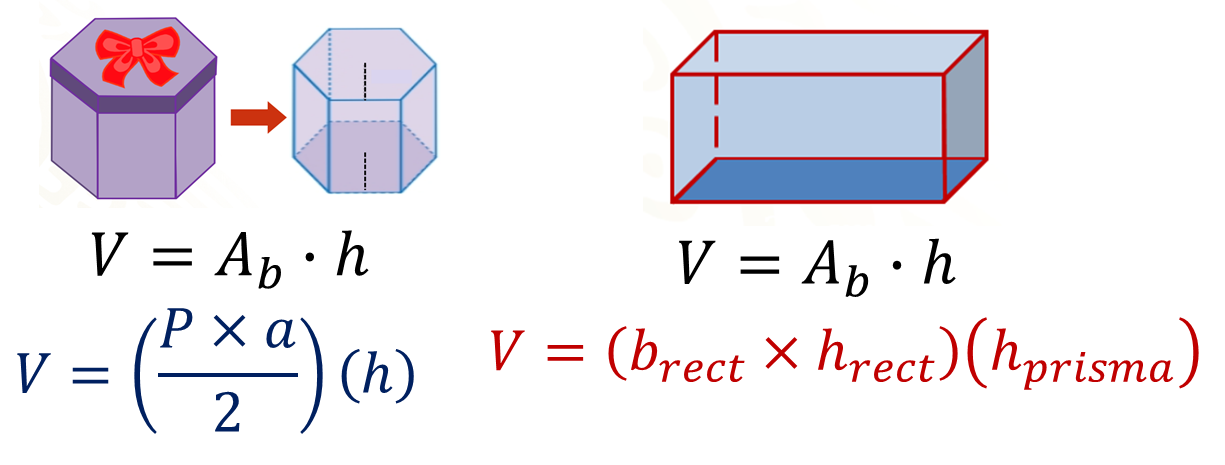
La fórmula para calcular el volumen de cualquier prisma recto es la misma:
V = área de la base por altura.
Lo que cambia es la manera de calcular el área de la base, pero no la fórmula del volumen.
Después de haber profundizado en la fórmula de prismas rectos, calcula el volumen de algunos cuerpos geométricos. Empieza con un prisma de base hexagonal.
Prisma de base hexagonal
La medida de sus lados es igual a 6 metros, su apotema mide 5.2 metros y la altura del prisma es igual a 10 metros.
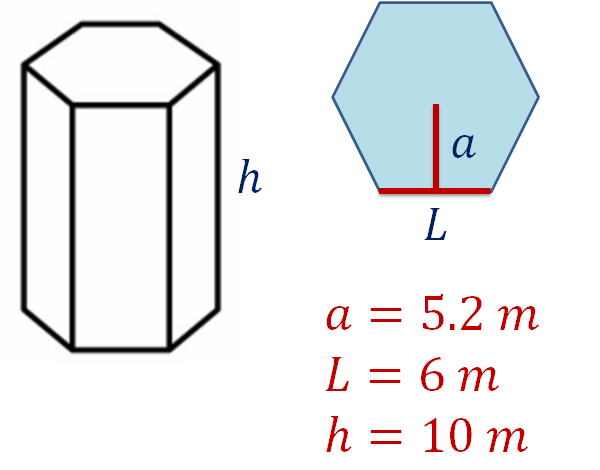
Lo primero que harás, es calcular el perímetro del hexágono regular de la base. Para ello, usa la fórmula:
Perímetro es igual al producto de la medida de los lados por el número de lados
Sustituye los valores en la fórmula:
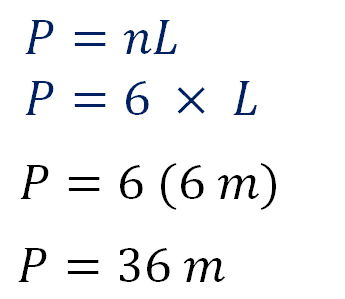
Conoces la medida de la apotema, que es igual a 5.2 metros, y el perímetro es igual a 36 metros, por lo que puedes calcular el área del hexágono:
Área de la base es igual a perímetro por apotema dividido entre dos
Sustituye los valores:
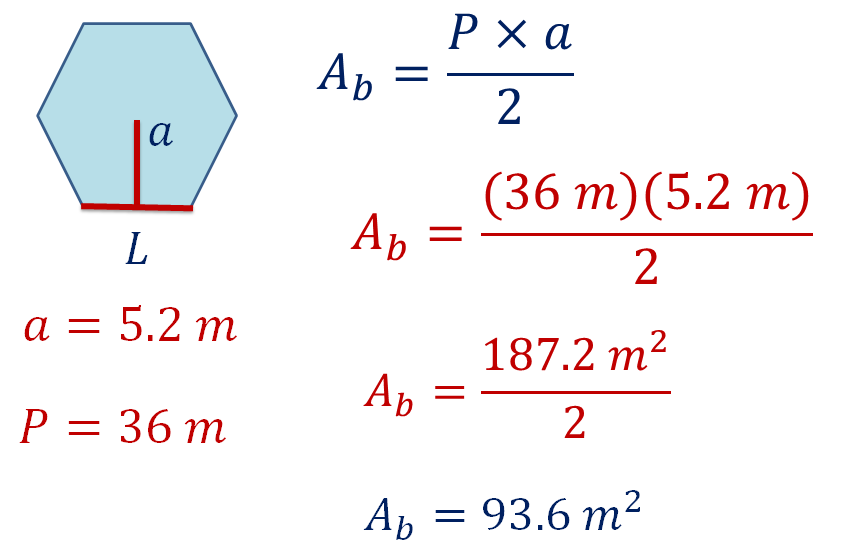
Realizando la operación obtienes: área es igual a 93.6 metros cuadrados.
Para terminar, calcula el volumen del cuerpo geométrico tomando en cuenta la fórmula:
Volumen es igual al área de la base por la altura del cuerpo geométrico
Lleva a cabo la sustitución:
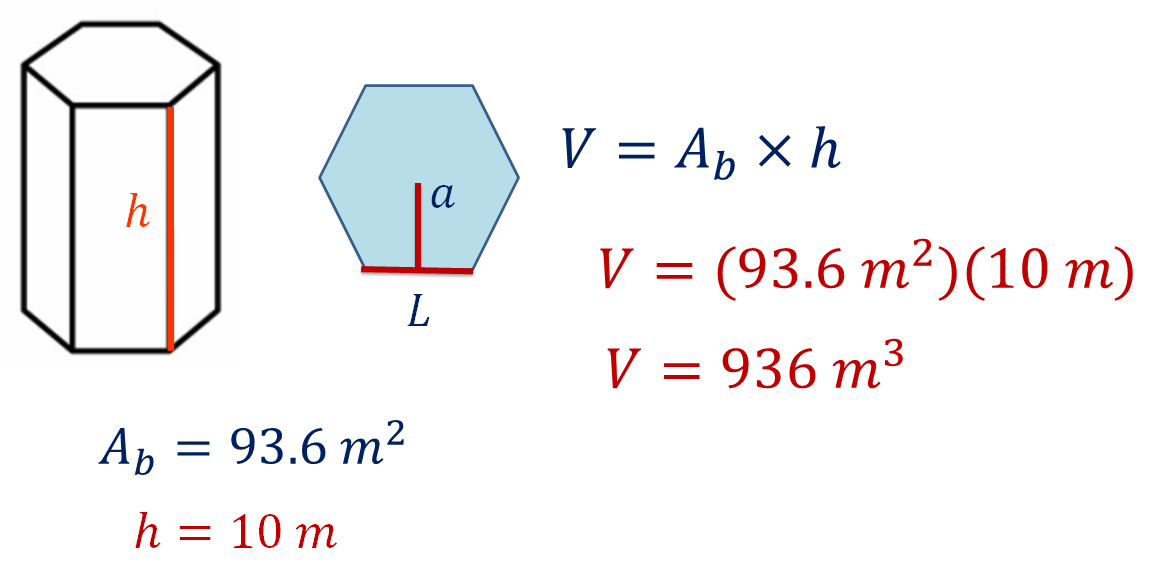
Por lo tanto, obtienes como resultado 936 metros cúbicos.
Entonces:
¿Qué pasos se siguieron para calcular el volumen del prisma hexagonal?
Primero se determinó el tipo de polígono que tiene la base del prisma; en este caso, su base es un hexágono regular, por lo que se trata de un prisma hexagonal. Luego se calculó la medida del área de la base del prisma para, finalmente, calcular el volumen del cuerpo mediante la fórmula: volumen es igual al área de la base por la altura.
Es importante determinar los datos que necesitas para realizar los procedimientos adecuados.
Sigue con otra figura.
Prisma pentagonal
Calcula el volumen del siguiente prisma pentagonal. Los datos que se tienen son: la medida de la apotema de la base pentagonal es igual a 2.06 metros, la medida de cada lado es igual a 3 metros y la altura del cuerpo geométrico es igual a 8 metros.
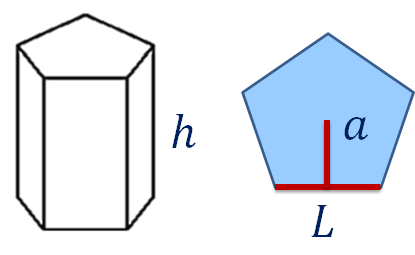
Lo primero que harás, es calcular el área de la base; para ello, calcula el perímetro del pentágono regular con la siguiente fórmula: perímetro es igual a cinco por la medida del lado.
Sustituye el valor del lado en la fórmula:
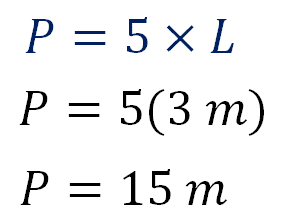
El perímetro del pentágono es de 15 metros.
Como la medida del perímetro es igual a 15 m y la apotema es 2.06 metros, ya puedes calcular el área del pentágono.
Área de la base es igual a perímetro por apotema dividido entre dos. Sustituyendo valores:
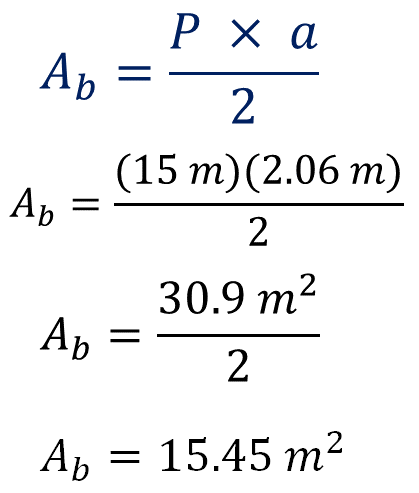
El área es igual a 15.45 metros cuadrados.
Ahora calcula el volumen del cuerpo geométrico tomando en cuenta la fórmula: volumen es igual al área de la base por la altura del cuerpo geométrico.
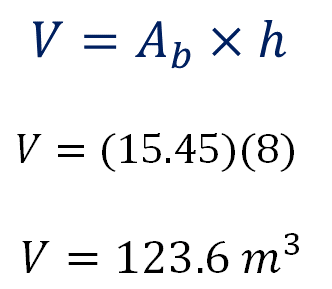
Obtienes como resultado 123.6 metros cúbicos.
A lo largo de la sesión, has ido respondiendo a las preguntas que se plantearon inicialmente. Ya sabes qué fórmula usar para calcular el volumen de prismas rectos y qué elementos necesitas conocer para calcularlo. Sin embargo, ¿qué pasa si se conoce el volumen y la altura de un prisma, pero se desconoce el área de la base? ¿Con qué procedimiento se podría calcular?
Para responder estas preguntas, resuelve el siguiente ejercicio.
Prisma triangular
Tienes un prisma triangular del que conoces su volumen, que es igual a 400 centímetros cúbicos, y su altura, que mide 16 cm, pero desconoces el área de la base.
Calcula el área de la base del prisma triangular:
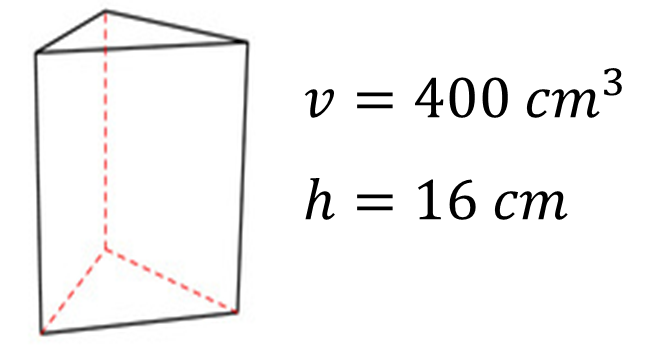
En este caso, en la fórmula del volumen despeja el área de la base, que es lo que necesitas conocer.
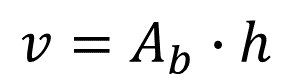
Al despejar el área de la base, como la altura está multiplicando, pasa del otro lado de la igualdad dividiendo, por lo que queda la siguiente expresión:
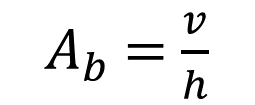
Sustituye los valores del volumen y de la altura, y lleva a cabo la división:
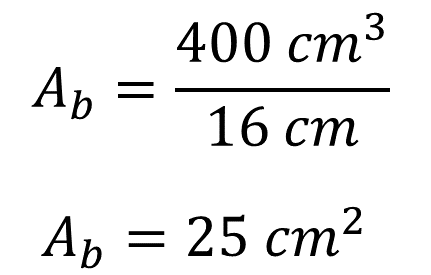
Obtienes 25 centímetros cuadrados, que corresponden al área de la base del prisma triangular.
Ya has realizado diferentes ejercicios, ahora recapitula todo lo que has aprendido hasta el momento.
Un prisma es un cuerpo geométrico que está limitado por dos polígonos paralelos e iguales, que se llaman bases, y por tantas caras laterales con forma de paralelogramo como lados tengan las bases. Según la forma de sus bases, los prismas pueden ser triangulares, rectangulares, poligonales, entre otros.
Un prisma recto es aquel cuyas caras laterales son rectangulares.
Después de profundizar en los prismas rectos, continua con los cilindros. Para ello calcula el volumen de los siguientes cilindros rectos.
Cilindro recto
Calcula el volumen del siguiente cilindro recto:
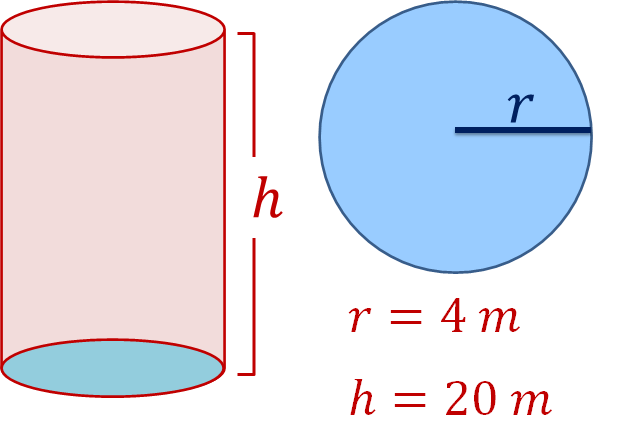
Para calcular el volumen de un cilindro, primero establecerás la fórmula para calcular el volumen. En este caso, se usa la misma que se utilizó con los prismas, es decir, volumen es igual al área de la base por la altura.
Ahora, calcula el área de la base. Tienes como dato: radio igual a 4 m, y como la fórmula para calcular el área del círculo es:
Área de la base es igual a “pi” por el radio elevado al cuadrado, sustituye los datos en la fórmula, el valor de “pi” lo tomarás como 3.14.
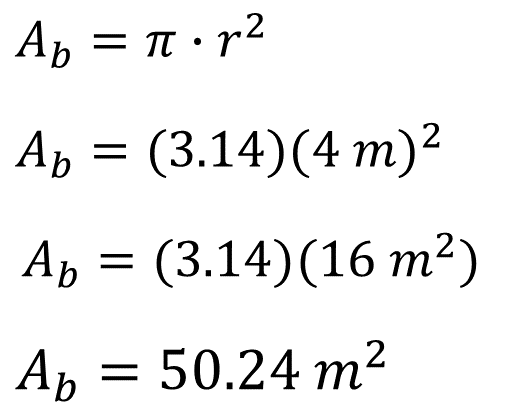
El resultado del área de la base es igual a 50.24 metros cuadrados.
Para terminar, calcula el volumen del cilindro recto multiplicando el área de la base por la altura del cilindro, que en este caso es de 20 metros.
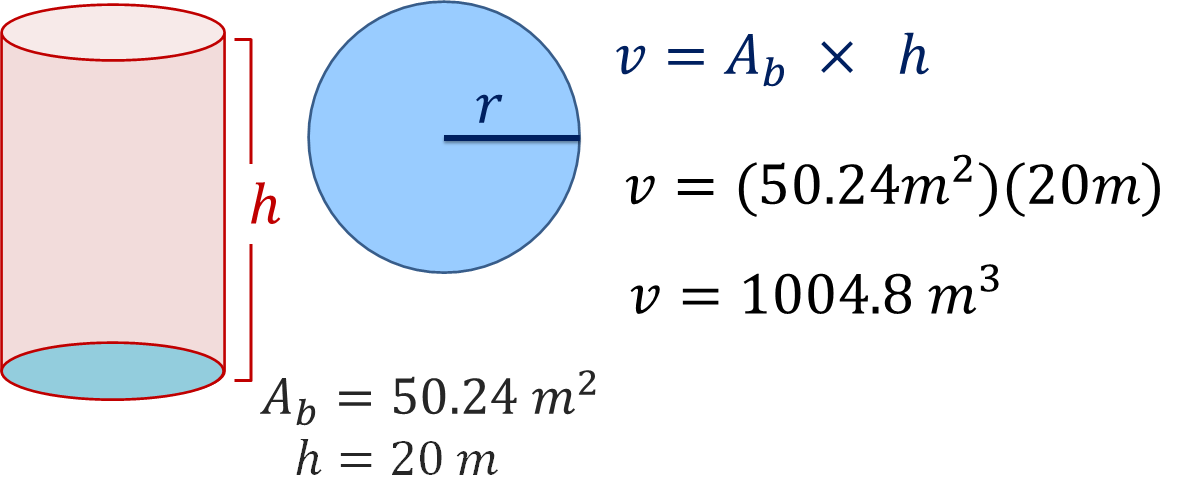
Obtienes como resultado 1004.8 metros cúbicos.
Es importante entender el procedimiento para poder asimilarlo y usarlo en la resolución de otras situaciones.
Ahora, vas a calcular el volumen del siguiente cilindro.
Cilindro recto 2
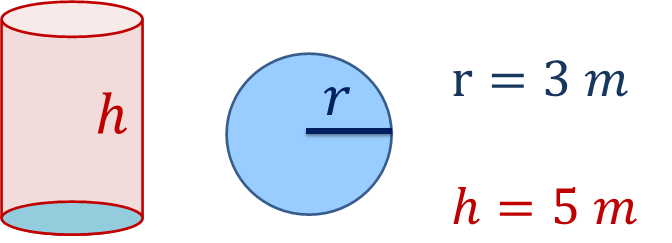
Empieza por calcular el área de la base. Tienes como dato: radio igual a 3 m. Sustituye los datos en la fórmula, el valor de “pi” lo tomarás como 3.14.
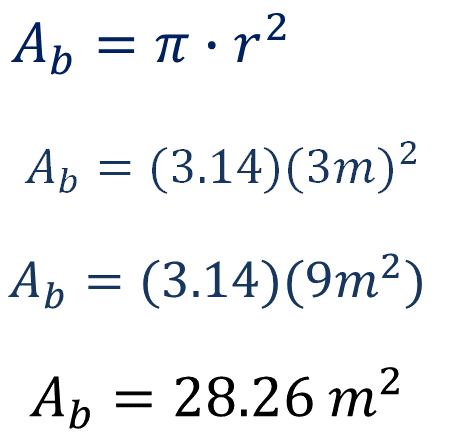
Obtienes como resultado, área de la base es igual a 28.26 metros cuadrados.
Para terminar, calcula el volumen del cilindro. Lleva a cabo la sustitución:
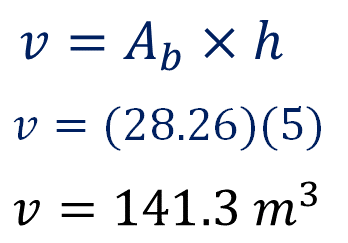
Obtienes como resultado 141.3 metros cúbicos.
Para calcular el volumen de un prisma o de un cilindro, se sigue el mismo procedimiento según los datos con los que se cuenta.
Finalmente, reflexiona en la siguiente pregunta:
¿Es lo mismo volumen que capacidad?
La diferencia está en que todos los objetos de nuestro mundo tienen volumen, mientras que los objetos susceptibles de ser medidos respecto a la capacidad son sólo los recipientes, ya que pueden contener algo.
Hay objetos, como cubos, que tienen un volumen, pero no están huecos, por lo que no tienen capacidad. Y otros, como un envase cilíndrico que puede contener agua, esos sí tienen volumen y capacidad.
Con lo aprendido en esta sesión, ya puedes calcular el volumen de un prisma recto de base poligonal y de cilindros rectos y puedes identificar cómo despejar los elementos de la fórmula para calcular valores faltantes, por ejemplo, la altura o el área de la base.
Recuerden que este es un material de apoyo. Consulta tu libro de texto de Matemáticas de segundo grado. Seguramente encontrarás más actividades que te ayudarán a profundizar en este tema.
El Reto de Hoy:
Resuelve el siguiente problema.
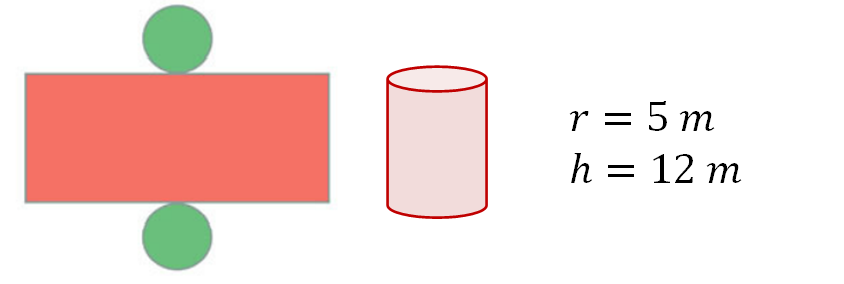
¿Cuál es el volumen del cilindro que resulta al armarse el siguiente desarrollo plano?
Los datos con los que cuentas son los siguientes: radio igual a 5 metros y tiene una altura de 12 metros.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/


Login to join the discussion