La fábrica de tapetes. Las fracciones de la unidad
Valoración de la comunidad:
Última Actualización:
6 de Febrero de 2025 a las 15:36Aprendizaje esperado: Resolución de problemas que impliquen particiones en tercios, quintos y sextos. Análisis de escrituras aditivas equivalentes y de fracciones mayores o menores que la unidad.
Énfasis: Comparar fracciones que se representan gráficamente, al dividir una unidad con ciertas condiciones.
¿Qué vamos a aprender?
Seguirás aprendiendo a comparar fracciones representadas gráficamente, al dividir una unidad o entero.
En la sesión anterior empezaste a estudiar el tema de la comparación de fracciones. Dividiste una unidad (un cuadrado) en medios, cuartos y octavos, y también una unidad (círculo) en tercios, sextos y novenos. Aprendiste a encontrar algunas fracciones equivalentes a través de su representación gráfica.
En esta sesión seguirás estudiando este tema.
Para empezar, realiza la siguiente actividad:
En tu cuaderno traza un cuadro que mida 6 cm por cada lado, (o bien, que tenga 12 cuadritos por lado). Una vez elaborado lleva a cabo lo siguiente:
A 1/2 del cuadro coloréalo de amarillo.

A 1/4 de la superficie coloréalo de rojo. Recuerda que 1/2 = 2/4

Por último, a 1/8 del cuadro ilumínalo de color verde. Recuerda que 1/4 = 2/8

Ahora analiza y responde los siguientes cuestionamientos. Trata se contestar cada pregunta y después confirma tú repuesta con la explicación que se da a continuación.
¿Es verdad que la superficie que falta de color corresponde a 4/16? Explica, ¿Por qué?
La superficie que no tiene color no corresponde a 4/16 ya que la fracción equivalente de 1/8 es igual a 2/16. Si se utilizan cuadros unidad como los de la clase anterior, se puede ver con más claridad:
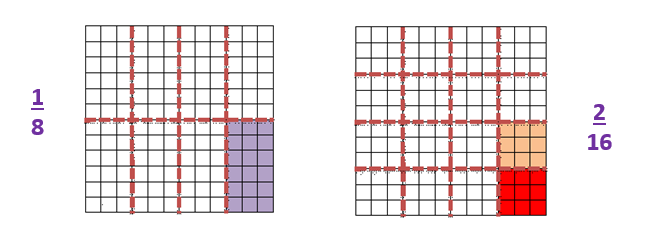
En las siguientes imágenes se observa, con la parte de color rojo, que 4/16 es equivalente a 2/8 y a 1/4

En el siguiente cuadro unidad colorea de anaranjado 1/3 de su superficie sin cubrir los otros colores, ¿Se podría cumplir esta instrucción?

La respuesta es no ya que 1/3 es mayor que 1/8 que es la parte que falta de colorear.
Esto se puede comprobar identificando en un cuadrado igual, las fracciones de 1/3 y 1/8
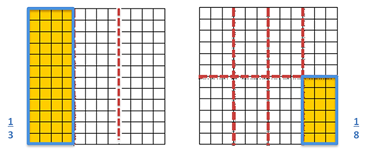
Esta actividad que acabas de realizar te permitirá continuar con el trabajo de la sesión de hoy.
Si tienes libros en casa o cuentas con Internet, explóralos para saber más.
¿Qué hacemos?
Realiza las siguientes actividades.
Traza varios cuadros de 10 por 10 cm o cuadritos.

Divide un cuadro en 5 partes iguales. Para hacerlo, puedes contar los cuadritos que abarca la superficie del cuadrado y corroborar que son 100 cuadraditos, porque cada lado tiene 10 cuadraditos y 10 × 10=100 cuadraditos de área.
Posteriormente divides los 100 cuadraditos entre 5 que son las partes a obtener, y nos da como resultado 20 cuadritos.

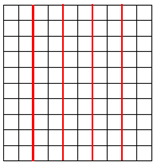
Otro procedimiento puede ser medir el lado del cuadrado sería: si el cuadro mide de lado 10 cm (o 10 cuadritos), haces la división para obtener 5 partes iguales, 10 entre 5 y el resultado es 2 es decir, que cada parte debe medir 2 cm (o 2 cuadritos). Ya obteniendo esto, puedes resaltar cada división con un color. Como se muestra en la imagen.
Cada parte corresponde a 1/5 que se lee “quinto” o “quinta parte”.
Con el mismo procedimiento anterior, obtén los décimos, 10 entre 10 = 1 cada parte debe medir 1 cm (o un cuadrito).
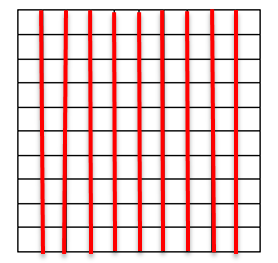
Como puedes ver, 10 cuadritos es el equivalente a 1/10 que se lee “décimo” o “décima parte”.
Tanto los quintos y los décimos cubren a la unidad, entonces ¿Cuáles serían algunas fracciones equivalentes?
Para obtener algunas fracciones equivalentes, realiza lo siguiente:
En el cuadrado de quintos, vas a colorear con amarillo los decimos que cubran la superficie de 1/5
Para obtener la fracción equivalente de 1/2 en décimos, toma el cuadrado de décimos y pinta de verde la parte que cubre la mitad de la superficie.
Resuelve las siguientes situaciones para practicar lo que has aprendido.
Compara las siguientes fracciones. Utiliza los símbolos, igual, = mayor que, > y menor que, <
¿Qué es menor 5/10 o 3/4?
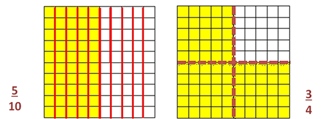
5/10 es menor que 3/4, porque solo cubre la mitad o 1/2 de la unidad.
Se puede representar como 5/10 < 3/4 y se lee “cinco décimos menor que tres cuartos”
¿Qué es mayor 2/3 o 4/6?
Para responder esta pregunta analiza el siguiente cuadrado de 12 cm (o 12 cuadritos de lado). Está dividido en tres partes iguales (que están remarcadas con rojo) y están coloreados 2/3 de amarillo. También está dividido en seis partes con la línea azul y así puedes observar qué parte ocupan 4/6
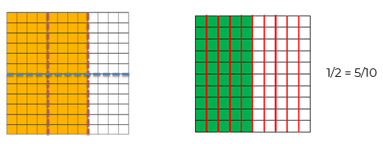
Como ves, 2/3 es igual a 4/6 ya a que ambos son equivalentes porque representan la misma cantidad de superficie iluminada.
Se puede representar como 2/3 = 4/6 y se lee “dos tercios es igual a cuatro sextos”.
¿Qué es mayor 4/6 o 5/10?
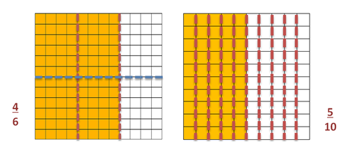
4/6 es mayor que 1/2 y 5/10=1/2 por lo tanto 4/6 es mayor que 5/10
Se puede representar como 4/6 > 5/10 y se lee “cuatro sextos mayor que cinco décimos”.
¿Qué fracción será menor 3/2 o 15/5?
Para contestar esta pregunta observa que en ambas fracciones el numerador es mayor que el denominador, es decir que estas fracciones son mayores a la unidad.
Observa la siguiente imagen:

La fracción 3/2 es una unidad más un medio, y se lee “tres medios es igual a un entero con un medio”.
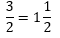
Para analizar la fracción 15/5, recuerda que una unidad se forma al unir 5/5, por lo que con 15/5 obtienes tres enteros, porque puedes unir tres veces 5/5 es decir 15/5= 3 y se lee “quince quintos es igual a tres enteros”.
Entonces 3/2 es menor que 15/5 y se puede representar como 3/2 < 15/5 o 1 ½ < 3
Sigue practicando para obtener más fracciones equivalentes, usa los cuadrados unidad para que las compares y sepas cuál es mayor o menor o si son iguales.
Recuerda que si tienes alguna duda tu maestro te la resolverá y seguramente te proporcionará más información que te permitirá saber más sobre el tema.
El Reto de Hoy:
Realiza la siguiente actividad.
Busca tres formas de comparar 2/6 con 3/9
Platica con tu familia sobre lo que aprendiste, seguro les parecerá interesante y podrán decirte algo más.
Descarga tu clase dando clic aquí
¡Buen trabajo!
Gracias por tu esfuerzo.


Login to join the discussion