La fábrica de fracciones

Aprendizaje esperado: r esolución de problemas que impliquen participaciones en tercios, quintos y sextos. Análisis de escrituras aditivas equivalentes y de fracciones mayores o menores que la unidad.

Énfasis : c omparar fracciones que se representan gráficamente, al dividir una unidad con ciertas condiciones.

¿Qué vamos a aprender?

Fortalecerás tus conocimientos de cómo comp a rar fracciones que se representan gráficamente, al dividir una unidad con ciertas condiciones.

¿Qué hacemos?

Recuerda que, si divides un objeto o unidad en varias partes iguales, a cada una de ellas se les conoce como fracción. Las que están formadas por el “denominador” que representa un divisor (o las partes en que se divide la unidad), y el “numerador”, que representa a un dividendo (o las partes que se toman luego de dividirse la unidad).

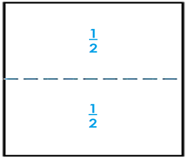
Si un en t ero lo divides a la mitad, en dos partes iguales, cada parte obtenida se ll a ma 1/2 y se lee medio o mitad.

Si un entero lo divides en cuatro partes iguales , cada parte obtenida se llama 1/4 y se lee cuarto o cuarta parte.

Si un entero lo divides en ocho partes iguales cada parte que obtienes se llama 1/8 y se lee octavo u octava parte.

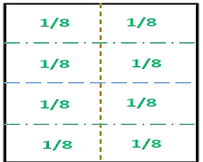
Viste que entre estas fracciones puedes identificar fracciones equivalentes, por ejemplo, un medio es equivalente a 2/4 y también 1/2 es equivalente a 4/8 .

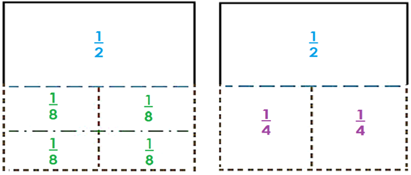
¿Recuerdas qué significa que una fracción sea equivalente a otra ?

S ignifica que una de las partes en que está dividido un entro, puede ser representada con fracciones de distinto tamaño, lo que implicaría también una escritura distinta.

Así, por ejemplo 2/8 son equivalentes a 1/4 o viceversa 1/4 es equivalente a 2/8

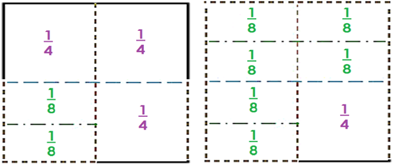
Revisa otras maneras en las que viste que un entero puede dividirse y las fracciones que pueden obtenerse de esa división.

Es importante recordar a nuestros alumnos y alumnas que una unidad o entero puede dividirse en las partes que se decida, pero siempre debes cuidar que sean del mismo tamaño, tanto al marcarlas como al recortarlas si es que así lo requieres.

Como ejemplo, puedes ver cómo al dividir un entero en tres partes iguales obtienes tercios:

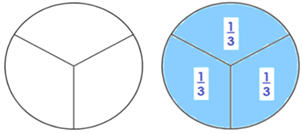
Si cada tercio lo divides en dos partes obtienes seis fracciones iguales, y cada una recibe el nombre de sexto o sexta parte.

Por último, recuerda que un noveno o novena parte se escribe como 1/9 y se obtiene al dividir un entero o unidad en nueve partes iguales.

A sí como viste en los cuadr ad os, también en los círculos puedes ver que los repartos de tercios, sextos y novenos cubren a la unidad, y puedes identificar en los círculos fracciones equivalentes cómo lo hiciste con los cuadrados. Por ejemplo; 1/2 es equivalente a 3/6 .

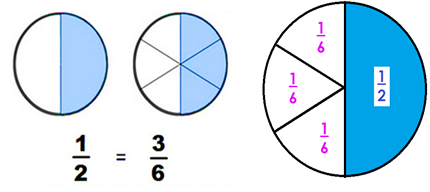
O bien, puedes establecer que un 1/3 = 3/9

Ahora realizarás algunas comparaciones entre las fracciones que has revisado.

¿Qué es mayor 1/2 o 3/4 ?

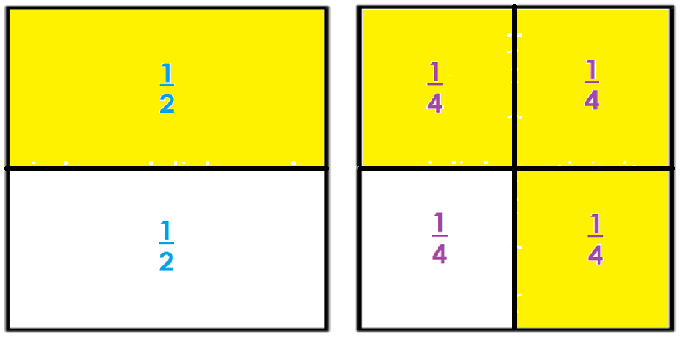
3/4 porque casi cubre la unidad.

Bien. Esta relación la puedes representar como:

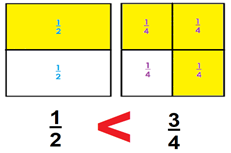
1/2 < 3/4 , y se lee un medio es menor que tres cuartos.

En color rojo destacamos el símbolo “menor que”, que junto con el símbolo “mayor que” te permite indicar la relación matemática que existe entre dos valores, en este caso fraccionarios. La parte abierta indica el valor mayor y el vértice el valor menor. Complementariamente el símbolo “=” te permite indicar que las cantidades existentes a ambos lados representan el mismo valor.

Ve a otro ejemplo:

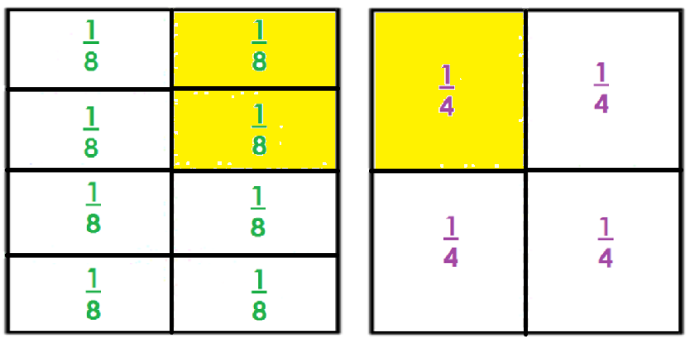
Pues ninguna fracción es menor, porque ambos son equivalentes o iguales.

Y lo puedes representar entonces como 2/8 = 1/4

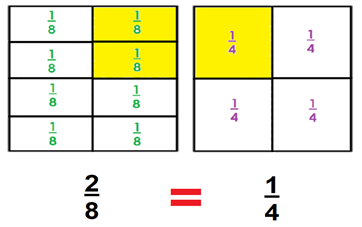
En la siguiente imagen .

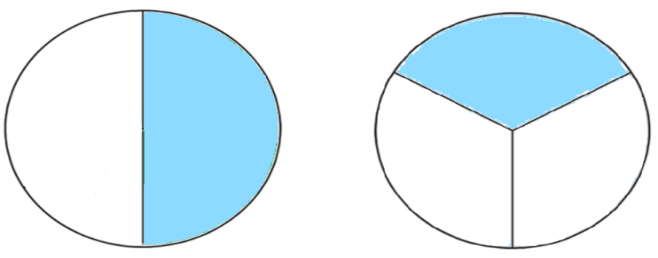
1/2 porque es media unidad y un tercio no cubre media unidad. Y lo puedes representar como 1/2 > 1/ 3, y se lee un medio es mayor que un tercio.

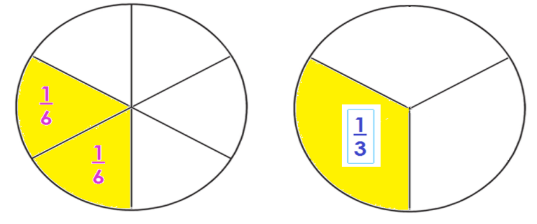
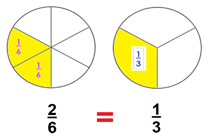
Ambos son equivalentes o iguales y lo puedes representar entonces como 2/6 = 1/3

Ahora .

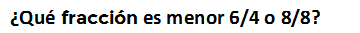
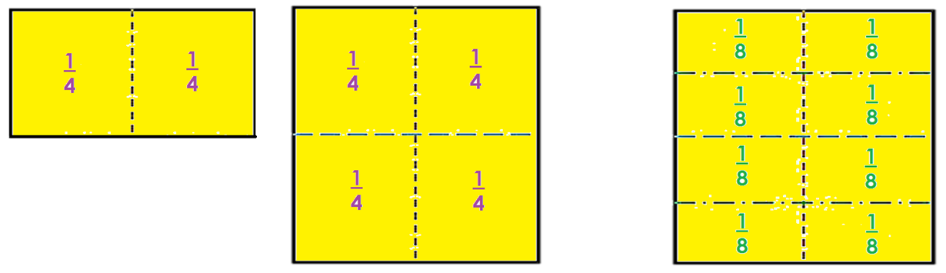
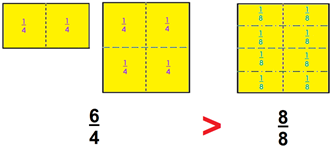
Este ejemplo nos permite tomar la primera fracción, 6/4 para ejemplificar una fracción impropia en la que el numerador es mayor que el denominador. Es decir, esta fracción es mayor a la unidad.

Entonces la fracción menor sería 8/8 porque 8/8 es igual a una unidad, 6/4 es más que una unidad.

Y la puedes representar como 6/4 > 8/8

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/20/P4DMA.htm

Descarga tu clase dando clic aquí